难熔元素合金化NiAl合金的第一性原理计算

卢彩彬，李新梅

(新疆大学机械工程学院，乌鲁木齐 830047)

NiAl合金作为一种航空高温结构材料，具有强度高、熔点高、化学成分变化范围广、耐腐蚀性好等物理性能，在航空航天领域有着广泛的应用前景，然而，NiAl 在室温下表现为脆性，其可塑性较差，低温塑性差和脆性晶界断裂限制了其实际的应用价值，合金化作为提高材料性能的一种有效方法，也是用来改善NiAl合金质量的一种有效方法[1-3]。因此，合金化作为提高NiAl金属间化合物的室温塑性的重要方法之一，并且已在NiAl、FeAl、TiAl等一系列金属间化合物的研究中取得了一定的成果。

Zhang等[4]通过添加活性元素Dy，研究发现Dy能显著改善NiAl合金的循环氧化；陈律等[5]发现随着Mo 的加入，共晶碳化物组织发生细化，其孤立化程度显著，这对提高合金的韧性十分有利。然而，这些原子级的机制不能通过原位实验直接探测，因而采用第一性原理计算方法可研究化学计量NiAl、富Ni和富Al NiAl中Dy的杂质形成能和溶解能,计算表明，Dy在3种NiAl中都能很容易地溶解在Al空位中。胡雪兰等[6]应用第一性原的方法和VASP软件研究了NiAl金属间化合物的P元素对其结构和力学性能的影响，研究发现P原子更易于占据Al替代位，P的加入使NiAl金属间化合物的局域塑性减小，脆性增加。He等[7]利用密度泛函理论(density functional theory，DFT)研究了稀土元素Pr、Pm、Sm和Eu对NiAl合金的结构、弹性和电学性能的影响，研究表明，Pr、Pm、Sm和Eu都倾向于替代Al原子，均可提高NiAl合金的塑性，并且Pm的加入使NiAl具有最大的塑性，加入 Eu元素可使硬度和塑性同时得到提高。

以上研究表明第一性原理在NiAl金属间化合物方面的计算应用具有可靠性，同时，由于材料的力学性能(如脆性/延展性、硬度/强度)源自材料的本征力学性质(如弹性模量与体模量等),而这些弹性常数的测试往往因材料本身缺陷和测试设备精度的问题而难以准确测定，因此，基于第一原理的量子力学计算具有无可替代的优势[8]。

目前，对NiAl合金的研究虽然较多，但随着多元合金化的发展以及实验条件的限制，探究合金元素对NiAl合金组织和性能的影响仍然非常重要，对NiAl合金塑韧性的改善以及其本征属性的研究还有待进一步的发现。

综上所述，合金化作为改善NiAl合金性能的有效方法，但通过实验方法研究需要大量的工作，而从晶胞及其电子结构方面研究合金化改善金属间化合物的性能可以节约许多不必要的消耗。因此，在第一性原理计算的基础上，旨在研究NiAl结构反位缺陷下合金元素Zr、Hf、Nb、Ta对其电子结构、力学性能及热力学性能的影响，现从最本质的微观电子结构出发，揭示合金元素对金属间化合物性能的影响，为研究NiAl金属间化合物的广泛应用具有重要的理论指导和实际价值。

1 计算方法与模型

1.1 晶胞模型的建立

NiAl 的晶体结构为有序的B2型体心立方结构，空间群为PM-3M,Al原子占据晶胞的8个顶点位置，即Al原子坐标为(0,0,0)；Ni原子位居晶胞的体心，原子坐标为(1/2,1/2,1/2)，NiAl的晶格常数为a=b=c=2.887 Å，α=β=γ=90°[9]。由于掺杂元素的量很少，所以建立的模型采取超胞结构，通过选取8个单胞构成的超胞来反映加入少量合金元素的实际问题。

因原子的热运动或成分偏离化学计量比时均会引起NiAl中的“组分点缺陷”，由于间隙原子的形成需要克服较高的能量势垒,一般可以忽略间隙原子的作用。因此空位与反位缺陷就成为金属间化合物中的主要点缺陷形式[10]。陈律等[11]通过研究发现B2-YX(X=Cu,Rh,Ag,In)4种金属间化合物内部存在的点缺陷对其塑性的提高起着积极的作用；同时早期研究[12]发现 NiAl合金在偏离化学计量比的情况下所呈现出来的点缺陷结构主要为Ni反位和Ni空位。主要研究反位缺陷，即Ni8Al8超胞在亚晶格位上有一个单点反位缺陷(NiAl或AlNi)或添加三元合金元素，如图1所示，其中M是添加的三元合金元素。

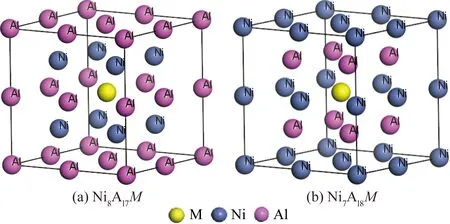
图1 NiAl 2×2×2计算模型Fig.1 NiAl 2×2×2 calculation model

在CASTEP(Cambridge serial total energy package)模块下构建包含16个原子的三维超晶胞晶体模型，超晶胞模型为Ni8Al8。在Materials Studio软件系统下采用基于DFT的第一性原理计算，赝势采用超软赝势，交换关联函数采用广义梯度近似[13](the generalized gradient approxi-mation,GGA)。

1.2 参数优化

几何结构优化的各个参数设置，通过结构优化对计算参数的可靠性进行测试，包括赝势、平面波截断能、布里渊区空间网格点以及交换关联泛函等参数。在CASTEP程序下采用BFGS方法(Broyden-Flecher-Goldfarb-Shanno)对超胞进行超高精度几何优化，精度为ultra-fine。布里渊区网格K点设置为4×4×4,6×6×6,8×8×8,10×10×10,12×12×12,14×14×14，16×16×16，18×18×18，平面波截断能Ecut-off为340～520 eV，截断能梯度为20 eV，对以上K点和截断能进行优化计算。其计算收敛标准如表1所示。

通过截断能及K点网格数的优化计算，得到当截断能Ecut=440 eV，网格数K=14×14×14时，晶胞能量趋于稳定且晶胞常数值最接近于实验值2.887 Å[14]。通过与实验对比验证，计算对比了反位缺陷下两种结构的晶胞参数具有可靠性，计算值与实验值吻合。

由以上计算证明参数设置准确。因此，在超胞Ni8Al8模型基础上进行性能计算。Al8Ni8结构优化前晶胞参数为5.774 Å，晶胞体积为192.5 Å3；在截断能E=440 eV，K=14×14×14下计算得Ni8Al8两种结构下参数如表3所示。

表1 计算收敛参数Table 1 The values of convergence parameters

表2 反位缺陷下两种结构的晶胞参数Table 2 Cell parameters of the two structures under the antiposition defect

表3 超胞模型参数Table 3 The parameters of supercell model

计算的结果和先前的理论计算值以及实验值都很符合，这也表明了理论计算的可靠性。

1.3 合金相占位稳定性计算

在以上模型建立及参数优化基础上，对加入的合金元素进行占位和能量稳定性计算，得到合金化元素在Ni8Al8超胞中的择优占位能，确定合金元素在超胞模型中的位置，以便于后续性能的计算分析。

通过比较合金元素原子替代NiAl合金中不同元素原子时体系的形成能可以得到合金元素原子倾向于合金的位置，这个差值被定义为择优占据能。

择优占位能[17]Esite计算公式为

Esite=E1-E2

(1)

E1=ENix-1AlxM-(x-1)ENi-xEAl-EM

(2)

E2=ENixAlx-1M-xENi-(x-1)EAl-EM

(3)

Esite=E1-E2=ENix-1AlxM-ENixAlx-1M+ENi-EAl

(4)

式中：x为Ni8Al8超胞中Ni原子或Al原子的原子个数；E1和E2分别为稀土元素优先占据Ni位和Al位的生成焓；ENi、EAl和EM分别为纯Ni、纯Al和纯合金化元素M的总能量。

当Esite<0时，合金元素更倾向于替代Ni原子，当Esite>0时，合金元素倾向于替代Al原子。

针对面心立方结构Ni晶胞和Al晶胞，对Ni3d84s2、Al3s23p1进行伪原子计算。计算得Zr、Hf、Nb和Ta的占位情况如表4所示。

表4 合金元素的占位计算Table 4 Calculation of alloying element occupancy

由表4可知，元素 Zr、Hf、Nb、Ta在晶胞中均优先于替代Al位，经对比实验值，计算结果同实验测量值相符合。

2 结果与分析

2.1 晶格常数

作为晶体物质的基本结构参数，晶格常数紧密相关于原子间结合能，反映晶体受力状态及内部成分变化[18]。计算对比了原合金结构的实验值及Zr、Hf、Nb、Ta合金化后合金相的晶格常数变化，如表5和图2所示。

由图2可知，由于加入合金化元素的原子半径不同，合金化后晶胞的晶格常数和体积也会发生变化，三类合金化结构的晶格常数与体积变化趋势均一致。相对于原Ni8Al8晶胞，在反位缺陷结构AlM下，合金化后晶胞的晶格参数均增加到不同程度，晶胞体积也增大，意味着晶胞膨胀。Ni8Al7Zr在平衡晶格常数和体积上表现出最大的变化。

表5 稳定结构下的合金相的平衡晶格常数Table 5 Equilibrium lattice constants of alloy phase under stable structure

图2 合金化结构晶胞常数与体积的变化图Fig.2 Changes in cell constant and volume of alloying structure

2.2 态密度

电子结构的差异是晶格稳定性差异的根本原因，用态密度来表征合金相的电子结构性能，态密度即E+dE这个能量范围内的能级数，当E+dE这个能量范围内轨道(能级数)越多越密集，态的密度越大[19]。当能带的所有能级都处于E+dE这个能量区间时，态的密度最大，在态密度图中表现为一个很尖锐的峰，反之，若能带的带宽较大，意味着态密度图很平缓，并且跨过的能量区间越大[20]。总之，能带图越平缓，态密度峰越尖锐，能带图越宽，态密度越平缓，离域性越强。

由图3和图4可以看出，Ni8Al7Zr的电子态密度位于-5～0 eV能量范围内的电子态密度存在最强峰，且主要由Ni原子的3d轨道贡献，Zr原子的p、d轨道和Al原子的s、p轨道也有相对较小的贡献；在-10～-5 eV能量范围内的电子态密度由Al原子的s、p轨道电子和Ni原子的s、p、d轨道电子构成；在能量范围较宽的0～20 eV内由Al的s、p轨道，Zr的p、d轨道和Ni的s、p、d轨道杂化构成，在整个能量区间内DOS分布较为平均，没有局域尖峰的DOS，对应的是类sp带，表明电子的非局域化性质很强。

图3 合金化后晶体的电子态密度图Fig.3 Electron density of states diagram of alloyed crystal

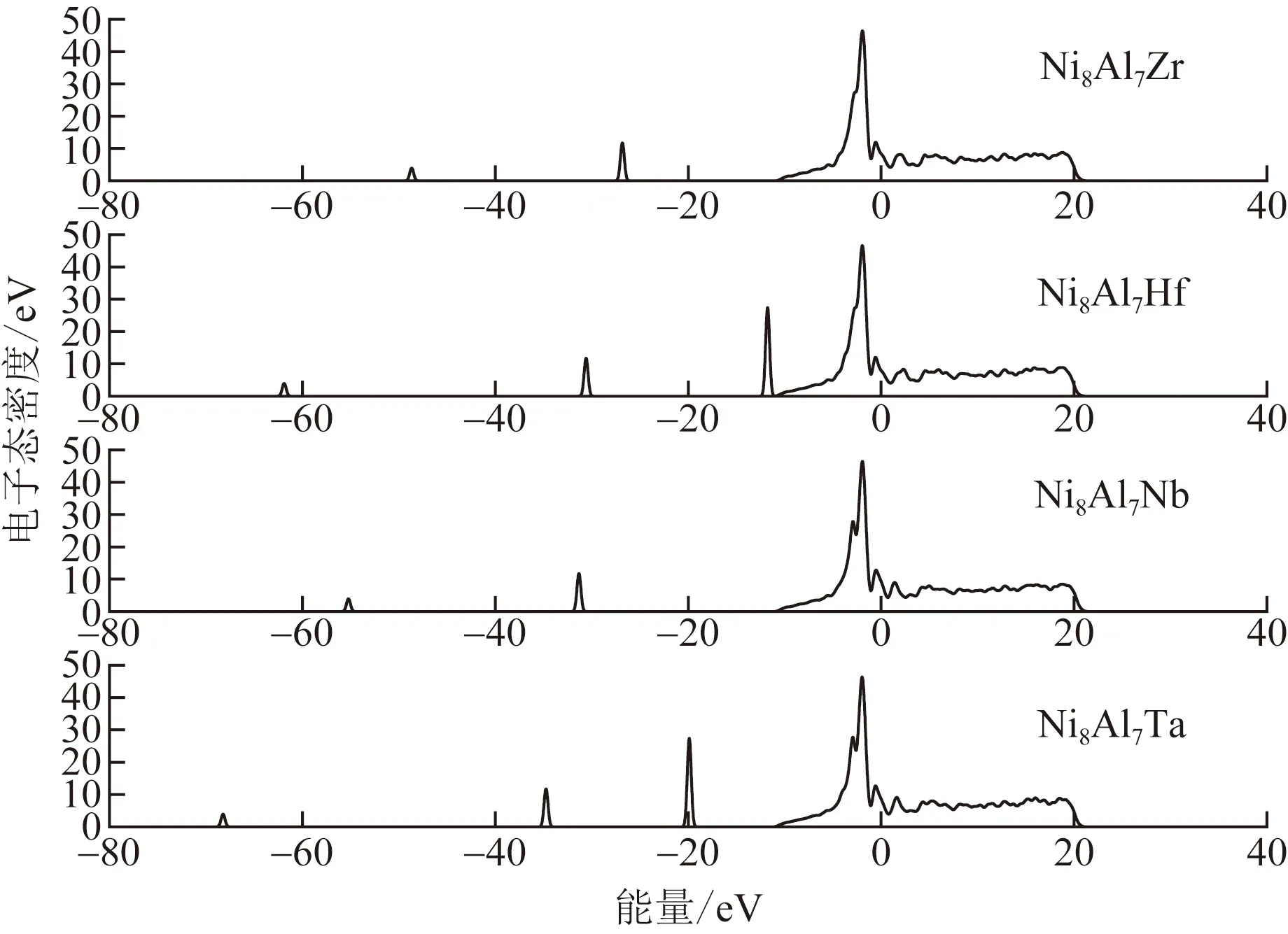
图4 合金相的总态密度图Fig.4 Total density of states of the alloy phase

Ni8Al7Hf的电子态密度在-5～0 eV能量范围内和能量为-12 eV附近出现大的尖峰，分别由Ni原子的3d轨道和Al原子的s、p轨道贡献最尖峰，且由于Hf原子的核外电子4f轨道达电子全满状态，电子的态密度贡献较大，因而提供了Ni8Al7Hf在能量为-12 eV和-30 eV 附近处较强的局域态密度尖峰；而在0～20 eV能量范围内的总的电子态密度分布较为平均，没有局域的DOS尖峰，态密度主要来自Al原子的s、p轨道电子和Ni原子的s、p、d轨道电子杂化构成。

Ni8Al7Nb的电子态密度在-10～0 eV能量范围内出现大的尖峰，主要由Ni原子的3d轨道、Al原子的s、p轨道贡献和Nb原子d轨道的弱贡献形成最尖峰，同时，在能量为-32 eV附近也出现较小的尖峰，态密度贡献完全来自合金元素Nb的d轨道电子；而在0～20 eV能量范围内的总的电子态密度分布较为平均，没有局域的DOS尖峰，对应能带的类sp带，电子的非局域化性质很强，态密度由Al原子的s、p轨道电子，Ni原子的s、p、d轨道电子和Nb原子的p、d轨道电子杂化而来。

Ni8Al7Ta的电子态密度同样在-5～0 eV能量范围内出现最强的尖峰，在-20 eV和-35 eV能量附近出现两个尖峰，最大的尖峰分别由Ni原子的3d轨道和Al原子的s、p轨道贡献，能量为-20 eV和能量为-35 eV附近的态密度贡献都来自合金化元素Ta的f轨道电子；在0～20 eV能量范围内的总的电子态密度同样分布较为均匀，没有出现局域的DOS尖峰，电子的非局域化性质很强，态密度主要来自Al原子的s、p轨道电子和Ni原子的s、p、d轨道电子杂化构成。

2.3 韧脆性分析

材料的韧/脆性可以通过材料的模量比(G/B)比值判断，即剪切模量G与体模量B的比值。Pugh的经验判据[21]指出，金属的塑性与其G/B有关，G/B值可以表征材料塑性变形的阻力，当G/B<0.57时，为韧性材料，具有良好的延展性和韧性，G/B值越小，材料韧性越好，G/B值越大，材料越脆。

除此之外，柯西压力值(C12-C44)也被用来表征材料的韧脆性，通过描述金属及化合物中原子键的特征，即金属键的存在会使柯西压力值增大，共价键因其具有方向性而会使柯西压力值减小，柯西压力值越小，共价键的方向性越强，脆性越大，且一般延性材料的柯西压力值为正，脆性材料为负，较小的负柯西压力表示相对韧性材料[22]。因而通过计算剪切模量与体模量的比值G/B的值和柯西压力值(C12-C44)来衡量NiAl合金及其合金化的韧脆性。

由图5(a)可知，相对于NiAl超胞结构，Zr、Hf、Nb、Ta等合金元素的加入均使柯西压力值不同程度地增大，表明合金元素的加入改善了NiAl合金的韧性；同时，从图5(b)可知，合金相G/B的值均小于0.57且相比于原晶胞结构出现不同程度的降低，合金相均呈现出相对韧性。

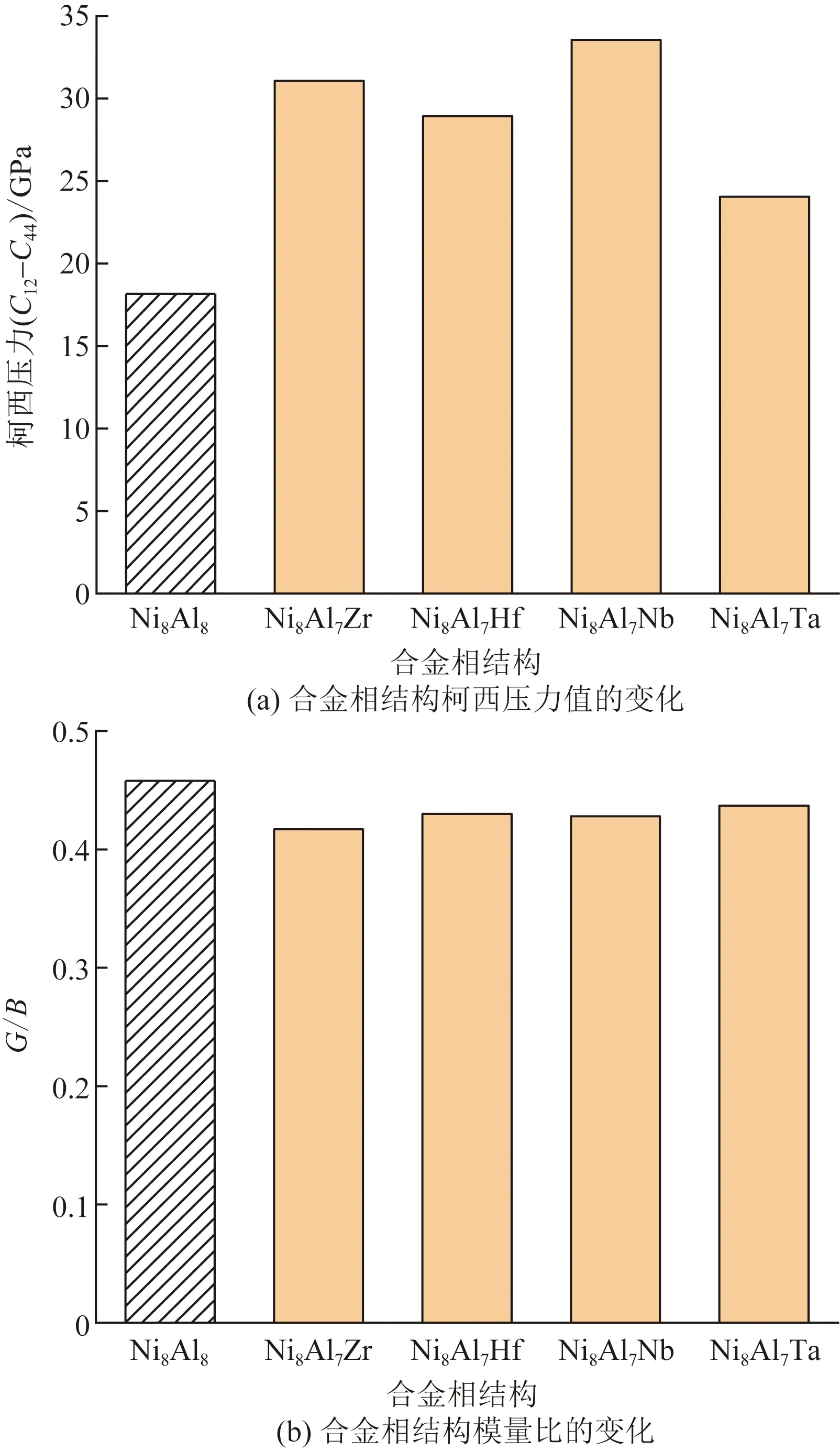
图5 合金相结构的柯西压力与G/B变化图Fig.5 Cauchy pressure and G/B changes of alloy phase structure

2.4 热学性能分析

为了解NiAl合金及其合金化后晶体结构的热力学性质，通过对合金相声子计算的基础上，利用准谐德拜模型计算了合金化后Ni8Al7Zr、Ni8Al7Hf、Ni8Al7Nb和Ni8Al7Ta等晶体的焓、熵、自由能、德拜温度以及热容随温度的变化曲线，如图6所示。

图6 合金相结构的焓、自由能和熵随温度的变化图Fig.6 Changes in enthalpy,free energy and entropy of alloy phase with temperature

由图6可知，随着温度的增加，4种晶体结构的熵随之一致增大；因为随温度的升高，晶体中的热运动增加，粒子的动能随之变大，晶体内能也变大，表明晶体内部粒子运动的无序程度也在增加[23]。根据焓的定义H=U+PV[24](其中H为焓，U为系统内能，P为压强，V为体积)，因为热力学能、焓是温度的函数，因而，当温度增加时，4种晶体体系的焓H也随之增加；同理，根据Gibbs自由能(G=H-TS)(其中G为Gibbs自由能，H为焓，T为温度，S为熵)的表述，合金相体系中熵随温度的增加趋势大于焓H随温度的变化，所以自由能随温度的升高而降低。

德拜温度是衡量晶体材料热学性能的重要物理量，可用来反映原子间的结合力，较高的德拜温度通常意味着室温下材料具有更好的热传导率[25]。利用德拜模型可以表征材料的热力学性质，为此计算了在0～1 700 K 温度范围内合金的德拜温度和热容，以预测高温下合金相的热稳定性能，计算结果如图7所示，当温度远低于德拜温度(即当温度小于20 K)和当温度处于35～400 K时，德拜温度的变化遵循量子规律，与温度的3次方成正比，符合德拜模型的T3定律，即德拜温度随温度的升高而增大，当温度为20～35 K时，德拜温度随温度升高而下降，而当温度大于400 K时，德拜温度逐渐趋近于稳定值420 K。同理，如图8所示，随着温度的升高当温度小于约400 K时，由于晶格热振动能量对晶体的热容也有贡献，因而热容随温度的升高增加明显，而随着温度升高，当温度大于400 K时，电子热运动能量对热容的影响逐渐忽略不计[26]，因而合金相的热容值均逐渐趋近于杜隆-珀替极限值，说明本文德拜模型的计算结果是合理的。

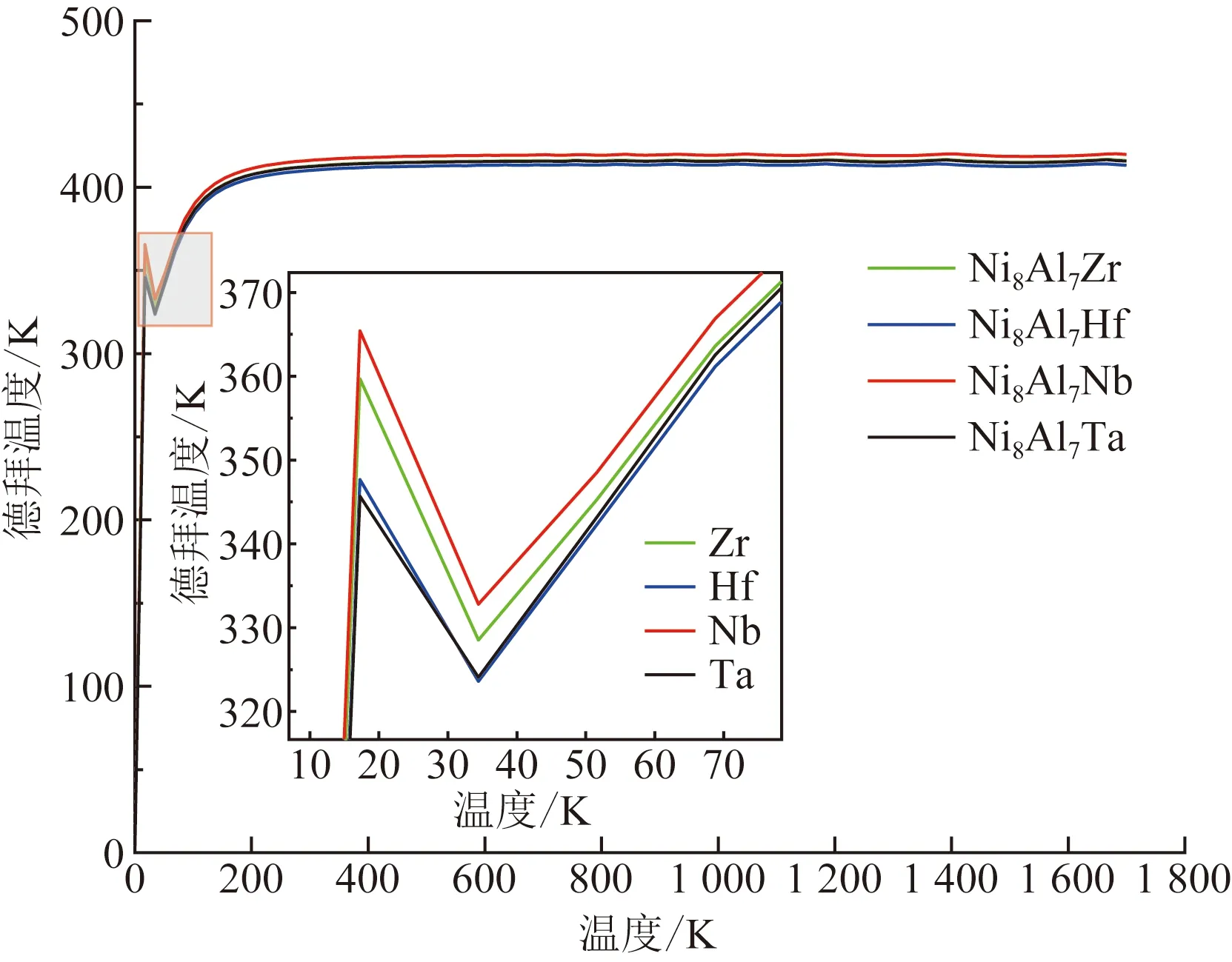
图7 合金化结构的德拜温度变化图Fig.7 Debye temperature variation diagram of alloy phase

图8 合金相的热容变化图Fig.8 Heat capacity changes of alloy phase

3 结论

在第一性原理理论方法基础上，通过计算合金化元素加入前后对NiAl合金的影响，计算了NiAl-M三元系合金相中第三相合金元素Zr、Hf、Nb、Ta在晶胞中的择优占位，并分析了合金相的晶胞参数、态密度、韧脆性及热学性能。

(1)经计算并与实验结果可得，Zr、Hf、Nb、Ta在晶胞中均优先于替代Al位，态密度图显示0～20 eV能量范围内，态密度分布均较为平均，没有局域的DOS尖峰，且Zr、Nb合金化相的态密度均主要由Al原子的s、p轨道电子和Ni原子的s、p、d轨道电子和Zr原子微弱的p、d轨道电子杂化构成，Hf、Ta合金化后相的态密度均主要由Al原子的s、p轨道电子和Ni原子的s、p、d轨道电子杂化构成；-10～0 eV能量区间内态密度均出现最强峰，且Zr、Nb的d轨道电子对态密度峰有贡献，Hf、Ta在-10～0 eV能量区间内无电子态密度分布。

(2)由柯西压力值判断，Zr、Hf、Nb、Ta的加入均使柯西压力值增大，且合金相G/B的值均小于0.57，合金相表现出相对韧性。

(3)在0～1 700 K温度范围内，合金相的焓、熵均随温度的升高而增大，自由能随之下降，当温度高于400 K时，合金相的德拜温度均趋于420 K；随温度的升高，合金相的热容值均趋近于杜隆-珀蒂极限值，同时表明本文的计算模型及其相应的计算结果是合理的。