奇数的拆分循环及应用
2021-09-26吴金钗
吴金钗
(华侨大学 数学科学学院, 福建 泉州 362021)
Mersenne数Mp=2p-1是以2为底的幂再减1的数[1-4],Fermat数Fn=22n+1是以2为底的幂再加1的数[4-9].在Mersenne数的分解方面,Cambraia[10]给出了方程Mm+Mn=2pa的整数解(m,n,a),其中,m,n≥2,p是一个质数,a是一个正整数.目前,国内外学者对于Fermat数分解算法研究的不多,国外有专门的网站介绍分解Fermat数的进展[10-12].Wang[13]提出分解Fermat数的新方法,理论上可分解Fn(n>100 001)的任何Fermat数.王钰[14]对Wang[13]的方法进行优化,运用Maple数学软件解析Fermat数小因数,优化后的算法提高了计算效率.然而,Wang[13]利用GMP大数库运算在32位系统中只能计算到F22,王钰[14]利用Maple在64 位系统中也只能计算到F29.因此,研究更通用、更高效的大数算法是很有必要的.基于此,本文提出奇数的拆分循环及其应用.
1 奇数的和式拆分循环
1.1 奇数的和式拆分

由于A是有限集合,所以∀α0∈A,∃αi∈A,不妨设i=1,2,…,k及数l1,l2,…,lk,使得p-αi-1=2liαi,α0=αk,拆分序列为
p-α0=2l1α1,p-α1=2l2α2, …,p-αk-1=2lkαk=2lkα0.
(1)

如果奇数p有两个拆分循环,且两个循环有一个相同的节点,则这两个循环的节点必完全相同,即这两个循环实质是同一个拆分循环,只是它们的起点不同.如果p有两个拆分循环(Ⅰ),(Ⅱ),则仅当拆分循环(Ⅰ)的节点与拆分循环(Ⅱ)的节点全不相同时,才称拆分循环(Ⅰ),拆分循环(Ⅱ)是p的两个不同的拆分循环.当p为素数时,则p与拆分循环的各节点的最大公因数(p,α0,α1,…,αk-1)=1;当p是合数时,如p=p1·p2(p1,p2为素数),则p与拆分循环的各节点的最大公因数(p,α0,α1…,αk-1)=1或p1或p2.
1.2 拆分循环结果
因为p-α0=2l1α1=2l1(p-2l2α2)=2l1p-2l1+l2α2=2l1p-2l1+l2(p-2l3α3)=(2l1-2l1+l2)p+2l1+l2+l3α3,所以当2j p·(2l1+l2+…+l2j-1-2l1+l2+…+l2j-2+…+2l1-1)=2l1+l2+…l2jα2j-α0; (2) 当2j-1 p·(2l1+l2+…+l2j-2-2l1+l2+…+l2j-3+…-2l1+1)=2l1+l2+…l2j-1α2j-1+α0. (3) 当k=2s时,α2s=α0,由拆分序列(1),有 p·(2l1+l2+…+l2s-1-2l1+l2+…+l2s-2+…+2l1-1)=α0(2l1+l2+…+l2s-1)=α0(2m-1). (4) 当k=2s-1时,α2s-1=α0,由拆分序列(1),有 p·(2l1+l2+…+l2s-2-2l1+l2+…+l2s-3+…-2l1+1)=α0(2l1+l2+…+l2s-1+1)=α0(2m+1), (5) 综上所述,当p的拆分循环为偶循环时,p|2m-1;当p的拆分循环为奇循环时,p|2m+1. L=nNn+(n-1)Nn-1+…+2N2+1·N1. 定理1设p=2a+1=2n+δn-12n-1+δn-22n-2+…+δn22+δ12+1,δi取1或0,i=1,2,…,n-1,则p的全体和式拆分的指数和为a,即L=nNn+(n-1)Nn-1+…+2N2+N1=a.因此,p是素数或合数,a是奇数或偶数,此结论均成立. 证明:将p改写为 p=2a+1=2l(2n-l+δn-12n-1-l+…+δl+12+δl2-1)+ [(1-δl)2l+δl-12l-1+…+δ12+1], 则右端第一项圆括号中的数和第二项的数都是奇数,所以和式拆分指数≥l的拆分节点为奇数,即1,3,5,…,2n-l+δn-12n-1-l+…+δl+12+δl2-1. 和式拆分指数≥l的拆分个数为 Nn+Nn-1+…+Nl=[(2n-l+δn-12n-1-l+…+δl+12-δl2-1)+1]÷2= 2n-1-l+δn-12n-2-l+…+δl+22+δl+1+δl, 因此, Nn+Nn-1+…+N1=2n-2+δn-12n-3+…+δ32+δ2+δ1, Nn+Nn-1+…+N2=2n-3+δn-12n-4+…+δ42+δ3+δ2, ⋮ Nn+Nn-1+Nn-2=2+δn-1+δn-2, Nn+Nn-1=1+δn-1, Nn=1, L=nNn+(n-1)Nn-1+…+2N2+1N=2n-1+δn-12n-2+…+δ12+1=a. 设p=α+2lβ是一个和式拆分,则α,β≤a,且2lβ>a.若1 因为Nn+Nn-1+…+Nk=2n-k-1+δn-12n-k-2+…+δk+22+δk+1+δk,Nn+Nn-1+…+Nk+1=2n-k-2+δn-12n-k-3+…+δk+32+δk+2+δk+1,所以Nk=2n-k-2+δn-12n-k-3+…+δk+32+δk+2+δk(k=1,2,…,n-2),而Nn=1,Nn-1=δn-1,Nn-2=1+δn-2,有 (6) 引理1对任意的n≥1,有 (7) 将式(7)代入式(6),全体超半拆分的指数和为 L1=2n-1-1+(2n-2+1)δn-1+(2n-3-1)δn-2+…+(22-1)δ3+(2-1)δ2= 2n-1+δn-12n-2+δn-22n-3+…+δ322+δ22+δ1-(1+δn-1+δn-2+…+δ2+δ1)= a-(1+δn-1+δn-2+…+δ1). 证明:对任意自然数n,有恒等式 成立. 再设bk=ak-ak-1,则bn=an-an-1=(n-1)+(n-3)+(n-4)·2+(n-5)·22+…+(k-1)2n-2-k+…+3·2n-6+2·2n-5+1·2n-4,bn-1=an-1-an-2=(n-2)+(n-4)+(n-5)·2+(n-6)·22+…+(k-1)2n-3-k+…+3·2n-7+2·2n-6+2n-5.所以有 bn-bn-1=1+1+2+22+…+2n-6+2n-5+2n-4=2n-3. 由数列an=2n-1-1,得a1=0. 例1求下列各数的所有和式拆分循环:a) 素数p=23;b) 素数p=43;c) 合数p=35. 43-1=2·21,43-21=2·11,43-11=25·1,由此奇循环导出43·(22-2+1)=27+1; 43-3=23·5,43-5=2·19,43-19=23·3,由此奇循环导出43·(24-23+1)=3·(27+1); 43-7=22·9,43-9=2·17,43-17=2·13,43-13=2·15,43-15=22·7,由此奇循环导出了43·(25-24+23-22+1)=7·(27+1). 其基循环为35-1=2·17,35-17=2·9,35-9=2·13,35-13=2·11,35-11=23·3,其偶循环为35-3=25·1,由此循环导出35·(27-24+23-22+2-1)=212-1;35-5=2·15,35-15=22·5,由此循环导出35·(2-1)=5·(23-1),35-7=22·7,35=7·(22+1). 因此,素数43有3个奇循环,且各循环的指数和都是7;而合数35有偶循环,也有奇循环,各循环的指数和也不一样. 例2用a)p=23;b)p=35的超半拆分,验证超半拆分指数和定理. a)p=2a+1=2·11+1=23=24+22+2+1,故a=11,δ1=1,δ2=1,δ3=0,a-(δ3+δ2+δ1+1)=8.23的超半拆分为23-13=2·5,23-15=23,23-17=2·3,23-19=22,23-21=2,这些超半拆分指数和是8. b)p=2a+1=2·17+1=35=25+2+1,所以a=17,δ4=0,δ3=0,δ2=0,δ1=1,a-(δ4+δ3+δ2+δ1+1)=17-2=15.35的超半拆分为35-19=24,35-21=2·7,35-23=22·3,35-25=2·5,35-27=23,35-29=2·3,35-31=22,35-33=21,超半拆分的指数和是15. 设p=2a+1=2n+δn-12n-1+δn-12n-2+…+δ12+1,令奇数集{1,3,5,…,p-2}为B,|B|=a,则∀α∈B,∃β∈B及数l(1≤l≤n+1),使得p=2lβ-α,其中,p为一个差式拆分,α为拆分的起点,β为拆分的接点,l为拆分的指数. 由于B是有限集,所以∀α0∈B,∃αi∈B及数li,1≤li≤2n(i=1,2,…,k),αk=α0,使得 p+α0=2l1α1,p+α1=2l2α2, …,p+αk-1=2lk·αk=2lkα0. (8) 式(8)中:拆分序列是一个以α0为起点的差式拆分循环. 由拆分序列(8)导出 p+α0=2l1(2l2α2-k)=2l1+l2(2l3α3-p)-2l1p=2l1+l2+l3(2l4α4-p)-2l1p-2l1+l2p=…= 2l1+l2+…+lkα0-2l1p-2l1+l2p-…-2l1+l2+…+lk-1p, 当l1>1时,由于 p+α0=2(2l1-1α1+α0), p+(2l1-1α1+α0)=2l1-1α1+2(2l1-1α1+α0)=2[(2l1-1+2l1-2)α1+α0], p+[(2l1-1+2l1-2)α1+α0]=2[(2l1-1+2l1-2+2l1-3)α1+α0]=…, p+[(2l1-1+2l1-2+…+2)α1+α0]=2[(2l1-1+2l1-2+…+2+1)α1+α0]= 2[(2l1-1)α1+α0]=2(p-α1)=21+l2α2, 由p-α0=2l1α1,p-α1=2l2α2导出l1个差式拆分序列,这个拆分序列前l1-1个的拆分指数为1,最后一个拆分的指数为l2+1.所以这个拆分的指数和为l1+l2.与这l1个拆分序列对应的节点序列起点是α0,最后的节点是α2. 同理可证,若p有一个和式拆分奇循环,即 例3求p=23的导出结果. p=23只有一个和式拆分偶循环,指数和为m=11.p=23的一个差式拆分循环为23+1=23·3,23+3=2·13,23+9=25·1,此循环导出的结果为23·(26+24+23+1)=1·(211-1).23的另一个差式拆分循环为23+5=22·7,23+7=2·15,23+15=2·19,23+19=2·21,23+21=22·11,23+11=2·17,23+17=23·5.此循环导出的结果为23·(28+27+25+24+23+22+1)=5·(211-1). 例4求p=43的导出结果. p=43的基循环43-1=2·21,43-21=2·11,43-11=25是一个指数和m=7的奇循环,此循环导出的结果为43·(22-2+1)=1·(27+1). 对应于此奇循环,43有一个差式拆分循环:43+1=22·11,43+11=2·27,43+27=2·35,43+35=2·39,43+39=2·41,43+41=22·21,43+21=26·1,此循环导出的结果为 43·(28+26+25+24+23+22+1)=22·7-1=214-1. 定理2素数p的任一偶循环的指数和都是奇数. 由反证法,设m为偶数,且m=2m1.因为p|2m-1=(2m1-1)(2m1+1),所以2m1≡1(modp)或2m1≡-1(modp).因m1 当k为奇数时,p|2l1+l2+…+lkαk+α0,即2m1+tαk+α0≡0(modp),因为2m1≡±1(modp),0 推论1设素数p有一个偶循环,指数和为m,则所有满足2r≡1(modp),minr=m. 证明:设(m,r)=m1,若m1=1,则m,r互素,因此∃P>0,Q>0,使得Pm-Qr=1,或Pr-Qm=1.因为2Pm=2Qr+1,或2Pr=2Qm+1,所以1≡2Pm≡2Qr+1≡2(modp)或1≡2Pr≡2Qm+1≡2(modp)不成立.若1 定理3素数p的基循环若是指数和为m的偶循环,则p的任一循环都是指数和为m的偶循环.素数p的基循环若是指数和为m的奇循环,则p的任一循环都是指数和为m的奇循环. 证明:若p只有一个拆分循环,定理结论自然成立.设p有一个异于基循环,指数和为m1的循环(Ⅰ),若循环(Ⅰ)是偶循环,则由定理2可断定m1|m,则基循环是偶循环,且p|2m1-1.由定理2可断定m|m1,因此,m1=m. 若循环(Ⅰ)是奇循环,则p|2m1+1,由定理2及推论1易证,m1是所有满足2r+1≡0(modp)r的最小值.若2r+1≡0(modp),则m1|r.如果p|2m1+1成立,则因为p|2m-1,p|2m+1不能同时成立,故m1≠m.若m 推论2如果素数p=2a+1有b个拆分循环,每个循环的指数和为m,那么,p的和式拆分的指数和a=bm(定理1),即p=2a+1=2bm+1. Mp=2p-1形的数为Mersenne数,其中,p为素数.当p=2,3,5,7,13,17,19,31,61,89,107,127,521,807,1 279,2 203,2 281时,Mp为素数[1].近代大型计算机偶然算出几个大数p的Mp是素数. 例5如果p=4m+3是素数,q=2p+1也是素数,则q|2p-1,Mp=2p-1是合数. 要证明M23=223-1有素因数p=2·23+1=47,设223-1=(2·23+1)(2·23·4b+1),则222-1=(211-1)(211+1)=2·232·4b+23·(1+4b).因为211=2 048,211-1=2 047=23·89,所以89· 2 049-1=4·47b,22·2 049+512=47b,令b=2b1,得47b1=11·2 049+256=22 795,求得b1=485,b=970,2·23·4b+1=8·23·970+1=178 481,即223-1=47·178 481. 例6设素数p=4n+1,q=2p+1 也是素数,则q|2p+1. 例7p为素数,且q=4p+1也是素数,则q|22p+1. 证明:设q的拆分循环指数和为m,m|2p,若m=p,q有两个拆分循环,两循环的节点个数之和必是偶数,而q的节点总个数为奇数2p/2=p,所以m≠p,m=2p.因为q只有一个指数和为2p的奇循环,所以q|22p+1.如p=3,q=4p+1=13,13|22p+1=26+1;p=13·q=4p+1=53,53|226+1. 例5说明p=4m+3是素数,q=2p+1是素数,则Mp必为合数.反之,若p=4m+3是素数,q=2p+1是合数,则Mp必为素数.如p=31,q=2p+1=63是合数,M31=231-1是素数;p=61,q=2p+1=123是合数,M61是素数;p=107,q=2p+1=215是合数,M107是素数;p=127,q=2p+1=215是合数,M127是素数;p=807,q=2p+1=2·807+1是合数,M807是素数;p=1 279,q=2p+1=2·1 279+2 559是合数,M1 279是素数;p=2 203,q=2p+1=2·2 203+1=4 407是合数,M2 203是素数. 例8p=19是素数,2p+1=39是合数,而M19=219-1是素数. 例9用拆分理论证明F5=225+1=232+1是合数. 证明:设F5=232+1=p·q,p=2a+1为F5的素因数,p的拆分循环为奇循环,指数和为25=32,25|a,p应当是形如2·25n+1的数.当n为奇数时,p有奇数个拆分奇循环,其总节点数应当是奇数,这与p=2·25n+1的节点总数24n个矛盾,故n应当是偶数. 设p=2·25·2a+1=27a+1,q=27b+1,即F5=232+1=(27a+1)(27b+1),则225=27ab+a+b,令a+b=27c,则218=ab+c=27ca-a2+c,即218+a2=(27a+1)c,将其变形为218a+a3=(27a+1)ca,218a+211-211+a3=(27a+1)ca,-211+a3=(27a+1)(ca-211),再变形为24+a4=(27a+1)(ca2-211a+24). 若ca2-211a+24=1,则24-1+a4=5·3+a4=27a.取a=5,则3+53=128=27,所以F5=225+1有一素因数p=27·5+1=641.再由ca2-211a+24=25c-2 048·5+16=1,求得c=409,b=27c-a=128·409-5=52 347,q=27b+1=128·52 347+1=6 700 417.1.3 拆分指数和

1.4 超半和式拆分及所有超半拆分的指数和



1.5 范例

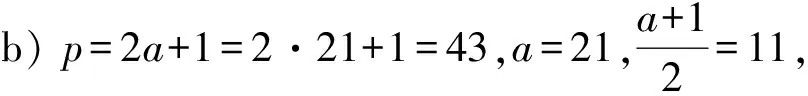
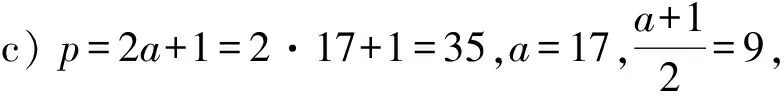
2 奇数的差式拆分循环
2.1 奇数的差式拆分

2.2 奇数p的差式拆分循环与和式拆分循环的关系
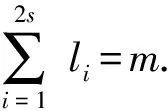
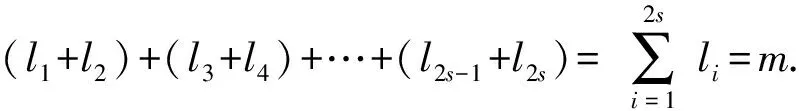
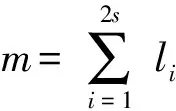

2.3 范例
3 素数和式拆分循环
3.1 素数的和式拆分
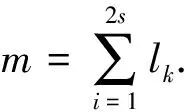
3.2 范例



