对象导出三支概念格的熵属性约简

吴荣， 张文娟， 李进金，

(1. 华侨大学 数学科学学院， 福建 泉州 362021； 2. 闽南师范大学 数学与统计学院， 福建 漳州 363000)

形式概念分析(format concept analysis，FCA)理论是德国数学家Wille[1]于1982年提出的，它是根据数据集中对象与属性的二元关系建立的一种概念层次结构，体现了概念之间的泛化和特化关系. 属性约简是其热点问题，自提出以来，深受众多学者的关注. Zhang等[2]设计了保持格结构不变的属性约简；Wang等[3]提出了保持交不可约元外延集不变的属性约简. 基于不可约元，Li等[4]进一步探讨了保持并不可约元外延集不变的属性约简；Wu等[5]将粒计算思想与形式概念分析相结合，探究了粒约简方法；Wei等[6]分别研究了两类协调决策形式背景的属性约简；Liu等[7]探讨了面向属性概念格与面向对象概念格上的属性约简.

2009年，Yao[8-10]提出了以“三分而治”为主要思想的三支决策理论，该理论的提出有着丰富的内涵. 而后，Qi等[11]将三支决策应用于形式概念分析理论，提出了三支形式概念，建立了三支概念格. 在此基础上，Qi等[12]进一步考虑了三支概念格与经典概念格的关系. 随后，Ren等[13]讨论了对象导出三支概念格和属性导出三支概念格的4种约简方法. 常欣欣等[14]和林洪等[15]分别从形式背景与决策形式背景出发研究了对象导出三支概念格的粒约简方法.

人们也利用信息熵[16]来研究形式背景的约简. 如Li等[17]、Singh等[18]利用信息熵计算形式概念的属性权重并进行概念格的属性约简. 李美争等[19]基于所有概念外延定义了形式背景的粗糙熵，提出了基于粗糙熵的属性重要度，并设计了相应的属性约简算法. 张鹤晓等[20]通过给出单个属性的信息量，研究了基于信息熵的对象加权概念格. 陈东晓等[21]从信息粒的角度出发，探讨了信息熵研究形式背景的一种方法.

虽然关于对象导出(object export，OE)三支概念格属性约简方法的研究已取得了很多成果，但与信息熵结合的研究较少.受文献[21]的启发，本文将信息熵引入形式背景中，探讨对象导出三支概念格的熵属性约简.

1 预备知识

定义1[22](U，AT，I)是形式背景，其中U是对象集，AT是属性集，I是U和AT的二元关系.对于任意x∈U，m∈AT，若(x，m)∈I，则表示对象x具有属性m.若(x，m)∉I，则表示对象x不具有属性m.

对任意的X⊆U，B∈AT，Wille定义了一对算子，即

X*={m∈AT|∀x∈X(xIm)}，

(1)

B*={x∈U|∀m∈B(xIm)}.

(2)

若满足X*=B和B*=X，则称(X，B)为(U，AT，I)的形式概念.其中，X和B分别称为概念的外延和内涵.记所有形式概念的集合为L(U，AT，I).

在形式背景(U，AT，I)中，任意B⊆AT，记IB=I∩(U×B)，那么(U，B，IB)也是一个形式背景， 称为子形式背景.且子形式背景(U，B，IB)中由式(1)和(2)定义的算子记为*B.

通过将三支决策思想引入形式概念分析中，Qi等[11]建立了三支概念格. 下面首先给出一些基本的定义.

设S是一个非空集合，P(S)是S的幂集，DP(S)=P(S)×P(S).在DP(S)上，定义集合间运算: 任意(A，B)，(C，D)∈DP(S)，(A，B)∩(C，D)=(A∩C，B∩D)，(A，B)∪(C，D)=(A∪C，B∪D)，(A，B)c=(Ac，Bc)，且有(A，B)⊆(C，D)⟺A⊆C且B⊆D.

相对于Wille定义的“*”算子，Qi等定义了如下算子，即

(3)

(4)

设(U，AT，I)是形式背景，对任意的X，Y⊆U，A，B⊆AT，对象导出三支算子< ·和>·具有以下4点性质:1)X⊆X< ·>·，(A，B)⊆(A，B)>· < ·；2)X⊆Y⟹X< ·⊇Y< ·，(A，B)⊆(C，D)⟹(A，B)>·⊇(C，D)>·； 3)X< ·=X< ·>· < ·，(A，B)>·=(A，B)>· < ·>·；4)X⊆(A，B)>·⟺(A，B)⊆X< ·.

在定义2中，若满足X< ·=(B，C)，(B，C)>·=X，则称(X，(B，C))为OE-概念.其中X称为OE-概念的外延，(B，C)称为OE-概念的内涵.

记所有OE-概念构成的集合为OEL(U，AT，I).对于任意(X，(B，C))，(Y，(D，E))∈OEL(U，AT，I)，OEL(U，AT，I)上二元关系:(X，(B，C))≤(Y，(D，E))⟺X⊆Y⟺(B，C)⊇(D，E).

对于任意(X，(B，C))，(Y，(D，E))∈OEL(U，AT，I)，则其上确界与下确界定义为

(X，(B，C))∨(Y，(D，E))=((X∪Y)< ·>·，(B，C)∩(D，E))，

(5)

(X，(B，C))∧(Y，(D，E))=(X∩Y，((B，C)∪(D，E))>· < ·).

(6)

因OEL(U，AT，I)中每个元素都是形式背景(U，AT，I)的对象导出三支概念，且(OEL(U，AT，I)，≤)是完备格，故称OEL(U，AT，I)为形式背景(U，AT，I)的对象导出三支概念格，简称OE-概念格.

2 对象导出三支概念格的熵属性约简

定义3设(U，AT，I)是一个形式背景，任意B⊆AT，记ΔB={x< ·B>·B，∀x∈U}，称ΔB为B诱导的关于U的覆盖.

命题1设(U，AT，I)是一个形式背景，如果B⊆AT，C=AT-B，则对于任意x∈U，x< ·AT>·AT=x< ·C>·C∩x< ·B>·B.

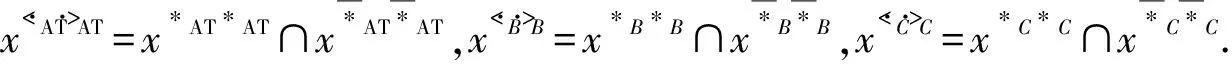
定义4假设(U，AT，I)是一个形式背景，定义关于对象导出三支概念格的信息熵为H(AT)=

定理1设(U，AT，I)是一个形式背景，对于C⊆B⊆AT及对象导出三支概念格的信息熵H(C)，H(B)，则有H(C)≤H(B).

定理2设(U，AT，I)是一个形式背景，C⊆B⊆AT， 若对象导出三支概念格的信息熵H(C)和H(B)，有H(B)=H(C)，则对任意x∈U，有x< ·B>·B=x< ·C>·C.

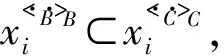
定理3设(U，AT，I)是一个形式背景，B，C⊆AT，若对于C⊆B及对象导出三支概念格的条件信息熵H(C|B)和H(B|C)，则有H(C|B)=0，H(B|C)=H(B)-H(C).

定理4设(U，AT，I)是一个形式背景，若对于C⊆B⊆AT及对象导出三支概念格的条件信息熵H(C|AT)和H(B|AT)，则有H(C|AT)≤H(B|AT).

证明: 由C⊆B可知，x< ·B>·B⊆x< ·C>·C，故有x< ·B>·B∩x< ·AT>·AT⊆x< ·C>·C∩x< ·AT>·AT， 即有H(C|AT)≤H(B|AT).

定理5假设(U，AT，I)是一个形式背景，对于B，C⊆AT，以及对象导出三支概念格的条件信息熵H(B|C)， 联合信息熵H(B:C)和信息熵H(C)，则有H(B|C)=H(B:C)-H(C).

证明: 由定义4可得.

定义5设(U，AT，I)是一个形式背景，对于B⊆AT及其对象导出三支概念格的信息熵H(B)，若满足H(B)=H(AT)，称B是对象导出三支概念格的熵协调集.若H(B)=H(AT)，且对任意C⊂B有H(C)≠H(AT)，则称B是对象导出三支概念格的熵约简集.

定理6假设(U，AT，I)是一个形式背景，任意a∈AT，a为非核心属性当且仅当H({a}|AT-{a})=0.

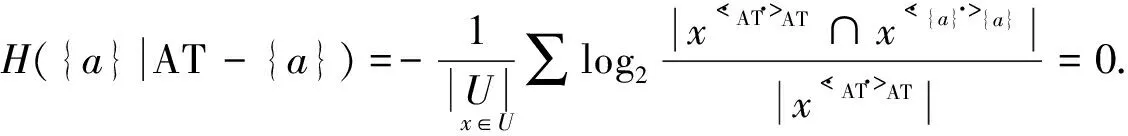
定理7设(U，AT，I)是一个形式背景， 对任意a∈AT，a为核心属性当且仅当H({a}|AT-{a})>0.

表1 形式背景(U，AT，I)Tab.1 Formal contexts (U，AT，I)

证明: 由定理6可知.

例1设(U，AT，I)是一个形式背景，其中，U={1，2，3，4，5}，AT={a，b，c，d，e}，如表1所示.

定理8设(U，AT，I)是一个形式背景，B⊆AT，若B是对象导出三支概念格的熵约简集，当且仅当其对象导出三支概念格的信息熵H(B)，有H(B)=H(AT)且对任意a∈B，H({a}|B-{a})>0.

证明: 因为B是对象导出三支概念格的熵约简集，则B是对象导出三支概念格的熵协调集，故而有H(B)=H(AT).而对任意a∈B，此时a是B中的核心属性，由定理7可知，H({a}|B-{a})>0.

反之，若H(B)=H(AT)，则B是对象导出三支概念格的熵协调集.若对于任意a∈B，有H({a}|B-{a})>0，则由定理7可知，a是B中的核心属性，也即任意a∈B，B-{a}均不是对象导出三支概念格的熵协调集，故B是对象导出三支概念格的熵约简集.

上述定理虽给出了对象导出三支概念格的核心属性与非核心属性的熵判定条件，并未给出区分相对必要属性与不必要属性的方法，但仍可获得对象导出三支概念格的熵约简集. 从核心属性出发，先判别核心属性集是否是约简集，若是则核心属性集为约简集；否则在此基础上依据定理8，逐次添加恰当属性直至获得约简集.

例2续例1，不妨取B={a，b，c}，通过计算可得H(B)=H(AT)，故B是对象导出三支概念格的熵协调集.因为b，c为核心属性，故H({b}|{a，c})>0，H({c}|{a，b})>0.又因为H({a}|{b，c})>0，从而a是B中的核心属性，也即B中每个元素都是必不可少的，故B为对象导出三支概念格的熵约简集.

定义6[14]设(U，AT，I)是一个形式背景，若存在B⊆AT使得对所有的x∈U均满足x< ·B>·B=x< ·AT>·AT，称B是OEG协调集.若B是OEG协调集而任意C⊂B均不是OEG协调集，则称B是OEG约简集.

定理9设(U，AT，I)是一个形式背景，B⊆AT，若B是OEG协调集当且仅当B是对象导出三支概念格的熵协调集，B是OEG约简集当且仅当B为对象导出三支概念格的熵约简集.

证明: 若B是OEG协调集，任意x∈U都有x< ·B>·B=x< ·AT>·AT，显然H(B)=H(AT)，故B是对象导出三支概念格的熵协调集.

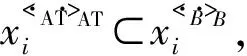
若B是OEG约简集，假设存在某个b0∈B，使得B-{b0}是对象导出三支概念格的熵协调集，则对任意x∈U，有x< ·AT>·AT=x< ·B-{b0}>·B-{b0}，从而B-{b0}是OEG协调集，这与B是OEG约简集矛盾，故而B是对象导出三支概念格的熵约简集.

反之，若B是对象导出三支概念格的熵约简集，假设存在某个b′∈B，使得B-{b′}是OEG协调集，则对任意x∈U，x< ·AT>·AT=x< ·B-{b′}>·B-{b′}，即H(B-{b′})=H(AT)，从而B-{b′}是对象导出三支概念格的熵协调集，这与B是对象导出三支概念格的熵约简集矛盾，故B是OEG约简集.

3 决策形式背景的熵属性约简

定义7设S=(U，AT，I，D，J)是一个决策形式背景，AT∩D=∅，其中，AT，D分别称为决策形式背景的条件属性和决策属性.若H(D|AT)=0，则称S是对象导出三支熵协调的决策形式背景.

为方便起见，下面称对象导出三支熵协调决策形式背景为三支熵协调决策形式背景.

表2 决策形式背景(U，AT，I，D，J)Tab.2 Decision formal contexts (U，AT，I，D，J)

例3设S=(U，AT，I，D，J)是一个决策形式背景，其中，U={1，2，3，4，5}，AT={a，b，c，d，e}，D={f，g，h}，如表2所示.

经计算得1< ·AT>·AT={1}，2< ·AT>·AT={2}，3< ·AT>·AT={3}，4< ·AT>·AT={4}，5< ·AT>·AT={5}，1< ·D>·D={1，4}，2< ·D>·D={2}，3< ·D>·D={3，5}，4< ·D>·D={1，4}，5< ·D>·D={3，5}，由于H(D|AT)=0，故S是三支熵协调决策形式背景.

定义8设S=(U，AT，I，D，J)是三支熵协调决策形式背景，对B⊆AT及其对象导出三支概念格的条件信息熵H(D|B)，若满足H(D|B)=H(D|AT)，则称B是对象导出三支概念格的熵协调集.对B⊆AT，有H(D|B)=H(D|AT)，且对任意B′⊂B，都满足H(D|B′)≠H(D|AT)，则称B为对象导出三支概念格的熵约简集.记其核心属性集为coreD(AT).

定理10设S=(U，AT，I，D，J)是三支熵协调决策形式背景，对于任意a∈AT，a为非核心属性当且仅当H(D|AT-{a})=0.

证明:S是三支熵协调决策形式背景，故H(D|AT)=0.由于a为非核心属性，故而AT-{a}为对象导出三支概念格的熵协调集，从而H(D|AT-{a})=H(D|AT)，也即H(D|AT-{a})=0；反之，若H(D|AT-{a})=0，则有AT-{a}为对象导出三支概念格的熵协调集，故a为非核心属性.

定理11设S=(U，AT，I，D，J)是三支熵协调决策形式背景，B⊆AT，B是对象导出三支概念格的熵约简集当且仅当对于其对象导出三支概念格的条件信息熵H(D|B)，有H(D|B)=H(D|AT)且对任意a∈B，H(D|B-{a})>0.

证明:B是对象导出三支概念格的熵约简集， 则B是对象导出三支概念格的熵协调集，则H(D|B)=H(D|AT)成立.而对于任意a∈B，显然有

假设存在某个b∈B使得H(D|B-{b})=0，则B-{b}为对象导出三支概念格的熵协调集，这与B是对象导出三支概念格的熵约简集矛盾，故任意a∈B，均有H(D|B-{a})>0.

若H(D|B)=H(D|AT)，则B是对象导出三支概念格的熵协调集.设存在C⊂B使得H(D|C)=0，则对任意x∈U都有x< ·C>·C⊆x< ·D>·D成立.而C⊂B，故存在a∈B使得x< ·B-{a}>·B-{a}⊆x< ·C>·C⊆x< ·D>·D，此时H(D|B-{a})=0，这与B是对象导出三支概念格的熵协调集矛盾，故B是对象导出三支概念格熵约简集.

定义9设S=(U，AT，I，D，J)是三支熵协调决策形式背景，对于a∈B⊆AT，记a在决策属性D下相对于属性集B的重要度为Sig(a，B，D)=H(D|B-{a})-H(D|B).令C=AT-B，对于任意b∈C在决策属性D下相对于属性集B的重要度记为SGF(b，B，D)=H(D|B)-H(D|B∪{b}).

定理12设S=(U，AT，I，D，J)是三支熵协调决策形式背景，对于任意a∈AT，a为核心属性当且仅当Sig(a，AT，D)>0.

证明:S是三支熵协调决策形式背景，则有H(D|AT)=0.a为核心属性当且仅当H(D|AT)≠H(D|AT-{a})，又因为H(D|AT-{a})≥0，从而H(D|AT-{a})>0，即a为核心属性当且仅当Sig(a，AT，D)>0.

推论1coreD(AT)={a|Sig(a，AT，D)>0}.

证明: 由定理12知.

上述内容虽只给出三支熵协调决策形式背景中核心属性的判别定理，并未给出非核心属性的区分方法，但仍可以获得约简集. 即通过Sig(a，AT，D)来确定核心属性集，判别核心属性集是否是约简集，若是则停止寻找；否则根据属性重要度SGF(b，B，D)选择恰当属性添加到核心属性中，直至获得对象导出三支概念格的熵约简集为止.

例4续例3，因为Sig(a，AT，D)=0， Sig(b，AT，D)=0， Sig(c，AT，D)>0， Sig(d，AT，D)=0， Sig(e，AT，D)=0，故c为核心属性.不妨取B={c}，此时H(D|B)≠0，因此B不是熵约简集.

下面依照属性重要度依次计算，事实上，只需计算H(D|B∪{b})这部分，选择H(D|B∪{b})值较小的属性添加即可.由于H(D|{ac})=0，H(D|{bc})>0，H(D|{cd})=0，H(D|{ce})=0，故重要度最大的三个属性分别为a，d，e，且此时a，d，e相对于B都是核心属性，因此对象导出三支概念格的熵约简集可以为{a，c}，{c，d}与{c，e}.

定义10设S=(U，AT，I，D，J)是三支熵协调决策形式背景，记条件属性AT和决策属性D之间的互信息I(AT，D)=H(D)-H(D|AT).

定义11设S=(U，AT，I，D，J)是三支熵协调决策形式背景，B⊂AT，a∈AT-B， 属性a对决策属性D的重要度函数: SGF(a，B，D)=(I(B∪{a}，D)-I(B，D))/H(D|{a})=(H(D|B)-H(D|B∪{a}))/H(D|{a}).

定理13设S=(U，AT，I，D，J)是三支熵协调决策形式背景，B⊆AT，若B是对象导出三支概念格的熵约简集当且仅当I(AT，D)=I(B，D)，且对任意a∈B，I(B，D)>I(B-{a}，D).

证明: 由定理11易得.

注1基于互信息中属性重要度的定义，给出了另外一种计算对象导出三支概念格的熵约简集的方式. 该方法引入了属性对于决策的重要性作为分子定义属性的重要度函数，改进了属性重要性的排序. 同样可通过找核心属性集，判别核心属性集是否是约简集，若是则停止寻找；否则根据互信息中属性重要度的定义，选择重要度最大的属性添加到核心属性中，直至获得约简集.

定义12[15]设S=(U，AT，I，D，J)是一个决策形式背景，若对任意x∈U均满足x< ·AT>·AT⊆x< ·D>·D，称是三支粒协调的决策形式背景.

定义13设S=(U，AT，I，D，J)是一个决策形式背景， 若存在B⊆AT， 对任意x∈U均满足x< ·B>·B⊆x< ·D>·D，称B是OEG协调集.若B是OEG协调集而任意的C⊂B均不是OEG协调集，则称B是OEG约简集.

定理14设S=(U，AT，I，D，J)是一个决策形式背景，若S是三支粒协调当且仅当S是对象导出三支熵协调.

证明: 若S是三支粒协调的决策形式背景，则对任意x∈U，都有x< ·AT>·AT⊆x< ·D>·D，显然有H(D|AT)=0，故S是对象导出三支熵协调.

若S是对象导出三支熵协调的决策形式背景，则H(D|AT)=0.对于任意x∈U，都有

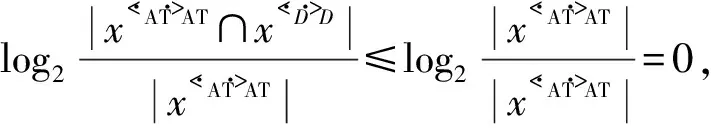
定理15设S=(U，AT，I，D，J)是三支熵协调决策形式背景，B⊆AT，若B是OEG协调集当且仅当B是对象导出三支概念格的熵协调集，B是OEG约简集当且仅当B是对象导出三支概念格的熵约简集.

证明: 若B是OEG协调集，对任意x∈U，有x< ·B>·B⊆x< ·D>·D，则H(D|B)=0，故B是对象导出三支概念格的熵协调集.

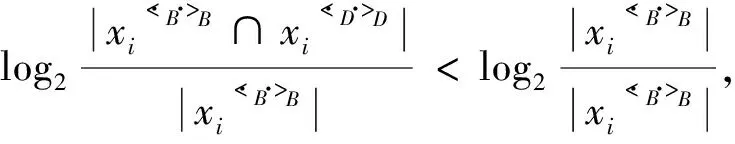
若B是OEG约简集，假设存在b0∈B，B-{b0}是对象导出三支概念格的熵协调集，则对任意x∈U，x< ·B-{b0}>·B-{b0}⊆x< ·D>·D，从而B-{b0}是OEG协调集，这与B是OEG约简集矛盾，故而B是对象导出三支概念格的熵约简集.

反之，若B是对象导出三支概念格的熵约简集，假设存在某个b′∈B，B-{b′}是OEG协调集，对任意x∈U，x< ·B-{b′}>·B-{b′}⊆x< ·D>·D，则H(D|B-{b′})=0，即B-{b′}是对象导出三支概念格的熵协调集，这与B是对象导出三支概念格的熵约简集矛盾，故而B是OEG约简集.

4 结束语

文中引入对象导出三支概念格的信息熵、条件熵和互信息等概念，分别在形式背景与决策形式背景上探讨了对象导出三支概念格的熵属性约简方法. 在此基础上，证明了对象导出三支概念格的熵协调集等价于OEG协调集，对象导出三支概念格的熵约简集等价于OEG约简集. 然而，文中仍有很多不足之处，如举例中的数据集较小，未设计算法和分析其时间及复杂度，未给出不完备形式背景中对象导出三支概念格的熵属性约简方法等，这些问题将在后续做进一步的研究.