行人对人行桥三分力系数的影响

2021-09-26徐亚琳胡海涛钱长照雷鹰陈昌萍

华侨大学学报（自然科学版） 2021年5期

徐亚琳，胡海涛，钱长照，雷鹰，陈昌萍

(1. 厦门大学建筑与土木工程学院，福建厦门 361005； 2. 厦门理工学院风灾害与风工程福建省重点实验室，福建厦门 361024)

人行桥一般建造在行人密集地段的城市高空或深山峡谷的景区里，大多采用轻质高强材料，结构较轻柔，对风荷载更敏感.同公路桥相比，人行桥的主梁高度更小、桥面更窄，所以处于桥面上的行人对人行桥气动外形的影响也更显著.桥梁断面的静力三分力系数是一组很重要的抗风设计参数，静力风荷载往往是桥梁的控制设计荷载[1]，而桥上通行的大量行人势必会改变主梁断面周围的流场，对桥梁的静力三分力系数造成影响.

目前，研究桥梁抗风问题的主要手段有计算流体力学(CFD)方法和风洞试验方法.文献[2-3]利用CFD方法和风洞试验方法计算桥梁的静风作用，并对比两种方法的结果，结果表明，CFD方法能够较为精确地模拟主梁断面的三分力系数.文献[4-5]利用CFD方法识别不同风攻角下的三分力系数结果，并研究雷诺数和来流湍流度对桥梁断面三分力系数的影响.文献[6-7]研究栏杆、中央稳定板和风屏障等桥面附属设施对桥梁断面三分力系数的影响.国内外对三分力系数影响因素的研究主要集中于截面外形和桥面附属物等方面[8-11]，而针对行人对桥梁断面三分力系数的影响研究较少.文献[12-13]通过风洞试验方法进行人-桥系统节段模型的测力试验，研究不同人群密度引起的主梁断面气动参数的变化规律.以上研究对于分析行人对桥梁的气动影响有一定的推动作用，然而，仅采用风洞试验方法并不能直观地获得流场的特性，具有局限性.CFD方法可以有效求解气流流经主梁断面时的流态[14]，将风洞试验方法与CFD方法相结合，可以更好地研究行人对桥梁断面静力三分力系数的影响.

本文以福建省厦门市健康步道的某行人密集路段的人行桥为工程背景，结合风洞试验方法和CFD方法，研究非对称桥梁断面在不同风嘴角度入流的情况下，行人密度和排列位置对三分力系数的影响.

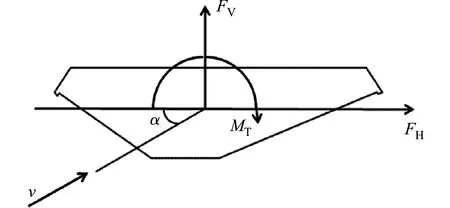
图1 桥梁断面三分力示意图 Fig.1 Tri-component forces on bridge section

1 三分力系数

三分力系数是描述具有相同形状的截面静力风荷载共同特性的无量纲参数[1].桥梁断面的三分力示意图，如图1所示.图1中：v为横向风的速度；FV为由于上、下表面压强的不同而在顺桥方向产生的升力；FH为由于前、后表面压强不同而在横桥方向产生的阻力；MT为由于升力与阻力的合力点与扭心不一致产生的扭矩[1].

上述三分力是按桥梁断面本身的体轴坐标系分解定义的，因此，称为体轴坐标系下的三分力(FV，FH，MT)，在风洞试验中是按风轴坐标系测定三分力的，即

(1)

体轴坐标系下，阻力系数函数为CH(α)，升力系数函数CV(α)及扭矩系数函数CT(α)和三分力之间的关系分别为

(2)

(3)

(4)

式(2)～(4)中：ρa为空气密度，ρa=1.225 kg·m-3；B为节段模型的宽度，m；D为节段模型的高度，m.

2 研究方法

厦门市某人行桥为单塔单侧悬挂的地锚式悬索人行桥，跨径布置为(216.7+10.0) m，全长226.7 m.桥梁主梁采用扁平钢箱结构，宽为4.4 m，梁高为1.2 m，标准段梁顶板宽为4.0 m，底板宽为0.9 m.主梁结构标准横断面，如图2所示.

图2 主梁结构标准横断面(单位：mm) Fig.2 Standard cross section of main girder structure (unit: mm)

考虑不同因素对桥梁断面气动参数的影响，主要针对桥上行人密度和桥上行人的横向排列位置对三分力系数的影响进行研究.

2.1 风洞试验方法

设计试验模型时，以工程实际模型为标准，满足几何形似准则，选取的几何缩尺比为1∶20.模型长为1.00 m，宽为0.22 m，长宽比为4.55(大于2.50)，满足抗风规范要求[15].模型桥面净宽为0.20 m，截面高度为0.06 m，栏杆的附加透风率为85%.模型骨架选用铝合金方管，外衣则采用木板制作，主梁上的人行道栏杆采用ABS(丙烯腈/丁二烯/苯乙烯共聚物)板制作，并模拟了栏杆的形状与透风率.模型需具有足够大的刚度，避免试验时出现较大振动，模型主要尺寸的加工误差控制在2%以内[16].以2014年国民体质监测公报的体质指标平均数作为参考，试验用的人体微缩模型采用几何缩尺比1∶20的，人体微缩模型的高度约为(8.0±0.5) cm.相较于长方体模型，人体微缩模型更加接近真实人体外形，人体四肢等细节表现更加精细准确.试验在厦门理工学院风洞实验室进行，其中，风洞低速试验段尺寸为25.0 m×6.0 m×3.6 m，低速段风速范围为0.5～30.0 m·s-1.采用美国高精度6分量测力天平测试桥梁断面的三分力，测力天平与测试模型连接，专用采集仪和计算机相连进行数据采集，数据的采样频率为1 000 Hz，采样时间为180 s，匀速风场的来流风速为10 m·s-1.

2.2 CFD方法

根据条带假定，假定桥梁足够长且平直，任一断面的风荷载可以代表其他断面的风荷载[1]，采用CFD方法模拟模型研究静力三分力系数问题.桥梁断面模型采用和风洞试验模型相同的几何尺寸，将计算区域划分为网格加密区、次加密区与非加密区，分别对应近壁面区域S1，尾流区域S2，外流区域S3.定义主梁断面计算区域的入口边界为速度入口边界的条件，出口边界为压力出口边界的条件，上下边界为对称边界条件，具体的模型计算区域及边界条件，如图3所示.选择求解模型为SSTk-ω模型，湍流强度为0.5%[17]，压力插值方法为二阶格式，采用SIMPLE算法处理压力与速度的耦合.

图3 主梁断面计算区域及边界条件 Fig.3 Calculation domain and boundary condition of main girder section

3 行人密度对三分力系数的影响

3.1 工况设置

文献[18-19]建议行人交通级别确定桥面允许的最大行人密度(ρp)为1.5 人·m-2，文中设置5种不同行人密度工况，分别为 0，0.2，0.5，1.0，1.5 人·m-2，行人的排列方式采取列队式排列方式，等间距分布在桥面上.

(a) A侧入流 (b) B侧入流图4 不同入流示意图 Fig.4 Inflow conditions in different directions

(a) ρp=0 人·m-2 (b) ρp=1.0 人·m-2图5 试验模型 Fig.5 Test model

定义从小风嘴角度一侧的入流状况为A侧入流；定义从大风嘴角度一侧的入流状况为B侧入流.不同入流示意图，如图4所示.由图4可知：桥梁断面模型为非对称形状，图4(a)的入流风嘴角度小于图4(b)的风嘴角度.由于风的方向具有不确定性，需考虑入流风从左、右两侧分别流入时的情况.针对5种行人密度工况，分别测试在风攻角为-12°～12°，角度间隔为1°的25个风攻角下的桥梁断面的三分力.行人密度分别为0和1.0 人·m-2的试验模型，如图5所示.选取体轴坐标系下的三分力系数进行分析，将风洞试验得到风轴三分力的数据通过式(1)～(4)转换成体轴三分力系数.

3.2 A侧入流的三分力系数变化规律

为了研究行人密度变化对桥梁断面三分力系数的影响，对A侧小风嘴入流的的5种不同行人密度工况的风洞试验结果进行分析.A侧入流的不同行人密度工况下的三分力系数试验结果，如图6所示.

由图6(a)可知：阻力系数随着风攻角变化而发生改变，在风攻角为-12°～10°范围内，阻力系数整体呈现先增大后减小的趋势，各个行人密度下的阻力系数在-4°～0°间达到峰值，当行人密度变化时，阻力系数也随之改变；而在负风攻角范围内，风攻角一定时，阻力系数随着行人密度的增大而增大；但在正风攻角范围内，则出现明显的不同.当风攻角为2°～ 6°范围内，行人密度为0.2 人·m-2的工况的阻力系数超过行人密度为0.5 人·m-2的工况，风攻角为7°～ 9°时，行人密度为0.2 人·m-2的工况的阻力系数进一步超越行人密度为1.0 人·m-2的工况，而行人密度为0.5 人·m-2的工况阻力系数更加趋近于桥面无人的工况.

由图6(b)可知:不同行人密度工况的升力系数变化规律基本一致，行人密度稀疏(0，0.2 人·m-2)的工况升力系数非常接近，行人密度较密集(0.5，1.0，1.5 人·m-2)的工况升力系数非常接近；不同行人密度工况的升力系数在小风攻角范围内差异较大，而在较大的风攻角范围内的升力系数出现交叠现象，数值比较接近，因此，较大攻角范围内的升力系数受桥上行人密度的影响较小；在从负风攻角转向正风攻角过程中，竖向力由向上的升力转为向下的压力，在行人密度较小、风攻角为2°时，竖向力由正转负，在行人密度较大、风攻角为-1°时，竖向力由正转负.

由图6(c)可知:扭矩系数的变化规律和升力系数的变化规律类似，在旋转风攻角的过程中，多次出现不同行人密度的扭矩系数曲线交叠的情况；在从负风攻角转向正风攻角过程中，扭矩方向发生改变，在行人密度较小、风攻角为8°时，扭矩由正转负，在行人密度较大、风攻角为5°时，扭矩由正转负.

(a) 阻力系数 (b) 升力系数 (c) 扭矩系数图6 A侧入流时不同行人密度工况下的三分力系数试验结果 Fig.6 A-side inflow tri-component force coefficients test results under different pedestrian density conditions

挡风面积是阻力系数的一个重要影响因素[20].当行人密度逐渐增大时，挡风面积也逐渐开始增大，导致阻力系数也将随之增加.当行人密度增大至一定值时，挡风面积将成为影响阻力系数变化的最主要因素.因此，风攻角为-12°～12°的范围内，行人密度为1.0，1.5 人·m-2的工况下的阻力系数均处于极大值状态，且两者数值非常接近.但当行人密度稀疏时，挡风面积迅速减少，此时，阻力系数变化的主导因素为风攻角的变化.

根据试验结果发现，阻力系数在负风攻角范围内的变化规律明显，在正风攻角范围内变化规律复杂，特别是风攻角为6°时还出现了多个密度工况阻力系数重叠的现象，所以分别取风攻角为-6°，6°的数值模拟结果进行分析.A侧入流数值模拟绕流结果图，如图7所示.图7中：p为压强.

(a) 风攻角为-6°的压力分布云 (b) 风攻角为-6°的速度流线

由图7(a)可知：由于桥梁的迎风面为正压集中区域，背风面为负压集中区域，在风攻角为-6°的条件下，增大入流处的挡风面积，桥梁入流风嘴下缘及栏杆处为高压状态.

由图7(b)可知：气流不能快速通过桥面，桥面上形成低压区域，因此，桥面位置形成明显的气流涡旋.与之相反，由图7(d)可知：在风攻角为6°的条件下，由于风嘴较小的气流能够快速通过桥面和风嘴下缘，仅在桥梁栏杆处形成高压区域，最终气流聚集在断面的出流风嘴下缘，形成明显的涡旋.显然，处在断面尾部的气流漩涡对三分力系数的影响较大，所以在正风攻角范围内，风攻角度是阻力系数的主要影响因素.

由图7(c)可知：截面的上、下表面为负压集中区域，主梁的上表面压力大于下表面，所以在正风攻角范围内，呈现向下的压力状态.

3.3 B侧入流的三分力系数变化规律

对B侧的大风嘴入流时的5种不同行人密度工况的风洞试验结果进行分析，B侧入流的不同行人密度工况的三分力系数试验结果，如图8所示.由图8可知：行人密度为0.2，0.5 人·m-2工况的三分力系数非常接近，而行人密度为1.0，1.5 人·m-2工况的三分力系数非常接近.

(a) 阻力系数 (b) 升力系数 (c) 扭矩系数图8 B侧入流的不同行人密度工况下的三分力系数试验结果 Fig.8 B-side inflow tri-component force coefficients test results under different pedestrian density conditions

由图8(a)可知：随着行人密度的增大，阻力系数也逐渐增大，当风攻角由-12°转至12°时，阻力系数与A侧入流的结果一样，呈现先增大后减小的趋势，阻力系数的峰值出现在风攻角为-6°附近；B侧大风嘴入流下的阻力系数在1.3～2.1之间，整体大于A侧小风嘴入流的结果；在负风攻角范围内，阻力系数由行人密度主导变化，所以不同行人密度下的阻力系数差值较大，在正风攻角范围内，阻力系数数值由风攻角主导变化，所以不同行人密度工况下的阻力系数数值越来越接近.

由图8(b)可知：行人密度变化对B侧入流的升力系数影响一样较小，但B侧入流的升力系数随风攻角的变化规律和A侧入流的结果相比有较大不同，各行人密度工况下的升力系数随着风攻角的变化先增加后减小，但拐点出现在不同的风攻角处，行人密度为0，0.2，0.5 人·m-2工况的峰值出现在风攻角为0°附近，行人密度为1.0和1.5 人·m-2工况的峰值则出现在风攻角为3°附近.

由图8(c)可知：B侧入流的扭矩系数的变化规律较为复杂，多次出现波动现象，在正风攻角范围内的扭矩系数差异较大.

B侧入流数值模拟绕流结果图，如图9所示.由图7(a)，(c)及图9(a)，(c)可知：A，B两侧入流的压力分布情况基本一致.

由图9(a)可知：截面的迎风面为正压集中区域，背风面为负压集中的区域，截面前后的压差较大，所以此时阻力系数较大.

由图9(b)，(d)可知：风攻角为-6°时，尾流区的表面积较大，桥面上的涡旋位置较A侧入流时更靠后；风攻角为6°时，截面底部的气流涡旋现象更加明显.

(a) 风攻角为 -6°的压力分布云图 (b) 风攻角为-6°的速度流线图

(c) 风攻角为 6°的压力分布云图 (d) 风攻角为6°的速度流线图图9 B侧入流的数值模拟绕流结果图 Fig.9 Numerical simulation circumfluence flow results of B-side inflow

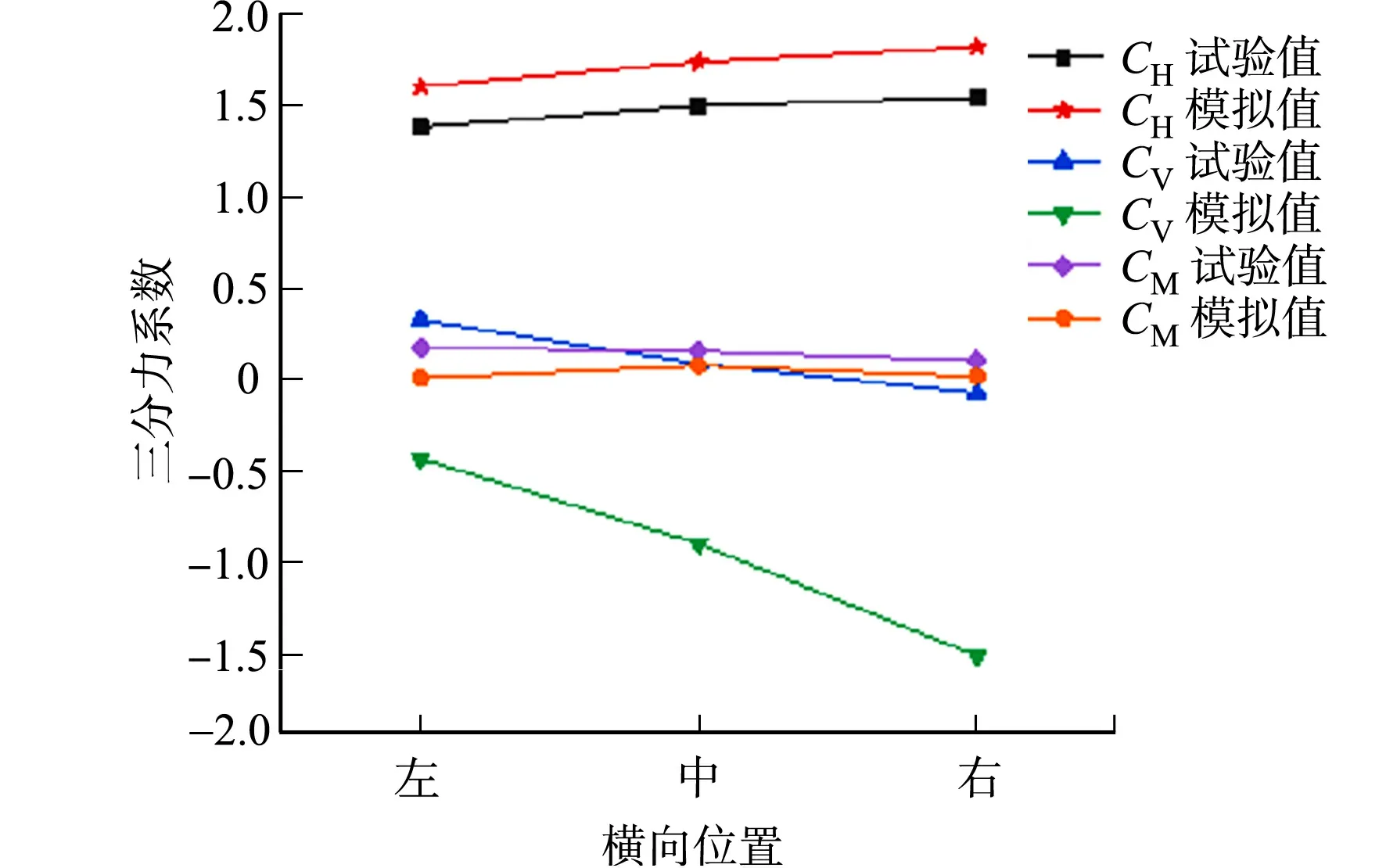
图10 不同横向排列位置下的三分力系数结果 Fig.10 Tri-component force coefficients results under different lateral positions

4 行人横向排列位置对三分力系数的影响

除了桥上行人密度对三分力系数有影响外，桥上行人排列的横向位置也会影响三分力系数.试验取行人密度为0.2 人·m-2，即桥上有15个行人等间距地排列成纵排，按迎风面、桥中心和背风面分为左、中和右三个区域.不同横向排列位置下的三分力系数结果，如图10所示.由图10可知：随着行人从左侧移动至右侧，阻力系数逐渐增大，而扭矩系数基本不变，试验值与模拟结果基本一致；但升力系数出现明显下降的趋势，并且模拟数值远低于试验结果.这是由于风洞试验采用的是三维模型，沿桥面等间距分布的行人对不同区域的升力系数作用并不同，对整体桥梁的影响并非简单的叠加状态，而CFD方法模拟的是二维模型，相当于是截取桥梁长度方向的某一截面采集结果，因此，二维模型模拟与风洞试验结果的升力系数有明显误差，关于行人的排列方式对桥梁断面的升力系数影响还需后续深入研究.

不同横向排列位置下压力等值线图，如图11所示.由图11可知：行人前部的迎风面为正压最大区，而桥梁截面的下表面和背风面是负压集中的区域；随着行人由桥面左侧移动到右侧，压力最大区域也逐渐覆盖桥梁截面的上部分，截面下表面和背风面的负压越来越大，此时，上、下表面的压差越来越大.这也和图10中的升力系数的变化趋势相吻合.