箱梁剪力滞效应分析的有效宽度法对荷载类型适应性研究

李 晶,张元海

(兰州交通大学土木工程学院,兰州 730070)

在现代桥梁向大跨度、轻型化发展的过程中，宽箱梁在实际工程中的应用已较为普遍，学者们对宽箱梁剪力滞效应所做的研究日渐成熟。从概念分析的理论层面[1-4]到考虑工程实际的应用层面[5-6]，从钢筋混凝土箱梁[7]到波形钢腹板箱梁[8-12]，相关文献已有不少。箱梁在竖向荷载作用下弯曲时，翼板剪切变形使纵向应力沿截面横向分布不均匀，在顶、底板与腹板交接处出现应力峰值，离腹板越远，应力越小，这种现象被称为剪力滞效应。实际工程中若根据剪力滞理论计算箱梁截面的精确应力解较为繁杂，考虑到工程安全且计算方便，设计规范中引入“有效宽度”的概念。

各国规范对有效宽度取值均有明确规定，我国规范中仅对单箱室混凝土桥梁的有效宽度作了规定，学者们将其研究拓展到组合梁或多箱室截面。孙理想[13]按照中国规范和美国AASHTO规范对承受静载作用的单箱双室箱梁的有效宽度进行了研究；王富平[14]对承受自重和移动荷载作用的单箱多室箱梁的有效宽度进行了研究，两人均是基于中美规范中单箱单室有效宽度的取值，将其扩展到单箱双室和单箱多室箱梁。在钢桥和组合梁桥方面，董桔灿等[15]对波形钢腹板组合连续梁桥翼缘有效宽度进行了研究，得出波形钢腹板箱梁桥截面有效宽度取值应介于普通混凝土箱梁和钢箱梁之间；赵秋等[16]对钢桥面板在车辆荷载和疲劳荷载作用下的有效宽度进行了研究，提出了一种可简便计算钢桥面板疲劳的方法；此外还有其他有关有效宽度的研究成果[17-18]。其中，对箱形截面梁有效宽度的研究中，主要是对不同材料和不同截面的梁桥在不同荷载作用下的有效宽度取值进行对比分析，为我国规范中有效宽度取值的修订提供参考。然而，对于我国JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[19]和TB 10092—2017《铁路桥涵混凝土结构设计规范》[20]中箱梁有效宽度的应用不区分荷载类型的情况，尚未见有相关文献分析有效宽度法对不同荷载类型的适应性。

选取一简支箱梁为算例，梁上分别作用集中荷载和均布荷载，根据能量变分法给出应力解析解的计算公式，建立ANSYS模型以验证解析解的正确性。将规范中有效宽度法计算的截面应力与解析解进行比较，根据应力误差分析有效宽度法对集中荷载和均布荷载的适应程度，并对分析结果提出相应的解决方法。

1 现行桥梁设计规范中的有效宽度法

有效宽度的含义为：将箱梁顶板净宽一半b1、底板净宽一半b2、悬臂板净宽b3分别按照相应的有效宽度折减系数折减为bm1、bm2、bm3，使得折减后的截面按初等梁理论计算的应力与未折减截面考虑剪力滞效应的最大应力相等，如图1所示。其中，tt、tb分别为顶板、底板与腹板交接处内外折角点间的水平距离，σmax为应力峰值。图1右半部分中的曲线所围成的面积与矩形面积相等，曲线表示上下翼缘的实际应力分布状态，矩形宽度为折减后的截面宽度。

图1 箱梁应力分布及有效宽度

有效宽度的取值主要受宽跨比、荷载类型、支承条件、截面形状及尺寸、截面在梁跨内的位置等因素影响。公路规范和铁路规范对有效宽度的规定均是折减系数乘以原来的宽度，但两种规范中对折减系数的规定却不尽相同。

公路规范中的折减系数由公式计算，以宽跨比为变量，中部梁段与支点及悬臂段的折减系数计算公式不完全相同，具体的计算公式参见文献[19]中4.3.4节。

铁路规范中的折减系数根据宽跨比查表取值，具体取值参见文献[20]中4.3.3节。

在两种规范中，对有效宽度的规定没有区分荷载类型，无论桥梁上作用均布荷载还是集中荷载，计算应力时所用的有效宽度相同。但集中荷载与均布荷载作用下的剪力滞沿跨长的纵向效应并不相同，应用规范中有效宽度法计算截面应力时仍采用相同的有效宽度值，其应力结果的精度有待商榷。针对问题选取一简支箱梁进行研究，通过分析有效宽度法计算的集中荷载、均布荷载作用下的应力结果的精度，对规范有效宽度法在应用时应区分荷载类型的必要性进行说明并提出相应的建议。

2 能量变分法求解析解

2.1 剪力滞翘曲应力及广义力矩

采用文献[21]中的剪力滞翘曲位移函数，其在传统翘曲位移函数的基础上，考虑悬臂板与顶板约束条件的不同，引入约束特性修正系数，有效地解决了悬臂板宽度与顶板半宽相同时悬臂板端部与顶板中部应力不应相同的问题，客观地反映了悬臂板的应力分布状态，使计算的剪力滞翘曲应力更接近实际值。与文献[21]推导时采用的矩形截面不同，本文采用梯形截面。

以简支箱梁为例，截面如图2所示。梁长为l，梁上作用分布荷载p(z)，梁体弯曲时的应力可分为由初等梁理论计算的弯曲正应力和由剪力滞效应引起的翘曲应力。在此主要分析翘曲应力，以附加挠度为广义位移，以顶板位移函数为基准，对底板引入宽度和相对位置修正系数，对悬臂板引入宽度和约束特性的修正系数。剪力滞效应引起的箱梁横截面上任一点的纵向位移u(x，y，z)表达为

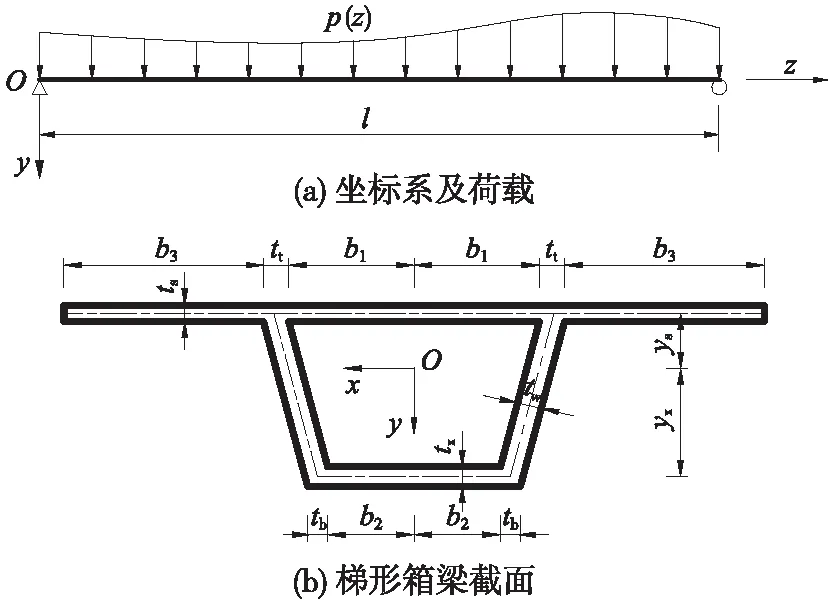
图2 简支箱梁荷载及截面

u(x，y，z)=-ω(x，y)f′(z)

(1)

式中，ω为剪力滞广义翘曲位移函数；f为剪力滞效应引起的附加挠度。

ω(x，y)=y-η[ξ+ωs(x，y)]

(2)

式中，η和ξ为剪力滞翘曲应力在横截面上需满足的弯矩和轴力自平衡修正系数；ωs为剪力滞基本翘曲位移函数。

本文选用的ωs计算公式如下

ωs(x，y)=

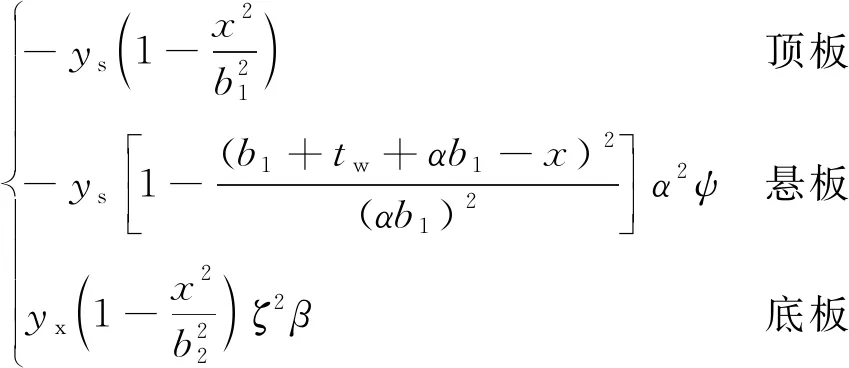
(3)

式中，ys和yx分别为箱形截面水平形心轴到上翼缘板中面和下翼缘板中面的距离；ts、tb和tw分别为上翼缘板、下翼缘板和腹板厚度；ψ为考虑悬臂板边界约束特性的修正系数，ψ取1.4；α=b3/b1，ζ=b2/b1，β=yx/ys。

由弹性力学中的物理关系和几何关系可得

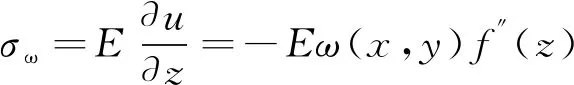
(4)

式中，E为弹性模量。

剪力滞效应引起的翘曲应力在横截面上合成的弯矩和轴力为0，由此可解得η和ξ值。

翘曲应力对应的广义力矩Mω为

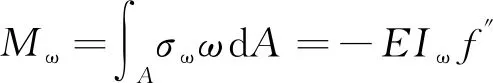
(5)

(6)

式中，Iω为剪力滞翘曲惯性矩。

翘曲应力σω的计算公式为

(7)

横截面上的总弯曲正应力σ为

σ=σ0+σω

(8)

式中，σ0为初等梁理论计算的弯曲正应力。

2.2 控制微分方程及其解

箱梁在剪力滞状态下的总势能为Π，根据最小势能原理，总势能的一阶变分为零，从而可得剪力滞状态下的控制微分方程及边界条件。

(9)

式中，G为剪切模量。

δΠ=0

(10)

由式(10)可得控制微分方程为

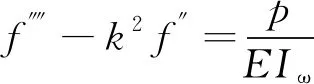
(11)

其中，k为Reissner参数

(12)

式中，As为剪力滞翘曲面积。

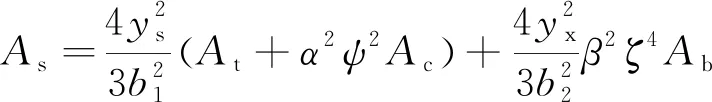
(13)

式(11)的通解为

f(z)=C1+C2z+C3shkz+C4chkz

(14)

在荷载p(z)作用下，式(11)的特解为

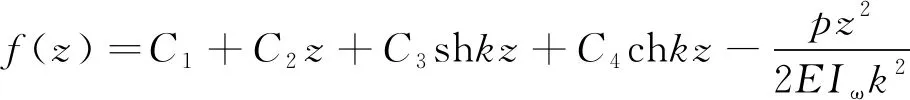
(15)

求解式(15)的边界条件如下。

固定端：f=0，f′=0；

简支端：f=0，f″=0；

自由端：f″=0，f‴-k2f′=0。

当简支梁上作用均布荷载q时，由式(15)和相应的边界条件可解得系数C1～C4。简支箱梁在均布荷载作用下的附加挠度f和剪力滞广义力矩Mω分别为

(16)

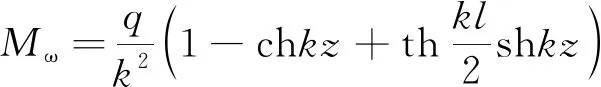
(17)

当简支梁的跨中作用集中荷载P时，附加挠度f和剪力滞广义力矩Mω分别为

(18)

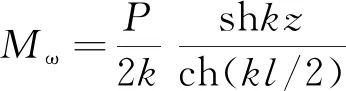
(19)

3 算例分析

简支箱梁跨径l=50 m，截面尺寸如图3所示，材料特性为E=3.1×104MPa，μ=1/6，分别在跨中腹板顶面上对称作用一对集中荷载2P=2×10 kN及整跨腹板顶面对称作用均布荷载2q=2×1 kN·m-1。分别计算两种荷载作用下的腹板与顶底板交接位置处的应力解析解，将有效宽度法计算的应力值与解析解进行对比。

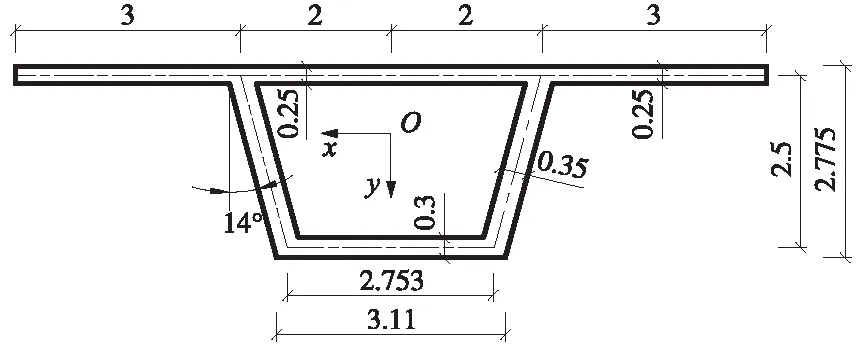
图3 箱梁截面尺寸(单位：m)

利用Shell63单元建立ANSYS模型，以验证本文应力解析解的正确性。取l/4和l/2截面的计算结果进行对比，结果如表1所示。

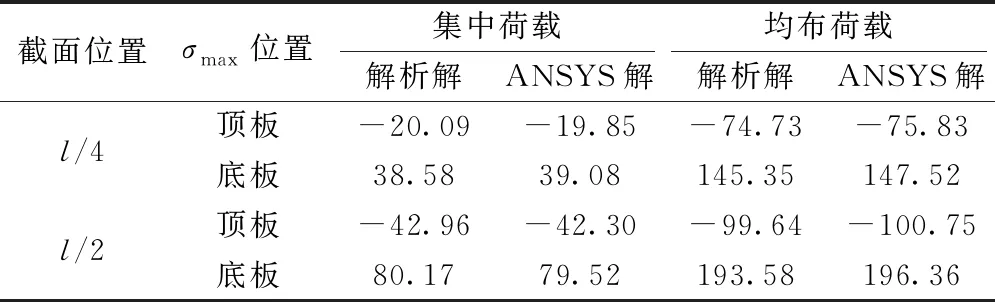
表1 解析解与ANSYS解的对比 kPa

由表1可知，本文方法计算的解析解与ANSYS解吻合良好，验证了解析法计算应力解的正确性。

3.1 算例中的有效宽度取值

文中算例的顶板和底板的宽跨比小于0.05，在公路规范中，顶板和底板有效宽度沿纵向取实际宽度，悬臂板有效宽度沿纵向有折减。铁路规范中，有效宽度折减系数根据宽跨比查表取值。3个翼板按规范有效宽度取值的纵向分布如表2所示。

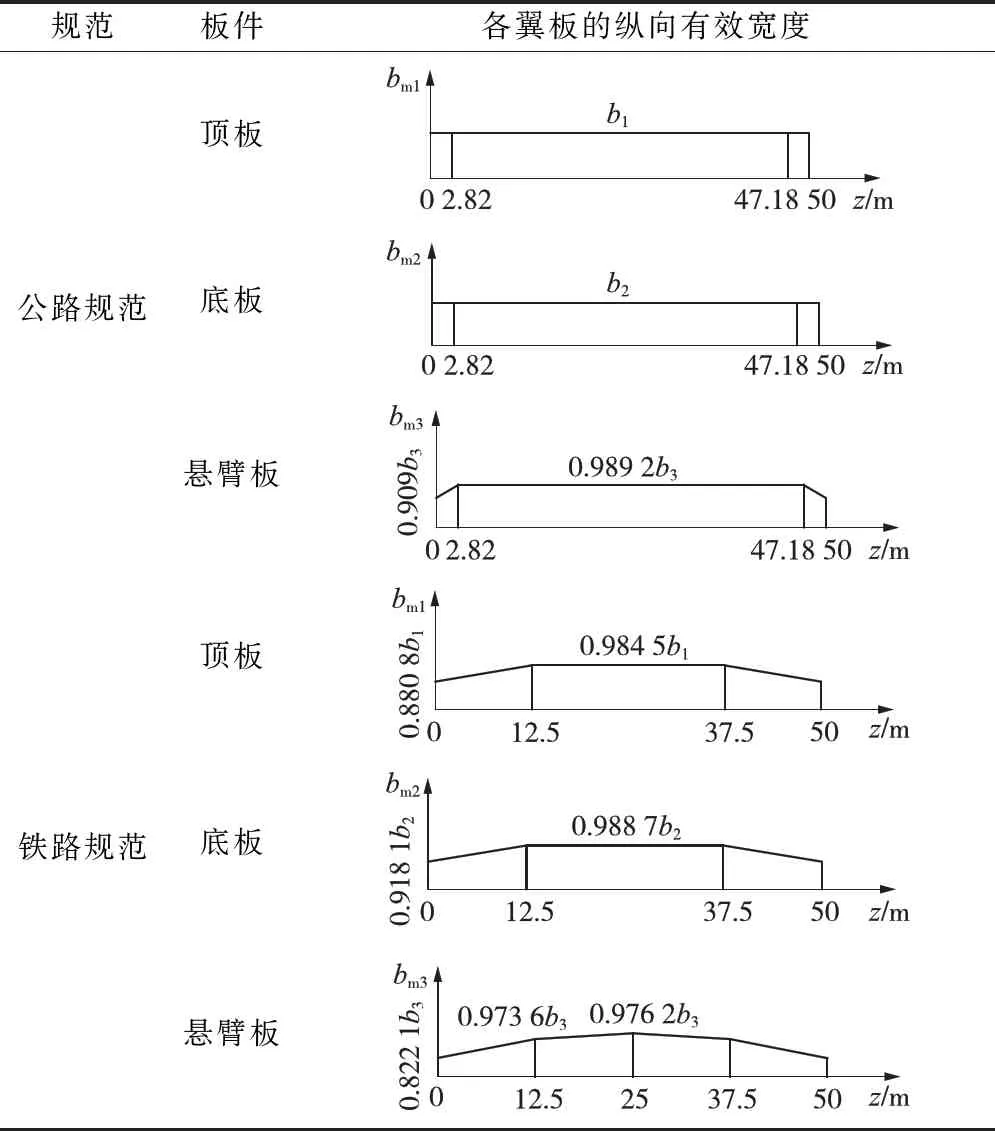
表2 各翼板沿纵向的有效宽度取值

3.2 应力分析

在集中荷载、均布荷载作用下，l/4和l/2截面分别按有效宽度法和本文解析法计算应力，以解析解为基础，对比分析规范中有效宽度法计算的截面应力精度，结果如表3、表4所示。

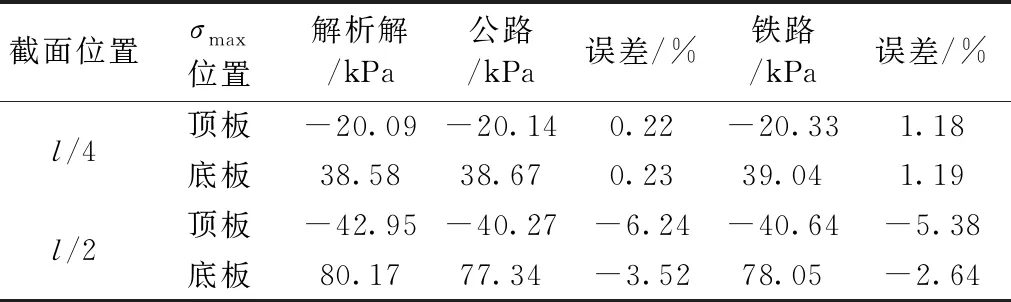
表3 集中荷载作用下的应力比较

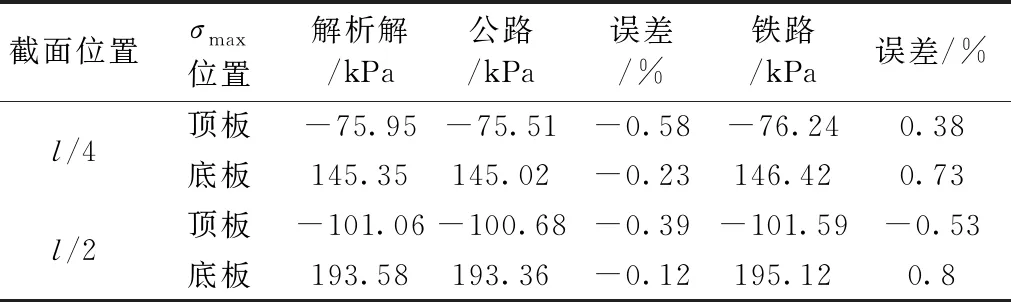
表4 均布荷载作用下的应力比较

由表3可以看出，l/4截面处的误差值小于集中荷载作用的l/2截面。公路规范的跨中应力误差达到-6.24%，铁路规范的跨中应力误差达到-5.38%，即规范中有效宽度法计算l/2处的应力时，有效宽度取值是偏大的，导致计算的应力值偏小，这样的应力值应用于工程中偏于不安全。

由表4可以看出，在均布荷载作用下，l/2和l/4截面的应力误差值均小于1%，表明有效宽度法计算的均布荷载作用下的截面应力结果是精确可靠的。

荷载作用下的剪力滞纵向效应为：集中荷载作用位置处的剪力滞效应较显著，但影响范围有限；集中荷载的作用位置离支座越近，剪力滞效应越显著。均布荷载作用下的剪力滞纵向效应由跨中向支座处逐渐增大。取整跨的应力误差进行分析，结果见图4、图5，图中的误差计算式与表3、表4中的相同。

图4 集中荷载下的顶底板应力误差

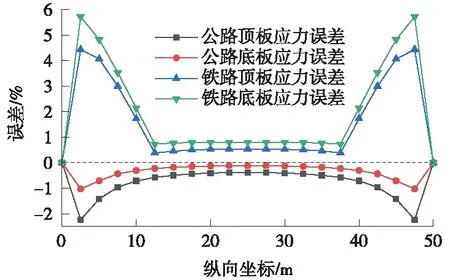
图5 均布荷载下的顶底板应力误差

由图4可知，整跨范围内，梁端附近及跨中(荷载作用位置)附近的误差曲线较陡，曲线在跨中位置下凹，表明有效宽度法计算的应力值偏小，有效宽度折减系数偏大；曲线在梁端附近上凸，表明有效宽度法计算的应力值偏大，规范中该梁段内有效宽度折减系数偏小。结合集中荷载下的剪力滞纵向效应可知，若要增大有效宽度法对集中荷载的适应性，梁端附近的截面应在原规范的基础上增大折减系数或截面不进行折减；跨中附近的梁段内应减小折减系数以充分考虑剪力滞效应。

由图5可知，均布荷载作用下的误差曲线大体平缓且接近于0，表明规范中的有效宽度取值更适合计算均布荷载作用下的应力。梁端附近误差曲线出现峰值，是因为规范中有效宽度考虑到均布荷载作用下梁端附近剪力滞效应较大，对截面宽度进行了较大的折减，但在应力计算中，梁端附近的弯矩较小，故计算的应力值较小，从而出现较大误差。

由图4、图5可以看出，公路规范的误差曲线比铁路规范的误差曲线更接近0，表明公路规范的有效宽度取值较合理，铁路规范取值相对较保守。对比图4、图5可知，规范的有效宽度取值并非对集中荷载和均布荷载都有相同的适应性，故规范有效宽度法的应用应区分集中荷载和均布荷载。由图5可知，现行规范有效宽度法对均布荷载有较好的适应性；为使现行规范的有效宽度法同样于集中荷载，对规范有效宽度值进行修正，分别适用对公路和铁路规范的跨中截面有效宽度提出了相应的修正系数，充分考虑了集中荷载作用下的剪力滞效应，使计算结果偏于安全。

在修正时，对公路规范的中部梁段有效宽度折减系数乘以修正系数0.92；对铁路规范的跨中截面有效宽度折减系数乘以修正系数0.95。考虑到集中荷载下离荷载作用位置较远的梁段受剪力滞影响较小，无需对截面宽度进行折减来考虑剪力滞效应，故只对作为控制截面的跨中截面有效宽度进行了修正。为分析修正后的有效宽度法对集中荷载的适应性，对跨中截面按修正后的有效宽度法计算截面应力得到修正解，将修正前及修正后计算的集中荷载下截面应力与解析解进行对比，以误差1、误差2表示，结果如表5所示。

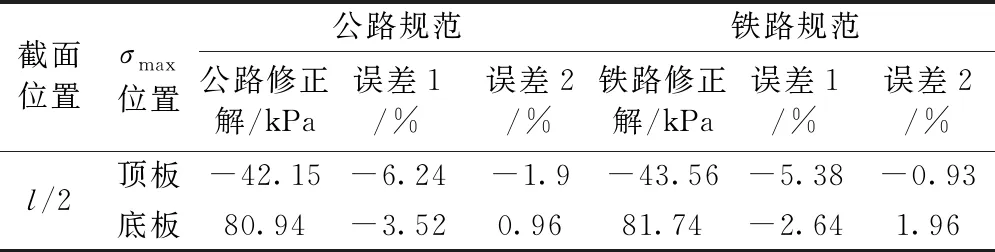
表5 修正前后有效宽度法计算的应力误差

由表5可知，修正后，作为控制截面的l/2处的计算结果增大，应力误差减小。即修正后的有效宽度法充分考虑了集中荷载作用位置处的剪力滞效应，使结果偏于安全，表明修正后的有效宽度法适应性良好。

4 结论

(1)现行桥梁设计规范中的有效宽度法对均布荷载的适应性较好，但对集中荷载的适应性较差。

(2)现行公路规范中的有效宽度取值较合理，铁路规范的有效宽度取值较保守。

(3)针对跨中作用集中荷载的情况，提出了公路规范的中部梁段有效宽度修正系数0.92，铁路规范的跨中有效宽度修正系数0.95，计算结果表明，修正后的有效宽度法对集中荷载的适应性良好。