40 t轴重重载铁路曲线超高对行车性能的影响规律分析

2021-09-26杨麦生王开云

铁道标准设计 2021年9期

周坤,王彦,杨麦生,王开云

(1.西南交通大学牵引动力国家重点实验室,成都 610031； 2.中铁第四勘察设计院集团有限公司国际事业部,武汉 430063)

铁路曲线段通常需设置一定的超高，以平衡列车通过曲线时的离心力，促使内外轨受力均衡。曲线超高的设置大小不仅影响轮轨受力状态，还与轮轨冲角以及转向架导向能力关系密切，进而对轮轨磨耗和滚动接触疲劳产生重要影响。大量现场数据统计和相关研究表明，合理设置超高能够起到减缓轨道伤损病害发展的作用[1-4]。目前，各国正朝着大轴重铁路方向发展，大轴重重载运输已成为大宗货物最为经济有效的运输方式[5-7]。然而随着轴重的增加，轨距扩大、钢轨侧磨、轨顶磨耗、鱼鳞状裂纹(图1)等现象也将随之加重，势必对曲线超高提出更高的设计要求。

图1 钢轨疲劳裂纹

许多学者针对曲线超高的合理选取开展了大量研究，王开云[8]运用车辆-轨道耦合动力学理论，分析了高速铁路曲线轨道欠、过超高条件下的轮轨动力特性；孔凡兵[9]针对新建时速120 km地铁线路曲线超高和缓和曲线长度进行了理论分析，并结合国内外相关规范给出了两参数的建议值；陈旭[10]分析了不同曲线超高下的轮轨受力状态以及曲线超高在铁路设计中的关键影响；李晓芹[11]计算分析了曲线超高、半径等圆曲线几何参数对车线动力响应的影响规律，从运行安全性和轮轨磨耗等方面研究了曲线各参数取值和匹配问题；赵德宽等[12]根据现场调查数据分析了不同未平衡外轨超高对侧磨速率的影响规律，提出了重载铁路小半径曲线外轨超高的设置建议；杨新文等[13]基于修正的轮轨非Hertz接触建立了详细的钢轨磨耗预测分析模型，以23 t轴重货车为例，深入研究了重载铁路平曲线超高对钢轨磨耗的影响。

从上述研究工作可以看出，曲线超高对列车运行性能有着重要影响，而我国尚缺乏30 t轴重以上铁路曲线超高的理论研究和设计规范。以40 t轴重重载铁路曲线超高为研究对象，基于动力学软件UM建立40 t轴重仿真模型，从运行安全性、轮轨磨耗以及疲劳损伤三个角度，研究40 t轴重重载铁路不同未平衡超高下的列车曲线通过性能，从而为40 t轴重铁路曲线超高设计提供技术支撑。

1 计算模型

40 t轴重列车采用两节货车为一单元的编组模式，同一单元两货车通过牵引杆(无车钩间隙)连接，不同单元之间通过车钩连接。基于动力学仿真软件UM，建立了40 t轴重四编组列车计算模型(图2)。其中，40 t轴重货车转向架仍采用传统的三大件模式，主要包括轮对、承载鞍、轴箱橡胶垫、侧架、斜楔、摇枕、心盘、常接触弹性旁承以及交叉拉杆；车钩为符合AAR标准的F70DE固定、FR209E旋转配套车钩，为了限制车钩的水平转动，车钩钩尾处设置了球面摩擦结构，且F70DE固定车钩还增添对中凸肩结构，以防止车钩失稳，缓冲器采用的是符合AAR M-901E的SL-76型橡胶型缓冲器，具有大容量、大行程、低阻抗、高能量吸收率的特点。

列车制动会造成货车间的纵向冲动[14-15]，为研究制动条件下，特别是大压钩力作用下列车的运行性能，将不同等级的压钩力以简化方式施加到四编组列车前后货车钩尾销处，由于40 t轴重货车采用的缓冲器最大阻抗力为2 200 kN，因此计算时将纵向压钩力分1 000、2 000 kN两个等级进行安全性评估，如图2中的力F所示。考虑到端部货车可能受到作用力施加方式而对分析结果产生影响，均选取第3节货车为研究对象。

图2 40 t轴重四编组列车模型

2 评价指标

2.1 安全性指标

在重载线路设计中，需首要满足重载列车安全运行的要求，常用的安全性评估指标有：脱轨系数、轮重减载率、轮轴横向力、轮轨垂向力。我国GB 5599—2019《机车车辆动力学性能评定及试验鉴定规范》规定脱轨系数、轮重减载率的安全限值分别为1.0、0.65；规定轮轴横向力不得大于15+P0/3，P0为静轴重，kN，对于40 t轴重货车，其安全限值为145.8 kN。

2.2 磨耗评价指标

20世纪80年代初，英国铁路部门提出了以轮轨接触斑处所消耗的摩擦功作为评价轮轨磨耗的指标，定义为蠕滑力合力与蠕滑率两个向量的向量积。

W2=Fε=FXεX+FYεY+MSPεSP

(1)

式中，Fx、FY、MSP分别为纵向、横向蠕滑力和自旋蠕滑力矩；εX、εY、εSP分别为纵向、横向蠕滑率和自旋蠕滑率。

大多数情况下，自旋蠕滑比重较小，若忽略自旋蠕滑的影响，式(1)简化为磨耗数(wear number)

W3=Fε=FXεX+FYεY

(2)

磨耗数认为轮轨磨耗量与轮轨蠕滑功线性相关，北美铁道协会运输试验中心所进行的现场试验，也证实了轮轨磨耗与接触斑处消耗的摩擦功有较好的线性关系。与此同时，英国铁路部门还在磨耗数的基础上提出了另一种衡量磨耗程度的表达形式，磨耗指数W3/A，即考虑了轮轨接触面积的影响，研究表明，磨耗指数在大磨耗状态下与实际磨耗情况更为吻合[16]。Lewis等通过双盘滚动试验分析了磨耗指数与磨耗速率的关系，如表1所示，按照磨耗机理的不同将整个磨耗过程分为3个阶段，其中，第1阶段黏着磨损主要是轮轨表面氧化层的磨损脱落，磨耗量相对较小；第2阶段剥层磨损为轮轨次表面出现明显的塑性变形和裂纹，进而导致薄条状材料脱离轮轨表面，此时磨耗量也显著增加；第3阶段金属磨损会造成大量的材料块脱落，但由于此阶段对应着更大的蠕滑和更小的接触面积，一般不太可能在实际的轮轨接触中出现这种情况[16-17]。

表1 磨耗指数与磨耗速率的关系[16]

综合来看，磨耗指数既包含了轮轨间蠕滑功、接触面积对轮轨磨耗的影响，同时又对大磨耗状态具有更好的预测性，因此本文选取磨耗指数作为轮轨磨耗的评价指标。

2.3 滚动接触疲劳评定

目前各国学者多采用损伤函数作为钢轨、车轮滚动接触疲劳损伤的预测模型。该预测模型利用磨耗数，能够考虑磨耗对疲劳损伤的影响，其损伤函数值表示车轮每滚动一圈或钢轨每通过一轮轴所产生的相对疲劳损伤，即当其累加值达到1时，可在车轮或钢轨表面产生肉眼可见的疲劳裂纹。

用于钢轨疲劳损伤预测的损伤函数曲线见图3。

图3 损伤函数曲线

由图3可以看出，在已知磨耗数的情况下，要得到对应的疲劳损伤值，还需确定3个磨耗数阈值β1、β2、β3的值。由于不同的线路、车辆类型常常需要对3个损伤系数进行重新标定，为了提高其适用性，相关文献[18-19]指出，假定材料为理想弹塑性，可根据材料的抗拉强度σy、屈服强度σUTS与材料剪切性能的关系求得剪切流动应力为

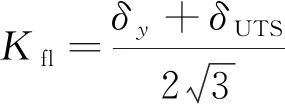
(3)

如果轮轨接触斑面积为A，则产生塑性变形所需的剪切力为

(4)

当蠕滑率ε低于0.1%时，无损伤出现；当蠕滑率ε为0.3%时，疲劳损伤达到最大值，即材料疲劳寿命最短；当蠕滑率ε为1%时，磨耗损伤开始占据主导地位[18]。由此，通过计算上述3种情况下的Fε确定对应的磨耗数阈值β1、β2、β3。

在得到每一时间步下的疲劳损伤值Di后，根据接触斑宽度2bi，将接触斑沿钢轨横截面宽度方向以1 mm间隔分成若干离散点，计算接触斑内各离散点的权重系数hi(y)(椭圆形分布，接触斑中心为1，边缘为0，如式(5)所示)，最后将基于磨耗数求得的疲劳损伤值Di与各离散点权重系数相乘，即可得到该时间步对应的钢轨横截面疲劳损伤值分布情况。

(5)

式中，yci为接触斑中心在轨面坐标系的横向坐标；y为各离散点在轨面坐标系的横向坐标。

另外，在计算钢轨疲劳损伤时，只计算纵向蠕滑力与运行方向相反的情况。这是由于该预测模型强调了表面液体(如润滑油或水)对疲劳裂纹扩展的加速作用，认为无液体的钢轨表面即使存在初始裂纹，裂纹也扩展较慢或不扩展[20]。

3 计算结果分析

基于上述建立的货车模型，将重点考察不同未平衡超高(欠超高为负值，过超高为正值)对40 t轴重重载列车运行性能的影响。其中，未平衡超高值计算范围-80～+80 mm，每隔20 mm取值，曲线半径800 m，缓和曲线长度120 m，货车运行速度80 km/h，轨道不平顺为美国五级谱。

图4为惰行工况下，脱轨系数、轮重减载率、轮轴横向力、轮轨垂向力最大值随未平衡超高值的变化图。从图4可看出，随着未平衡超高的增加，外轨侧脱轨系数、轮轨垂向力随之呈减小趋势，内轨侧相应指标随之呈增大趋势，轮重减载率随未平衡超高的变化趋势则与之相反。以一位轮对为例，在未平衡超高由-80 mm增加至80 mm的过程中，外轨侧脱轨系数、轮轨垂向力、内轨侧轮重减载率分别由0.17、315.01 kN、0.39减小至0.11、239.88 kN、0.07，其减小量分别为0.06、75.13 kN、0.32；内轨侧脱轨系数、轮轨垂向力、外轨侧轮重减载率分别由0.11、251.29 kN、0.04增加至0.20、307.72 kN、0.37，其增加量分别为0.09、56.43 kN、0.33，内、外轨侧各指标变化幅度大致相当。轮轴横向力随未平衡超高的增加呈先减小后增大的变化趋势，其中，一位轮对、二位轮对在未平衡超高分别为-20、+20 mm时达到最小值。由此可知，过大的欠、过超高均会加剧轮轨动力作用，不利于车辆安全运行。

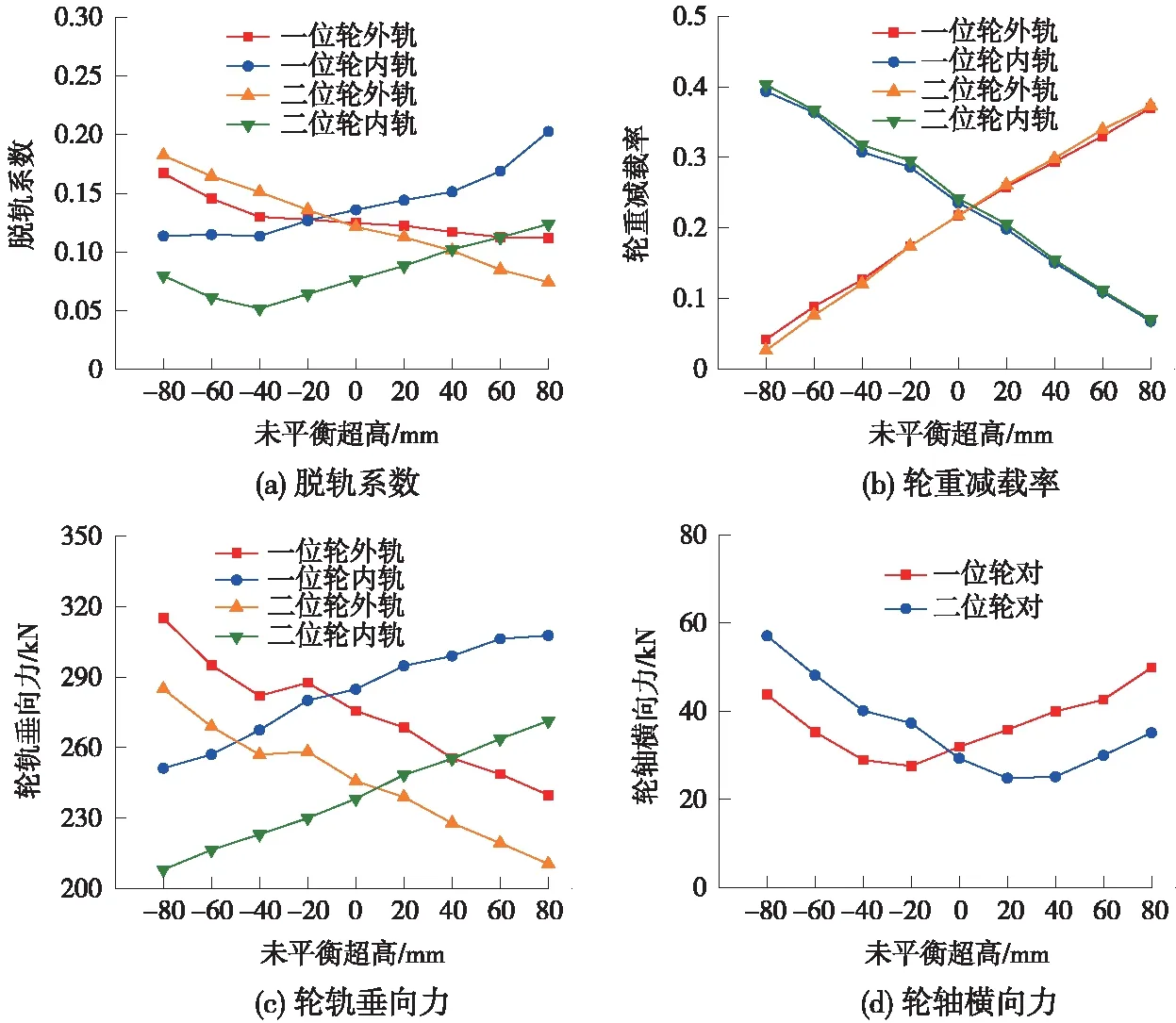
图4 不同未平衡超高对40 t轴重货车运行性能的影响

图5给出了不同纵向压钩力作用下，40 t轴重货车外轨侧脱轨系数、轮轨垂向力、轮轴横向力指标最大值随未平衡超高的变化。由图5可知，在各压钩力工况下，脱轨系数、轮轨垂向力、轮轴横向力指标随未平衡超高的变化趋势与惰行工况基本一致，但随着纵向压钩力的增加，轮轴横向力最小值点对应的未平衡超高值随之增大。在惰行工况下，轮轴横向力最小值对应的未平衡超高为20 mm，当纵向压钩力增加至1 000、2 000 kN时，对应的未平衡超高分别增大至40、80 mm。从纵向压钩力变化对各指标的影响来看，随着纵向压钩力的增加，脱轨系数和轮轨垂向力随之呈增大趋势，在欠超高80 mm和过超高80 mm工况下，纵向压钩力为2 000 kN时的脱轨系数相比于惰行工况各增大0.07、0.06，轮轨垂向力各增大22.04、23.60 kN；对于轮轴横向力而言，在欠超高工况下，纵向压钩力会导致轮轴横向力显著增大，但由于纵向压钩力会导致最小值点向过超高方向移动，因此，在过超高工况下，轮轴横向力随纵向压钩力的增加反而呈减小趋势。整体来看，由列车纵向冲动导致的纵向压钩力会加剧曲线段的轮轨动力作用，且在较大的欠超高工况下，轮轴横向力的增加幅度更为明显，不利于轨道的结构稳定性。

图5 压钩状态下不同未平衡超高对安全指标的影响

惰行通过曲线时，40 t轴重货车轮轨冲角最大值在不同未平衡超高下的计算结果如图6所示。由图6可知，随着未平衡超高的增加，一位轮对轮轨冲角呈增大趋势，二位轮对轮轨冲角呈先减小后增大的变化趋势，在0 mm未平衡超高附近达到最小值。这主要是因为车辆以欠超高状态通过曲线时，一位轮对轮轨冲角为正值，二位轮对轮轨冲角为负值(以曲线径向位置为中心，逆时针方向偏转为正)，如图7所示，随着曲线超高的增加，二位轮对向内轨侧偏移，导致一位轮对、二位轮对逆时针偏转，一位轮对不断偏离径向位置，而二位轮对需先偏向后偏离径向位置，造成一位轮对轮轨冲角呈增大趋势，二位轮对轮轨冲角呈先减小后增大的变化趋势。

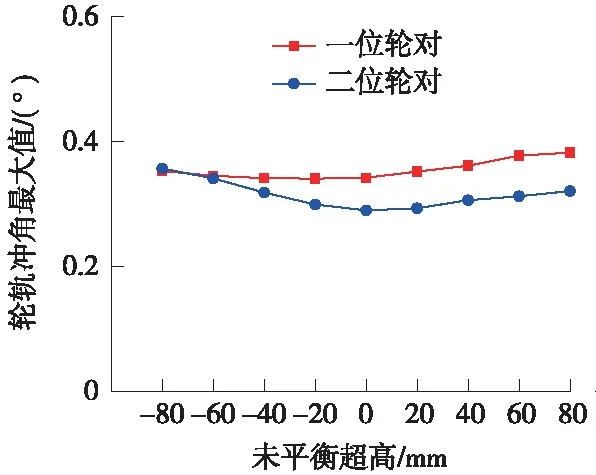
图6 不同未平衡超高对轮轨磨耗指标的影响

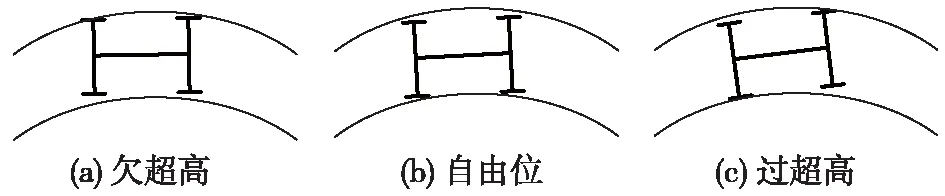
图7 转向架通过曲线时的位置状态

从图8所示的磨耗指数均方根值随未平衡超高的变化规律可看出，一位轮对外轨侧踏面接触点磨耗指数随未平衡超高的增加线性增大，轮缘接触点磨耗指数、一位轮对外轨侧总磨耗指数、一位轮对内轨侧磨耗指数以及二位轮对内、外轨侧磨耗指数随未平衡超高的增加均呈先减小后增大的变化趋势，最小值点对应的未平衡超高值分别为0、-20、+40、-20、+40 mm，由此可知，适当的欠超高可减缓外轨侧轮轨磨耗，适当的过超高可减缓内轨侧轮轨磨耗，但考虑到曲线外轨侧磨耗更为严重，且随着欠超高的增大，内、外轨磨耗差值减小。因此，设置适当的欠超高更有利于降低轮对磨耗，促使内外轨均磨。

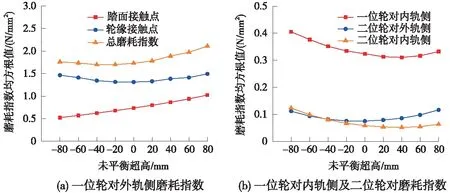
图8 不同未平衡超高对40 t轴重货车轮轨磨耗的影响

图9为惰行工况下，不同未平衡超高对圆曲线段外轨侧钢轨损伤分布情况的影响。对比各未平衡超高下的钢轨损伤情况可看出，随着曲线超高的增加，外轨侧钢轨疲劳损伤区域无明显变化，均位于轨顶面靠近轨距角处，但疲劳损伤幅值显著增大，即过超高状态更容易造成滚动接触疲劳。这主要是因为在欠超高状态下，轮轨冲角较小，且二位轮对贴靠曲线外轨，能够起到一定的导向作用，因而此时一位轮对外轨侧轮轨纵、横向蠕滑率也较小，随着未平衡超高的增加，轮轨冲角增大，二位轮对导向能力降低，使得纵、横向蠕滑率呈线性增加趋势，进而加大了钢轨疲劳损伤的风险。