高速铁路纵连式轨道板空间位移作用下锚固销钉受力特性分析

2021-09-26肖杰灵杨荣山刘学毅

铁道标准设计 2021年9期

袁博,肖杰灵,陈醉,杨荣山,刘浩,刘学毅

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031； 2.西南交通大学土木工程学院，成都 610031； 3.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081)

CRTSⅡ型板式无砟轨道(以下简称“Ⅱ型板”)是一种典型的纵连式轨道结构，因具有高平顺性、高舒适性等优点被广泛应用于我国高速铁路中[1]。由于沿线路纵向连续铺设，温度荷载作用下轨道结构的纵向变形受到约束，产生较大的温度内力，进而引发轨道板上拱、砂浆层离缝、宽窄接缝破损等病害；其中轨道板上拱病害是Ⅱ型板目前最为突出的病害，影响轨道结构稳定性、耐久性和线路平顺性，给线路正常运营带来安全隐患[2]，如图1 所示。销钉锚固限位技术近年来被广泛应用于混凝土结构改造、扩建、加固和维修中[3]。该技术在保证锚固和限位效果的前提下，具有性价比高、灵活高效和施工简便等优势，已成为上拱问题最主要的整治措施之一。

图1 轨道板上拱病害

针对轨道板上拱的整治措施，谭社会[4]利用有限元方法分析了植筋锚固和注胶对轨道板离缝上拱的整治效果，对整治方案进行优化并提出预防措施，为无砟轨道结构病害的养护维修提供参考。景璞等[5]总结调研了Ⅱ型轨道板的各类病害及整治措施，包括上拱离缝病害，并对整治效果进行了验证与对比，提出了病害整治方案。肖春明[6]针对“注胶-植筋”方案，通过Ⅱ型板的现场监测，确认了“注胶-植筋”具有良好整治效果。高睿[7]建立了桥上Ⅱ型板分析模型，研究了植筋注胶措施对轨道结构纵向受力特点的影响。上述研究表明“注胶-植筋”可以有效改善轨道板上拱问题，为轨道板上拱整治措施的进一步研究和优化改进提供了理论基础。现场锚固销钉可以有效抑制轨道板上拱，但销钉存在失效可能，影响整治效果。

针对销钉锚固限位技术方面的研究，德国学者Dr.Jakob Kunz 等[8]进行了后锚固植筋抗火性能试验，得到植筋系统锚固性能与环境温度的关系，并给出了不同锚固条件下植筋承载力计算方法。Miroslav Bajer[9]等研究了粘结锚杆胶-混凝土界面在受拉荷载作用下的反应，给出了组合式混凝土粘结破坏模式下粘结锚受拉荷载下的承载力计算公式。Cook R. A.等[10-12]推导出不同破坏形式下(包括混凝土锥体破坏，粘结破坏，锥体-粘结复合型破坏)锚栓承载力计算公式，并分析了锚固深度对破坏形式的影响。郑晓芬等[13]为探究植筋胶与混凝土之间的界面结合性能，设计了混凝土植筋挤压试验方案，得到了三阶段模式的植筋胶-混凝土界面粘结滑移本构关系。上述研究主要采用了试验的方法，重点关注了锚固销钉的粘结-滑移作用，解决了高温下销钉粘结滑移的力学性能分析，但对锚固销钉及其周围结构的局部受力分析尚需深入研究。

锚固销钉可有效抑制轨道板垂向上拱和纵向错动，但在温度及列车荷载的作用下，轨道板上拱病害可能反复发生，在垂向和纵向位移的作用下，销钉周围混凝土会产生局部应力集中现象[14]，轨道结构和植筋胶存在破坏的风险，同时对轨道板纵向错动的约束减弱。植筋胶具有强度高、粘结力强、固化快、操作简单等优点[15]，利用自身锁键握紧力作用，固化后将销钉与基材粘接为一体，在锚固限位中起着重要的作用[16]。但其弹性模量等刚度特性对整治效果的影响仍需深入研究，销钉锚固限位中规格尺寸的合理选取仍有待商榷。因此，深入探讨位移作用下锚固销钉及轨道局部受力特性对上拱病害的整治具有重要意义。为了分析位移影响下销钉及轨道局部受力特性，通过有限元法对锚固销钉及轨道局部进行力学仿真计算，分析销钉、植筋胶等部件参数对销钉及轨道局部受力的影响，并提出合理的销钉选取方案，为现场销钉布置和后续理论研究提供参考依据。

1 锚固销钉限位分析模型

1.1 计算模型

根据Ⅱ型板的结构特性[17]，建立包括轨道板、CA砂浆层、支承层的锚固销钉局部力学分析模型，如图2所示，并作如下假定。

图2 销钉锚固限位轨道结构及力学图示

(1)受温度、水及列车荷载等多场耦合荷载共同影响，砂浆层与轨道板粘结作用大幅度降低，故不考虑砂浆层对轨道板的粘结强度。

(2)忽略销钉与混凝土之间的滑移性能，植筋胶与销钉、混凝土间仅做线性粘结处理。

(3)钢轨自重与抗弯刚度、扣件系统对轨道板结构形变能影响较小，故不考虑钢轨及扣件对轨道板的影响。

轨道板、支承层、植筋胶和销钉均采用8节点实体单元进行模拟，模型长度为1 m，如图3所示。基于轨道板脱空假定，砂浆层采用非线性弹簧进行模拟，其约束作用满足单向受压弹簧的力学特性，板下砂浆层垂向力-位移曲线如图4所示；路基支承作用采用线性弹簧模拟；为了提高计算效率，模型均简化为线弹性材料。路基底部和底座板端部采用固定约束。通过对轨道板整体施加垂向、纵向位移荷载来分析销钉及轨道局部受力特性。

图3 销钉锚固局部有限元模型

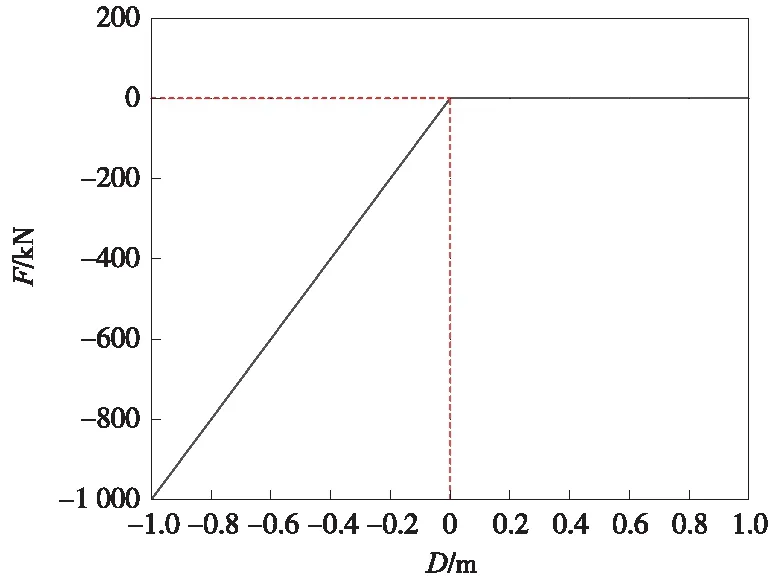
图4 板下砂浆层垂向力-位移曲线

基于上述方法，通过分析位移影响下销钉、植筋胶及轨道板的应力分布特性，讨论销钉直径、植筋胶弹性模量、钻孔直径等因素对销钉及轨道局部受力特性的影响。

1.2 模型参数(表1)

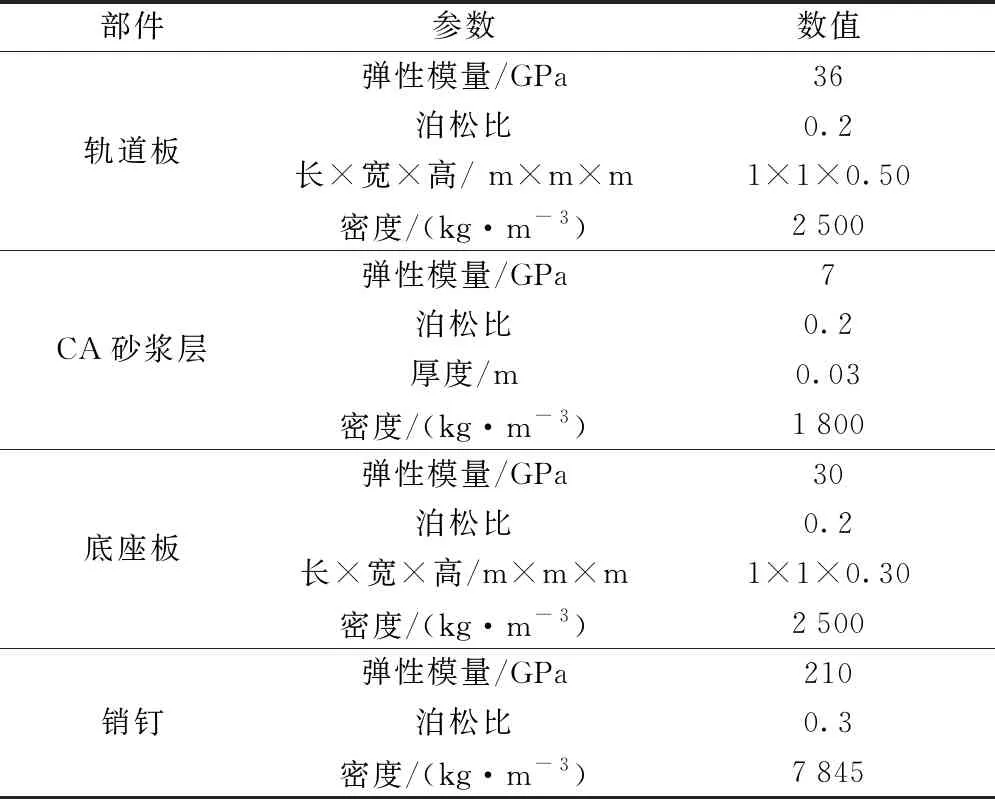
表1 计算模型相关参数

2 锚固销钉受力特性

为研究销钉及轨道局部受力特性，根据现场销钉布设方式，假定选用HRB500级φ28 mm销钉和φ35 mm钻孔。《高速铁路无砟轨道线路维修规则》规定，轨道板最大允许上拱度8 mm，综合现场轨道板上拱情况，故取轨道板上拱0.5～7 mm的情况进行深入研究。分别计算结构在轨道板垂向、纵向位移为 0.5～7 mm时销钉及轨道结构受力情况，计算结果如图5、图6所示。

图5和图6表明，销钉和植筋胶所受拉应力均随轨道板垂向位移呈线性增长趋势，轨道板最大压应力和植筋胶最大剪应力均随轨道板纵向位移呈线性增长趋势。当轨道板垂向发生6 mm位移时，销钉最大拉应力为621 MPa，超过销钉的极限抗拉强度540 MPa，存在受拉破坏的风险；当轨道板发生纵向4 mm位移时，轨道板最大压应力为48.7 MPa，超过混凝土极限抗压强度37 MPa，存在受压破坏的风险；当轨道板发生纵向0.5 mm位移时，植筋胶最大剪应力为35.1 MPa，超过植筋胶极限抗剪强度26.6 MPa，植筋胶抗剪能力较弱。轨道板发生5 mm以上垂向位移和3 mm以上纵向位移时，销钉失效。因此，在保证结构受力状态的前提下，现场选取φ28 mm的销钉，φ35 mm钻孔，植筋胶弹性模量为混凝土的1/10较为合理。

图5 垂向位移作用下销钉和植筋胶最大拉应力

图6 纵向位移作用下轨道板最大压应力和植筋胶最大剪应力

3 销钉直径对销钉受力特性的影响

为研究销钉直径对销钉及轨道局部受力特性的影响，现假定植筋胶弹性模量及钻孔直径不变，根据现有钢筋的公称直径[18]，选取φ20 mm、φ25 mm、φ28 mm、φ32 mm 和φ36 mm五种规格的销钉，分别计算结构在轨道板垂向、纵向位移为0.5～7 mm时销钉及相关结构受力情况。在垂向位移的影响下，销钉和植筋胶存在受拉破坏风险，故选取销钉及植筋胶的最大拉应力为判断依据；在纵向位移的影响下，轨道板局部及植筋胶存在受压破坏的风险，故选取轨道板压应力和植筋胶剪应力为判断依据，计算结果如图7、图8所示。

图7(a)和图7(b)表明，在轨道板产生垂向上拱位移时，销钉所受最大拉应力随其直径的增大而减小；当轨道板垂向位移为7 mm时，销钉最大拉应力由1 320 MPa减少至456 MPa，降低了65.5%。植筋胶所受拉应力亦随销钉直径的增大而减小；当垂向位移为7 mm时，植筋胶最大拉应力由78.4 MPa减少至34 MPa，降低了56.6%。图8表明，当销钉直径为φ20 mm时，轨道板垂向位移超过3 mm，销钉即存在受拉破坏风险；当销钉直径φ32 mm以上时，轨道板垂向位移超过7 mm，销钉才存在受拉破坏风险。为确保极限上拱条件下的销钉应用安全，直径不宜小于φ32 mm。

图7 不同销钉直径下各部件的受力

图8 不同销钉直径销钉失效位移限值

图7(c)和图7(d)表明，在轨道板产生纵向相对位移时，板内最大压应力随销钉直径的增大而增大；当轨道板纵向位移为7 mm时，轨道板最大压应力由54.5 MPa增大至93.9 MPa，增加了42.0%。植筋胶所受最大剪应力亦随销钉直径的增大而增大；当纵向位移为7 mm时，植筋胶最大剪应力由357 MPa增大至494 MPa，增加了38.4%。图8表明，当销钉直径为φ20 mm时，轨道板纵向位移超过4.5 mm，轨道板才存在受压破坏风险；当销钉直径为φ36 mm时，轨道板纵向位移超过3 mm，轨道板即存在受压破坏风险，销钉失效对应的纵向位移限值随销钉直径的增大而减小。当销钉直径为φ28 mm或φ32 mm时，其对应的垂向、纵向位移限值之比接近1，因此，为保证销钉具有良好的受力性能，现场锚固销钉直径宜选用φ28 mm或φ32 mm，并限制轨道板的垂、纵向位移不超过7 mm和4 mm。

4 植筋胶对销钉受力特性的影响

为研究植筋胶弹性模量对销钉及轨道局部受力特性的影响，现假定销钉半径及钻孔半径不变，植筋胶与轨道板弹性模量的比值定为k，根据现有无机植筋胶的弹性模量范围[19]，分别选取k为1/10、1/6、2/6、3/6、4/6和5/6，分别计算结构在轨道板垂向、纵向位移为0.5～7 mm时销钉及相关结构受力情况，计算结果如图9、图10所示。

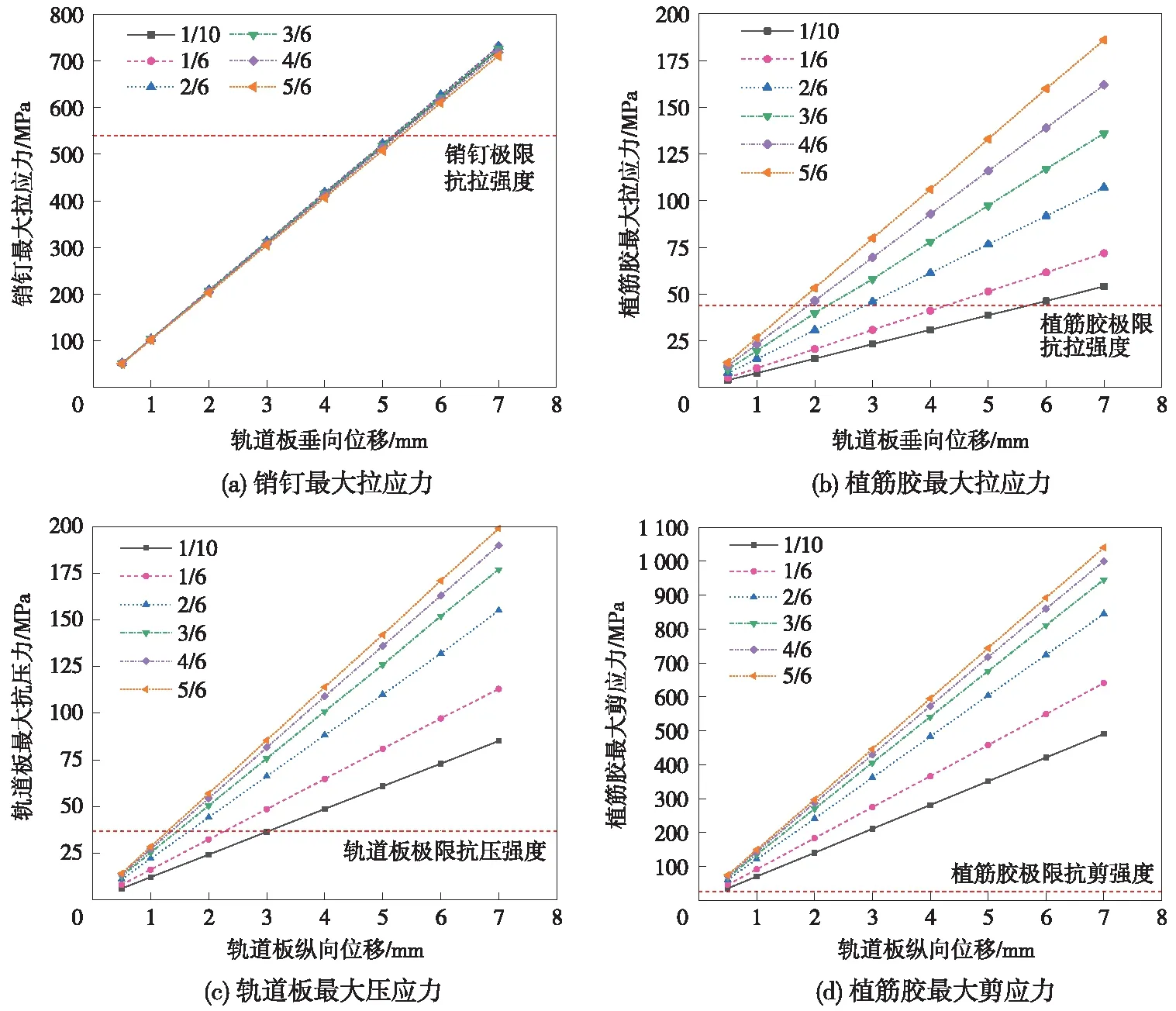
图9 不同植筋胶弹性模量下各部件的受力

图9(a)和图9(b)表明，在轨道板产生垂向上拱位移时，植筋胶弹性模量对销钉受力影响较小；当轨道板垂向位移为7 mm时，销钉最大拉应力由725 MPa减少至711 MPa，降低1%，基本不发生变化。植筋胶所受拉应力随k的增大而增大；当轨道板垂向位移为7 mm时，植筋胶最大拉应力由54.1 MPa增加至186 MPa，增加71%。图10表明，当k=1/10时，轨道板垂向位移超过6 mm时，销钉才存在受拉破坏风险；当k=5/6时，轨道板垂向位移超过1.5 mm时，植筋胶即存在受拉破坏风险。为确保销钉应用安全，植筋胶弹性模量不宜过大。

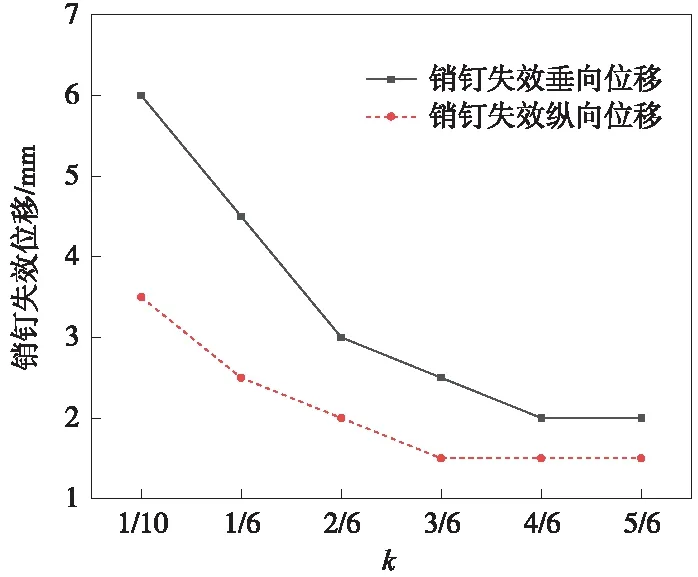
图10 不同植筋胶弹性模量销钉失效位移限值

图9(c)表明，在轨道板产生纵向相对位移时，板内最大压应力随k的增大而增大；当轨道板纵向位移为7 mm时，轨道板最大压应力由85.2 MPa增大至199 MPa，增加了57.2%。图9(d)表明，植筋胶所受最大剪应力随k的增大而增大，当纵向位移为7 mm时，植筋胶最大剪应力由491 MPa增大至1 040 MPa，增加了52.8%。图10表明，当k=1/10时，轨道板纵向位移超过3.5 mm时，轨道板才存在受压破坏的风险；当k=5/6时，轨道板纵向位移超过1.5 mm时，轨道板即存在受压破坏的风险，销钉失效对应的纵向位移限值随植筋胶弹性模量的增大而减小。为保证销钉具有良好的限位效果，现场建议选用植筋胶与轨道板弹性模量之比≤1/10的植筋胶，并限制轨道板的垂、纵向位移不超过6 mm和3.5 mm。

5 钻孔直径对销钉受力特性的影响

为研究钻孔直径对销钉及轨道局部受力特性的影响，现假定销钉直径及植筋胶弹性模量不变，钻孔直径与销钉直径的比值定为t，根据现有施工办法，分别选取t为1.1、1.25、1.45、1.60、1.80、1.95，分别计算结构在轨道板垂向、纵向位移为0.5～7 mm时销钉及相关结构受力情况，计算结果如图11、图12所示。

图11 不同钻孔直径下各部件的受力

图11(a)和图11(b)表明，在轨道板产生垂向上拱位移时，销钉所受最大拉应力随t的增大而减小，但增长趋势较为缓慢。当轨道板垂向位移为7 mm时，销钉最大拉应力由739 MPa减少至571 MPa，降低22.7%。植筋胶所受拉应力随t的增大而增大；当轨道板垂向位移为7 mm时，植筋胶最大拉应力由34.7 MPa增加至75.3 MPa，增加54%。图12表明，当t为1.1时，轨道板垂向位移超过5.5 mm时，销钉才存在受拉破坏风险；当t为1.95时，轨道板垂向位移超过5 mm时，植筋胶即存在受拉破坏风险。为确保销钉应用安全，钻孔直径不宜过小。

图11(c)和图11(d)表明，在轨道板产生纵向位移时，板内所受最大压应力随t的增大而减小，但从t为1.25起减小趋势较为缓慢。当轨道板纵向位移为7 mm时，轨道板最大压应力由116 MPa减小至69.4 MPa，减少了40.2%。植筋胶所受最大剪应力亦随t的增大而减小，当轨道板纵向位移为7 mm时，植筋胶最大剪应力由924 MPa减小至191 MPa，减小了79.3%。图12表明，当t为1.1时，轨道板纵向位移超过3 mm，轨道板即存在受压破坏风险；当t为1.95时，轨道板纵向位移超过4 mm时，轨道板才存在受压破坏风险，销钉失效对应的纵向位移限值随t的增大而增大。当t≥1.25时，销钉失效垂向和纵向位移限值之比相同，为保证销钉具有良好限位效果和考虑经济效益，现场建议选用钻孔半径为销钉直径的1.25倍，并限制轨道板的垂、纵向位移不超过5 mm和4 mm。