钢筋混凝土桁架拱桥承载力加固的力学性能对比分析
2021-09-26王勤征张华刚陈红鸟马克俭魏艳辉
王勤征,张华刚*,陈红鸟,马克俭,魏艳辉,刘 宇
(1.贵州大学 空间结构研究中心,贵州 贵阳 550025;2.贵州省结构工程重点实验室,贵州 贵阳 550025;3.贵州省交通规划勘察设计研究院股份有限公司,贵州 贵阳 550001)
钢筋混凝土桁架拱桥具有结构轻巧美观、受力合理、施工简便、节约材料等优点,因此,20世纪60~70年代在我国得到了迅速发展,尤其在西部山区的交通运输中发挥了重要作用[1]。但随着使用年限的增加、管理维护的不足、交通量的大幅攀升及较多超载现象的出现,大量的桁架拱桥出现了不同程度的病害,主要表现为:①桁架杆件出现横向或环状裂纹,严重者裂纹甚至延伸至节点区域;②横向联结系开裂或断开;③桥面板区域性开裂、破碎,导致路面沉陷;④伸缩缝局部或整体破坏,并延伸至两边桥面;⑤人行道变形、下垂甚至断裂;⑥桥台出现横向或竖向裂缝;⑦结构的部分混凝土剥落、钢筋锈蚀[1-3]。对这些病害不做处理,将会使越来越多的桁架拱桥成为危桥。目前,钢筋混凝土桁架拱桥的加固方法主要有粘贴钢板(或其他高强材料)、增大截面、置换混凝土、转换箱型截面、体外预应力加固和释能法加固等[4-6]。各种加固方法针对的病害类型、加固部位不同,难易程度和加固效果也不尽相同,这就为加固方案的选择带来了困扰。
加固后结构的力学性能是评估加固效果[7]的直观指标,因此,有必要就常用的加固方法做数值模拟。为了解决原桥承载力不足的问题,本文对粘贴钢板、全部截面箱型转换和关键截面箱型转换这3种加固方案,采用Midas/Civil和有限元分析(finite element analysis,FEA)软件对某桁架桥做加固分析,并对比其静力、动力和稳定性等加固效果,以期为同类桥梁的加固提供参考。
1 数值模型
1.1 加固前模型
结合某实际工程,采用一般梁单元和板单元来建立结构的数值分析模型。
桥跨L=35 m,矢跨比为1/7,桥面宽9.5 m,全桥由4片间距为2.5 m的桁架拱片组成,拱片厚度均为35 cm,跨中高度为85 cm,下弦杆厚42 cm,上弦杆厚40 cm。实腹段长11 m,两边空腹段对称布置4个节间,由端部到跨中节间距离依次为4、3、3、2 m,腹杆厚度均为30 cm。横隔板设置4道,厚度均为20 cm。拉杆和剪刀撑截面均为20 cm×20 cm,其中,剪刀撑设在桥两端、L/4和3L/4截面附近对应拉杆处,横系梁截面尺寸为42 cm×20 cm,与竖杆同截面布置。结构的空间示意图如图1(a)所示。

图1 加固前结构模型Fig.1 Structural model before reinforcement
模型全部材料均为C35混凝土,除桥面板外,沿桥梁纵向有限单元的长度均为1 m,共划分了440个单元,348个节点。有限元模型如图1(b)所示。拱脚两端固结,桥面板与上弦杆通过软件弹性连接(刚性)施加约束。荷载由恒荷载(自重、二期恒载)和汽车荷载(汽车正载和偏载)组成,二期恒载满布在桥面板上,大小为2.5 kN/m2,汽车荷载取公路-Ⅰ级,正载和偏载均两车道。模型设置3个施工阶段进行分析,即成桥阶段、二期恒载施加阶段和收缩徐变阶段。
1.2 加固后模型
本文采用粘贴钢板法、全部截面箱型转换和关键截面箱型转换(前者的延伸)对原桥下弦杆进行加固处理来提高其承载力,加固后的结构模型在约束、荷载和施工阶段等方面与加固前相同。
1.2.1粘贴钢板加固模型
通过Midas/Civil软件中施工阶段联合截面将钢板添加在下弦杆上。添加时主要根据两截面形心的相对坐标来确定加固具体位置,加固钢板采用Q235钢,厚度取为8 mm。加固模型如图2所示。
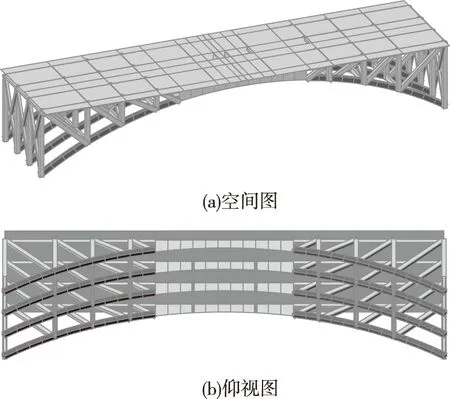
图2 粘贴钢板加固模型Fig.2 Model of pasting steel plate
1.2.2全部截面箱型转换加固模型
在下弦杆的顶面和底面,以及实腹段底面各增设一层钢筋混凝土,由此顶、底两层钢筋混凝土与下弦杆一起构成箱型截面。实腹段处,新增设的钢筋混凝土与实腹段、桥面板也一起组成了箱型截面,而箱内原有的横隔板、拉杆、剪刀撑等横向联结系对截面又起到了加强作用。新增板单元厚度为10 cm,数值模型如图3所示。模型建立时,新增板单元从Midas/FEA导入到Midas/Civil模型中,下弦板单元模型如图3(c)所示。
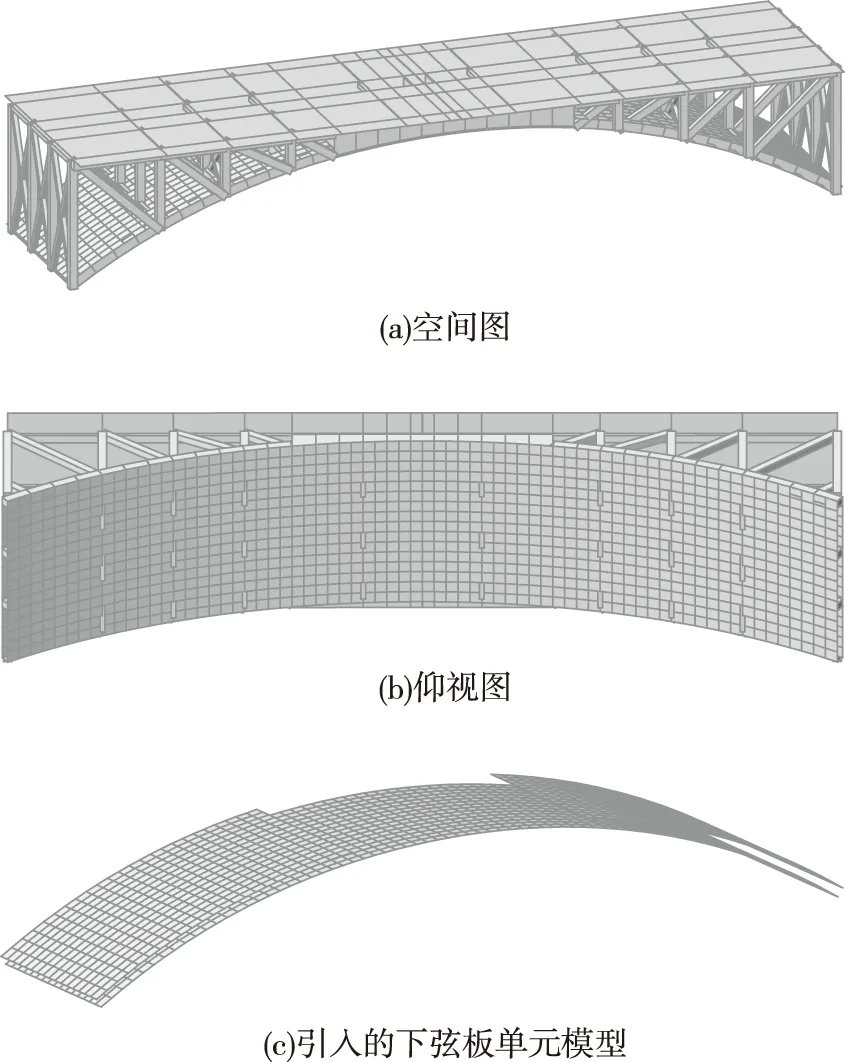
图3 全部截面箱型转换加固模型Fig.3 Model of box transfer reinforcement of all sections
1.2.3关键截面箱型转换加固模型
为了避免全部截面转换加固会引入较大自重的不足,又能将原桥下弦杆联结节点部位加强,本文提出只对下弦杆关键截面处进行箱型转换加固的方法。在竖杆左右两侧(端部竖杆只在桥内侧增设)各1 m宽度范围及实腹段下缘增设10 cm厚钢筋混凝土层,有限元模型如图4所示。
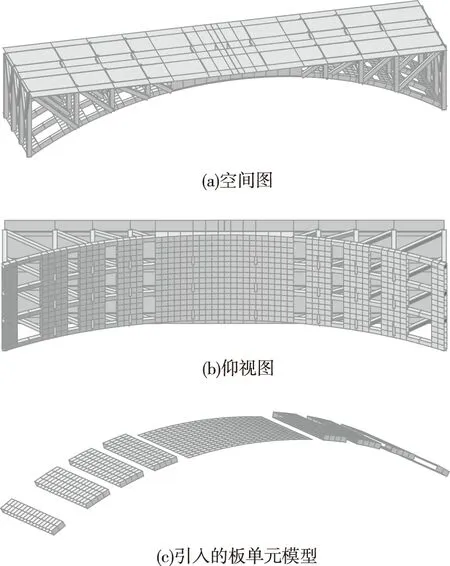
图4 关键截面箱型转换加固模型Fig.4 Model of box transfer reinforcement of key sections
2 力学性能对比分析
本文从加固前后静力、动力和稳定性等3个方面进行对比分析以评价加固效果。
2.1 静力效应
在相同外荷载作用下,提取加固前后不同模型3号拱片的拱脚和跨中截面内力,以及拱圈位移做对比分析。
2.1.1工况及荷载效应组合
根据《公路桥涵设计通用规范》JTG D60—2015的规定,选取了2个荷载组合来进行对比[8]:
1)承载能力极限状态基本组合
Sud=γ0S(1.2Gk+1.4Q1k+0.75×1.4Q2k)
(1)
2)正常使用极限状态作用频遇组合
Sfd=S(Gk+0.7Q1k+Q2k)
(2)
式中:Sud为承载能力极限状态下作用基本组合的效应设计值;S(·)为作用组合的效应函数;γ0为结构重要性系数,取值为1.1;Gk为永久作用(结构重力)的标准值;Q1k为汽车荷载作用效应的标准值,按公路-Ⅰ级车道荷载确定,均布荷载为qk=10.5 kN/m,集中荷载为Pk=330 kN;Q2k为人群荷载标准值;Sfd为作用频遇组合的效应设计值。
车行道宽度为8 m,双向两车道,按照正载和偏载两种工况加载[9],加载布置如图5所示。

图5 汽车荷载加载示意图Fig.5 Schematic diagram of vehicle load
2.1.2内力
正载和偏载工况下,各模型3号拱片下弦杆拱脚截面及跨中截面的内力结果分别见表1~4。

表1 正载工况下各模型拱脚截面内力Tab.1 Internal forces of arch foot section of all models under symmetrical load condition

表2 正载工况下各模型跨中截面内力Tab.2 Internal forces of mid-span section of all models under symmetrical load condition
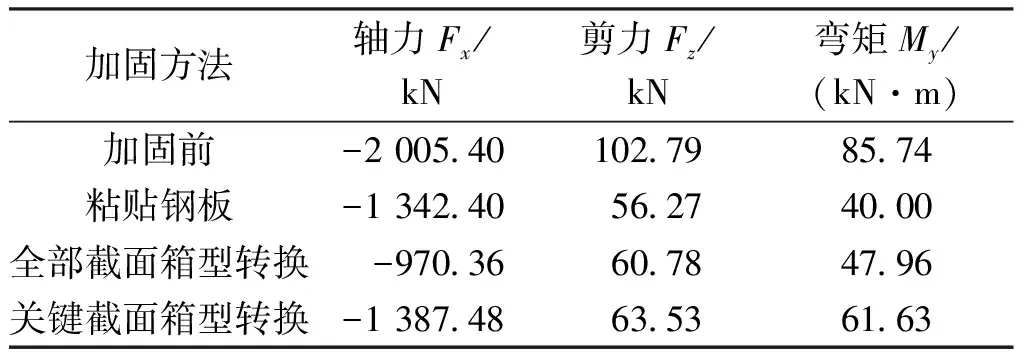
表3 偏载工况下各模型拱脚截面内力Tab.3 Internal forces of arch foot section of all models under asymmetrical load condition
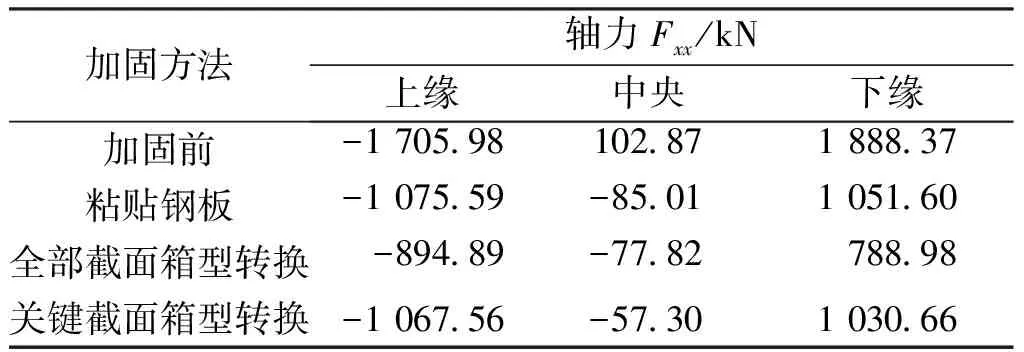
表4 偏载工况下各模型跨中截面内力Tab.4 Internal forces of mid-span section of all models under asymmetrical load condition
由表1~4可见,3种加固方法均可明显降低原结构内力,改善结构承载效果。对于拱脚截面轴力,全部截面箱型转换加固后降为加固前的50%以下,另外两种方法也降为加固前的70%左右;而对拱脚剪力和弯矩来说,截面箱型转换(包括全部截面箱型转换和关键截面箱型转换,下同)加固相比粘贴钢板加固不具备优势,这是由于引入自重明显不同。在正载和偏载两种工况下横向对比,截面箱型转换加固在降低同一截面轴力和剪力时,差值在0.7%~4.3%,而粘贴钢板加固法在两种工况下降低同一截面轴力和剪力的差值分别达到6.4%和6.1%;这说明前者在两种工况下均能较稳定地将荷载分配给4个拱片,相比粘贴钢板加固具有更强的横向联结系和荷载横向分布能力。对于跨中板截面的下缘拉力,全部截面箱型转换加固后同样降为加固前的50%以下,另外两种方法也有明显的降低效果;对于中央位置处的内力,加固后都由拉力转变为压力,说明截面中性轴下移,跨中截面的抗弯刚度得到了大幅度提高,其中以粘贴钢板加固最为明显。
2.1.3竖向位移
正载和偏载工况下,各模型加固前后的竖向位移分布分别如图6~9所示,其中3号拱片下弦杆位移的数值结果如图10所示。
由图10可见:在改善结构竖向变形上,粘贴钢板加固和全部截面箱型转换加固效果相当,均可明显降低桥梁跨中竖向位移,相比加固前跨中位移减少15%~20%;前者在正载工况下略显优势,后者在偏载工况下略显优势,这是因为粘贴钢板加固引入自重较少,而全部截面箱型转换加固引入自重较大,增加了各拱片的横向联结强度,在偏载作用下横向整体受力更好。关键截面箱型转换加固未形成整体的拱圈,以及自重的增加使得结构下挠变形加剧,相比加固前跨中位移增加了9%左右。

图6 加固前的竖向位移分布 图7 粘贴钢板加固的竖向位移分布 Fig.6 Vertical displacement distribution before Fig.7 Vertical displacement distribution reinforcement of pasting steel plate
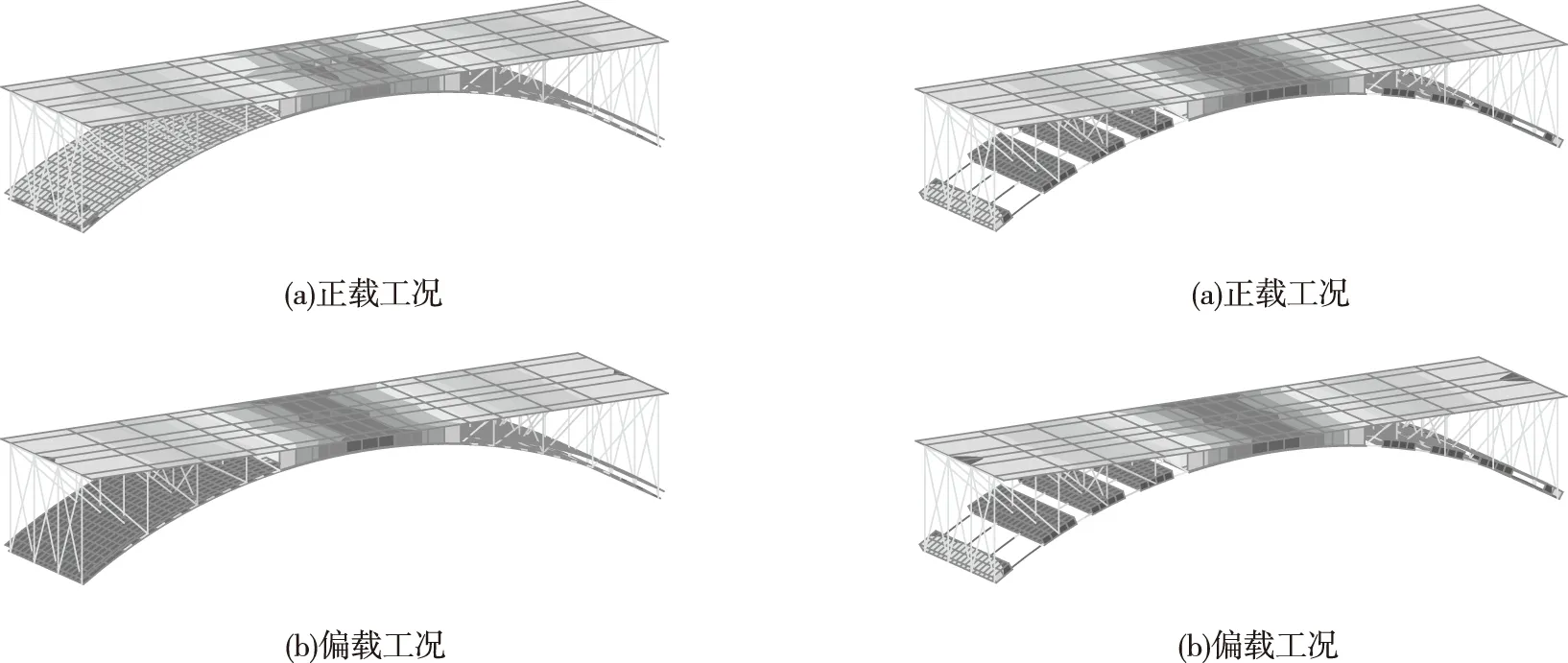
图8 全部截面箱型转换加固的竖向位移分布 图9 关键截面箱型转换加固的竖向位移分布 Fig.8 Vertical displacement distribution of box Fig.9 Vertical displacement distribution of box transfer reinforcement of all sections transfer reinforcement of key sections
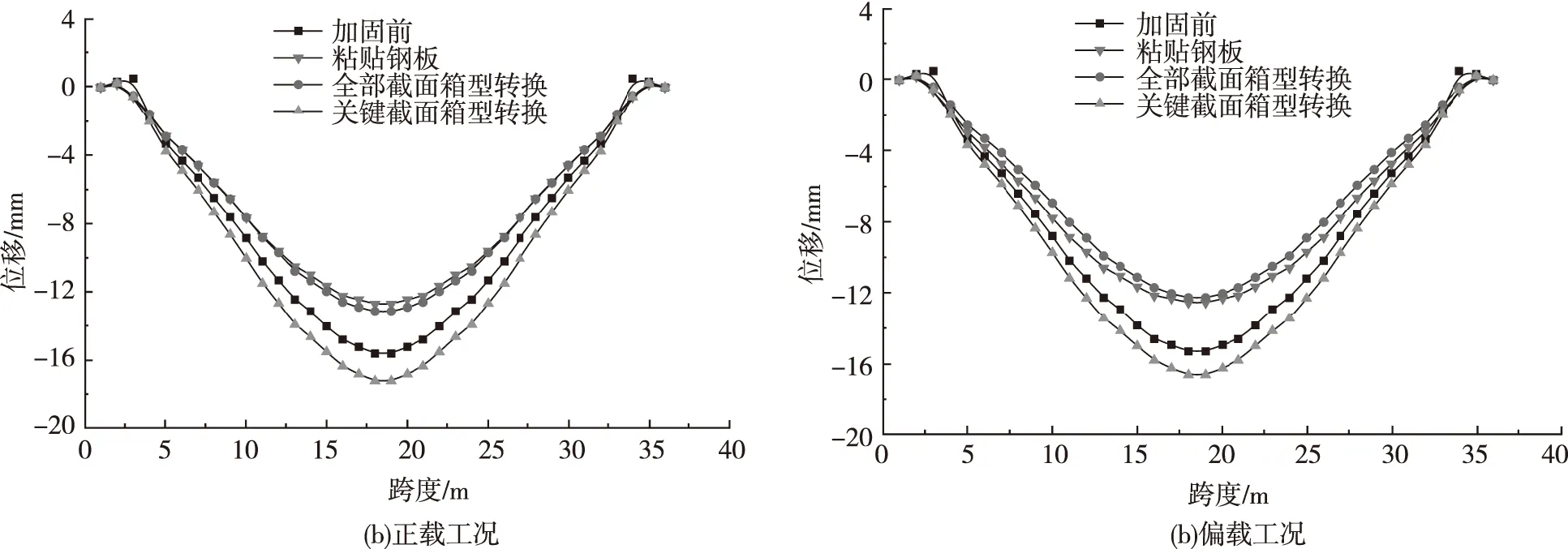
图10 3号拱片下弦杆竖向位移Fig.10 Vertical displacement of lower chord of No.3 arch
2.2 动力效应
基于自振计算结果评估结构加固前后的动力效应[10]。结构的前5阶自振频率结果见表5,对应振型如图11~14所示。

表5 结构的前5阶自振频率 单位:Hz
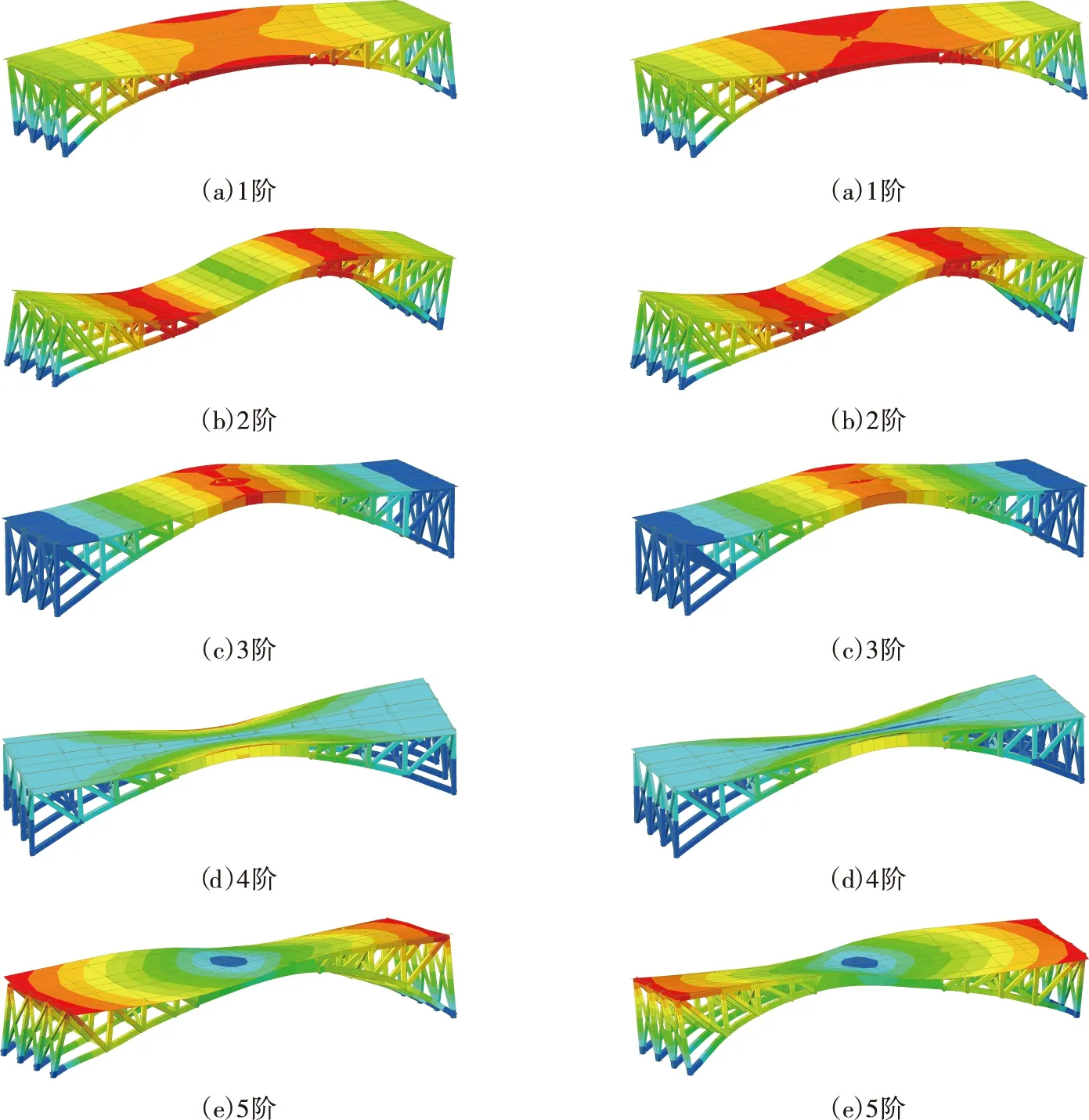
图11 加固前振型Fig.11 Vibration modes before reinforcement

图12 粘贴钢板加固的振型Fig.12 Vibration modes of pasting steel plate

图13 全部截面箱型转换加固的振型Fig.13 Vibration modes of box transfer reinforcement of all sections

图14 关键截面箱型转换加固的振型Fig.14 Vibration modes of box transfer reinforcement of key sections
由表5及图11~14可知:1阶模态下,3种加固方法对结构固有频率都有提高,其中全部截面箱型转换加固最为明显,相比加固前提高了58.1%,同时振型特点由面外转为面内,且前3阶均为面内振动。粘贴钢板加固1阶模态下对结构固有频率影响不明显,主要是由于该方法只加固下弦杆,并未增加拱片间横向联系,横向刚度没有得到明显改变;而2、3阶模态下的竖向刚度有明显提升;4、5阶频率增长平缓,这也是横向联结薄弱所致。关键截面箱型转换加固对结构刚度提升并不理想,主要原因是加固部位分散而未形成整体受力。
2.3 稳定效应
本文的稳定性分析不在于定量追求实际临界荷载的精确性,而在于定性判断加固后结构稳定性的提高效果,所以加固前后均只做线性屈曲分析[11],且各模型初始荷载保持一致,其中,初始恒荷载为自重,初始活荷载为二期恒载。屈曲荷载由临界荷载系数乘以初始活荷载后,再叠加自重得到。用加固前后结构面内和面外1阶屈曲临界荷载系数来比较加固效果,结果见表6。

表6 结构加固前后的1阶屈曲临界荷载系数Tab.6 First order buckling critical load factor of structure before and after reinforcement
由表6可见:加固前结构1阶失稳为面外失稳,面内临界荷载系数是面外的2.43倍,粘贴钢板和关键截面箱型转换加固这2种方法未能改变结构面内和面外稳定性的差距。粘贴钢板加固时面内临界荷载系数是面外的2.75倍,而关键截面箱型转换加固是1.78倍,前者对面内稳定性提高较大(面外提高9.5%,面内提高24.0%),后者对面外稳定性提高较大(面外提高47.1%,面内提高8.2%)。全部截面箱型转换加固将结构1阶屈曲由面外转为面内,在获取前50阶屈曲模态时(此时误差为1.740 6×10-7),结构仍未出现面外屈曲,此时临界荷载系数为799.65,由此说明全部截面箱型转换加固对结构的面外稳定性提高十分有利。由于形成了整体的箱型截面,面内稳定性也较另两种方法好。
3 结论
本文只是从力学性能上来对比分析3种加固方法的效果,实际应用时还要考虑工程造价和施工难易程度的影响,综合确定最优加固方案。通过本文分析,可得如下结论:
1)3种加固方法在改善结构受力、提高旧桥承载能力方面都有一定的效果,其中,全部截面箱型转换加固效果最为明显,而关键截面箱型转换与粘贴钢板在加固效果上相当。
2)粘贴钢板和全部截面箱型转换加固都可以明显降低结构竖向位移,与加固前相比,结构竖向位移降低了15%~20%,而关键截面箱型转换加固对结构竖向位移有增无减。
3)基于下弦杆加固的自振分析表明:全部截面箱型转换加固法可明显提高结构面外刚度,并对面内刚度也有较大改善,而另两种方法对结构刚度改善较不明显。
4)全部截面箱型转换加固法可以显著提高原结构面内、面外的稳定性,粘贴钢板加固对面内竖向稳定性提高较大,关键截面箱型转换加固对面外横向稳定性提高较大。
