一种自适应的工业热异常检测方法

谷艳春，孟庆岩，胡 蝶

(1.福建省交通规划设计院有限公司，福建 福州 350004；2.中国科学院空天信息创新研究院，北京 100094)

我国作为世界上最大的发展中国家，目前正处于工业化进程中[1]。工业化水平从1990年的36.1%上升到2011年的41.3%[2-3]，且社科院称2020年基本实现工业化[4]。迅速的工业化给城市生态环境带来了巨大挑战[5-7]，尤其是工业生产排放的大量废热[8-14]，因分布集中，致使工业区形成城市热岛中的热岛的格局[15-17]。因此，准确检测出引起热异常的工厂，对科学规划工业建设、改善城市热环境具有重要意义。

近年来，国内外学者利用遥感技术对工业区的热环境做了较多研究[18-22]，热红外遥感等技术的发展更为其提供了有效的技术手段。常用异常值检测算法主要包括拉依达准则、肖维勒准则、格拉布斯准则和狄克逊准则[23]。对于大样本实验，拉依达准则效果更佳[23]。且因计算简便，应用广泛[24-27]。如GRUBBS等[28]以均值与2倍标准差之和为临界值检测离群异常值、TIETJEN等[29]实验多组异常值检测，证实了均值与2倍标准差之和为临界值的有效性；JIANG等[30]以均值与1.645倍标准差之和为临界值，检测多组离群异常值；宋冬梅等[31]以均值和1.6倍标准差之和为临界值，检测多景地表温度图中的热异常信息；YANG等[25]以均值和1.5倍标准差之和为临界值，检测多景地表温度图中的热异常。但上述方法存在以下问题：1)利用检测到的异常值进行遥感应用和分析，但对检测的异常值的准确性缺乏验证；2)研究中多采用固定标准差倍数，将该方法应用于多时相多空间遥感影像的热异常检测研究时，存在多提或漏提等问题，适应性较低。

为提高多时相多空间遥感影像的热异常检测准确性，本文提出了一种自适应的热异常检测方法(adaptive thermal anomaly detection，Adaptive-TAD)。该方法通过工厂训练样本和标准差倍数训练样本，训练出热异常最佳临界值。同时，本文基于多时相Landsat 8遥感影像，采用辐射传输法反演地表温度[32-38]，以茌平县和四会市两个工业城市为研究区，并结合Google Earth遥感影像对Adaptive-TAD方法检测的结果进行精度验证。

1 研究方法

1.1 研究区

根据《中国中小城市绿皮书2018》中公布的全国综合百强县市，选取以工业为主导产业，且不同地形的研究区作为Adaptive-TAD方法多时相多空间的典型应用与验证案例(图1)。茌平县(36°22′～36°45′N,115°54′～116°24′E)隶属山东省聊城市，北方平原地形的典型区。四会市(23.33°N,112.68°E)隶属广东省肇庆市，是南方山地地形的典型代表。两者均在2018年入围中国中小城市综合实力百强县市。

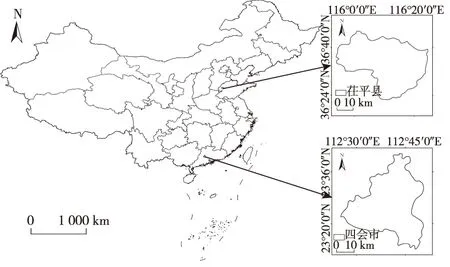
图1 研究区位置示意图Fig.1 The location of the study area

1.2 地表温度反演

传感器接收到的热红外辐射亮度值主要由3部分组成：大气上行辐射亮度值、地面的真实辐射亮度经过大气层后到达卫星传感器的能量、大气下行辐射亮度值(大气向下辐射到达地面后反射的能量)。热红外辐射公式为

Lsensor=[εBTs)+(1-ε)L↓]τ+L↑

(1)

式中，Lsensor是表观辐射亮度；ε是地表比辐射率；Ts是地表温度；BTs是基于普朗克定律得到的黑体在Ts下的辐射亮度；L↓是大气下行辐射；τ是大气透过率；L↑是大气上行辐射。

由式(1)推导出温度为T的黑体在热红外波段的辐射亮度BTs的公式为

(2)

根据普朗克公式的反函数获取地表温度Ts，可将式(2)写为

Ts=K2/ln(K1/BTs+1)

(3)

式中，K1和K2为定标常数，在Landsat 8影像中分别为774.89 W·m-2·sr-1·μm-1和1 321.08 K。

由式(1)、(2)和(3)可知，获取地表温度辐射传输法还需要两类参数：大气剖面参数和地表比辐射率。其中，大气剖面参数L↓、L↑和τ均可在大气计算网页获取(https://atmcorr.gsfc.nasa.gov/)。

VAN等[39]于1993年首次发现在8～14 μm范围内归一化植被指数(NDVI)和地表比辐射率之间有很好的对数关系，提出了VAN半经验公式(4)。因此，本文利用Landsat 8数据的可见光与近红外的光谱信息，计算归一化植被指数(NDVI)，估算地表比辐射率。

ε=1.009 4+0.074×ln(N)

(4)

(5)

式中，N为归一化植被指数(NDVI)，Tnir和Tred分别为Landsat 8影像的近红外波段和红光波段。

地表物质结构虽然较复杂，但从遥感尺度大致可分为3种类型：水体、城镇和自然表面[14]。而水体像元的地表比辐射率很高，与黑体的比辐射率较为相似，因此，在估算水体比辐射率时，常被赋值为0.995[40-42]，自然表面和城镇像元的地表比辐射率估算分别根据式(6)和式(7)计算：

eS=0.962 5+0.061 4P-0.046 1P2

(6)

eB=0.958 9+0.086P-0.067 1P2

(7)

式中，eS为自然表面像元的地表比辐射率，eB为城镇像元的地表比辐射率，P为植被覆盖度。P计算方法如式(8)所示[43-44]：

(8)

式中，N是影像的归一化植被指数(NDVI)，NV和NS分别代表影像中纯植被像元的NDVI值和纯土壤像元的NDVI值。P的取值如式(9)所示[45]，并利用式(8)估算影像的植被覆盖度。

(9)

由于传感器视域外的杂散光引起Band11的定标出现偏差[32-33]，不能用于定量研究[34]，应以TIRS的第10波段的方式来反演地表温度为宜[35]，且对于适合Landsat 8影像地表温度反演的算法中，多个研究者实验证明辐射传输法的适应性较好且应用广泛[36-38]，故本文利用Band10单波段基于辐射传输法反演地表温度。

1.3 工业热异常检测方法

1.3.1Adaptive-TAD方法原理

拉依达准则是由Wright在1884年提出[46-47]，又称3倍标准差准则(3σ准则)。基本思想是，通过计算观测值偏离临界值的程度来判断该观测值是否为异常值。以数据形式解释其基本原理为，存在数据集X={X1，X2，…，Xn}，若某个可疑值Xi与数据集X的均值之差(Xi-μ)的绝对值大于3σ，则认为Xi为异常值，如式(10)和图2。

图2 基于拉依达准则的异常值判定Fig.2 Outlier determination based on PaǔTa criterion

|Xi-μ|>3σ

(10)

式中，μ为数据集的均值，计算公式为式(11)；σ为数据集的标准差，计算公式为式(12)；3σ为拉依达准则的异常值临界值。用c代表临界值，计算公式为式(13)；k为标准差倍数。

(11)

(12)

c=μ+kσ

(13)

1.3.2Adaptive-TAD方法构建

标准差能很好反映每个像元的温度相对于平均温度的偏离程度，结合均值和标准差更能反映不同温度值的变异[48]。以均值和固定成倍标准差之和为临界值进行热异常检测，计算量小，但热异常临界值是随着空间和时间的变化而改变，具有一定的波动性，检测热异常仅以均值和固定成倍标准差之和作为临界值的识别方法往往缺乏应用的适应性。因此，本文构建一种Adaptive-TAD方法，有效地对标准差倍数的变化进行自适应调节。该方法可分为3步(图3)：1)训练工厂样本；2)训练标准差倍数；3)结合工厂训练样本和热异常训练样本，训练出最佳临界值。

图3 Adaptive-TAD方法流程Fig.3 Adaptive-TAD method flow

Adaptive-TAD方法中最核心的是自适应倍数训练，该训练是基于二分法的思想，训练过程如图4所示，sv代表起始值，bv1和bv2代表两个边界值。具体训练步骤为：1)以拉依达准则的3(标准差倍数)为起始值，依据先验知识[49-50]，将1和5设置为边界值，并计算检测热异常结果与研究区内工厂训练样本的重叠度(检测出的热异常与工厂样本的重叠面积大小)；2)若3和5的结果的重叠度较高，则重新以3和5之和的一半为起始值，3和5为边界值，对比三者检测结果的重叠度；3)若3和4的结果的重叠度较高，则比较3、3.5(保留一位小数)和4结果的重叠度；4)若3.5和4的结果的重叠度较高，则比较3.5、3.8和4结果的重叠度；5)若3.5结果的重叠度最高，则3.5为训练出的最佳标准差倍数。起始值与边界值的值距小于0.3时，检测出的热异常结果与研究区内工厂训练样本的重叠度一致。因此，直到边界值与起始值的值距在0.3内，停止训练。

图4 自适应倍数训练流程Fig.4 Adaptive multiple training process

2 结果与分析

2.1 地表温度遥感反演结果与空间分析

利用1.2节的辐射传输法对两个研究区的8景影像进行温度反演，得到地表温度分布图，如图5所示。根据地表温度空间分布格局可以看出，城区地表温度明显高于周边郊区，城区内的工业区地表温度明显高于其他功能区，形成岛中岛的高温区域，且界限清晰。表明工业热异常不仅确实存在，且十分明显。

图5 地表温度反演图Fig.5 Map of LST

2.2 工业热异常遥感检测

2.2.1工业热异常结果对比分析

为了验证Adaptive-TAD方法的有效性，将本文方法与经典的拉依达准则方法(3倍标准差，简称3倍方法)和应用广泛的以均值与1.645倍标准差之和为临界值的方法(简称1.645倍方法)作对比试验。图6展示了1.645倍方法、3倍方法和Adaptive-TAD方法的临界值、像元个数和面积占比对比结果，图7和图8分别展示了3种方法检测热异常结果的整体和局部效果。

从图6(a)可以看出，Adaptive-TAD方法的临界值均大于1.645倍准则的临界值，8景遥感影像的临界值差分别为：4.93、5.12、4.67、2.3、5.47、3.36、4.23、4.37 ℃。表明1.645倍方法检测工业热异常结果会有较多冗余的现象。Adaptive-TAD方法与3倍方法相比，有6景遥感影像数据是Adaptive-TAD法的临界值大，有两景是3倍方法的临界值大，表明3倍方法在同一研究区会有检测结果不一致的可能。从图6(b)可以看出，由于Adaptive-TAD方法的临界值均大于1.645倍方法的临界值，所以基于Adaptive-TAD方法检测的热异常像元数均小于基于1.645倍准则检测的热异常像元数。同时，Adaptive-TAD法检测同一研究区的像元数总体趋于一致，而1.645倍方法和3倍方法检测的像元数一致性较差，这与工厂热异常像元数应趋于一致的实际不符。可见，Adaptive-TAD方法比1.645倍方法和3倍方法对热异常进行检测更具有实际意义。从图6(c)可以看出，3种方法检测的面积占比(检测的热异常面积与研究区面积之比)结果差异较大。具体表现为，Adaptive-TAD方法的面积占比均小于1%且一致。1.645倍方法的面积占比均值为6.47%，甚至高达9.72%，而短时间内研究区的整体工厂规模占比变化应较小，因此1.645倍方法的整体面积占比的一致性较差。3倍方法的面积占比虽冗余较少，但整体结果的一致性较差。综上，Adaptive-TAD方法在同一研究区的参数取值一致性较好，这为提高检测工业热异常的准确性奠定了基础。

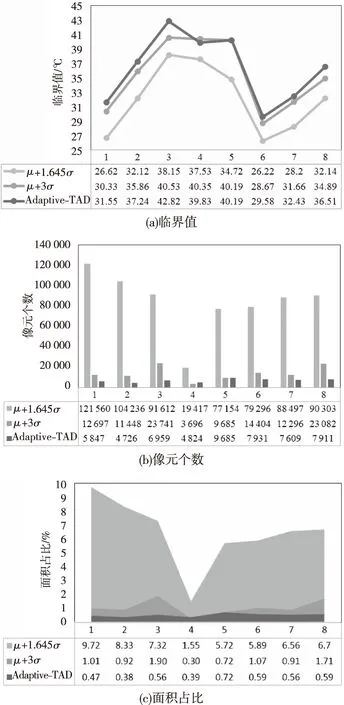
图6 热异常检测参数对比Fig.6 Thermal anomaly detection parameter comparison

从图7可以看出，Adaptive-TAD方法检测工业热异常的整体效果较好，同一研究区的检测结果较为一致；1.645倍方法检测结果中存在较多冗余错误；3倍方法检测结果存在部分遗漏和冗余错误，检测工业热异常结果的一致性较差。图8的局部效果展示的是热异常密集区，以全色波段影像(灰色)为底图叠加检测的热异常结果(红色)。从局部放大图可以看出，Adaptive-TAD方法检测的工业热异常边界与实际工厂轮廓较吻合；1.645倍方法检测的热异常范围与建设用地区域较一致，原因主要是由于该方法的临界值较小，建设用地的地表温度也较高，容易把建设用地当成热异常区错误检测出来；3倍方法检测结果的一致性较低，存在遗漏和冗余问题，原因主要是由于该方法采用固定标准差倍数，适应性较差。总体上，Adaptive-TAD法可以有效地检测出工业热异常，取得了优于1.645倍方法和3倍方法的检测结果。

图7 整体热异常检测结果Fig.7 Overall thermal anomaly test results

图8 局部细节对比Fig.8 Local detail comparison

2.2.2Adaptive-TAD方法精度评价

为定量评价Adaptive-TAD方法的性能，采用生产者精度(producer accuracy,p)、漏提率(leakage probability,l)、用户精度(user accuracy,u)和误提率(error probability,e)作为4个定量评价指标，对本文提出的Adaptive-TAD方法检测的工业热异常的精度进行评价。4个指标的定义如下：

p=St/Sa×100%

(14)

l=(1-St/Sa)×100%

(15)

u=St/Sd×100%

(16)

e=(1-St/Sd)×100%

(17)

式中，St为检测到的正确热异常个数，Sa为实际工厂总个数，Sd为检测到的热异常个数。

采用生产者精度、漏提率、用户精度和误提率4个指标对Adaptive-TAD方法检测工业热异常结果的精度进行评价，得到的结果如表1所示。从表1可以看出，8景遥感影像数据的生产者精度均值为76.54%，最高可达94.97%，用户精度均值为84.44%，最高可达98.11%。其中，茌平县的a景影像中的两个精度均较低，是因为检测的热异常总个数少于实际工厂总个数，同时有部分误提(34.57%)的热异常，即存在非工业生产活动导致的热异常。结合Google Earth影像，发现在误提的热异常中有温度可以达到热异常临界值的蔬菜大棚、未形成规模的工厂和小作坊等。茌平县的d景影像的生产者精度为76.47%，明显低于用户精度98.11%。通过图5(a)的地表温度图可以看出，因西北热异常的消失，致使检测的热异常总个数减少，漏提率高达23.53%，但误提率仅1.89%，表明在检测的热异常结果中较多为工业热异常。四会市的b景影像的生产者精度低至40.39%，漏提率高达59.61%，是因为绥江两岸的工厂较多没有出现热异常现象。但用户精度高达92.48%，表明在检测的热异常中较多为工业热异常，针对工业热异常检测准确度较高。四会市的d景影像数据的生产者精度为94.97%，是8景影像数据中精度最高的，仅有5.03%的漏提率。总体上，本文提出的Adaptive-TAD方法能够比较完整、准确地检测出工业热异常。

表1 研究区基于Adaptive-TAD方法的热异常检测精度统计Tab.1 Thermal anomaly detection accuracy statistics based on Adaptive-TAD method in study area

3 结论

本文提出了一种适用性较强且精度较高的工业热异常检测方法——Adaptive-TAD，该方法的核心是通过工厂训练样本和标准差倍数训练样本，训练出热异常最佳临界值。实验结果表明，Adaptive-TAD方法具有简便、准确、适用性较强等优势，且检测结果明显优于1.645倍方法和3倍方法。具体结论如下：

1)Adaptive-TAD方法可以有效地对不同研究区进行工业热异常检测，并在一定程度上减少漏提或误提现象，表明该方法具有较好的空间普适性。

2)Adaptive-TAD方法能够实现多时相遥感影像的工业热异常检测，且检测精度有大幅度的提高，表明该方法具有较好的时间普适性。

3)基于Adaptive-TAD方法在多空间进行多时相遥感影像的工业热异常检测，生产者精度均值为76.54%，最高可达94.97%，用户精度均值为84.44%，最高可达98.11%。表明该方法检测到的工业热异常与实际工厂热异常一致性较高，可以实现高精度、多空间多时相的工业热异常检测。

Adaptive-TAD方法可实现多空间、多时相、高精度的工业热异常检测，可为工业热异常检测和监测提供技术支撑，研究结果对科学规划工业建设、改善城市热环境具有重要意义。但该方法在每个研究区内需要人工选取工厂训练样本，每景遥感影像均需训练最佳临界值。因此，下一步研究工作的重点是探索无需训练样本的检测方法。