动车所选址和列车开行方案编制协同优化

崔赞扬，张星臣，王志美，陈军华

(北京交通大学 交通运输学院，北京 100044)

在高速铁路运营过程中，动车组的存放与检修始终是运输组织过程中必须要考虑的问题.动车所作为动车组日常存放与检修的场所，其选址问题往往在生产力配置层面考虑.但随着我国高速铁路运营网络规模的快速扩大，先布局生产力，再设计运输产品的研究思路逐渐无法适应高速铁路复杂多变的客流需求.将动车所选址、车站选址等生产力配置层面的问题与开行方案、动车组运用交路等运输产品设计问题联合考虑[1]有助于增强基础设施与运输组织的适应性，提高运营效率.

动车所布局限制了列车运行线的起点和终点，决定了列车的开行距离和空间移动范围，是列车开行方案编制的重要输入之一.而根据列车开行方案所规定的列车的起讫点、运行径路、停站、列车种类、编组、服务频率等信息[2]可以估算出动车组存放与检修的空间需求.因此将动车所选址与列车开行方案编制协同考虑是解决动车所布局问题的重要途径之一.

目前国内外在列车开行方案和动车所选址方面开展了一定工作.在列车开行方案编制方面，付慧伶等[2]构建基于备选集的高速铁路列车开行方案优化模型；周文梁等[3]考虑列车服务水平与旅客出行需求之间的关系，提出面向弹性需求的城际列车开行方案优化模型；Borndörfer等[4]以旅客旅行时间和运行成本为优化目标，建立多商品流模型并采用列生成算法进行求解.在动车所选址方面，王利锋[5]采用相对定性的方法对动车段布局规划提出了建议；钱继磊等[6-7]建立动车组运用检修模型对动车运用所布局方案进行评价，给出合理建议；Canca等[8]提出一种通用的混合整数规划模型，在编制动车组周转计划的同时考虑动车所的位置和数量问题.在二者协同优化方面，姚迪[9]从高速铁路网络能力运用角度建立列车开行方案与动车所布局协同优化模型，虽然在协同优化方面做了探讨，但其未将动车所建设成本考虑在内，对于动车所与列车开行方案的联动关系没有展开研究.

综上，动车所选址与列车开行方案协同优化尚未得到学术界高度关注.随着线网结构加密，客流需求个性化，运输组织模式多样化，采用相对定性或侧重布局方案比选的定量方法对动车所选址问题进行研究时，无法精确反映客流、列流和动车所的联动变化.再者，现有的列车开行方案编制研究因受限于动车所布局条件，其优化空间有限.如京沪线苏州北站，虽然日均上下车客流量很大，由于动车所资源限制，相比同规模客流量车站，从苏州北站出发的始发直达列车数远小于其他车站.

基于以上分析，本文作者将动车所选址与列车开行方案编制进行协同优化，在Karbstein等[10-11]提出的列车开行方案编制模型基础上，以列车开行成本、动车所建设成本和动车组出入动车所空驶成本之和最小为目标，考虑动车所与开行方案关联条件以及动车所数量限制条件，建立混合整数规划模型.根据模型特点设计拉格朗日松弛算法，最后以珠三角城际铁路网络为案例验证了模型与算法的有效性，有效避免了现有研究的不足.

1 数学模型

本文重点研究在给定路网条件、客流OD矩阵、动车所备选点集合条件下的动车所选址与列车开行方案编制协同优化问题.假定：1)旅客基于最短路径出行；2)动车所规模满足动车组存放与检修需求，根据编制的列车开行方案估算动车所规模；3)由于动车所前往其直接关联车站间空驶里程难以估计，暂不做考虑.

1.1 相关定义及符号说明

给定有向网络G=(V,A)，其中V=V1∪V2，V1为铁路车站集合，s,t∈V1为铁路车站索引；V2为备选动车所集合，ξ∈V2为备选动车所索引；A为铁路区间集合，a∈A表示铁路区间索引，其最大通过能力为Ca，区间长度为la≥0，旅行时间为ta≥0.

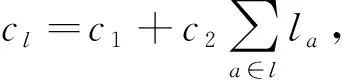
2)客流OD及出行路径备选集.定义D为客流“起点—终点”集合，(s,t)∈D表示一个OD对，其客流需求为dst≥0.旅客从车站s到达车站t的最短路径集合为Pst，P=U(s,t)∈DPst为所有OD对间最短路径集合，Pa∈P为经过铁路区间a的旅客出行最短路径集合.

1.2 主要变量说明

定义xlf为0-1变量，若列车l服务频率为f则取值为1，否则取值为0；yp为整数变量，表示选择路径p出行的旅客数量；zξ为0-1变量，若在ξ设置动车所则取值为1，否则取值为0；wlξ为0-1变量，若选择ξ作为列车l车底存放与检修场所则取值为1，否则为0.

1.3 动车所选址和列车开行方案协同优化模型

所提出的协同优化模型以列车开行成本，动车所建设成本和列车出入动车所空驶成本为优化目标.

目标1：最小化列车开行成本，即

(1)

目标2：最小化动车所建设成本，即

(2)

式中：cξ为在ξ设置动车所的日均成本，根据动车所建设成本、使用年限、年折损率换算得到.

目标3：最小化列车出入动车所空驶成本，即

(3)

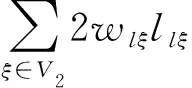
求解多目标问题时可以根据目标函数的重要度设置权重系数ω，将其转换为单目标规划问题，转换后的目标函数为

minz=ω1z1+ω2z2+ω3z3

(4)

模型约束条件如下：

1)任意OD对间的旅客出行路径所分担的客流总量应等于其总的客流量，因此客流路径分配约束为

(5)

2)在任意铁路区间列车所提供的服务能力应大于客流需求，同时为了保证一定的旅客舒适度应将列车上座率控制在一定阈值，因此铁路区间服务能力约束为

(6)

式中：θ为列车上座率.

3)列车l最多只能从备选服务频率集合中选择一种服务频率，或者不选，因此列车服务频率约束为

(7)

4)通过铁路区间a的旅客列车数量不能超过其最大通过能力，因此铁路区间通过能力约束为

(8)

5)承担列车l运行任务的动车组车底需要从动车所中选择一个作为其存放、检修基地，因此动车组车底基地配属约束为

(9)

6)承担列车l运行任务的动车组车底必须从已建动车所中选择一个作为其存放、检修基地，且不能超过动车所的检修能力，因此动车组车底基地配属合理性约束为

≤Mzξ∀ξ∈V2

(10)

式中：M为任意大数.由于暂不考虑动车所能力限制，因此式(10)可简化为

(11)

7)应至少建设1个动车所，至多建设n个动车所，因此动车所设置数量约束为

(12)

2 求解算法

由于所构建的协同优化模型包含优化目标较多，动车所选址与列车开行方案编制相互影响，同时决策变量均为离散正整数，因此该模型是一个不连续、非凸的混合整数规划模型，直接求解难度较大.为了降低求解难度，提高求解效率，设计拉格朗日松弛算法进行求解.通过分析模型结构发现式(6)反映了客流路径分配与列车运输能力之间的关系，以此为界限，可以将其他约束划分为客流约束与列车开行约束.采用拉格朗日松弛技术对式(6)进行松弛并将其作为惩罚项引入目标函数，由此便可得到容易求解的客流路径分配问题和列车开行方案以及动车所选址问题.设计拉格朗日松弛求解算法如下：

1)模型分解，引入拉格朗日乘子λa≥0对式(6)进行松弛得到拉格朗日函数L：

(13)

进一步可改写为

(14)

将拉格朗日松弛问题拆分为关于客流路径分配子问题LR-1，和关于列车开行方案及动车所选址子问题LR-2，其数学模型目标函数分别表达为

(15)

(16)

LR-1约束条件为：客流路径分配约束式(5).

LR-2约束条件为：式(7)～式(9)、式(11)、式(12).

在此基础上通过求解拉格朗日对偶问题LD=maxλa≥0(L)获得原问题的最大下界，对偶问题采用次梯度法求解.

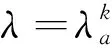
4)记Xk对应原问题目标函数值为Zk，若Zk≤UB，则更新UB=Zk,X*=Xk，否则不更新UB,X*，转第5)步.

5)更新下界，若Lk>LB，则更新LB=Lk.

6)更新拉格朗日乘子，根据式(13)计算乘子λa的次梯度为

(17)

更新拉格朗日乘子

(18)

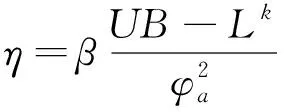
7)当满足终止条件时结束算法，否则令k=k+1，返回第3)步.

3 案例分析

选取珠三角城际铁路网中的1—肇庆，2—佛山西，3—广州南，4—珠海，5—珠海机场，6—广州东，7—新塘，8—望洪，9—虎门，10—深圳，11—惠州等站所构成的城际铁路网络为研究对象，如图1所示.

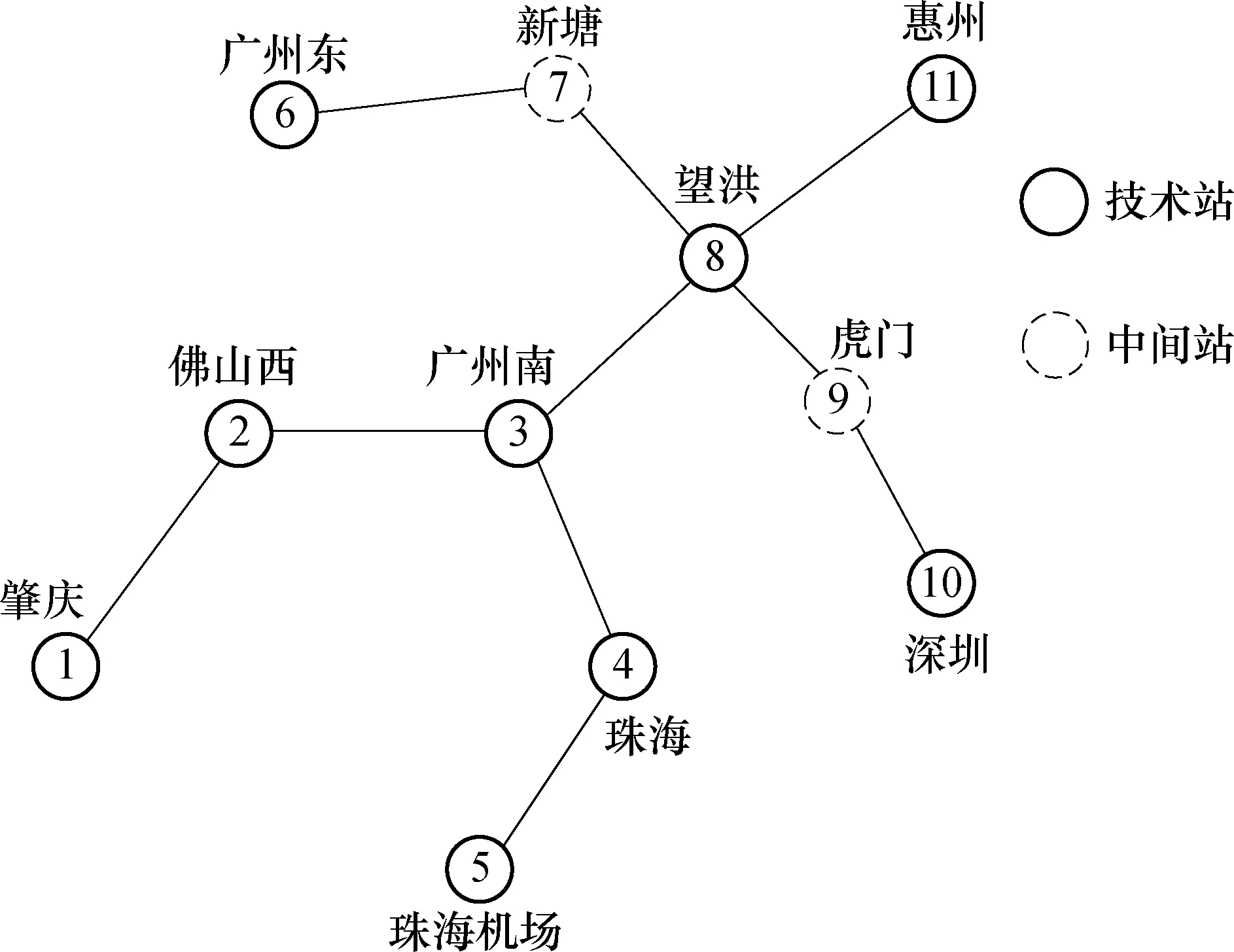
图1 案例网络拓扑图Fig.1 Network topology of case study

图1中,新塘站与虎门站为中间站，其他车站均可办理列车始发终到作业.具体参数设置[9]为：目标函数权重系数取1/3，采用CRH380A-16车型，列车定员1112人/列，各路段间里程及OD客流矩阵详见文献[9]，固定成本30 000元/列，可变成本650元/列·km；动车所建设平均费用约1亿元[12]，使用年限按30 a计，每年折损率为4%[1]，换算为日均费用；动车所与列车始发终到站间的里程根据路段距离计算，动车所与其直接关联车站间的里程不做考虑；以初始方案[9]的目标函数值作为初始上界.采用python3.6实现拉格朗日松弛算法，LR-1和LR-2问题调用Gurobi处理.

首先将动车所设置数量限定在2个以内，上座率设为1，计算结果如表1所示，其中空驶里程均为0.算法收敛过程如图2所示，算法收敛时上下界对偶间隙为17.11%.

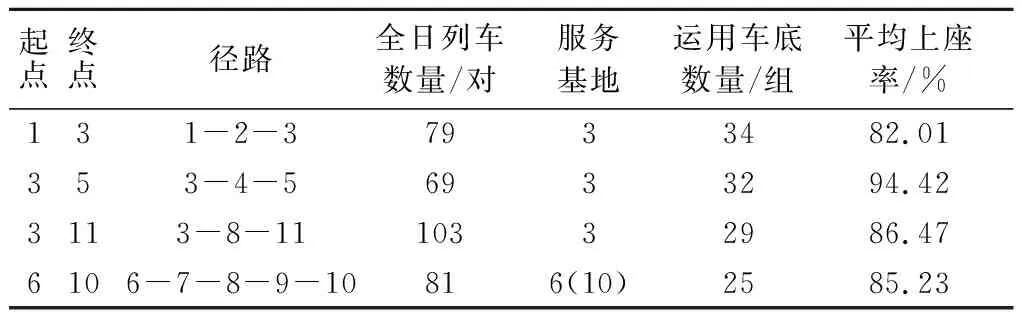
表1 动车所布局及列车开行方案Tab.1 Layout of EMU depot and line planning

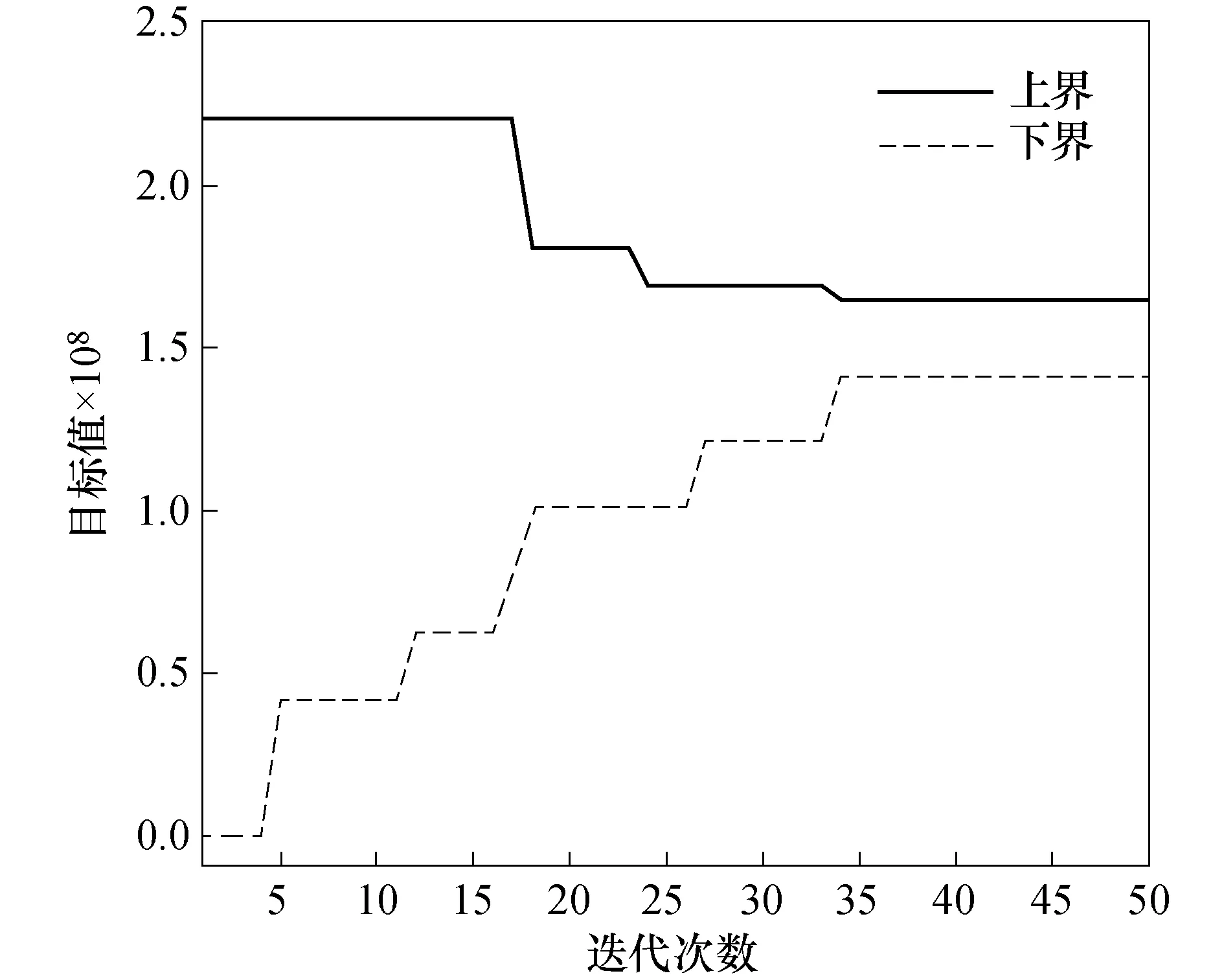
图2 拉格朗日算法收敛过程Fig.2 Convergence process of Lagrange algorithm

通过分析表1可知，优化后原来在站3设置的动车所不变，承担站1与站3间79对列车、站3与站5间69对列车以及站3与站11间103对列车，共计251对列车的存放和检修任务；原来在站6设置的动车所也可不变(也可选择在站10设置动车所)，负责站6与站10间81对列车的存放与检修任务.

将所得优化方案与文献[9]中的原始方案及对比方案进行比较，如表2所示.

通过分析表2可得以下结论：

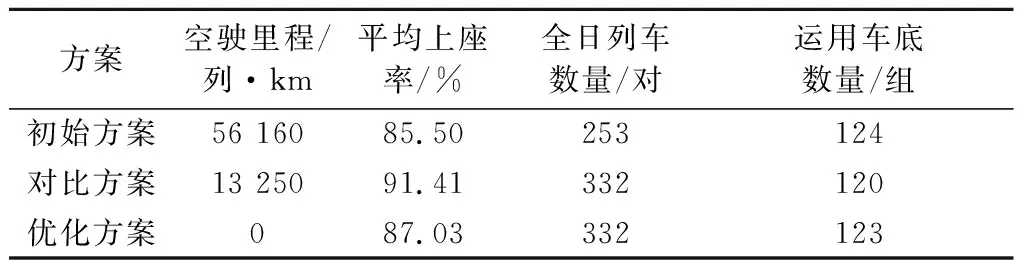
表2 方案对比分析Tab.2 Comparative analysis of different schemes

1)与初始方案相比，所得优化方案在相同运用车底数量条件下开行了更多的列车.这是由于优化方案在客流较大的区段增开了小交路列车，相比初始方案缩短了部分列车的交路长度，减少了客流量较小区段的列车数量，使得列车运能充分利用，即列车平均上座率得到了提升.

2)与对比方案相比，优化方案上座率降低了4.4%.主要是优化方案将对比方案中的站8至站11间开行的旅客列车调整为在站3至站11间开行，增加了站3至站8间运行区段，由于站3至站8间的客流略低于站8至站11间的客流，从平均值上拉低了上座率.其数据的本质是以牺牲部分区段的列车上座率来确保最少的空驶距离.

3)在相同的动车所设置数量和客流数据基础上，在不考虑动车所至其直接关联车站间里程时，因将动车所选址与列车开行方案编制协同优化，与初始方案相比，优化方案中动车组出入动车所产生的空驶里程减少了56 160列·km，与对比方案相比，优化方案中动车组出入动车所产生的空驶里程减少了13 250列·km，显著降低了动车组从动车所至列车始发或终到站间的无效空驶距离.

4)与对比方案相比，优化方案增加了3组车底.主要是优化方案为了确保最少的空驶里程而调整了部分列车运行区段，增加了列车运行交路长度，从而造成运用车底数量的增加.但空驶里程的减少能够显著提高列车运行效率，提供更为合理的列车开行方案，使得旅客享受更为舒适的服务，验证了所提出的模型和方法的有效性和合理性.

为进一步研究动车所选址与列车开行方案的相互影响，将动车所设置数量上限设置为4，列车上座率分别设置为0.8, 0.9, 1.0，求解结果见表3.

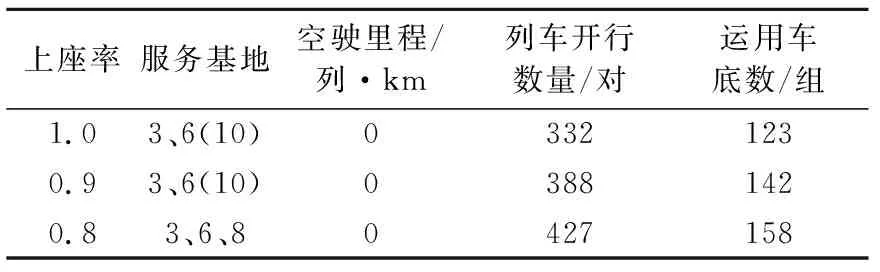
表3 动车所布局与列车开行方案关系分析Tab.3 Analysis of the relationship between the location of EMU depot and line planning

由表3可知，当列车上座率由1.0降至0.9时，动车所选址方案和空驶距离并未发生改变；当列车上座率由0.9降至0.8时，列车开行对数和运用车底数继续增加，为了避免动车组出入动车所产生空驶，需要增设一个动车所来承担相应的动车组存放与检修任务，此时非动车所直接关联车站的动车组出入动车所的空驶里程为0.综合考虑不同服务水平下的列车开行方案，在站3与站6设置动车所将有助于后续增开列车，提高服务质量.当因地理位置因素造成动车所建设成本升高，远高于因空驶距离增加造成动车组运用数量增加的成本以及动车组列车上座能力利用虚弥成本，可容许适当的列车空驶.

4 结论

针对动车所选址问题与列车开行方案编制问题协同优化，建立了混合整数规划模型，并设计拉格朗日松弛算法求解.主要研究结论如下：

1)相比于传统的列车开行方案优化模型，能有效地降低动车组出入动车所空驶成本和减少动车组运用数量，达到合理利用动车组资源的目标.

2)优化模型将动车所选址问题与线路运营组织问题联系在一起，有助于前期点线规划设计方案更好地为后续运营组织服务.

3)优化模型能够更好地揭示客流、列车方案与动车所布局之间的联动关系，其中空驶距离以及上座率是其联动关系的指标反映形式.

4)由于沿用文献[9]的区段客流数据和列车开行方案备选集设计方式，比较适用于归并后的由大站构成的路网.未来的研究中将考虑含有不同等级车站的路网，以及基于此路网生成的较为全面的列车开行模式；此外，考虑将不同规模动车所的能力阈值和建设成本应用在模型中也是进一步研究方向.