考虑时空相关性的网络交通流短期预测

邵春福，薛 松，董春娇，王晟由，庄 焱

(北京交通大学 综合交通大数据应用技术交通运输行业重点实验室，北京 100044)

随着交通现代化水平的提高，大数据、人工智能、车联网技术和智能管理技术的快速发展，使得及时、合理、可靠的获取交通流数据成为了现实.为了充分发挥现有交通硬件设施作用，诸多城市建设了大数据平台进行交通流预测，挖掘交通流数据潜在的规律性，并提取和加工交通流信息，为交通参与者提供出行服务[1].但由于交通流的随机性，准确的交通流预测较为困难，为了解决这一问题，国内外学者采用了多种技术对交通流进行建模.

深度学习作为一种新兴的智能预测模型算法，受到了国内外学者的广泛关注.基于深度学习的智能预测模型已成为一种主流趋势.Zhang等[2]提出了基于深度信念网络的交通流预测模型，并利用遗传算法来寻找不同时间段下的最佳参数；Jin等[3]提出用贪婪逐层法来改进堆叠自编码模型，实验证明改进后的模型在精度方面要优于支持向量机模型(Support Vector Machine, SVM)以及深度信念网络模型；Soua等[4]以深度信念网络模型为架构，利用DS证据理论融合数据流(流量、天气)以及事件数据来预测交通流.近年来，大量学者证明了循环神经网络(Recurrent Neural Network, RNN)在处理时间依赖性方面要优于其他模型；Madan等[5]引入离散小波变换对数据进行变换，并分别利用整合移动平均自回归(Autoregressive Integrated Moving Average, ARIMA)和RNN进行预测，实验证明了RNN在预测时间序列方面的优势；Kim等[6]以RNN模型为基本架构，结合路网数据，通过创建时空图来推断相邻路段之间的相互作用以及时间序列数据的时间动态来预测不同路网的交通速度.然而，传统的RNN虽然考虑了时间序列之间的关系，但存在梯度消失和梯度爆炸等问题.为了解决上述问题，Ma等[7]提出了一种长短时记忆神经网络(Long Short Term Memory, LSTM)的方法来获取时间序列的长时依赖性.为进一步提升模型的预测精度，温慧英等[8]引入了BLSTM，该模型通过前向计算关联历史数据，后向计算关联未来数据，此计算方式能够更好地处理时序数据中的周期性，提高预测精度.

为了发挥各种预测方法的优点，以求得到更加理想的预测效果，李明明等[9]提出了一种基于LSTM与反向传播神经网络的组合模型，通过LSTM与反向传播神经网络模型来模拟长期依赖性并确定时间序列问题的最佳时滞；Wei等[10]提出了一种自编码器长短期记忆预测模型，该模型利用自编码器获取交通流的内部关系，并用获取的特征数据和历史数据对交通流数据进行预测；罗向龙[11]等通过结合深度信念网络模型与支持向量回归分类器(Support Vector Regression, SVR)，利用深度信念网络模型学习交通流特征，并用SVR模型进行流量预测；Mihaita等[12]提出了一种卷积神经网络(Convolutional Neural Network, CNN)与LSTM相融合的时空预测模型，并将模型应用于路网交通拥堵预测，研究表明CNN-LSTM模型在预测精度上始终要优于传统预测模型，但相应地增加了模型的训练时长，在效率方面难以得到保证，未能充分发挥组合模型的优势.

受BLSTM以及时空组合模型在交通流预测中成功应用的启发，将交通流预测分为状态变量的选择以及预测模型两部分，采用PCC算法对状态变量进行选择，该算法由于实现简单、计算速度快而引起人们的广泛关注，核心思想是用协方差除以两个变量的标准差之积来表征变量间的关联程度；采用BLSTM预测所有选定站点的交通流量.PCC-BLSTM模型融合PCC算法计算路段间的空间相关性，通过设置不同的空间阈值筛选出与目标断面空间相关的上下游路段，并将筛选出的路段作为BLSTM预测模型的输入数据，最后使用网络交通流数据对模型预测性能进行验证.

1 基于时空特征交通流预测模型

1.1 空间特征挖掘

(1)

式中：rAB为A，B两路段之间的相关程度，即相关性度量；T代表时间序列长度.当rAB越接近于1，表明目标路段与相邻路段的相关程度越大；当rAB=0时，表明目标路段与相邻路段之间无相关性；当rAB<0.5时，表明目标路段与相邻路段之间相关程度较低[13].为保证预测精度，将0.5≤rAB≤1作为空间相关性的阈值范围.

1.2 时间特征挖掘

交通流数据不仅在短时间内具有较强的相关性，而且在长周期内也存在依赖性，LSTM模型难以提取数据中的周期性变化，为了解决这一问题，本文引入双向长短时记忆模型(BLSTM)来挖掘交通流的时间特征.BLSTM是LSTM的一种改进模型，它可以有效地弥补传统的神经网络无法对长时间序列有效处理的缺点[14].BLSTM采用独特的记忆模块来代替隐含节点，记忆模块可以降低特征之间的关系，从而增加模型的鲁棒性以及泛化能力，并解决神经网络中梯度消失的问题.记忆模块增设了输入门，输出门以及遗忘门，结构如图1所示.输入门可以通过sigmoid函数得出概率是否增加一些新的信息；遗忘门可以通过sigmoid函数得出概率来决定是否要抛弃一些历史信息；输出门让神经元的输出可以‘保存’，并作为输入层作用于其他时间段，即第m层神经元在t时段的输出不仅与该层t时段的输入有关,也与其余m-1层的输出有关，是历史时间关系共同作用的结果，一个记忆模块在t时段的计算公式为

图1 BLSTM结构Fig.1 BLSTM structure

中间状态

rt=τ(ht-1×Whc+Xt×Wxc+bc)

(2)

输入门

it=σ(ht-1×Whi+Xt×Wxc+

Ct-1×Wci+bi)

(3)

遗忘门

ft=σ(ht-1×Wht+Xt×Wxt+

Ct-1×Wct+bt)

(4)

输出门

ot=σ(ht-1×Who+Xt×Wxo+

Ct-1×Wco+bo)

(5)

更新状态

Ct=ft×Ct-1+rt×it

(6)

输出

ht=ot×τ(Ct)

(7)

式中：rt，it，ft，ot，Ct，ht分别代表中间状态，输入门，遗忘门，输出门，更新状态以及t时段的输出结果；W代表权重矩阵；b代表偏置向量；σ和τ分别表示sigmoid，tanh函数;Xt为t时段的输入数据.BLSTM可以从两个方向输入序列即上层是按X1到Xt正向计算一遍，得到并保存每个时段隐含层的输出，下层则是按Xt到X1反向计算一遍，得到并保存每个时刻向后隐含层的输出，最后对应时段的两次结果的平均值就是最终的输出.

1.3 时空特征矩阵重构

假设路网中有n个路段，则路网时间序列矩阵S可定义为

(8)

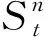
目标路段下一个时刻的交通流主要与前几个时段的实测值和空间关联路段有关.与传统的交通流短期预测模型不同，对路网时间序列矩阵S，采用PCC算法选择空间相关度高的路段，并将其重构为一个新的数据集，最终将重构后的数据集作为BLSTM模型的输入数据进行预测，所提方法具体计算过程分为8个步骤.

步骤1 构建空间相关性矩阵:根据式(1)计算两两路段之间的相关系数，并按照式(9)构建空间相关性矩阵.

(9)

步骤2 相关性排序:选定目标路段，将其余n-1个路段按照相关度，从大到小进行排列.

步骤3 重构交通量数据:筛选出相关性大于ρ的路段(ρ≤1)，并将其重构为一个新的数据集.

步骤4 交通流预测:构建BLSTM模型对重构后的数据集进行预测.

步骤5 计算模型的平均百分比误差(Mean Percentage Error, MAPE)：以MAPE最小为模型最终优化目标.

步骤6 选择不同的空间阈值ρ(ρ=ρ-0.1)，并重复步骤3至步骤5.

步骤7 确定最佳空间阈值：反复实验，根据不同空间阈值ρ所求的最小MAPE，来确定最佳空间阈值.

步骤8 预测结果以及误差分析.

时空特征短期交通流预测模型构建流程如图2所示.

图2 短期交通流预测模型流程图Fig.2 Flow chart of short-term traffic flow prediction model

2 数据计算

为了验证PCC-BLSTM模型的可行性，本文使用美国加利福尼亚州交通流PeMS系统的真测数据进行分析.该数据共包含44 681个微波传感器，以每30 s记录一次数据，记录字段包括：日期，流量，车道数，占有率以及平均速度.实验地点选取美国加州的奥克兰区域，共有28条路段，研究位置如图3所示.选定路段19-24为目标路段，由于交通流数据具有周期性，每周的数据变化情况相似，因此选取2019年9月7日至2019年9月14日的交通流时间序列作为数据样本.作为常规交通流短期预测，所有模型都采用5 min的间隔进行预测，共计288×28×7个数据.以前6 d的数据作为训练集，最后一天的数据作为测试集.

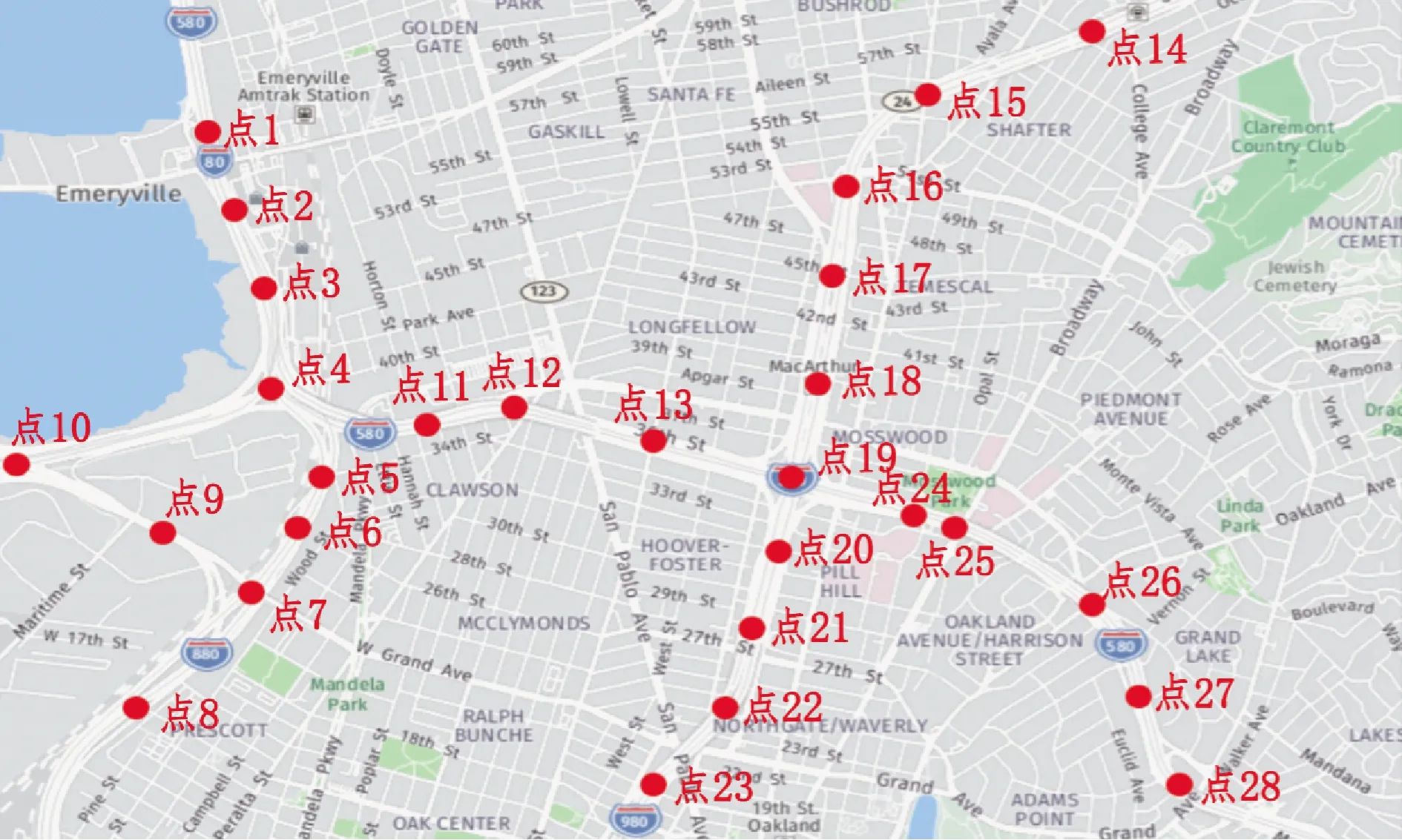
图3 实验路网Fig.3 Road network for verification

为了对模型的预测结果进行定量分析，将均方根误差(Root Mean Square Error, RMSE)、MAPE以及平稳R方(R2)作为预测评价指标，指标具体定义分别为

(10)

(11)

(12)

3 结果分析

经过多次实验，确定模型训练步数为100，隐藏神经元12个.按照第1.3节提出的流程对路段19-24的交通流进行预测，其中空间状态变量以及时间状态变量是模型的两个输入参数.空间状态变量是相关路段所形成的空间矩阵，时间状态变量是指空间矩阵所考虑的时间步长.

为研究时空状态变量对预测精度的影响，将空间阈值设为0.5，0.6，0.7，0.8，0.9，1；时间步长设定为3，4，5，6，7.不同阈值下模型的预测性能评价如表1所示.为了提高预测精度，采用PCC算法进行空间特征变量的选择.从图3中各路段的位置可知，与目标路段相关性较大的路段均位于目标路段的上下游位置，说明上下游位置的交通流量对目标路段的影响较大，符合实际情况，验证了PCC算法应用于空间特征变量选择的有效性.进一步分析时间步长对预测精度的影响，可以看出，选用不同的参数组合会改变模型预测精度，在一定范围内，预测精度随着时间步长的增大而增大.预测所使用的时间步长过长，则会加入无关的时间信息，干扰预测结果；而时间信息过少，容易导致模型过拟合.

表1 不同阈值下预测性能评价Tab.1 Prediction performance evaluation under different thresholds

表1只是列出了不同时空参数下的预测结果，图4总结了不同空间阈值下的均方误差.可以看出，在一定范围内，随着阈值的减少，路段之间的空间相关性降低.高阈值情况下，相关路段的信息过少导致预测效果不佳；低阈值情况下，加入过多无关路段信息干扰预测效果.当空间阈值ρ为0.8时，RMSE达到最小值，路段19-24在9月14日的预测值和真实值如图5所示，图中预测值的浮动范围不大，预测结果与实际值可以良好的吻合，表明PCC-BLSTM模型在实际交通场景中具有可行性.

图4 不同阈值下的误差对比Fig.4 Errors under different thresholds

图5 路段19-24预测结果Fig.5 Prediction results of road sections 19-24

为了进一步研究时空模型的预测性能，分别使用ARIMA、SVM、LSTM以及CNN-LSTM模型对路段19-24的交通流进行预测.经过多次实验，将ARIMA模型的自回归项数以及滑动平均项数分别设为3和7，差分项为2；SVM模型的核函数选用径向基核函数，惩罚因子设为0.8，迭代次数设为500；LSTM模型的隐藏神经元共有12个，时间步长设为4，迭代次数设为100；对于CNN-LSTM模型，将卷积核的大小设为3×3，卷积步长为1，CNN模型的激活函数选用Relu，优化方法选择Adam，整个模型的迭代次数以及学习率分为设为500和0.002，不同模型的流量预测结果如图6所示.可以看出，机器学习模型SVM在短期内可以很好地拟合曲线，但随着预测时间的增加，SVM模型的输出结果将会出现震荡，长时间的预测将会出现较大的误差；而线性模型ARIMA只是用一条光滑的曲线来拟合原数据，无法应对流量随机变化，预测效果最差.由于深度学习模型LSTM以及时空预测模型CNN-LSTM均属于深度学习架构，预测精度都可以达90%以上，从图中难以体现PCC-BLSTM的优势.表2总结了不同模型的性能评价结果, 根据MAPE指标，考虑了时空因素的BLSTM模型预测准确率高达94.05%，比线性模型ARIMA、机器学习模型SVM以及LSTM模型分别改善了9.05%、6.54%和3.54%，预测准确率平均可提高4.83%，可见组合模型较单一模型能展现出更好的预测效果.与同属于时空组合模型的CNN-LSTM模型相比，PCC-BLSTM在准确度上并无显著优势，但从效率角度看，该模型预测所需时间与LSTM模型相差不大，却远小于CNN-LSTM模型，并且预测精度可以得到保证.R2通常用于描述数据对模型的拟合程度，越接近1，拟合度越好，表现为拟合后的曲线与原始数据点偏差较小，一般情况下经验值是0.7，可见所有模型的预测结果均是有效的.综上所述，PCC-BLSTM充分结合了统计方法以及深度学习的优势，不仅训练效率高，而且具有良好的预测性能，能够为出行者在选择出行方式、出行路线等方面提供可靠的参考.

图6 不同模型的流量预测结果Fig.6 Flow prediction results of different models

表2 不同模型的性能评价结果

4 结论

1) PCC算法实现简单且计算速度快，考虑了不同时间下时间序列的相关性程度，适用于随机变量间的相关性判断，核心思想是用协方差除以两个变量的标准差之积来表征变量间的关联程度.BLSTM模型类似于LSTM模型，采用独特的记忆模块来代替隐含节点，从而产生对过去状态的记忆，并增加模型的鲁棒性以及泛化能力，可以有效弥补传统的神经网络无法对长时间序列有效处理的缺点，能更好地提取数据中的周期性变化.

2) 考虑到时间步长对预测精度的影响，在一定范围内，预测精度随着时间步长的增大而增大.预测所使用的时间步长过长，则会加入无关的时间信息，干扰预测结果；而时间信息过少，容易导致模型过拟合.而空间阈值过高或过低也会影响最终的预测效果.高阈值情况下，相关路段的信息过少导致预测效果不佳；低阈值情况下，加入过多无关路段信息干扰预测效果.合理设置时空阈值将提高预测精度.

3) 机器学习算法SVM适用于交通流短期预测，但随着预测时间的增加，SVM模型的输出结果将会出现震荡；线性模型ARIMA无法识别数据中随机性以及非线性，难以对流量的随机变化做出准确预测；而LSTM模型的预测结果拥有较高的预测精度，但该模型并未考虑数据中的空间信息，因此预测精度低于PCC-BLSTM模型；时空预测模型CNN-LSTM在预测精度方面与PCC-BLSTM模型无显著差异，但训练模型所耗费的时间过长，难以对路网流量实时预测.

4) PCC-BLSTM模型可以为国内交通流预测的研究和应用提供一种新思路.在后续研究中，将综合考虑速度等因素优化组合预测模型来进一步提高预测性能.此外，可尝试挖掘国内城市道路网交通流数据的时空相关性，从而进一步证明PCC-BLSTM的优越性与适用性.