基于代理模型的加工中心滑鞍有限元模型修正

陆原超，周俊荣，王瑞超，李会军

（五邑大学 智能制造学部，广东 江门 529020）

0 引言

伴随着机械制造加工业的飞速发展，对加工中心的加工精度和加工效率等要求不断上升，对加工中心的设计需求提出了新的挑战，传统的经验设计方法已经不能满足新的设计需求，有限元分析越来越多地应用到加工中心的设计过程之中[1]。有限元分析的第一步，就是建立一个准确的有限元模型，但由于加工中心结构的复杂性[2]，模型修正技术应运而生[3]。有限元计算结构输出与输入为隐函数关系[4]，修正过程中频繁调用有限元模型，需要大量的计算量，通过代理模型将有限元模型用显函数近似可以大幅减少计算量，提高模型修正效率[5]。常用的代理模型有多项式响应面[6]、支持向量回归[7]和Kriging模型[8]等。

1 理论基础

1.1 模型修正理论

有限元模型修正起源于20世纪60年代，可以分为矩阵法和参数法。矩阵法通过修改结构刚度矩阵与质量矩阵等减小与真实结构间的误差，但由于矩阵法缺少物理意义且不具备工程意义，已经逐渐被淘汰。参数法通过修改密度、弹性模量、连接刚度等物理参数，保证了修正过程的物理意义，逐渐成为研究重点[2]。

通过修正有限元模型的设计参数，参数型模型修正方法逐步减小响应计算值与实测值之间的误差，将模型修正这一参数辨识问题转变为优化问题，可将优化目标函数F(x)写为

其中：x是待修正参数的向量；ri是第i个响应的残差函数；

ωi是第i个残差函数的权重系数。

1.2 Kriging模型

传统参数型模型修正方法需要不断地调用有限元模型参与计算，由于有限元模型计算的黑箱特性，通过建立一个可以模拟输入与输出之间函数关系的显式代理模型可以大幅减少计算量，Kriging模型就是一种常用的代理模型[4，6]。Kriging模型可以分为回归部分与随机响应部分，写为：

其中：y(x)是Kriging模型的响应预估值；f(x)是Kriging模型的回归部分，是关于x的多项式函数，用来拟合整体趋势；Z(x)是Kriging模型的随机响应部分，用来拟合局部变化。Kriging模型不仅能得到预估值，还能得到方差，并利用方差在设计空间中重新取样，对自身进行更新从而获得较高的模型预测精度。重新取样依据的规则被称为加点准则，最大期望改善（Expected Improvement，EI）准则是使用较为广泛的加点准则，其将EI函数定为评价指标来表征改善程度I(x)，并将EI函数最大值的设计点作为新设计点添加到设计点集中更新Kriging模型，如此循环直至满足收敛准则。改善程度I(x)可以写为

其中：Φ是标准正态累计分布函数；ψ是标准正态分布概率密度函数。通过不断迭代添加新设计点更新Kriging模型，可以使得模型自适应进化，从而满足工程需要。

2 滑鞍模态试验

滑鞍是加工中心主要移动部件，直接与电主轴相连，提供加工中心Z轴移动。为了获得滑鞍的模态参数，对其进行了力锤敲击模态试验。实验过程中选用了东方所INV9832-50三向加速度传感器与奇石乐9722A2000力锤，在滑鞍表面均布测点，共布置了20个测点。测试过程采用移动传感器法，保持力锤在同一敲击点不变，移动传感器遍历所有测点，数据采集依靠基钛克Impaq频谱分析仪，采样频率为5000 Hz，最终结果导入到计算机中，运用专业软件ME’SCOPE进行模态分析，得到滑板模态参数，如表1所示。

表1 滑鞍模态试验实测值

3 构建Kriging代理模型

3.1 有限元模型建立

滑鞍整体尺寸约为320 mm×220 mm×110 mm，根据滑鞍几何尺寸在SoildWorks中建立起三维模型，将三维模型导入到Hypermesh 中划分结构化网格，网格模型如图1所示。

图1 滑鞍有限元网格模型

滑鞍依靠导轨滑块和螺母丝杆与滑板相连，用弹簧阻尼单元对滑鞍边界条件进行模拟，用弹簧的刚度值代替接合面刚度值，其中导轨滑块可以简化为法向弹簧与轴向弹簧，丝杠螺母可以简化为径向弹簧和轴向弹簧，其接触刚度值可以通过厂家手册查得，滑块的法向刚度k1为8.62×108N/m，切向刚度k2为5.64×108N/m；丝杆的径向刚度k3为6.32×108N/m，轴向刚度k4为7.32×108N/m。滑鞍材料为灰铸铁，材料参数取自ANSYS材料库，弹性模量E为110 GPa，密度ρ为7200 kg/m3，泊松比μ为0.28。边界条件设定模拟模态试验时的外部条件，将有限元模型导入到ANSYS Workbench中进行有限元模态分析，与模态试验的结果进行对比，如表2所示。

表2 滑鞍固有频率实测值与计算值的对比

从对比结果可以看出，计算固有频率和实测固有频率最大相对误差为19.37%，发生在第六阶，前六阶的平均误差为11%左右，表明有限元模型虽然能一定程度上模拟真实模型，但仍需要进一步修正以满足工程需求。

3.2 参数选择与灵敏度分析

由于滑鞍材料参数选用的是ANSYS材料库中灰铸铁的材料参数，与滑鞍实际材料可能有所偏差，故将滑鞍材料参数纳入修正参数的选择当中。导轨滑块和丝杆螺母的刚度参数是从厂家手册上查得，但在有限元模型中将其简化为弹簧阻尼单元，因此将弹簧刚度也纳入修正参数当中。综上所述，初步选择了滑鞍密度参数ρ、滑鞍弹性模量E、滑鞍泊松比μ、法向弹簧刚度k1、切向弹簧刚度k2、径向弹簧刚度k3和轴向弹簧刚度k4等7个结构参数作为设计参数。

对上述7个待修正参数进行模态频率灵敏度计算，计算结果如图2所示。可以看出滑鞍密度ρ、弹性模量E、法向弹簧刚度k1、径向弹簧刚度k3和轴向弹簧刚度k4对滑鞍模态频率的灵敏度较高，因此，有限元模型修正的修正参数选 择 ρ、E、k1、k3和k4等5 个设计参数。结合现实考虑，修正参数的取值范围在其初值的0.8～1.2倍之间。

图2 设计参数灵敏度分析

3.3 自适应Kriging模型构建

实验设计是一种基于数理统计和概率论的科学方法，可以通过较少的试验次数得到输入与输出间的关系。拉丁超立方实验设计是蒙特卡罗方法的一种，具有较高的采样效率，在实际应用中使用较广。五设计参数的拉丁超立方实验设计，取样方式选为中心复合设计，初始设计点共有27个。将选定的参数提交到有限元模型中参与计算，得到对应的前六阶固有频率数值，根据此输入与输出关系可以构建出初始的Kriging模型，然后可以根据EI加点准则增加细化点，以0.01为收敛值，最终新增了4个细化点，构建成立自适应Kriging模型。以法向弹簧刚度k1和径向弹簧刚度k3与第一阶固有频率f1的关系为例，标准和自适应Kriging响应面模型如图3所示。

从图3可以看出，自适应Kriging模型在函数的极大值点附近插入了新设计点，从单点极大值变成了两点极大值。从拟合优度来看，标准Kriging模型的拟合优度为96.52%，自适应Kriging 模型的拟合优度为99.24%，相较于标准Kriging 模型拟合精度得到了提高，是对有限元模型更高精度的近似。

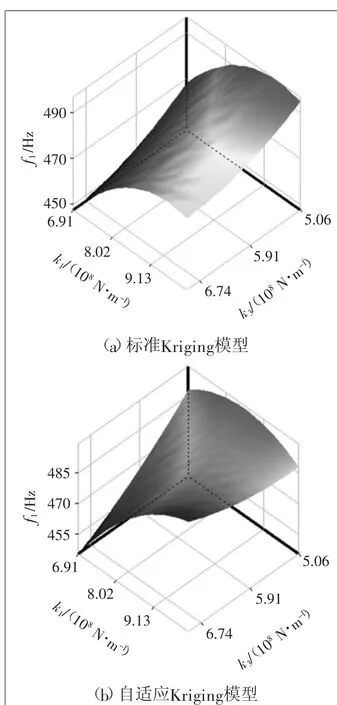
图3 标准Kriging和自适应Kriging一阶固有频率响应面

4 模型修正

基于自适应Kriging模型，采用遗传算法搜寻设计空间内目标函数的最小值，遗传算法初代种群大小设定为1000，子代种群大小设定为500，最大迭代代数为20，允许的最大帕累托百分比设定为70%，稳定收敛阈设定为2%，修正前后各参数与结果的对比列在表3。从中可以看出，变动量较大的为滑鞍的弹性模量、滑块法向接触刚度与丝杆轴向接触刚度，但均未接近设计空间边缘，有较高的置信度。

表3 修正参数在模型修正前后的对比

表4给出了修正之后的有限元模型前六阶模态计算频率与实测频率的对比结果。从中可以看出，与未修正的有限元模型相比，修正后的模型与实际模型的相似度更高，最大相对误差从原先的19.37%降低为4.52%，最大相对误差在5%以内，可以满足工程计算需求。

表4 模型修正后计算频率与实测频率的对比

5 结语

基于自适应Kriging模型，本文对有限元模型进行了参数修正，较好地平衡了计算效率与计算精度，最终修正后的有限元模型与实测模型相对误差降至5%以下，可以满足工程计算需求。