交直流混合配电网VSC与分布式电源三层协调规划方法研究
2021-09-25崔艳妍
韦 涛,苏 剑,崔艳妍,王 罡
(1.中国电力科学研究院有限公司,北京 100092;2.国网河北省电力有限公司,河北 石家庄 050031)
0 引言
风力、光伏等分布式电源(Distributed Generation,DG)以其清洁、可再生的特点受到广泛关注,基于可再生能源的DG大规模接入配电网已经成为必然趋势[1]。目前,交流电网受限于传输能力,对可再生能源的消纳能力趋于极限。随着电力电子元件的发展,直流配电技术日益成熟,直流配电网相比交流配电网具备更强的供电能力[2],[3]。现阶段对原有线路进行部分直流改造,形成交直流混合配电网是最为合理的方案[4]。
目前,针对交直流混合配电网优化规划的相关研究主要集中在纯直流配电网或直流微电网等特殊场景。文献[5]建立了含电动汽车充放电站的直流配电网规划模型,采用混合编码方法,利用自适应遗传算法求解,最终得到规划方案。文献[6]考虑典型DG和负荷的时序特性建立直流配电网经济性最优模型,利用自适应遗传算法交替求解,验证了直流配电网优势更为明显。文献[7]基于二阶锥规划提出了一种考虑网络动态重构的DG选址定容优化方法。文献[8]考虑DG接入对配电网运行电压和网损的影响,建立了基于电压灵敏度的交流DG规划模型,得到了DG容量接入方案。文献[9]基于源荷互动响应模式提出了一种计及电源-用户互动的DG双层规划方法,分别以经济性、环保性、电压质量和安全性综合最优以及年运行成本最优为模型目标决策的DG的选址定容方案。
由上述文献可以发现,传统的DG规划都是在交流配电网中进行,DG规划与交直流配电网改造独立研究没有充分考虑二者之间的耦合关系,难以获得最优的规划方案和经济效益。
本文从考虑全社会综合效益最优出发,研究了配电网直流改造与DG的联合规划方法。首先,对交直流混合配电网中各元件进行建模;其次,建立了交直流混合配电网电压源换流器(Voltage Source Converter,VSC)与DG三层协调规划模型,采用精英保留遗传算法以及二阶锥规划算法对模型进行求解;最后,采用IEEE 33节点系统对所提出的方法进行了验证。
1 互联系统线性变参数模型
VSC是一种将交流电转化为直流电的换流装置,综合考虑其经济性、安全性等问题,在中压层面,本文采用单极对称结构的VSC进行改造。改造过程中,直流线路中有一个VSC处于Vdc-Q控制模式,实现对直流电压的稳定控制。VSC运行损耗计算式如下:


图1所示为传统中压配电网,电压等级为10 kV。图2所示为交直流混合中压配电网,由于线路1中所带的直流电源和负荷较多,因此,选择将其改造为直流线路,VSC配置在直流线路首端,用来将下游线路转换为直流线路,该VSC采用Vdc-Q控制方式建立直流线路的电压。
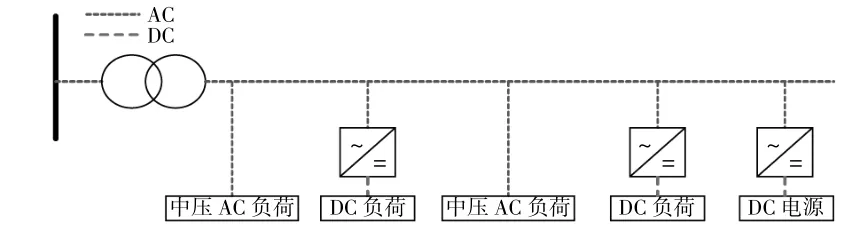
图1 传统中压配电网Fig.1 Traditional medium voltage distribution network

图2 交直流混合中压配电网Fig.2 Hybrid AC/DC medium voltage distribution network
2 协调规划模型
本文所建立的协调规划模型分为三层,上层以整体改造工程社会效益最大为目标,中层以安装DG社会效益最大为目标,下层以网络运行总效益最大为目标。优化变量分别为VSC位置容量、DG位置容量以及各DG注入网络的有功功率。
2.1 上层规划目标函数及其约束条件
2.1.1 目标函数
上层规划以整体改造方案总收益最大为目标函数,已知量为VSC的单位容量投资年费用与运行维护年费用,优化VSC的位置与容量。目标函数如下:

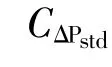
其中:
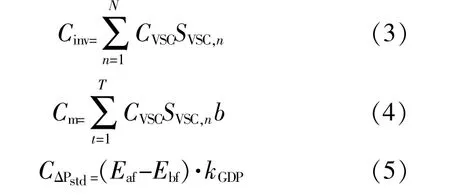
式中:N为VSC安装个数;CVSC为VSC的单位容量投资成本;SVSC,n为第n个VSC的安装容量;T为年数;b为VSC的维 护费 用系 数;Ebf,Eaf分别 为改造前、后规划年限内总用电量;kGDP为用电量与GDP的相关系数。
2.1.2 约束条件
换流站VSC的容量受限于物理因素等原因,必须小于其最大可建设容量,于此同时,VSC在直流线路中充当电源,直流线路中负荷总量不能超过VSC容量。
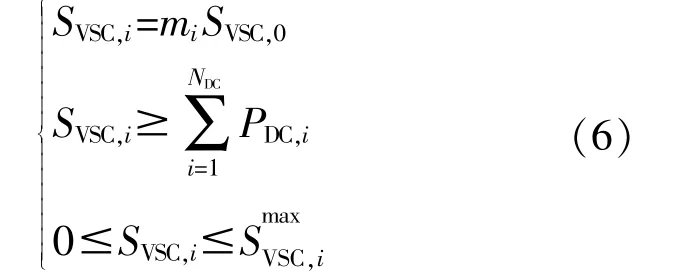
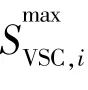
2.2 中层规划目标函数及其约束条件
2.2.1 目标函数
中层规划以分布式电源安装方案总收益最大为目标函数,已知量包括典型日各类电源投资年费用与运行维护年费用,优化DG的位置与容量。目标函数如下:

式中:Zdown为下层目标函数,即网络优化运行目标。
由于DG直流接入相比交流接入可以省去一部分逆变器费用,因此DG的投资费用须要考虑直流改造的相关影响。在中层模型中,DG投资费用分为两部分:直流线路接入投资费用和交流线路接入投资费用,Cinv,Cm的表达式分别为
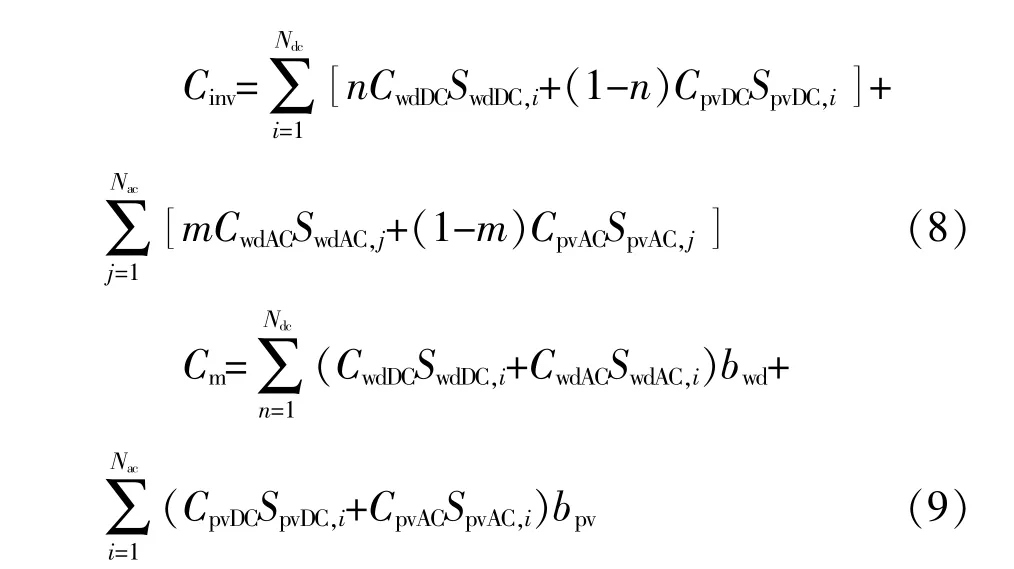
式中:Ndc为DC线路DG安装个数;CwdDC为直流线路风电机组DG的单位容量投资成本;SwdDC,i为直流线路位置i风电机组DG的安装容量;CpvDC为直流线路光伏电池DG的单位容量投资成本;SpvDC,i为直流线路位置i光伏机组DG的安装容量;n表示直流线路位置i安装风电机组或光伏机组,取值分别为1或0;Nac为交流线路DG安装个数;CwdAC为交流线路风电机组DG的单位容量投资成本;SwdAC,j为交流线路位置j风电机组DG的安装容量;CpvAC为交流线路光伏电池DG的单位容量投资成本;SpvAC,j为交流线路位置j光伏发电DG的安装容量;m表示交流线路位置i安装风电机组或光伏电池,取值分别为1或0;bwd为风电机组DG的维护费用系数;bpv为光伏机组DG的维护费用系数。
2.2.2 约束条件
DG的建造容量应小于其最大可建设容量,并且地区安装DG大多以总容量为目标,因此约束条件中要求总安装容量为定值。

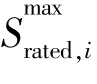
2.3 下层规划目标函数及其约束条件
2.3.1 目标函数
下层模型从全社会角度以整体系统改造年限内运行效益最大化为目标函数,已知量包括典型日每个时段负荷大小、风力发电出力和光伏发电出力;下层优化变量为光伏、风机两类DG的有功出力以及无功出力,取值上限为最大出力能力。
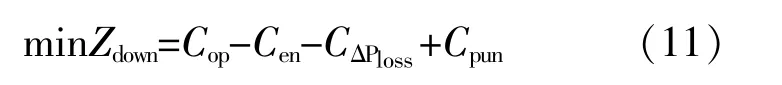

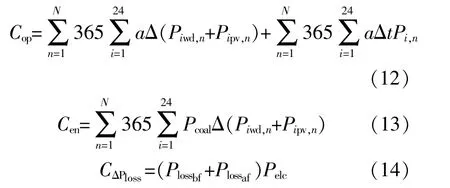
2.3.2 约束条件
下层模型考虑网络的具体运行情况,优化DG每个时刻的出力以及充分发挥DG的能力,其大小应满足DG最大可利用功率约束、消纳率约束和混合网络的潮流约束。

对网络进行直流改造并接入DG会同时影响网络的整体潮流,进而影响网络的节点电压与网络损耗,二者的规划结果必须同时满足交流电网侧与直流电网侧的潮流方程,并且负荷侧电压及功率不能越限[11]。该部分潮流约束与式(2)~(15)构成VSC与DG协调优化配置的三层规划模型,每层模型的决策变量以及模型之间的交互关系如图3所示。
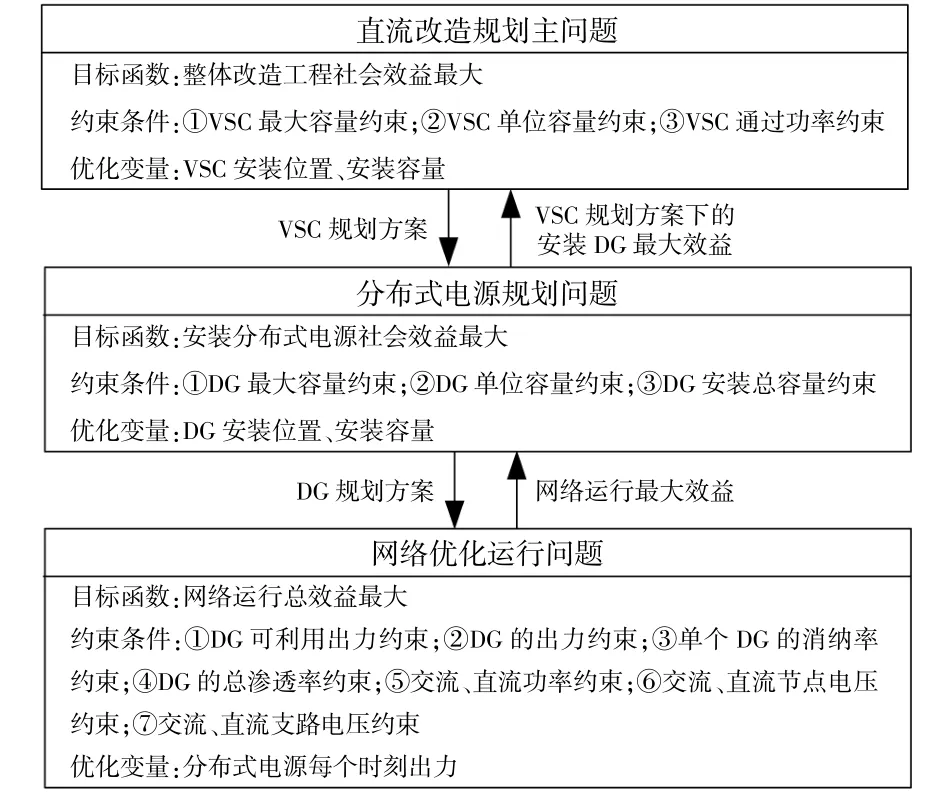
图3 规划模型的交互关系Fig.3 Interaction diagram of the planning model
3 模型解法
由于直流线路改造问题主要针对直流负荷以及DG接入,其候选位置较少,因此本文采用候选位置选取法求解上层模型,上层模型确定VSC的候选位置及容量后,为中层模型提供网架信息。中层模型采用精英保留策略遗传算法[12]求解,对DG候选位置及容量进行编码,在遗传操作中,本文采用具有保留策略、自适应交叉率、变异率和最优个体最少保留代数与最大遗传代数相结合的终止进化准则的改进遗传算法,设置迭代次数使其达到收敛,从而获得全局最优解。中层模型确定网架中的DG位置及容量,为下层模型提供运行状态具体信息,将自身结果返回上层模型。下层模型通过对约束条件进行锥旋转变化,在Matlab-YALMIP平台下利用CPLEX算法包进行求解,基于上层及中层模型网络信息,优化得到网络的最佳运行状态,并将其返回中层模型。
3.1 上层模型解法
由于现有负荷大多为交流负荷,并且直流配电成本昂贵,因此不适宜将现有交流配电网全部改造为直流。将现有交流配电网的部分线路改造为直流是目前较为合理的方式,而VSC的选址定容问题可视作直流改造线路的选取问题。本文建立了基于节点数量、直流负荷占比、功率限制的直流线路选取原则,具体包括改造线路节点数选取原则、线路直流负荷占比选取原则和改造线路VSC容量选取原则。
改造线路节点数选取原则:
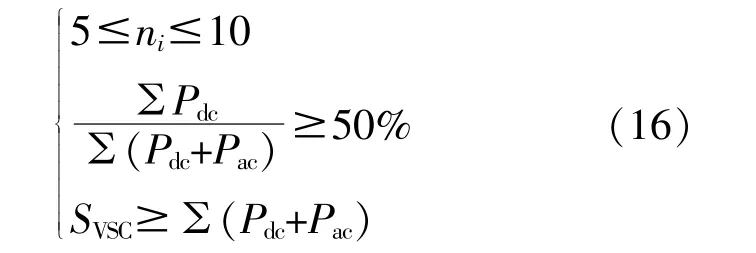
式中:ni为线路中节点个数;Pdc,Pac分别为线路中直流、交流负荷的全年平均功率;SVSC为线路VSC的容量。
根据上述备选位置选取依据,在网络中确定VSC候选位置及容量。
3.2 中层模型解法
中层模型采用精英保留遗传算法进行求解,对给定候选位置的DG安装位置和容量进行编码,如图4所示。图中Sk为在候选位置k安装DG的容量,当Sk为0时,表示在该候选位置不安装DG。

图4 DG编码图Fig.4 Code pattern of the DG
3.3 下层模型解法
下层模型中存在多个二次项方程,因此可将本文问题转为二阶锥优化问题,具体锥模型转化方式参见文献[13]。通过变换,下层规划问题可以采用CPLEX算法包进行求解。
4 算例分析
本文以IEEE 33节点配电系统为例,研究交直流混合配电网考虑VSC与DG的选址定容模型。如图5所示,算例中负荷水平为2 810 kW,其中,负 荷 点3~8,14~17,29~32为 第 一 类 负 荷,负荷 点1~2,18~21,25~28为 第 二 类 负 荷,负 荷 点9~13,22~24为 第 三 类 负 荷。
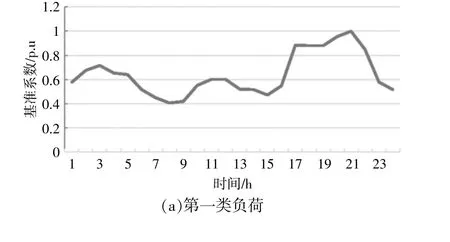
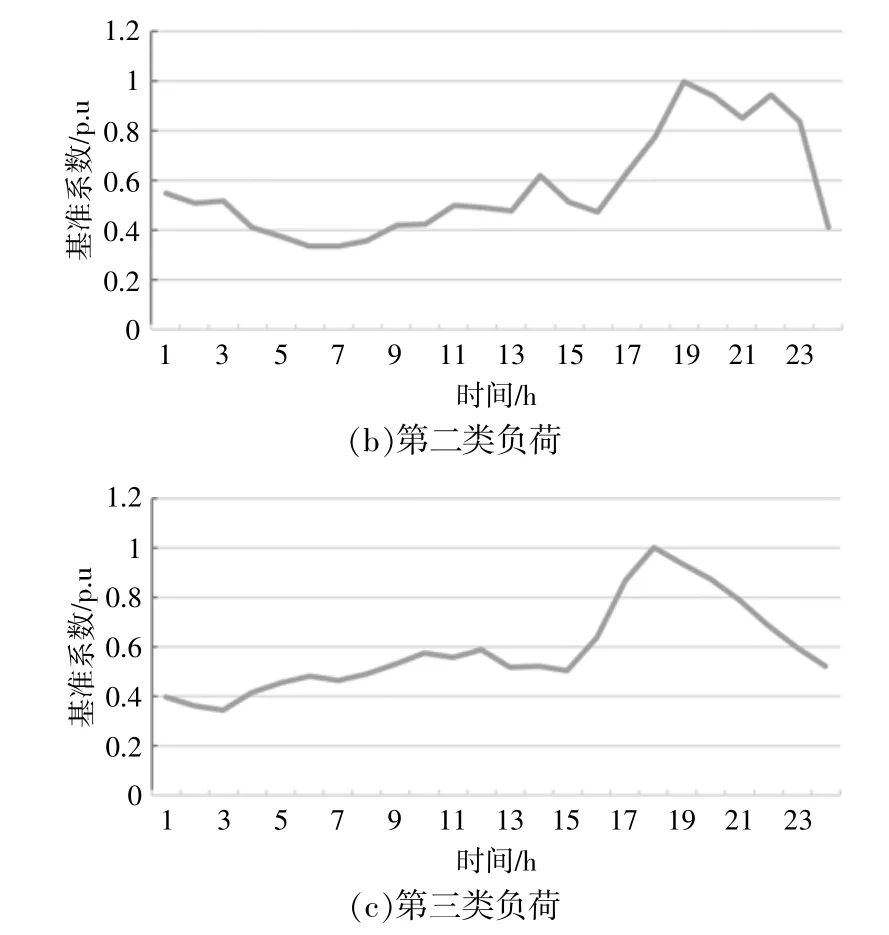
图5 3类负荷典型日曲线Fig.5 Three typical curves of loads
假设规划目的为满足5 a内10%的负荷增长率,根据VSC位置选取原则,待选VSC安装节点为10和25,待选光伏电源安装节点为4,21,23,30,各节点最大安装容量设为300 kW。
风力发电机、光伏发电机维护费用系数取0.1,单位电量运行费用系数取0.01;购电电价取0.5元/(kW·h);现 阶 段 在 规 划 年 限 内 网 络 损 耗 费用为445.33万元。单位电量碳税费用为0.18元/(kW·h)。DG单位容量设备投资年费用见表1。

表1 DG单位容量设备年投资费用Table 1 Annual investment of DG unit cost 元/kW
根据上层模型解法确立VSC的候选位置,直流改造共分为3种方案,如图6所示,10节点安装VSC、25节点安装VSC以及10,25节点共同安装VSC。遗传算法种群数量设定为100,交叉概率为0.9,变异概率为0.1,最大迭代次数为500代。
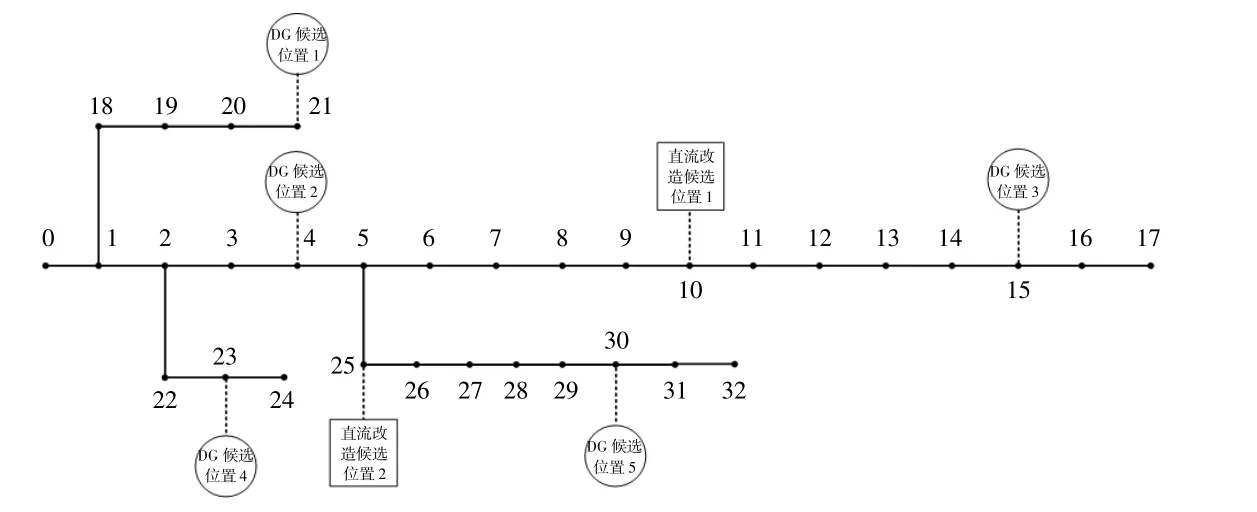
图6 IEEE 33节点算例拓扑图Fig.6 IEEE 33 node distribution network topology
算例分析共分为两部分,第一部分为经济效益分析,第二部分为系统运行分析。
4.1 经济效益分析
经过本文方法规划后得到的新网络拓扑如图7所示。具体规划方案如表2所示。根据算例结果可知,各节点的DG均达到约束中的最大可安装容量,通过在线路中安装DG,可以缓解线路的重载情况。

表2 规划装置类型及容量Table 2 Location and capacity of devices

图7 IEEE 33节点算例规划后拓扑图Fig.7 IEEE 33 node distribution network topology after planning
本文设置3类场景,其中,场景1为联合规划直流与DG,场景2仅规划DG,场景3仅规划直流改造,对其经济效益进行分析,结果见表3。

表3 不同场景经济效益分析Table 3 Economic benefit analysis of different scenes万元
由表3可以看出:场景1与场景2的DG运维费用相同,但场景2的投资更少,其原因为DG接入直流线路投资少;经过场景1改造,整体网络的损耗得到了明显改善,从原有的445.33万元降低为232.22万元,总体收益为213.11万元,降损达到48%,而场景2与场景3降损仅为18%和33%。由此可见,场景1可以大幅降低网络损耗费用。尽管场景1的VSC投资费用较高,但其对于线路的重载情况改善可以起到非常大的作用,所带来的GDP收益相比投资更为巨大,达到54 113.79万元,为场景2的3.45倍,场景3的1.15倍。
4.2 系统运行分析
在典型日曲线基础上,针对光伏出力波动较大的12:00和负荷波动较大的23:00两个时刻,本文对3类场景下的规划结果应对功率波动时的系统运行状态进行了分析。12:00时刻,不同场景5 a内各节点电压情况如图8所示,电压越限情况如表4所示。
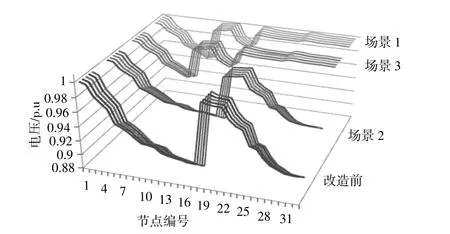
图8 不同场景5 a内12:00时刻各节点电压情况Fig.8 Voltage of each node at 12 points in different scenarios
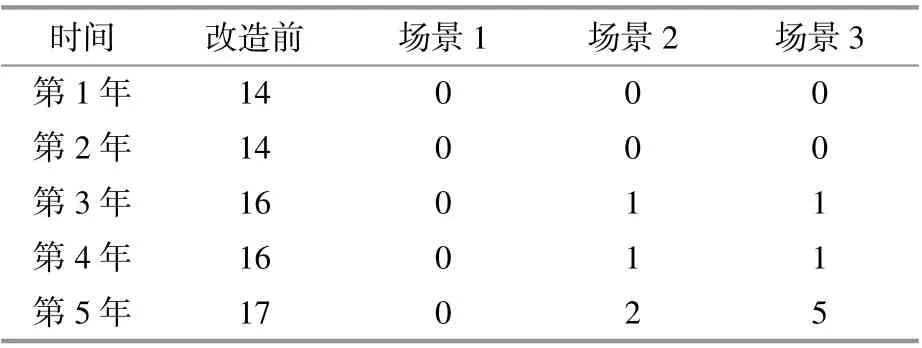
表4 不同场景12:00时刻电压越限节点个数Table 4 The number of voltage crossing nodes at 12 points in different scenarios
由图8可以看出:改造前网络节点越限个数超过整体网络的50%,通过场景1可以实现网络电压始终处于正常状态,效果最好;场景2和场景3对网络电压起到缓解作用,但其在负荷逐年增长时仍会出现节点电压越限的情况。
典型日23:00时刻不同场景5 a内各节点电压情况如图9所示,电压越限情况如表5所示。

图9 不同场景23:00时刻各节点电压情况Fig.9 Voltage of each node at 23 points in different scenarios
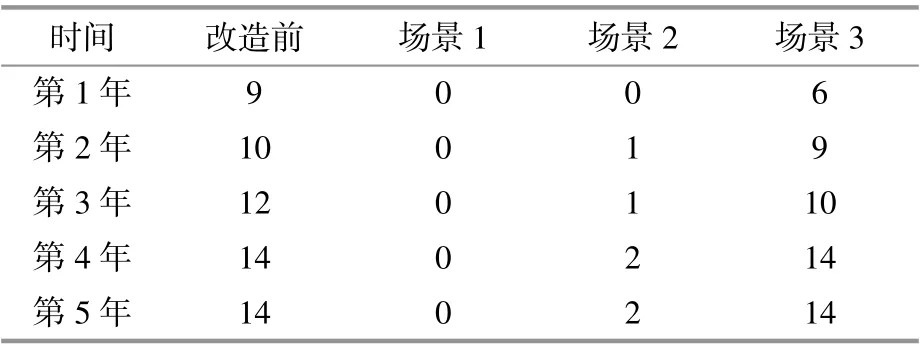
表5 不同场景23:00时刻电压越限节点个数Table 5 The number of voltage crossing nodes at 23 points in different scenarios
可见,相比12:00,23:00时刻安装DG对于缓解网络的电压质量较弱,其主要原因为DG中的光伏在夜间无法工作,对夜间负荷的电能质量缓解情况较弱。直流改造可以有效缓解这一问题,但通过直流改造仍然无法避免某些节点电压越限。同时规划直流与DG可以实现节点电压全部正常,从而使网络处于高效稳定运行状态。
4.3 算法的收敛性分析
本文上层优化模型根据直流改造节点选取原则确定直流改造方案;中层优化模型采用精英保留策略遗传算法求解,同时根据最优个体最少保留代数与最大遗传代数相结合的终止进化准则制定收敛条件,其中,精英保留策略可以避免算法陷入局部最优,终止进化准则可以保证算法的收敛效果;下层模型优化DG每个时刻的出力,其本质是一个最优潮流问题,本文将下层模型转换为二阶锥规划模型并调用CPLEX算法包求解,且收敛性已经在文献[13]中证明。
本文设置的收敛条件为连续3次迭代结果误差小于0.1%时跳出循环,认为收敛。由于采用遗传算法进行求解,每次计算迭代收敛情况不一样,本文选取5次结果的平均值,统计收敛情况如图10所示,可以看出,采用本文算法在迭代45次左右达到收敛。
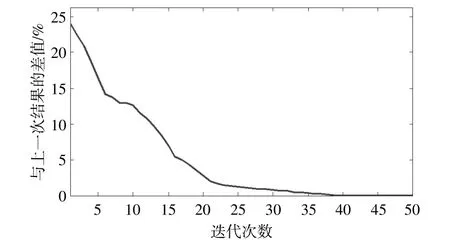
图10 算法的收敛情况Fig.10 Algorithm convergence diagram
5 结论
本文从全社会效益最大化角度,充分考虑了VSC与基于可再生能源的DG在投资费用以及运行层面的相互耦合影响关系,建立了交直流混合配电网VSC和DG三层优化规划模型,并针对各层模型的特点提出不同的算法对其进行求解。算例结果表明:VSC和DG联合规划方法相对单独规划VSC或DG,能够减少投资费用,提高运行效益,有利推动全社会GDP效益增长;同时能够有效缓解运行中线路重载的问题,改善系统电压质量,提高配电网运行的安全性。
