基于LMD-IMVO-LSSVM的短期风速预测
2021-09-25桑茂景谢丽蓉李进卫
桑茂景,谢丽蓉,李进卫,王 斌,3,杨 欢,4
(1.新疆大学 电力系统及发电设备控制和仿真国家重点实验室风光储分室,新疆 乌鲁木齐 830047;2.中船重工海为(新疆)新能源有限公司,新疆 乌鲁木齐 830002;3.山东钢铁集团日照有限公司,山东 日照276805;4.清华大学 电力系统及发电设备控制和仿真国家重点实验室,北京 100084)
0 引言
随着化石燃料的大量使用,化石能源枯竭及其所带来的环境问题日益严峻。清洁、可持续的风能逐渐受到各国的高度重视。然而风能的间歇性、随机性和不可控性,使得风电大规模并网存在巨大的挑战,因此准确有效地预测风速对电力系统的平稳运行意义重大。
近年来,科研人员对风速预测已经做了大量的研究。目前,用于风速预测的方法主要有回归分析方法、时间序列方法、马尔科夫链方法、支持向量机方法和神经网络方法等[1]~[5]。然而,在现实风速预测中,通过以上单一预测方法往往无法达到理想的预测效果,要对单一预测模型进行一定的优化和改进来提高风速的预测精度。文献[6]采用了广义回归神经网络的预测方法对风速进行预测,该方法具有结构简单,方便实现,对训练数据数量要求不高的特点,和BP神经网络相比较,其预测的精确度和准确度有所提高;然后又对广义回归神经网络中的光滑参数进行粒子群(PSO)优化选取,使其取值不再盲目,进一步提高了其预测精度。文献[7]从4个方面对局部均值分解(LMD)和经验模态分解(EMD)进行比较,结果表明,与EMD相比,LMD可以有效地消除模态混叠,从而获得更准确的瞬时频率。文献[8]采用多元宇宙优化算法(MVO)对最小二乘支持向量机(LSSVM)模型的若干参数进行优化,取得了较高的建模精度。文献[9]利用集合经验模态分解法将风速序列分解为频率不同的若干个分量,降低了风速序列的非平稳性;然后利用花朵授粉算法优化BP神经网络构建预测模型,预测各个分量的变化趋势;最后将各个分量的预测值进行叠加组合,得出最终的风速预测值。但是上述方法均未达到理想的预测效果。
鉴于LSSVM具有较强的泛化能力以及样本问题处理能力等优点,本文采用改进多元宇宙算法(IMVO)对LSSVM参数进行寻优,并结合LMD方法,提出一种基于LMD-IMVO-LSSVM的风速预测模型。通过实验仿真分析,所提方法有效提高了风速预测的精度。
1 局部均值分解
LMD是一种新的自适应非平稳信号的处理方法,可自适应地将一个复杂的多分量非平稳信号分解成若干个乘积函数(PF)之和[10],其中每一个PF分量都是一个纯调频信号和一个包络信号的乘积。在经典的LMD方法中,采用滑动平均法得到的局部均值函数和包络估计函数会发生较明显的相位偏移现象。为解决上述问题,本文采用三次样条插值法进行平滑处理,LMD分解过程如下。
①找出原始信号x(t)的所有极值点并排序,分别对左、右端的极值点进行镜像延拓[11],从而得到 延 拓 后 的 序 列x'(t)。
②对所有的极值点分别进行三次样条插值,得到上包络线Eup和下包络线Edown。
③通 过 式(1)和 式(2)求 出 局 部 均 值 函 数m11(t)和 包 络 估 计 函 数a11(t)。
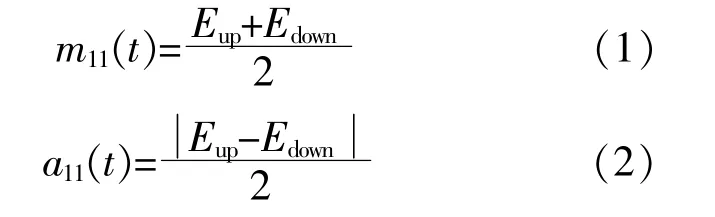
④将m11(t)从 原 始 信 号x'(t)中 分 离 出 来,得到 剩 余 量h11(t),对h11(t)进 行 解 调,得 到 调 频 信号s11(t)。
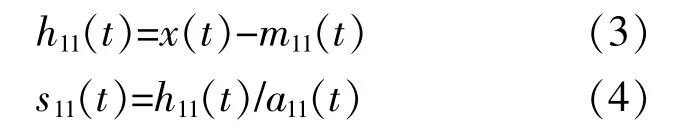
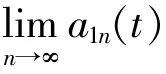
⑥将上述过程中产生的所有包络估计函数相乘,得 到 包 络 信 号a1(t)。将a1(t)和s1n(t)相 乘,得到 信 号x'(t)的 第 一 个PF分 量。
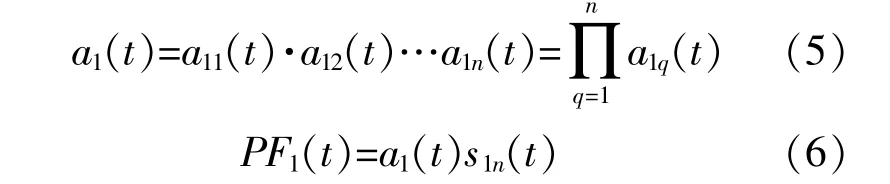
PF1(t)的 瞬 时 频 率f1(t)可 由s1n(t)求 出:
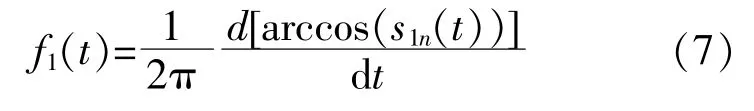
⑦将PF1(t)从 原 始 信 号x'(t)中 分 离 出 来,得到 一 个 新 信 号u1(t)。对u1(t)重 复 上 述 步 骤k次,直到uk(t)为常数或一个单调函数为止。
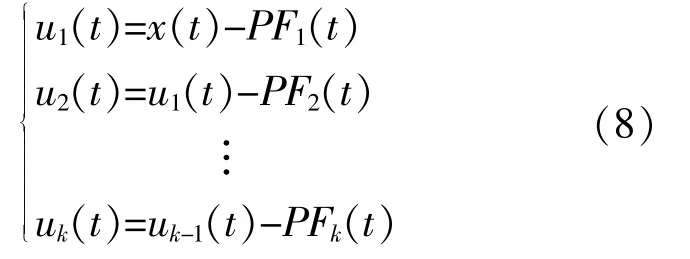
至此,将原始信号分解为k个PF分量和一个剩余分量uk之和。
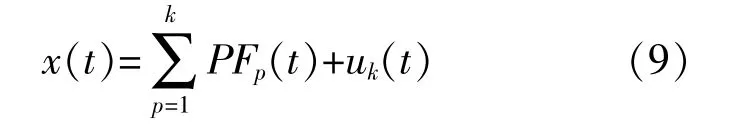
2 基于LMD-IMVO-LSSVM的风速预测模型
2.1 LSSVM及核函数选择
LSSVM是对支持向量机(SVM)的一种改进,将QP问题转化为求解线性方程组问题,将不等式约束变为等式约束,从而方便了Lagrange乘子alpha的求解,提高了收敛速度[12]。对于给定训练集:
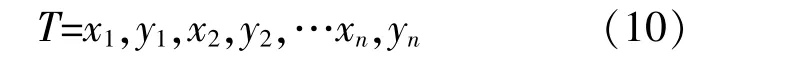
假设其回归函数为

式中:x为样本输入;y为样本输出;ω和b分别为高维空间中超平面的法向量和截距。
根据风险最小化原则,回归问题可以转化为约束问题。
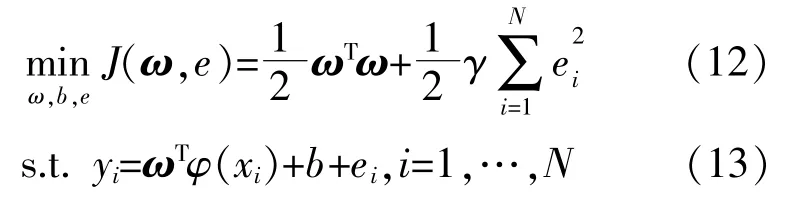
式中:ei为松弛变量;γ为正则化因数。
引入Lagrange乘子α,上述问题转化为
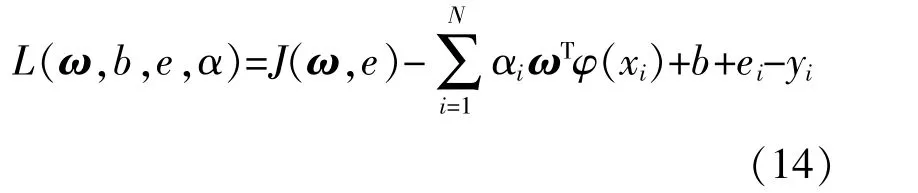
分 别 对 ω,b,e,α求 偏 微 分,得 到 最 优 值,进而建立回归函数:
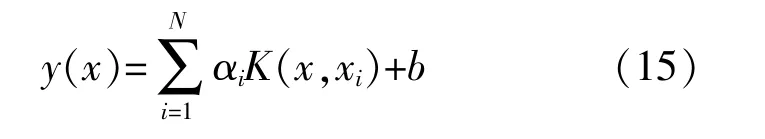
式 中:K(x,xi)为 核 函 数。
在用LSSVM进行风速预测时,核函数类型对LSSVM回归性能有很大的影响。LSSVM常用的核函数有线性核函数、径向基核函数、多项式核函数和傅里叶核函数等。文献[13]通过对不同核函数的仿真分析,得出径向基核函数的预测精度较高,因此本文选用径向基核函数,其表达式为
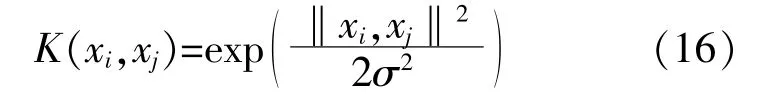
式中:σ为核宽度。
惩罚因子 γ和 σ是影响LSSVM预测性能的主要参数,为提高模型的预测精度,本文采用改进多元宇宙算法寻优这两个参数,来提高风速预测精度。
2.2 MVO
MVO是Seyedali Mirjalili受到多元宇宙理论的启发提出来的元启发式优化算法[14]。主要根据多元宇宙理论的3个主要概念-白洞、黑洞和虫洞,来建立数学模型。
MVO算法中的可行解对应宇宙,解的适应度对应该宇宙的膨胀率,在每一次迭代中,根据膨胀率对宇宙进行排序,通过轮盘赌随机选定一个宇宙作为白洞,宇宙间通过黑、白洞进行物质交换。假定:
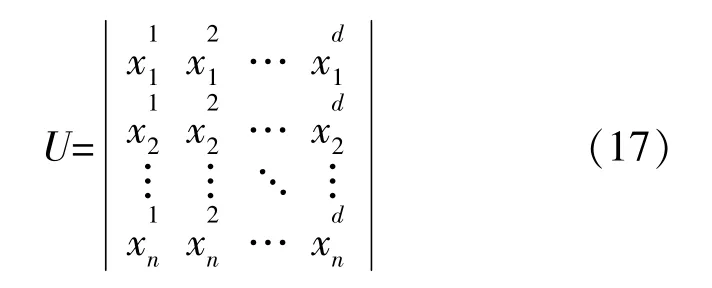
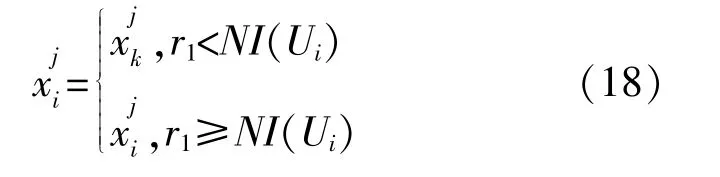
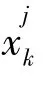
宇宙之间通过虫洞随机传送物质以保证种群多样性,同时都与最优宇宙交换物质以提高膨胀率。
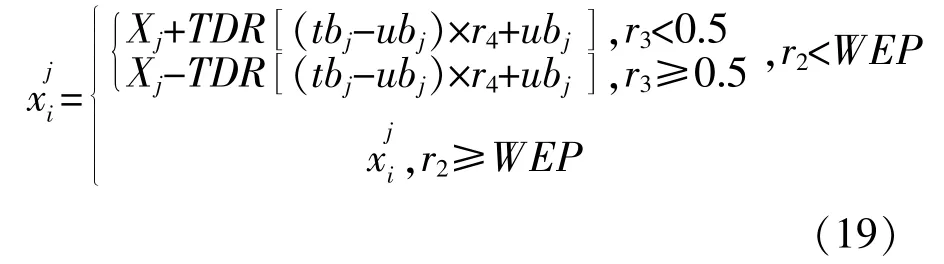
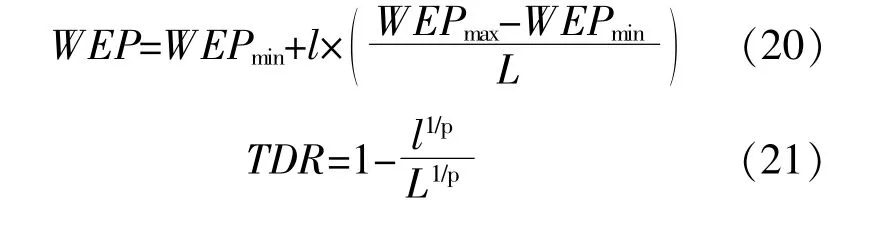
WEP和TDR均为MVO的重要参数。式中:WEPmax和WEPmin分别为参数WEP的上、下界,取0.2和1;l和L分别为当前迭代次数和最大迭代次数;p为算法的开发精度,取6。
MVO算法的优化进程始于种群的随机初始化,通过多个宇宙的并行迭代搜索,最终得到问题的近似最优解。
2.3 IMVO
MVO算法主要依靠虫洞进行穿越寻优,在最优宇宙附近进行旅行,TDR是影响算法性能的重要参数,但MVO中的TDR变化幅度较为单一,不能同时满足精确与高效的要求。由MVO的定义可知,TDR值较大时可提高全局探索能力,TDR值较小时可增强局部深度开发,因此,为实现在迭代前期保持较快的迭代趋势进行全局探索,迭代后期保持较慢的迭代趋势进行局部开发的要求,本文提出新的旅行距离率TDR。
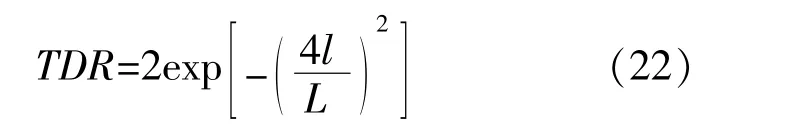
同时,为了更有效地找出所优化参数的最大范围,对全局变量更新机制进行改进,当l>L/2时,开始使用新的变量更新机制。
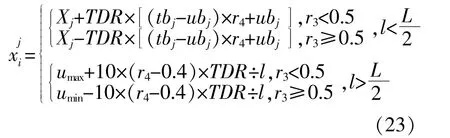
改进的变量更新方法有两个主要特点:一是只在当前最优解的最大值和最小值附近搜索;二是新机制下,变量更新不再依赖宇宙边界tbj和ubj。这使得在处理包含大量数据的预测问题时,算法优化更快,更加突出对参数的搜索。
IMVO算法运行流程如下:
①定 义各参数,包括宇 宙维 度d,n,WEP,L,tbj和ubj等;
②初始化多元宇宙种群U;
③根据式(19)执行轮盘赌机制;
④计算各宇宙的膨胀率,确定当前最优宇宙;
⑤根 据 式(20),(22)更 新WEP和TDR;
⑥根据式(23)更新最优宇宙,优于当前最优宇宙时将其替换,反之则保留当前最优宇宙;
⑦判断是否最大迭代次数,是,终止循环,输出最优宇宙和目标函数值;反之,则迭代次数加1,跳转至③继续循环。
IMVO算法流程如图1所示。

图1 IMVO算法流程图Fig.1 Flow chart of IMVO algorithm
2.4 基于LMD-IMVO-LSSVM的风速预测方法
风速时间序列具有非线性、随机性和不稳定性,直接对风速时间序列进行预测难以获得精准的预测结果。
本文利用LMD对风速信号进行分解,采用IMVO优化LSSVM模型的2个参数,从而建立了LMD-IMVO-LSSVM的风速预测模型,具体方法如下:
①对数据整理分析并归一化处理,得到原始风速序列;
②对原始风速序列进行LMD分解,得到从高频到低频的一系列PF分量和uk;
③对分解得到的每个分量,分别建立IMVOLSSVM模型,以每个子序列的平均绝对误差作为目标函数值,采用改进多元宇宙算法优化γ和σ这两个参数,并进行风速预测;
④叠加不同频率下的风速预测序列,形成最终的风速预测值;
⑤误差分析。
LMD-IMVO-LSSVM的预测流程如图2所示。
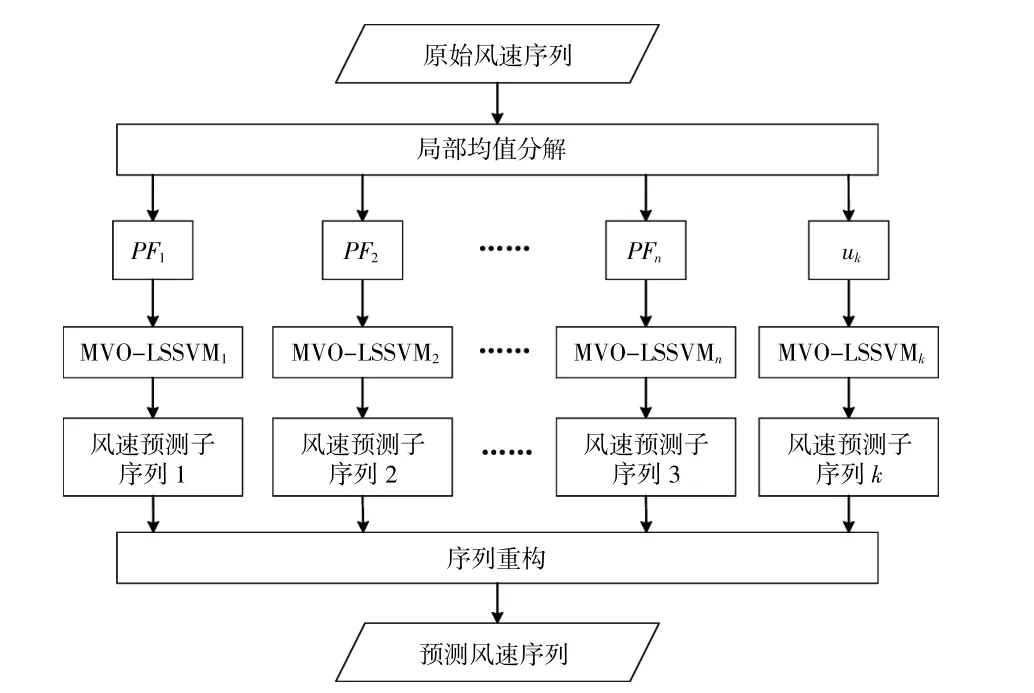
图2 基于LMD-IMVO-LSSVM的风速预测流程图Fig.2 Flow chart of wind speed prediction based on LMD-IMVO-LSSVM
3 算例分析
3.1 算例说明
本文原始数据选自新疆某风电场的实测数据,采样间隔为15 min,共采取了600个样本点,采取的风速时间序列曲线如图3所示。取前500个样本点作为训练集,后100个样本点作为测试集。
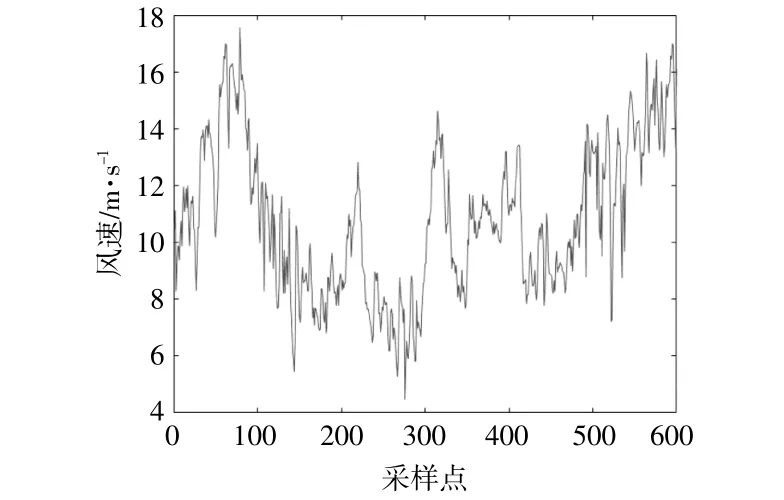
图3 新疆某风电场风速实测曲线Fig.3 Wind speed measurement curve of a wind farm in Xinjiang
根据《NB/T31046-2013风电功率预测系统功能规范》,本文选取均方根误差(RMSE)和平均绝对误差(MAE)作为预测结果的评价指标。
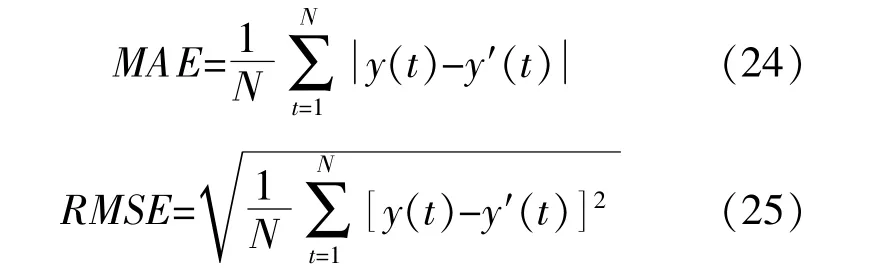
式 中:N为 采 样 点 数;y(t)为t时 刻 的 预 测 值;y'(t)为t时刻的实际值。
3.2 LMD分解结果
对采集的600个风速样本点进行LMD分解,分解得到4个PF分量和一个uk,分解曲线如图4所示。
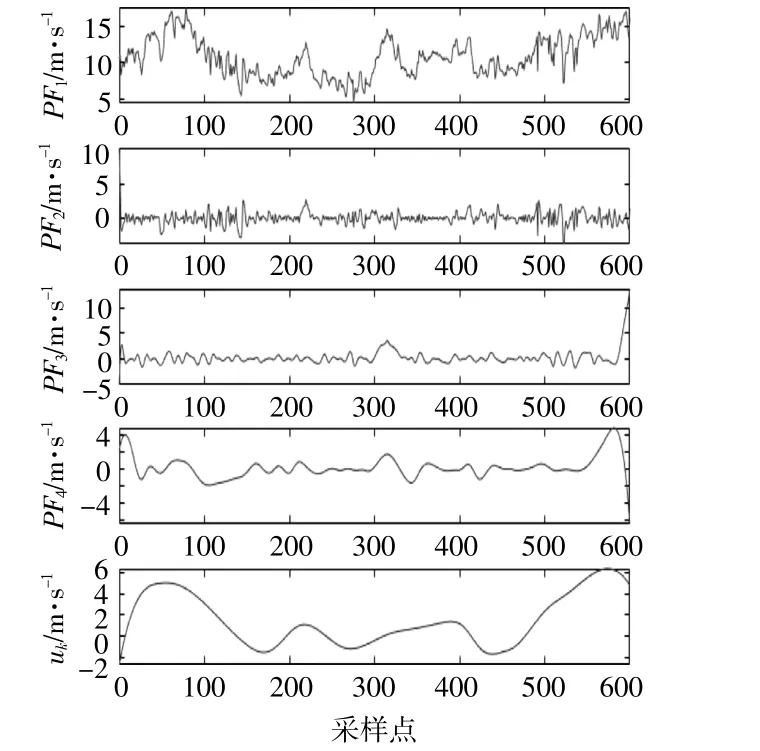
图4 LMD分解曲线Fig.4 LMD decomposition curve
由图4可知:uk主要反映了风速曲线的基频扰动,其变化规律与图3的变化规律基本一致;PF4主要反映uk上的局部扰动,体现了局部风速的变化规律;PF2及PF3分量反映出风速序列中包含的低频、高频均值为零的随机风速信息,其幅值波动大小反映瞬时风速变化程度;PF1分量反映平均风速信息,其风速约为10 m/s。
3.3 预测结果分析
采用IMVO算法优化预测模型中精度受到影响的2个参数,设置 γ和 σ的寻优范围为(0.1,1 000),将分解后每个子序列训练的MAE作为优化目标函数,IMVO算法优化模型参数的值如表1所示。
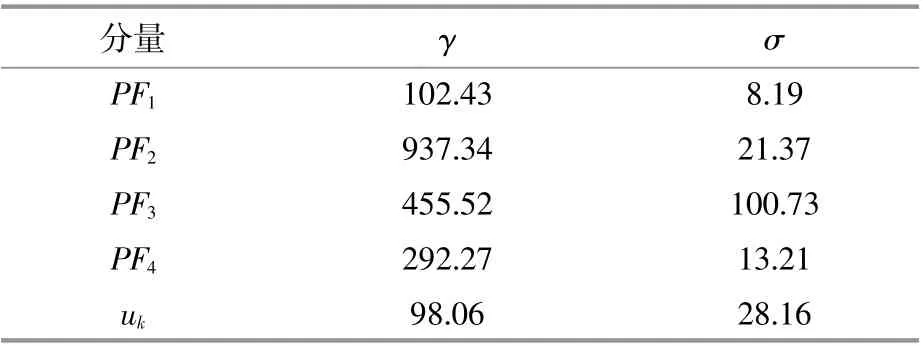
表1 IMVO的参数寻优结果Table 1 The parameter optimization results of IMVO
原始风速时间序列经过LMD分解得到了4个PF分量和1个剩余分量,采用改进的MVO算法对LSSVM参数进行寻优,最终建立了一种LMD-IMVO-LSSVM的风速预测模型。为验证所提模型的预测精度,本文还分别对LSSVM模型、LMD-LSSVM模型、LMD-PSO-LSSVM模型和LMD-MVO-LSSVM模型进行风速预测,预测结果如图5所示。

图5 风速预测结果Fig.5 Wind speed prediction results
由图5可知:利用LSSVM直接进行预测时,对于风速波动不敏感,且误差相对较大;LMD方法分解出多种频率的风速信息,能增加预测的准确性,但未经算法优化的LMD-LSSVM只能大致符合风速序列的基频波动,在面对短时风速波动时仍然存在较大的误差;经过LMD方法分解后,由PSO,MVO和IMVO 3种优化算法对LSSVM核函数优化后的LSSVM不仅能有效地预测出风速序列的基频波动,其局部波动也能被准确地预测,能够有效对原始的风速曲线进行拟合。
对本文所建立的5种预测模型进行误差分析,误差指标如表2所示。
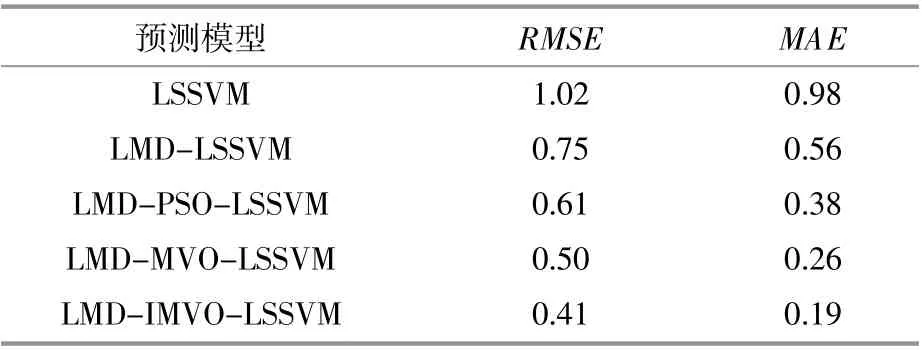
表2 5种模型误差评价指标Table 2 5 model error evaluation indexes
由表2可知,IMVO优化的LSSVM模型RMSE误差为0.41,MAE误差为0.19,在5种模型中误差指标最小。该结果验证了IMVO算法具有较好的寻优能力,适用于径向基核函数的寻优过程。
4 结论
本文利用IMVO算法对LSSVM参数进行寻优,结合LMD数据分解方法,提出了一种基于LMD-IMVO-LSSVM的风速预测模型。通过仿真实验对比分析,得出以下结论。
①针对风速时间序列具有随机性的特点,利用LMD提取出的不同特征信息进行预测,消除了模态混叠现象,可有效提高预测精度。
②寻优结果表明,IMVO算法的全局寻优能力优于MVO和PSO算法。
③利用IMVO算法对LSSVM参数进行寻优,通过对比分析,发现本文提出的LMD-IMVOLSSVM预测模型的预测精度更高,预测结果也更加贴合实际数据。
