一种永磁同步电机无位置传感器混合控制策略

石高峰，彭再武，凌岳伦，蔡 磊，陈慧民，胡振球

（1.长沙中车智驭新能源科技有限公司，湖南 长沙 410000；2.中车时代电动汽车股份有限公司，湖南 株洲 412007）

0 引言

永磁同步电机(permanent magnet synchronous motor，PMSM)由于其高功率密度、高效率和高可靠性等性能优点在船舶推进、铁路列车和电动汽车等交通工具上都获得了广泛的应用。如电动汽车的电液助力转向系统（electro-hydraulic power steering system，EHPS）多采用永磁同步电机，通过调节油泵电机转速、控制液压泵的流量，从而产生合适的液压力，为转向系统提供辅助动力。由于EHPS的运行工况简单，其永磁同步电机基本以恒定的额定频率工作，常采用无位置传感器控制策略。这样既能降低系统的成本和复杂性，也可以提高系统的可靠性。

目前，无位置传感器控制策略根据电机速度范围可以分为两种：适用于零速和低速（简称“零低速”）的方法和适用于中高速的方法。零低速区，PMSM无位置传感器控制主要采用高频方波信号注入法[1]、脉振高频信号注入法[2]、旋转高频信号注入法[3]及 INFORM 法[4]等；而中高速区，采用基波模型估算电机转子位置和转速，包括反电动势法[5]、滑模观测器法[6]、扩展卡尔曼滤波器法[7]及模型参考自适应观测器法[8]等方法。

中高速PMSM无位置传感器控制方法需要直接或间接依赖永磁同步电机旋转反电动势，通常转速需要高于10%额定转速，这样才能获得准确的估算位置。由于零低速下永磁同步电机的反电动势不够大，导致中高速下的位置估算方法在低速时的位置估算误差较大，所以目前常用的零低速方法主要利用电机凸极特性提取转子位置信息。然而低速区普遍采用的高频信号注入法除了会产生额外的损耗和高频振动噪声外，还需要进行大量的运算，占用较多的控制器资源。研究人员把基本的电流闭环、速度开环的控制方法（IF控制）[9]用在中高速无位置传感器控制的电机起动阶段；当电机转速较高时，切换到基波模型观测器上，需要重点解决IF控制与观测器法控制的切换策略，实现电机的平稳起动和稳定运行。

本文通过将IF控制策略和扩展反电动势观测器有机结合，提出一种可在宽调速范围内工作的无位置传感器混合控制策略：电机在低速区，可采用转速开环、电流闭环的IF控制策略；在高速区，采用扩展反电动势观测器估计转子转速与位置；在过渡区，采用转矩角闭环调节电流方法，实现永磁同步电机的平稳起动和控制策略的平滑切换。最后，在一台EHPS用永磁同步电机上对所提混合控制策略进行了实验验证。

1 基于扩展反电动势的转子位置估算

永磁同步电机在中高速运行时，容易得到定子绕组的电流和反电动势信息，根据电机的基波模型就能获取准确的转子估算位置。另外，扩展反电动势模型结构简单，还包含位置信息，非常适用于无位置传感器控制。

由旋转坐标系下永磁同步电机的扩展反电动势模型可得到静止坐标系下的电机模型[10]：

其中，eα=-Esinθr,eβ=Ecosθr，E=ωrψr+(Ld-Lq)(ωrid-piq)。式中：uα——α轴的电压；uβ——β轴的电压；iα——α轴的电流；iβ——β轴的电流；id——d轴的电流；iq——q轴的电流；Ld——d轴的电感量；Lq——q轴的电感量；ψr——永磁体的磁链；Rs——定子的电阻；ωr——转子的电频率；θr——转子的电角度；E——扩展反电动势幅值；eα——α轴的扩展反电动势；eβ——β轴的扩展反电动势；s——拉普拉斯算子。

由于扩展反电动势无法通过测量得到，可将电流的估计值和测量值求差，再经过PI调节器求得反电动势的估计值。扩展反电动势观测器的原理如图1所示。下面推导估算反电动势与电机模型反电动势之间的关系，其中上标“˄”表示估计值。

图1 扩展反电动势观测器Fig. 1 Extended back EMF observer

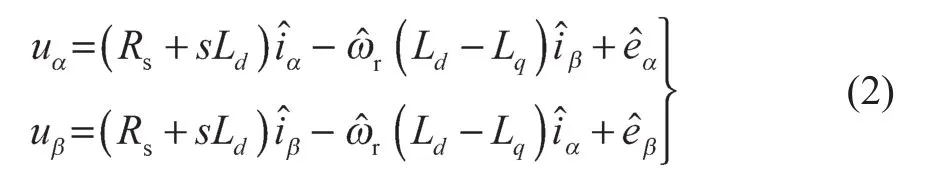
其中，

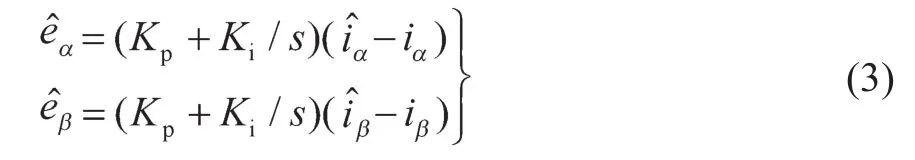
式中：Kp——PI的比例系数；Ki——PI的积分系数。

由式(1)～式(3)可以推导出估算的扩展反电动势与真实的扩展反电动势的关系：

式中：eαβ——扩展反电动势的复矢量；——估算的扩展反电动势复矢量。

观测反电动势后，一般可用式(7)直接计算转子电角度。由于反正切函数计算角度容易引入抖动且存在过零点问题，因此本文使用反电动势归一化的正交锁相环提取转子电角度，其中锁相环控制参数Kp=150，Ki=5 625。此时锁相环系统有较好的动态响应，锁相环原理如图2所示。

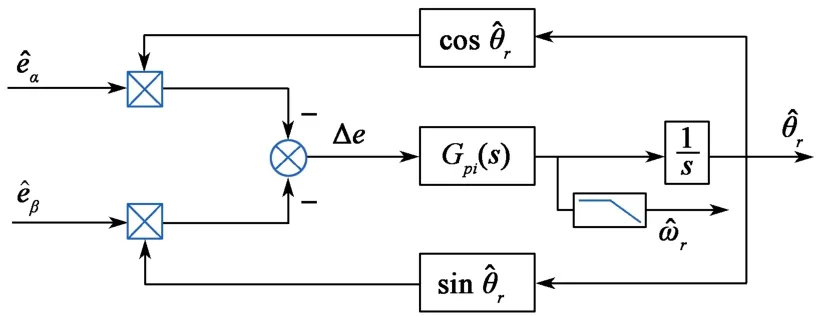
图2 锁相环原理框图Fig. 2 Block diagram of phase-locked loop

2 转矩角计算及闭环控制

要实现从转速开环到转速闭环的切换，需要设计一种恰当的切换策略。目前切换方案主要分为两类：一类是采用加权融合方案[11]，主要适用于低速、使用转速观测器的场合；另外一类是通过减小电流幅值实现转矩角逼近，主要适用于低速、采用开环启动的场合[12-13]。减小电流幅值、实现转矩角逼近0.5π的方法属于间接转矩角控制。该方案需要恰当设置电流下降斜率，且需要兼顾两种坐标系的相位差；若参数设置不当，极易引起切换失败。为克服间接转矩角控制的不足，本文提出一种直接转矩角控制方案，实现开环启动到闭环控制的平稳过渡。该方案通过电机的瞬时功率估算出转矩角，并构建转矩角的闭环调节器以实现电机电流幅值的自动调节。该融合方案与低速IF开环控制一样，均属于转速开环控制，区别在于电流指令值给定不同。下面对转矩角闭环控制方案的原理进行分析。图3给出了转速开环下γδ坐标系的示意图，其中定子电压矢量us与电流矢量is夹角为ε，表示功率因数角；δ轴与d轴夹角为δ，表示转矩角。

图3 γδ坐标系示意图Fig. 3 γδ coordinate system diagram

在γδ坐标系下，PMSM瞬时功率计算如下：

式中：uγ——γ轴电压；uδ——δ轴电压；iγ——γ轴电流；iδ——δ轴电流；P——有功功率；Q——无功功率。

对于表贴式永磁同步电机，由于定子电流落在δ轴，因此有iγ=0，iδ=is，γδ坐标系下 PMSM 稳态电压方程为

式中：Ls——定子电感；is——定子电流。

由式(10)可计算转矩角：

对于凸极式电机，d轴、q轴电感存在差异，用式(11)计算的转矩角存在误差，需要重新推导瞬时功率关于转矩角的表达式。对式(8)进行坐标变换，有

由于变换矩阵Tγδ/dq为单位矩阵，该变换属于等功率变换，由式(8)和式(12)可以推导出

对于表贴式和凸极式电机，估算转矩角具有相同的表达式，转矩角计算示意过程如图4所示。为保证电机能顺利切换到转速闭环控制，选取转矩角指令值δ*=1.55 rad。其中转速开环控制中的坐标变换角由给定转速积分获得，如

图4 转矩角计算示意图Fig. 4 Schematic diagram of torque angle calculation

式中：θopen——开环控制的电角度；——开环控制给定的电频率。

3 全速区间无位置传感器控制策略

本文中全速区间永磁同步电机无位置传感器的控制策略如图5所示。根据电机速度，控制过程分为3个阶段。

图5 全速区间无位置控制策略Fig. 5 Position sensor-less control strategy in full speed zone

第Ⅰ阶段（Flag=0），采用转速开环、电流闭环的IF控制策略。此阶段以参考速度指令当作控制速度，控制位置由给定转速积分计算得到，d轴参考电流为0 A，q轴参考电流为额定电流，即i*δ=IN。

第Ⅱ阶段（Flag=1），仍旧采用转速开环、电流闭环IF控制策略。此阶段仍以参考速度指令当作控制速度，控制位置也仍由给定转速积分计算得到。但是q轴参考电流是在第Ⅰ阶段电流的基础上叠加一个电流调节量，该调节电流幅值由转矩角闭环控制计算而得，即实际q轴参考电流为i*δ。通过转矩角闭环控制，q轴参考电流逐渐达到与负载相匹配的幅值。

第Ⅲ阶段（Flag=2），采用转速闭环、电流闭环的双闭环控制策略。此阶段控制速度和控制位置由基于扩展反电动势算法估算。实际q轴参考电流由速度环闭环控制计算得到。为实现第Ⅱ阶段到第Ⅲ阶段的平滑过渡，速度环PI的积分初始值应为第Ⅱ阶段的参考电流。如果使用凸极永磁同步电机，也可以按照MTPA曲线进行d轴、q轴电流指令值分配。

综上，本文所提全速区间无位置控制策略关键在于：（1）电机转矩角计算；（2）转速由开环控制向闭环控制切换。（3）转速闭环阶段的转速估算和位置观测。

4 实验验证

建立实验平台验证本文所提的控制策略，以EHPS用永磁同步电机作为实验对象，其参数如下：额定功率pN=4.0 kW，极对数NP=4，定子相电阻Rs=0.75 Ω，电感Ls=13.1 mH，永磁磁链ψr=0.3 Wb，额定转速Nr=1 000.0 r/min，额定电流幅值Is=16.0 A，额定电角频率ωr=418.0 rad/s，转动惯量J=0.005 kg·m2，逆变器直流侧电压Udc=540.0 V。

本实验过程由4个阶段组成,第Ⅰ阶段为预定位，从0.0 s时刻到1.0 s时刻，预定位参考电流为10.0 A；第Ⅱ阶段采用IF控制起动，从1.0 s时刻到3.0 s时刻，起动参考电流为22.0 A，转速按照线性增加，过渡点设置在30%额定转速（300.0 r/min）；第Ⅲ阶段为转速开环到转速闭环的切换，从3.0 s时刻到5.4 s时刻，在IF控制的最大参考电流基础上叠加由转矩角闭环控制的电流调节量。随着转速的增加，切换点设置在70%额定转速（700.0 r/min）位置，此时控制策略由IF控制切换到基于扩展反电动势估算的速度闭环控制；第Ⅳ阶段为基于扩展反电动势估算的速度和电流闭环控制，从5.4 s时刻到8.0 s时刻，电流指令为转速PI控制器的调节量，速度和位置信号由扩展反电动势估计算法计算得出。为了验证本文所提IF控制到闭环控制的切换策略效果，实验中，速度过渡起点设定为30%额定转速，切换点设定为70%额定转速。在实际应用中，过渡点和切换点速度均小于这两个设定阈值。

空载起动过程如图6～图9所示。为了避免IF控制在中高速阶段存在带载能力不足以及在零低速阶段下扩展反电动势估算误差偏大的问题，本文在过渡阶段直接采用转矩角闭环控制调节q轴参考电流，以实现控制方式切换过程电机电流平滑无冲击。

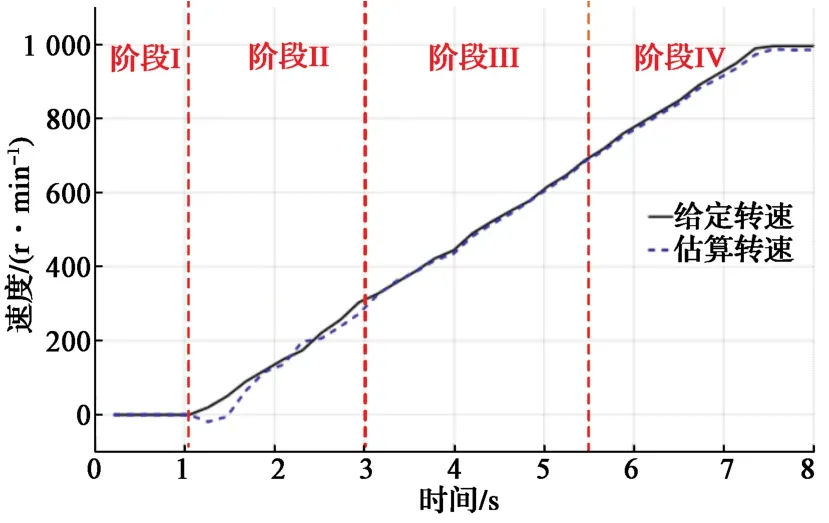
图6 空载起动的速度波形Fig. 6 Speed waveforms of PMSM starting without load

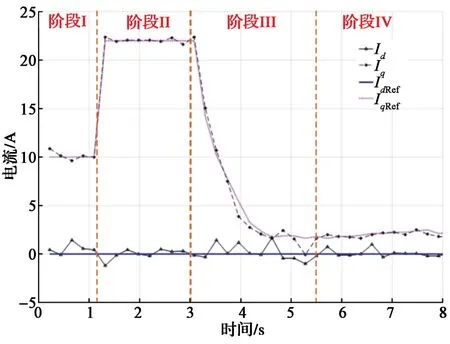
图7 空载起动的电流响应波形Fig. 7 Current response waveforms of PMSM starting without load

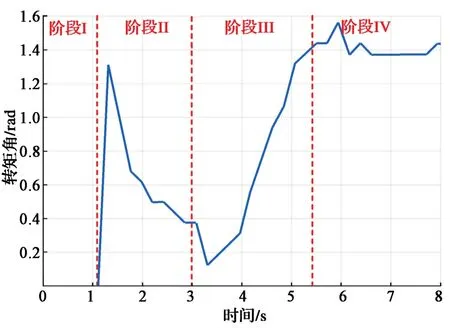
图8 空载起动的转矩角计算波形Fig. 8 Torque angle calculation waveforms of PMSM starting without load

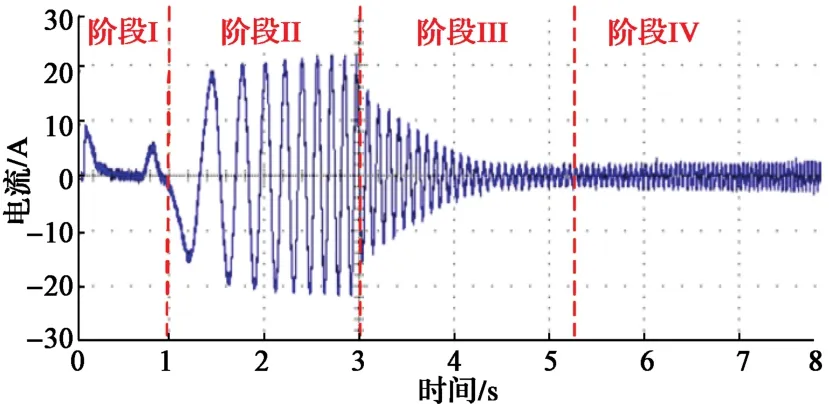
图9 空载起动的定子电流波形Fig. 9 Stator current waveforms of PMSM starting without load

从图6和图7可以看出，在30%额定转速以下（阶段Ⅱ）时，IF控制采用最大电流起动，转矩角实时计算；当转速达到30%额定转速时（阶段Ⅲ），转矩角闭环控制起作用，在转矩角闭环控制过程中，实际转矩角逐步达到计算的参考值1.55 rad，同时q轴参考电流从最大值逐步减小到与负载相匹配的最优电流值（空载电流幅值约为2.0 A）；当转速达到70%额定转速时（阶段Ⅳ），系统控制策略切换为基于扩展反电动势算法的转速和电流闭环控制。从图6中可以看出，电机能够平顺地从速度开环运行状态向速度闭环运行状态过渡，其速度过渡平稳；从图9中的电机相电流波形可以看出，在系统的整个起动过程，电机定子电流幅值和频率自动调节，没有出现冲击现象；到达稳态时，定子的实际电流达到负载平衡所需的电流。

带载起动过程如图10～图13所示，可以看出，在第Ⅲ阶段即过渡阶段，采用转矩角闭环控制调节q轴参考电流，增强IF低速带载运行的鲁棒性，电流幅值和频率自动调节，且没有出现失步和转速振荡等现象。图11中，q轴电流从最大电流平滑过渡到负载电流（约14.0 A），并且在q轴电流下降的后期进行控制策略切换，能够获得非常平顺的过渡效果。从图13和图14的定子电流波形可以看到，从带载起动到稳定运行的完整过程，实际定子电流无冲击现象，定子电流幅值和频率自动调节，过渡曲线平滑。比较图8与图12的转矩角计算波形和响应，可以看出，带载情况的优于空载情况的。

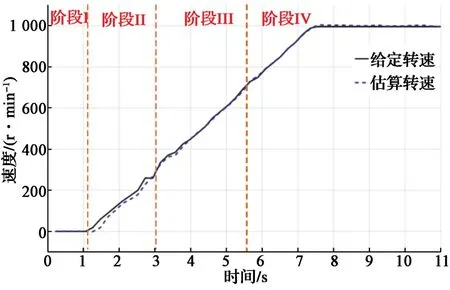
图10 带负载起动的速度波形Fig. 10 Speed waveforms of PMSM starting with load

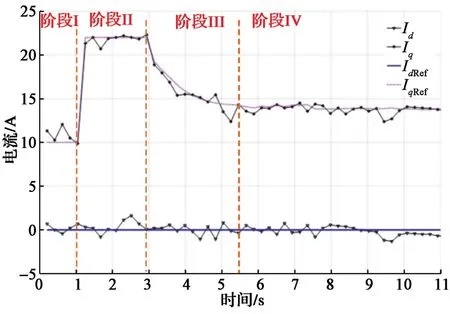
图11 带负载起动的电流波形Fig. 11 Current waveforms of PMSM starting with load

图12 带负载起动的转矩角计算波形Fig. 12 Torque angle calculation waveforms of PMSM starting with load

图13 带负载起动的定子电流波形Fig. 13 Stator current waveforms of PMSM starting with load

图14 带负载稳态运行的定子电流放大波形Fig. 14 Stator current amplification waveforms of PMSM with load in steady state operation

5 结语

电液助力转向系统用永磁同步电机的基本工况是在额定频率下负载突增突减，但也经常出现零低速带载起动的情况。为此，将IF控制策略和基于扩展反电动势观测器的无位置传感器控制进行有机结合，以满足系统实际工况需求。本文所提控制策略的主要特点是在控制策略切换过程中，采用转矩角闭环控制调节电流指令，增强IF控制策略的带载能力，并实现电机从速度开环运行状态向速度闭环运行状态平稳切换，以及实现速度和电流的平滑无冲击过渡。实验数据表明，采用转矩角闭环调节q轴电流的策略，实现了电机的平稳起动，起动过程电流没有过冲现象；并且增强了IF在中高速阶段带载能力，保证了电机电流幅值和频率的自动调节。本文所提混合控制策略在空载和带负载的工况下都表现出稳定、准确和快速的控制性能。反馈转矩角的计算需要用到q轴电感Lq，所以在实际系统匹配中要合理选取Lq，通常借助电机参数辨识算法进行获取。为了实现转矩角的精确估算，后续将进一步深入研究永磁同步电机参数辨识。