分离变量法求解二维平面薄板相关问题的研究

屈恩相，齐 辉，杨 杰，王 丽，邓 琳，乔 雪，郭丽婷

(1.齐齐哈尔大学 建筑与土木工程学院，黑龙江 齐齐哈尔 161006；2.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；3.上海电机学院 机械学院，上海 201306)

板作为工程结构常用的构件之一，常常作为分析问题的研究对象。比如建筑工程中的楼板、悬挑板、桥面板；海洋工程结构中的外板、甲板；水利工程中的水闸闸门等等。研究板结构的力学性能及破坏机理对于工程安全稳定具有重要意义。实际上，板的应力、应变、位移的计算问题属于弹性力学的空间问题。在数学上处理板所满足的微分方程和边界条件精确解的问题存在很大困难。分离变量法的应用研究已经非常广泛[1-2]，不仅仅应用在求解数学问题的微分方程[3-4]，也广泛对的应用在力学学科上。比如涉及到力学中的弹性地基薄板振动[5-8]、电磁场方程的分析[9-11]、量子力学[12]、波动方程[13]、航天器最优转弯问题[14]、非理想反激变换器模型推导[15]、非线性动力学[16-18]等问题上分离变量法都得到了很好地应用，这些都为理论研究提供很好的借鉴。围绕二维平面薄板所满足给定边界条件的偏微分方程的求解展开研究，采用数学物理方程中的分离变量法对薄板所满足的偏微分方程进行变量分离，将偏微分方程转化常微分方程，从而有效的解决该问题。由文献[19-23]可知，分离变量法的求解过程可以总结如下。

(1)构造所求的解形式以W(x,y)=X(x)Y(y)为类似的形式代入偏微分方程中，将相对应变量进行分离，得到两个常微分方程。

(2)根据已知的W(x,y)边界条件，导出X(x)所满足的边界条件，从而得到该变量符合的常微分方程的特征值问题。

(3)求解该特征问题所决定的特征值λm及相应的特征函数Xm(x)。

(4)决定所对应的Ym(y)形式。

1 板的定义及介绍

图1 平板模型图

板在弹性力学中是这样规定的：两个平行平面和垂直平行面的柱面或者棱柱面所围成的物体，当高度远小于底面尺寸时为平板(简称板)，平板模型图如图1所示。两平行面称为板面，垂直于板面的柱面或者棱柱面称为板边，两平行面之间的距离称为板厚，平分板厚的平面称为中面。按照板的厚度和受力可以分为薄板、膜板、厚板，平板的分类如表1所示。采用分离变量法分析的是薄板的二维平面小挠度问题。

表1 平板的分类

2 二维平面薄板边界条件

二维平面薄板的边界主要存在固定边界、简支边界、自由边界三种不同的情况如图2所示。

图2 二维平面薄板边界存在形式

其中OA为固定边界、AB和BC为自由边界、OC为简支边界，不同边所满足的边界条件可以整理成如表2所示。

表2 平面薄板边界条件及表示

3 求解矩形薄板振动问题

二维平面直角坐标系所建立矩形薄板的模型如图3所示，其中矩形薄板四条边界为自由边界。

图3 矩形薄板振动问题的二维平面图

边界条件可以表示为

角点条件表示为

弹性矩形薄板横向振动方程可以表示如式(1)所示。

(1)

令W(x,y)=X(x)Y(y)代入式(1)，进一步整理成如式(2)所示。

(2)

3.1 变量X(x)解的分离情况

将式(2)两边同时除以X(x)Y(y)，对y求导一次将相同变量结合在一起，并令其等于常数-α2可以得到，如式(3)所示。

(3)

将式(3)变量分离后可以进一步整理成如式(4)所示。

X″(x)+α2X(x)=0

(4)

3.1.1 系数α取值的分类讨论

第一种为系数α=0，可以得到X(x)=A1+A2x代入式(2)得如式(5)所示。

YⅣ(y)-γ4Y(y)=0

(5)

式(5)特征根有四种情况γ,-γ,iγ,Y(y)，解的形式可以表示如式(6)所示。

Y(y)=B1sinhγy+B2coshγy+

B3sinγy+B4cosγy

(6)

第二种为系数α≠0，X(x)=C1sinαx+C2cosαx代入式(2)可得如式(7)所示。

YⅣ(y)-2α2Y″(y)+(α4-γ4)Y(y)=0

(7)

Y(y)=D1sinhα1y+D2coshα1y+

D3sinα2y+D4cosα2y

(8)

Y(y)=D1sinhα1y+D2coshα1y+

D3sinhα3y+D4coshα3y

(9)

3.2 变量Y(y)解的分离情况

将式(2)两边同时除以X(x)Y(y)，对x求导一次将相同变量结合在一起，并令其等于常数-β2，又可以得到另一个变量整合形式如式(10)所示。

(10)

将式(10)变量分离后进一步整理可以得到如式(11)所示。

Y″(y)+β2Y(y)=0

(11)

3.2.1 系数取值β的分类讨论

第一种为系数β=0，可以得到Y(y)=E1+E2y代入式(2)得如式(12)所示。

XⅣ(x)-γ4X(x)=0

(12)

式(12)特征根有四种情况γ，-γ，iγ，-iγ。Y(y)解的形式可以表示成如式(13)所示。

X(x)=F1sinhγx+F2coshγx+

F3sinγx+F4cosγx

(13)

第二种为系数β≠0，Y(y)=G1sinβy+G2cosβy代入式(2)得如式(14)所示。

XⅣ(x)-2β2X″(x)+(β4-γ4)X(x)=0

(14)

方程特征根又分为两种情况。第一种情况是γ>β时，方程的根有四个分别为β1，-β1，iβ2，-iβ2。

X(x)=H1sinhα1x+H2coshα1x+

H3sinα2x+H4cosα2x

(15)

X(x)=H1sinhβ1x+H2coshβ1x+

H3sinhβ3x+H4coshβ3x

(16)

通过对矩形薄板边界自由振动问题为例，使用分离变量法分别对X(x)和Y(y)的解进行变量分离并讨论，能够清晰分析出偏微分方程混合问题经过变量分离，转化为常微分方程的初值问题的应用过程。

4 求解矩形薄板波动问题

图4 矩形薄板波动问题的二维平面图

如图4所示分析的是边界条件为固定边界的二维平面薄板，采用分离变量法来研究该类问题波动方程解的形式。二维波动方程可以表示如式(17)所示，边界条件可以表示如式(18)所示，初始条件如式(19)所示。

(17)

(18)

(19)

设u(x,y,t)=F(x,y)G(t)将其代入式(17)得如式(20)所示。

F(x,y)G″(t)=c2[FxxG(t)+FyyG(t)]

(20)

式(20)两边同时除以F(x,y)G(t)，并令等式右端为一常数-υ2整理得如式(21)所示。

(21)

式(21)进一步化简整理得如式(22)所示。

(22)

式(22)中关于G(t)的函数进一步移项整理得如式(23)所示。

G″(t)+υ2c2G(t)=0

(23)

令λ=υc代入式(23)得如式(24)所示。

G″(t)+λ2G(t)=0

(24)

将式(22)中关于变量x和y的函数进一步移项整理得如式(25)所示。

Fxx+Fyy+υ2F(x,y)=0

(25)

令F(x,y)=H(x)Q(y)，代入式(25)中，进一步整理成如式(26)所示。

(26)

将式(26)移项整理得如式(27)所示。

(27)

(28)

式(28)中对变量x项进行整理如式(29)所示。

(29)

式(29)的二阶齐次线性微分方程的解如式(30)所示。

H(x)=Acoskx+Bsinkx

(30)

将式(28)中关于变量y项进行整理如式(31)所示。

(31)

令p2=υ2-κ2代入到式(31)进一步整理成如式(32)所示。

(32)

式(32)的解可以表示成如式(33)所示。

Q(y)=Ccospy+Dsinpy

(33)

将矩形薄板两条竖直边界x=0，x=a代入到式(30)整理得H(0)=Acos0+Bsin0=0；H(a)=Acosak+Bsinak=0即Bsinak=0分两种情况讨论，当B=0时，函数H(x)没有意义，所以不成立。当sinak=0即ak=mπ，m∈N。

(34)

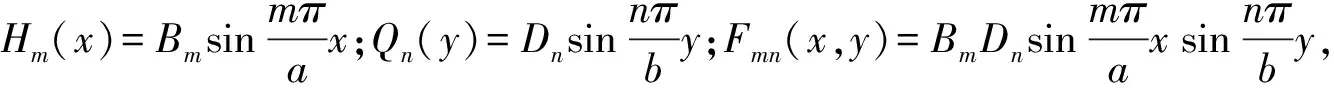
(35)

将式(35)进行归并整理成如式(36)所示。

(36)

将所有模态组合在一起，形成如式(37)所示。

(37)

起始条件u(x,y,t=0)=f(x,y)，将t=0代入到式(37)整理得如式(38)所示。

(38)

对式(38)运用傅里叶逆变换可得如式(39)所示。

(39)

将式(37)代入式(19)可得如式(40)所示。

(40)

对式(40)运用傅里叶逆转换可得如式(41)所示。

(41)

根据边界条件为齐次和初始条件为非齐次，运用分离变量法对矩形薄板固定边界波动问题进行分析研究，将波动方程为偏微分方程变量分离转化为含有单一变量的常微分方程并求解出该类问题解的形式，能够总结出分离变量法可以用来求解二维平面薄板的波动问题。

5 求解矩形薄板热传导问题

一个长为a，宽为b的矩形薄板如图5所示，上下两面绝热、四周边界温度已知。可以表示成：板的两边(x=0，x=a)始终保持零度，另外两边(y=0，y=a)的温度分别为f(x)和g(x)。

图5 矩形薄板热传导问题的二维平面图

矩形区域上拉普拉斯方程边值问题如(42)式所示。

(42)

令u(x,y)=X(x)Y(y)进行变量分离，方程式(42)可以进一步转化为如式(43)所示。

(43)

对式(43)中关于变量x和y进行移项整理得如式(44)所示和式(45)所示。

X″(x)+α2X(x)=0

(44)

Y″(y)-α2Y(y)=0

(45)

根据边界条件求解本征方程X(0)=0和X(a)=0的固有值如式(46)所示。

(46)

固有函数如式(47)所示。

(47)

式(46)代入如式(45)可得如式(48)所示。

(48)

式(48)中的解可以表示如式(49)所示。

(49)

原定解问题的解为如式(50)所示。

(50)

由边界条件得如式(51)所示。

(51)

应用傅里叶系数公式得如式(52)所示。

(52)

当矩形区域的两组对边的边界条件都是齐次时，方程只有零解，这从物理模型上分析也是显然的。若两组边界条件都是非齐次，则无法直接应用分离变量法。此时，可以根据叠加原理，将其分解为两个各含有一组对边是齐次边界条件的边值问题，再利用分离变量的方法分别求解。对于二维薄板热传导的拉普拉斯方程的边值问题而言，应根据求解区域的形状适当地选取坐标系，使得在此坐标系中边界条件的表达式最为简单，便于求解。只有当求解区域很规则时，才可以应用分离变量法求解拉普拉斯方程的边值问题。

矩形薄板在不同边界条件下对X″+α2X=0和Y″+β2Y=0的特征值与特征函数可以进行总结。垂直边界X=0，X=a在边界X″+α2X=0的特征值及特征函数可以总结如表3；水平边界Y=0，Y=b在边界Y″+β2Y=0的特征值及特征函数可以总结如表4。

表3 垂直边界条件特征情况

表4 水平边界条件特征情况

6 结论

应用分离变量法求解平面薄板的四边自由振动模型、四边固定的波动模型、四边稳恒状态热传导模型，可以总结出一些结论。

(1)求解二维平面薄板定解问题时：当泛定方程与边界条件均为齐次时，无论初始条件为何种情况，可直接应用分离变量法求解。

(2)当边界条件为齐次，泛定方程或初始条件为非齐次时，泛定方程为齐次并具有原定解条件的定解问题则可以分离变量法求解；泛定方程为非齐次的并具有齐次定解条件的定解问题，该问题用固有函数法求解。

(3)当边界条件为非齐次时，则必须引进辅助函数把边界条件化为齐次的，然后再应用分离变量法来求解。