一种基于Fast ICA和K-Means++融合算法的雷达脉冲聚类方法

李 伟

(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)

0 引 言

由于电子对抗以及各种实际应用的需求越来越旺盛，雷达技术近些年获得了极大发展，信号环境也越来越复杂，各方面因素导致雷达接收机所能接收到信号的质量大大下降。传统的建立在容差上的雷达信号分选受参数变化的影响大，所以需要更能适应复杂信号环境的参数测量算法，但这往往是不容易的，而且在脉冲描述字(PDW)参数相近时传统方法几近失效，已经无法适应新环境[1-2]。

在实际进行雷达信号分选时分析发现，将盲源分离算法和聚类算法应用于雷达信号分选时两者有很强的互补特性，因此本文试图将ICA算法的改进方法Fast ICA[3]以及K-Means算法的改进方法K-Means++[4]分别优化后融合，设计一种高密度脉冲流环境下的未知雷达源实时分选方法，通过Amdahl加速比定律于CPU+GPU异构系统将其加速实现。

1 Fast ICA算法

Fast ICA算法一般有如图1所示流程，主要分为数据预处理、循环迭代和后处理三部分。

图1 FastI CA算法流程图

预处理部分主要完成数据的去冗余化过程，主要包括数据中心化和白化。数据经零均值化后可有效消除迭代时的zig-zag运动，并且可以得到协方差矩阵为单位阵的效果，可以有效减少主处理迭代次数，提升运算效率。数据白化具体为去除数据中的相关性，达到数据降维的目的，一种常见的白化方法是对数据的协方差进行奇异值分解(SVD)，假设经中心化后的矩阵为X，白化后的信号矩阵为C,C各分量之间不相关且有单位方差，其协方差矩阵满足E{CCT}=I,则上述基于SVD的白化方法可描述为：

E{CCT}=FDFT

(1)

式中：F为E{CCT}的特征向量组成的正交阵;D为E{CCT}的对角特征值矩阵，则白化矩阵W=D-1/2FT,白化后的信号C可表示为C=D-1/2FTX。

白化操作能有效减少迭代部分的待估参数，若X要估计n2个参数，则C只需要估计n(n-1)/2个，减少了ICA一半的工作量。

主处理部分为根据设定条件循环迭代求取分离矩阵。由于目标函数的选择直接决定着ICA的速度和质量，本文选择的基于负熵的Fast ICA算法的目标函数可表示为[3,5]:

J(B)={E{G(BTZ)}-E{G(V)}}2

(2)

式中：B为分离矩阵；E(·)为求均值运算；V为与BTZ协方差相同且为零均值的高斯随机向量；G(V)为非线性函数，本文选取G(V)=tanh(V)。

本算法估计独立成分是通过将式(3)所示目标函数最大化来实现，而G(B)的极大值在E{G(BTZ)}的极值点处取得。由拉格朗日条件，可在E{(BTZ)T}=‖B‖2=1的约束条件下，通过求解下式来获取E{G(BTZ)}的最优值：

E{Zg(BTZ)}+βB=0

(3)

据式(3)建立函数：

F(B)=E{Zg(BTZ)}+βB

(4)

利用牛顿迭代法对式(4)进行求解，得到近似牛顿迭代公式：

(5)

则由简化后的Fast ICA迭代公式：

(6)

可得分离矩阵B。

后处理则是利用得到的分离矩阵B并结合观测信号Xi求得近似的源信号Yi=BTXi。

以上Fast ICA算法可以概括为以下几个步骤：

第1步：将硬盘中的观测数据读入内存，CPU准备处理。

第2步：数据预处理，将读入的雷达脉冲数据做中心化和白化处理。

第3步：设定分离控制条件，对预处理后的数据进行循环迭代运算求解分离矩阵。

第4步：根据观测信号及分离矩阵求解估计的未知雷达源信号。

第5步：将数据由内存写入硬盘。

2 K-Means++算法

K-Means++算法由K-Means算法改进而来，只不过是初始聚类中心选取方法不同，先介绍K-Means算法的工作原理，具体如下：

第1步，想要把输入样本数据分为几类，就将K设置为几，然后在样本数据中随机选取K个初始点作为初始聚类中心;

第2步，求所有样本点到这K个初始点的距离，离哪个初始点近就将其归于哪一类;

第3步，对每一聚类好的簇重新计算聚类中心μi;

第4步：重复第2步和第3步直到μi的位置在给定误差内变化。

由于K-Means算法初始聚类中心选取时是随机的，因此每次聚类都可能出现不同的聚类结果，而且容易陷入局部最优聚类，而K-Means++就很好地解决了这个问题，选取初始点不都是随机的，而是根据不同聚类之间分得“越开越好”的原则，具体步骤如下：

第1步，在数据集中随机选取1个初始聚类中心c1；

第2步，计算数据集χ中每个样本x与已有最近聚类中心的距离D(x),再接着计算每个样本被选为下一聚类样本的概率:

(7)

并利用轮盘法确定下一聚类中心；

第3步，重复第2步直到确定出K个聚类中心；

之后的步骤同K-Means算法的第2～4步。

K-Means算法及其改进算法进行聚类时的相似度衡量都是基于样本之间的欧氏距离，样本大值的属性往往起着决定性作用，而样本的其他属性没有起到应有的作用，这可能导致大的聚类被分割，聚类结果错误。此问题在实际应用中经常遇到，可通过对所有维度上的信息都做归一化处理，即将所有脉冲描述字的参数值大小都映射到[0,1]区间来解决，当然还可根据某一参数的可信度适当增加其权值，使得分选更加准确，则得到K-Means++算法流程图如图2所示。

图2 K-Means++算法流程图

3 基于Fast ICA和K-means++的融合算法

通过分析发现，Fast ICA和K-means++2种算法能互补的特性主要有：

(1) Fast ICA能够准确提取出未知雷达源的个数，为K-means++提供聚类所需的K值；

(2) Fast ICA能够分离出噪声进而排除噪声的影响；

(3) K-means++简单，易于实现，有很好的并行化实现基础，能有效解决Fast ICA分选速度慢的缺点；

(4) K-means++基于脉冲描述字(PDW)，可根据其中比较稳定的脉冲到达角度(DOA)参数对Fast ICA要处理的雷达脉冲进行分块，降低雷达脉冲流密度。

基于以上的融合基础，下面给出融合思路：

第1步，考虑雷达辐射源的位置不会突变，利用PDW中的DOA参数对接收到的脉冲按每15°进行空间划分，分块存储，达到稀释雷达脉冲流的目的，为接下来的数据处理做准备。

第2步，从上一步按到达角度划分的数据块中随机抽取部分雷达脉冲信号，利用Fast ICA算法对其进行独立成分分析，分离出雷达信号和随机噪声以及雷达信号种类K。

第3步，根据上一步得到的雷达信号种类K,基于WPD={σPW,AP,fR}三参数对雷达脉冲进行快速聚类分选。

第4步，得到雷达信号分选结果，将其存储回硬盘以供后续处理。

进一步分析融合算法的每一步骤，根据数据量以及运算模式(是否涉及大量重复的低耦合运算)确定是否需要并行化实现。且尽量在GPU中做并行度高的数据计算工作，在CPU中做一些条件判断的工作。融合后的算法流程图如图3，Fast ICA中的数据中心化以及白化都可转化为简单矩阵运算，有成熟的于GPU中运行的并行矩阵运算API函数可供调用；K-Means++中的核心聚类迭代部分是一种非常理想的无耦合关系的计算模型，也于GPU中展开运算。

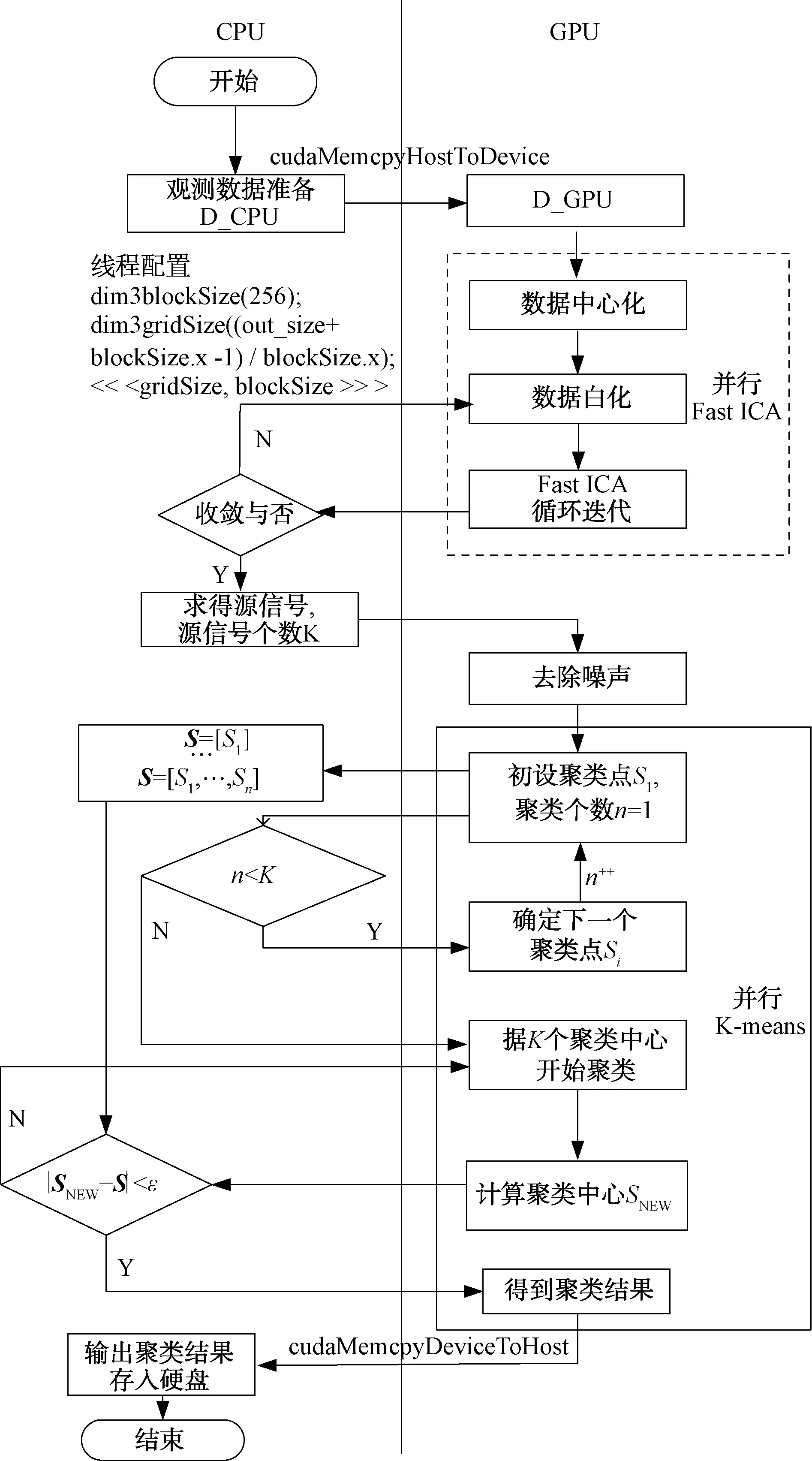
图3 并行的基于ICA的K-means++算法流程图

4 仿真实验及分析

用MATLAB仿真了线性调频雷达信号、二相编码雷达信号、方波雷达信号以及随机噪声信号，然后利用融合算法对其进行分选，仿真使用的雷达信号参数如表1所示：

表1 雷达辐射源参数

表1中2FSK体制雷达的编码为“11001”。按照本文提出的方法对表1中的信号进行预处理，原始信号、混合、解混的仿真结果如图4所示。

图4 融合算法Fast ICA阶段信号处理仿真结果

由图4可以看出，本文基于CPU+GPU的并行融合算法在Fast ICA预处理阶段成功分选出了雷达辐射源信号以及噪声信号，可以直观地得出有3部雷达辐射源以及1个噪声干扰，利用自相关累加的方法对分选出的信号进行处理，剔除噪声信号，然后将此次分选结果交由并行K-Means++主处理部分，对脉冲描述字信息进行快速实时聚类。在进行并行K-Means++主处理时，由于PA参数相差不大，因此采用WPD={σPW,fR,tPRI}三参数进行聚类，聚类个数K已由Fast ICA预处理部分得出，为3，最终可得其聚类结果为：

WPDcenter=[σPW,fR,tPRI]=

(8)

由式(9)同表1比较可得，该融合算法成功分选出了3部雷达辐射源信号，由于2FSK信号在80 MHz和60 MHz上跳变，此融合分选算法得出了其中间频率为70 MHz。

以上实验证明本文提出的基于Fast ICA和K-means++的融合算法对未知雷达信号具有较好的分选效果。

5 结束语

本文分别对Fast ICA和K-means++算法进行介绍，结合2种算法的特点提出了基于Fast ICA和K-means++的融合算法用于雷达脉冲聚类。该方法利用Fast ICA对接收到的雷达脉冲数字信号进行预分选，预分选步骤能有效分选出混叠信号中的独立成分，确定出独立成分的个数，去除噪声成分，保证了K-means++算法对提取的脉冲描述字信息分选的正确性。该方法在军事电子对抗领域具有一定的应用前景。