成层土中吸力锚极限承载力的数值模拟及分析

马鹏程， 邱 月， 舒 爽

（1.河海大学岩土力学与堤坝工程教育部重点实验室，南京 210098；2.山东科技大学矿山灾害预防控制-省部共建国家重点实验室培育基地，山东青岛 266590）

资源开发对于国家的工业发展越来越重要，在我国东部海域与南部海域储藏着大量的油气资源，海上平台作为开采油气资源的主要设备，更加准确、合理地评估其安全性与稳定性至关重要. 吸力锚作为一种方便快捷的基础形式被广泛应用于海洋工程，特别是海上风力发电机、海上平台等，其在服役期间的稳定性是保障上部结构正常运营的重要环节. 对于离岸海上浮式、半浮式平台、海上平台与吸力锚通过锚链连接，海洋环境恶劣，结构物长期受到受风、浪、水流等荷载作用，在复杂循环荷载条件下，吸力锚基础除了自重外，长期受到通过锚链传递而来的水平荷载、弯矩荷载. 我国海域海床多为软土，因此，分析基础在软土层中的承载特性是工程设计的基石.

在荷载作用下，若吸力锚只发生平动，则吸力锚发挥出最佳的承载能力，此时吸力锚与锚链的连接点为最优系泊点，最优系泊点所在水平面与吸力锚中心轴线的交点为最优加载点. 海床情况复杂，吸力锚的穿透深度内可能存在性质差异较大的软土层. Ahn等［1］使用ABAQUS研究了吸力锚在不同抗剪强度土中的最优加载点分布规律，Kellezi 和Stromann［2］利用大变形有限元模拟在软土覆盖硬土的情况下桩靴的灌入过程；Zhu等［3］利用循环加载设备探究在砂土、黏土和砂土覆盖黏土条件下吸力锚承载力变化规律；Zhao等［4］利用SNAME方法预测出桩靴在砂土覆盖黏土灌入过程中承载力变化的相关规律；张其一等［5］利用ABAQUS研究二维状态下不同长径比时吸力锚水平承载力规律；Jeanjean等［6］使用土工离心机得出了吸力锚在多层土上拔过程中外侧与内侧抗拔力规律；Supachawarote等［7］应用有限元软件分析了吸力锚水平、竖向以及倾斜的承载力，并且得到了不同长径比下的破坏包络曲线；Deng和Carter［8］采用剑桥本构模型，通过有限元软件AFENA对吸力锚的承载力和破坏机理进行了分析；王志云等［9］通过分析吸力锚竖向荷载与水平荷载联合作用，得出其承载力变化规律；武科［10］利用有限元软件ABAQUS系统分析了单个和组合桶形基础的承载力以及荷载包络曲线，并计算了不同加载点下吸力锚承载力规律；韩智臣等［11］基于总应力分析法，利用ABAQUS系统分析了不同高度系泊点处施加荷载后吸力锚的破坏模式，得到了最优系泊点上的倾斜承载力包络图；孙晓东等［12］通过模型试验观察并分析了单桩与群桩在成层土内贯入过程中桩周土体的位移变化情况. 众多研究探究了成层土中承载特性以及单一土层的最优系泊点变化，尚缺乏吸力锚在成层土中的承载力特性、周围土体变形情况和最优加载点位置相关规律. 郑刚和王丽［13］采用有限元软件ABAQUS 系统研究了成层土条件下单桩受倾斜荷载作用时各土层内桩的受力情况；刘振纹［14］利用有限元软件分析并推导出吸力锚在水平荷载作用下，土体抗力仅分布在桶体前侧时水平承载力的计算公式；陈强华和陈冠发［15］通过现场实验研究了成层土中不同贯入深度单桩水平荷载作用下的位移变化规律；Rao等［16］通过SOCP与有限元对双层黏土上的刚性条形基础在倾斜与偏心荷载作用下的承载力进行了计算；刘金龙等［17］运用大型有限元软件Plaxis 3D分析了水平荷载作用下系泊点的位置对吸力锚承载力及旋转姿态的影响；Farhan等［18］利用室内实验探究了成层土中不同长细比单桩以及不同土层厚度对桩承载力的影响.

在此基础上，本研究使用有限元软件ABAQUS进行数值模拟，系统分析了成层土条件下吸力锚的水平、竖向承载特性并绘制V-H破坏包络线，同时探究了成层土中吸力锚最优加载点位置的变化规律，提出的经验公式能够为实际工程中提供指导建议.

1 有限元模型

1.1 几何尺寸及网格划分

为了研究软土覆盖硬土条件下吸力锚最优加载点的位置以及刻画竖直-水平（V-H）荷载下的破坏包络线，使用有限元软件ABAQUS 建立模型进行数值模拟分析. 考虑到吸力锚与土体的几何结构以及荷载作用结果具有对称性，选取吸力锚与周围土体的一半建立有限元模型，以提高计算效率. 吸力锚外径D=5 m，长度L=10 m，锚壁厚度t=0.05 m. 为消除边界效应影响，土体模型竖向高度取3L，直径取15D. 吸力锚模型二维简化示意图如图1所示. 其中，D为吸力锚直径，L为吸力锚长度，θ为位移施加角度，Zp为最优加载点与土体表面距离，W为模型宽度，H为模型高度，t为锚壁厚度，h为软土层厚度.

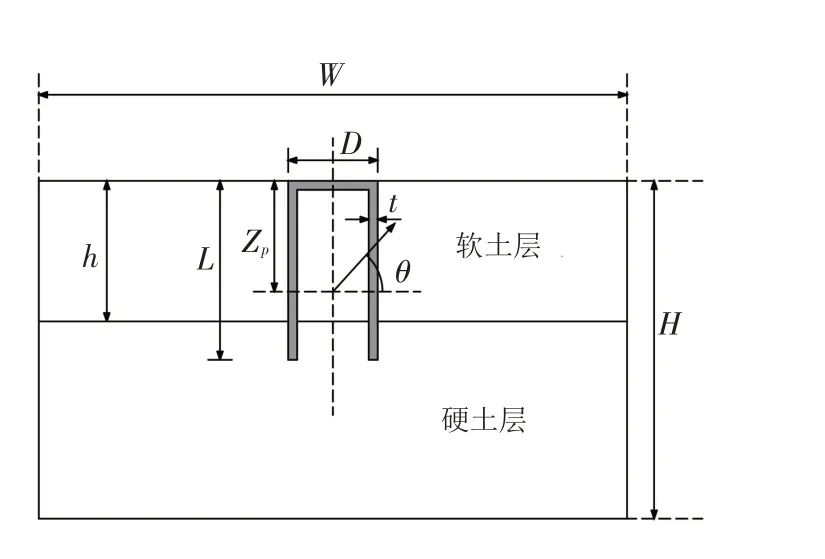
图1 吸力锚模型及参数Fig.1 Suction anchor model and parameters

为了提高计算精度同时兼顾计算效率，近锚处土体采用密网格，远离吸力锚的土体采用疏网格，吸力锚为刚性体，采用R3D4 单元，土体采用6 面体8 节点缩减单元（C3D8R）模拟. 有限元网格划分与坐标轴朝向如图2所示.

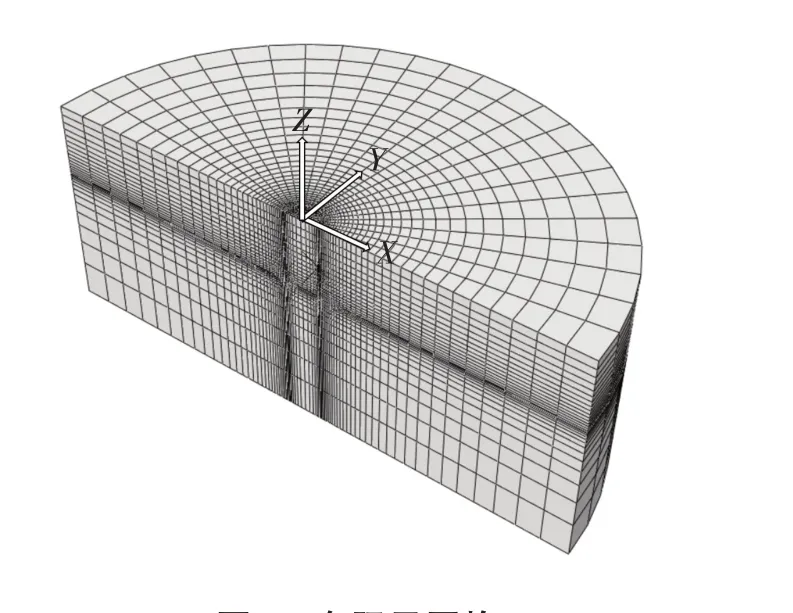
图2 有限元网格Fig.2 Finite element mesh

1.2 边界条件

由于吸力锚为刚性体，在锚顶圆心内侧位置设置参考点，并限制参考点X、Z方向旋转自由度与Y方向位移自由度，保证吸力锚只能在X轴与Z轴所在平面内平动与旋转. 土体底部限制三个方向的位移自由度，竖向边界限制X方向位移自由度与Y方向位移自由度. 认为底部边界无任何位移，侧向边界无水平位移.

1.3 材料与接触属性

吸力锚周围土体为无重度黏土，整个土体上层为软土层，下层为硬土层. 根据Zhang等［19］的参数选择，软土层内摩擦角和黏聚力分别为φ=0°，cu=11 kPa，弹性模量和泊松比分别取E=500cu=5.5 MPa，v=0.49；硬土层内摩擦角和黏聚力分别为φ=0°，cu=38.3 kPa，弹性模量和泊松比分别取E=500cu=19.15 MPa，v=0.49.土体均服从Tresca 强度屈服准则，并满足相关联流动法则. 吸力锚设置为不可变形刚体，与土体单元采用“tie”接触方式，假定吸力锚与土体紧密连接.

2 加载方式

分析采用位移加载方式，位移施加在吸力锚参考点处.如图3所示，将合位移分解为水平位移和竖向位移，在荷载施加分析步中同时施加对应的水平位移与竖向位移.

图3 参考点及加载方式Fig.3 Reference point and loading pattern

在位移控制下，施加位移的方向由水平位移分量和垂直位移分量的大小和方向决定. 位移逐渐增加，直至反作用力不再增加，即恒定荷载下的持续变形. 如果没有达到持续变形，以0.2D位移处的荷载值为极限承载力［20］.

为了探究分层土中不同软土层厚度对吸力锚承载力的影响，以0.1L为梯度，计算h=0L至h=2.0L时分别施加θ=0°、θ=10°、θ=15°、θ=30°、θ=45°、θ=60°、θ=75°、θ=90°方向位移后吸力锚荷载变化情况.

3 分析结果

3.1 极限承载力

水平位移作用下，吸力锚沿着加载方向发生向前的倾覆转动，筒体逐渐倾斜，周围土体在荷载作用下发生变形.图4给出了吸力锚水平荷载随位移的变化曲线. 当位移从0 m增加值0.05 m时，水平荷载位移曲线处于弹性阶段，位移与荷载的关系呈线性变化；0.05 m至0.1 m阶段，曲线斜率骤变，由高度倾斜逐渐平缓，此时吸力锚发生破坏；0.1 m之后曲线斜率基本不变，吸力锚持续变形. 当位移达到0.2 m之后水平承载力增加趋势迅速减小并趋于收敛，证明了本文选取位移达到1 m（即0.2D）时对应的承载力作为极限承载力是合理的. 随着软土层逐渐变厚，吸力锚所处地基中软弱土占据越来越高的比例，周围土体承载力逐渐变弱，因此吸力锚水平位移荷载曲线的弹性阶段、弹塑性阶段与塑性屈服阶段均呈现下降的趋势. 位移加载过程中，吸力锚四周土体受扰动最大，锚底以下的土体扰动小，因此当h＞1L后，水平位移荷载曲线重合，证明影响吸力锚水平荷载位移曲线的主要是吸力锚底部上方土层的抗剪强度.

图4 水平荷载随位移的变化曲线Fig.4 Relationship of horizonxal loads-displacements

图5 给出了水平荷载作用下吸力锚破坏机制. 锚周围土体自顶向下变形量逐渐减小，由主动区过渡到被动区，对承载力的贡献量也随之减少，因此，每当0.1L厚度的硬土层被软土层替代，该0.1L厚度软土层相对于硬土层的承载力减小值会随深度的增加而逐渐变少.图6表明，吸力锚水平极限承载力随软弱土层厚度的增加逐渐降低，软土层厚度h=0L时，吸力锚的水平极限承载力达到最大值，最大值为4 097.75 kN，软土层厚度增加至h=0.1L时，吸力锚水平极限承载力减小535.77 kN，减小幅度最大，随着软土层厚度的增加，水平极限承载力的减小幅度逐渐缩小，并于h＞1.0L后稳定在1177 kN，证明锚底下方土体的抗剪强度几乎不会影响吸力锚水平极限承载力. 这与吸力锚的破坏机制有关，吸力锚破坏时更多是四周土体出现屈服，底部扰动区域小，因此对承载力的影响也小.

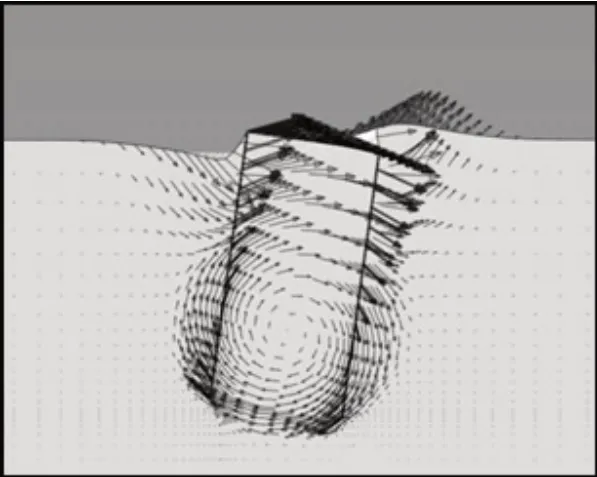
图5 水平荷载作用下吸力锚破坏机制Fig.5 Failure mechanism of suction caisson under horizontal loads

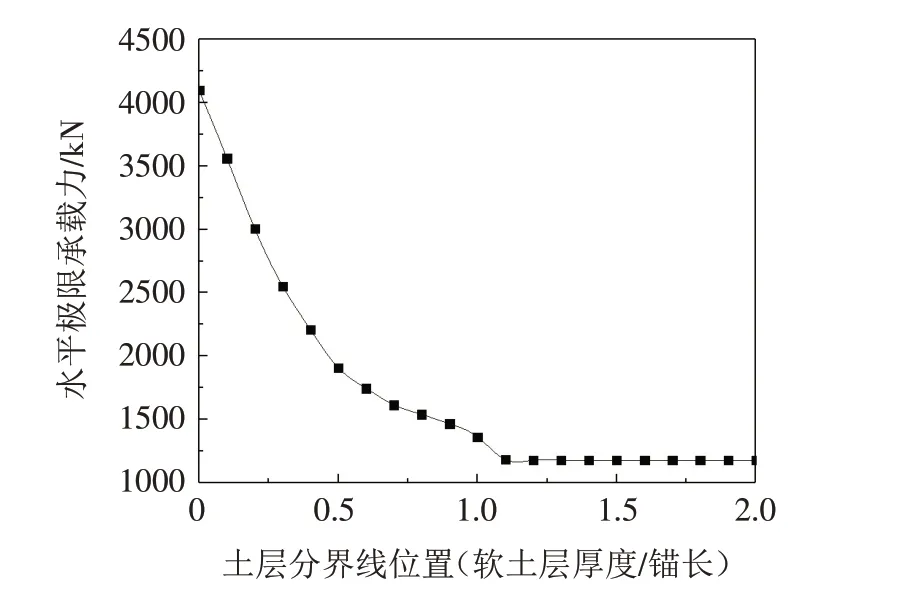
图6 土层分界线位置对水平极限承载力的影响Fig.6 Effects of the heights of boundary between soil layers on the horizontal bearing capacities

仅施加竖向荷载时，吸力锚向上平动，锚壁外侧土体出现剪切破坏，锚内部土体带动下方土体上移，两侧土体向锚底流动. 图7给出了吸力锚竖向荷载随位移的变化曲线，软土层厚度的逐渐增加导致吸力锚承载能力降低，当软硬土层分界线降至锚底以下（即h＞1.0L），随着软土层厚度增加，吸力锚竖向荷载随位移变化曲线逐渐重合并保持一致. 图8 表明，软土层厚度增加导致土体竖向抗剪能力降低，土体极限承载力降低. 当h＜1.0L时，吸力锚的破坏主要表现在侧向土体屈服，锚内部土体在负压作用下与内壁紧密接触，竖向荷载作用下土塞带动下方硬土层同时移动，由于硬土强度较大，没有出现屈服. 当h＞1.0L时，吸力锚下方土体出现软土层，由于软土层抗剪强度低，在相同的位移加载条件下，软土因变形过大发生屈服，导致上拔过程中土塞底部受力减小，因此会出现h=1.0L与h=1.1L时吸力锚的竖向承载力相差较大的情况.

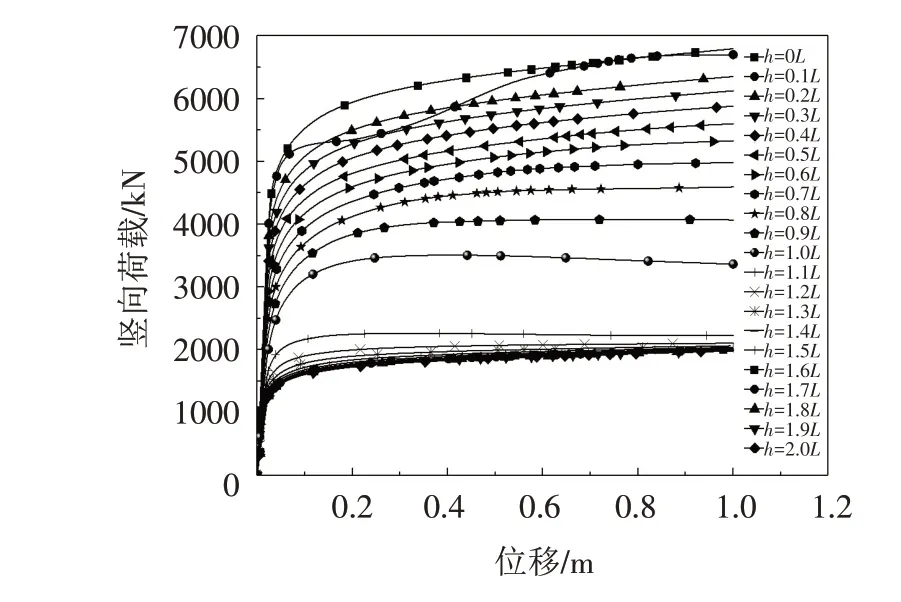
图7 竖向荷载随位移的变化曲线Fig.7 Relationship curves of vertical loads-displacements

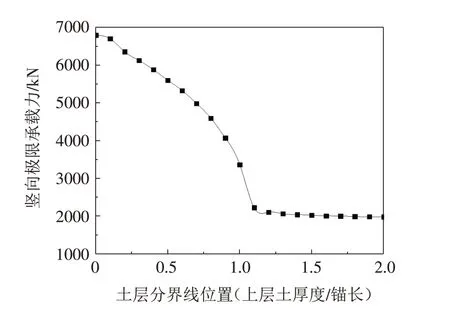
图8 土层分界线位置对竖向极限承载力的影响Fig.8 Effects of the heights of boundary between soil layers on the vertical bearing capacities

3.2 破坏包络线

图9 给出了吸力锚在不同软土层厚度下，VH 荷载组合下的极限承载力包络线，由图可知，随着软土层厚度增加，吸力锚的水平承载力和竖向承载力逐渐减小；h＞1.0L后破坏包络线趋于重合，这是由于吸力锚承载力影响区域主要是锚底以上土体，锚底下方土体的强度变化对吸力锚承载力的影响很小，从而导致当h＞1.0L后破坏包络线重合. 图10 为归一化荷载破坏包络线，其中，H为水平极限承载力，V为竖向极限承载力，Hult为最大水平极限承载力，Vult为最大竖向极限承载力. 从图中可以看出，在锚底上方土体分层的情况下，θ=10°对应的水平极限承载力大于θ=0°的水平极限承载力. 因此，在土体分层条件下，施加一定的竖向荷载可以提高吸力锚的水平极限承载力.

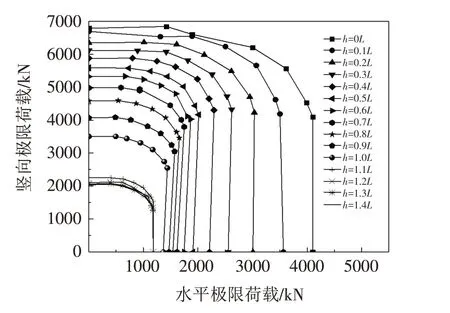
图9 V-H承载力破坏包络线Fig.9 V-H bearing capacity failure envelopes

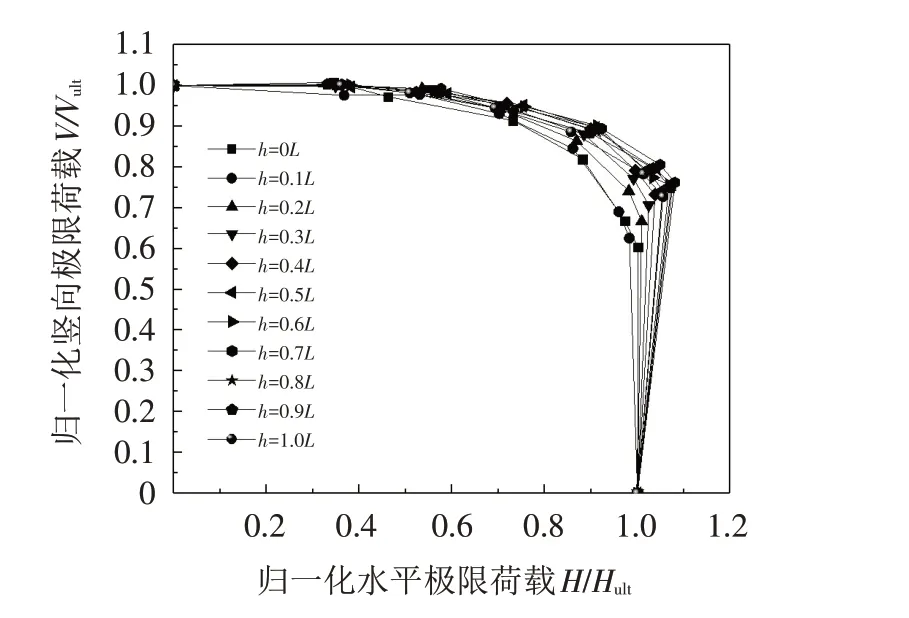
图10 归一化荷载破坏包络线Fig.10 Normalized V-H load failure envelopes

3.3 最优加载点

仅允许吸力锚沿x方向平动，限制其旋转自由度，通过弯矩平衡计算出吸力锚沿中心线的最优加载深度Zp. 施加的荷载可以从参考点移动至吸力锚中心线上距离锚某一深度处，如图11所示. 在这种情况下，最优加载点的位置即吸力锚参考点处的反力矩除以水平荷载［20］. 其中，H为水平荷载，V为竖向荷载，Zp为最优加载点与土体表面的距离，M为施加的弯矩，O点为最优加载点.

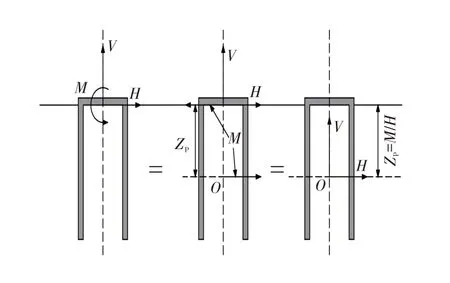
图11 最优加载点位置计算Fig.11 Calculation of the heights of the optimal loading points

软土层变厚过程中，由于软土层抗剪强度低，相同变形量条件下硬土层会承受更多的荷载，最优加载点位置下移；h＞0.7L后，软土层开始承受更多的荷载，最优加载点上移. 吸力锚平移过程中主要是锚壁侧向土体承受挤压力，当h＞1.1L后，最优加载点位置不再变化. 图12给出了吸力锚最优加载点位置随土层高度分布. 随着软土层厚度逐渐增加，吸力锚最优加载点与吸力锚顶盖的相对距离先增大后减小，当土层分界线下降至锚底以下，吸力锚的最优加载点保持不变，证明锚底下方土体的抗剪强度不会影响吸力锚最优加载点的位置. 为了更好地反映成层土条件下吸力锚最优加载点的变化规律，利用多项式函数对0＜h/L＜1.1段曲线进行拟合，用来描述h/L与Zp/L之间的关系. 拟合曲线方程如下：

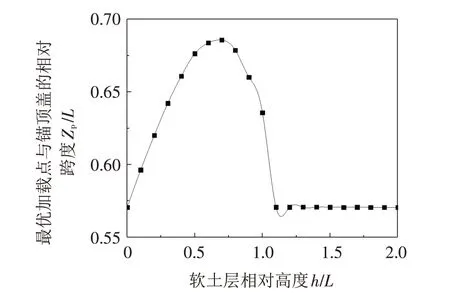
图12 最优加载点分布Fig.12 Distribution of optimal loading points

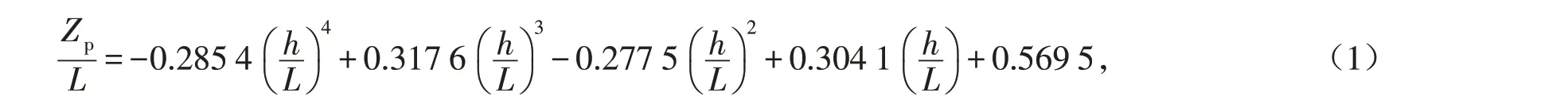
式中：Zp为最优加载点到吸力锚顶盖的距离；L为吸力锚长度；h为软土层厚度.

4 结论

本文通过三维有限元数值模拟计算，探究了成层土条件下吸力锚水平竖向联合承载力规律，以及最优加载点位置变化规律，分析了软土层厚度对吸力锚承载力和最优加载点位置的影响，得到以下结论：

1）软土层厚度对吸力锚各方向的承载力影响较大，当软土层厚度逐渐增加时，吸力锚V-H 联合承载力包络线缩小，吸力锚水平极限承载力与竖向极限承载力逐渐减小，这与软土层抗剪强度弱于硬土层有关.

2）吸力锚水平极限承载力随软土层厚度的增加逐渐降低，并于h＞1.0L后保持不变；h=1.0L与h=1.1L处施加竖向荷载时，由于二者的屈服模式不同，竖向极限承载力发生突变.

3）随着软土层厚度的增加，吸力锚最优加载点到吸力锚顶盖的相对距离先增大后减小，并于h＞1.0L后保持不变.h=0.7L时达到最大值. 本文建议的最优加载点公式可以很好地反映成层土工况下的最优加载点位置.