采石场爆破粉尘运移规律的数值模拟

李 勃， 董小琴

（1.湖北省电力勘测设计院有限公司，武汉 430000； 2.湖北工业大学土木建筑与环境学院，武汉 430000）

随着国内建筑业和基础设施建设的快速发展，社会对混凝土的使用量快速增长，需要开发大量采石场以开采混凝土所需骨料［1-2］. 在采石场骨料资源开采过程中，爆破作业是必不可少的工艺环节［3］，爆破过程中产生的大量烟尘，不仅会污染环境，还会给安全生产和现场作业人员的身体健康带来极大的威胁［4-7］. 研究采石场爆破粉尘颗粒的运移和扩散规律对粉尘防治工作具有重要意义，可为制定防尘、降尘措施提供科学依据.

国内外学者对粉尘运移及扩散规律的研究颇多且研究方法多样，既有数值模拟和实验分析的方法，也有采用现场试验的方法. 蒋仲安等［8］采用ANSYS软件对卸矿站粉尘浓度进行数值模拟，模拟结果与实测结果基本吻合. 冯博等［9］基于离散相模型探究了综采工作面粉尘逸散规律，发现在不同区域的采煤机具有相似的粉尘扩散规律. 谭聪等［10］通过建立离散相模型对不同粉尘的含水率和风速条件进行了模拟，结果表明最佳控尘风速为1.5 m/s. 李雨成等［11］对金川龙首矿长距离掘进巷道进行定点监测发现，粉尘颗粒比例随粒径增大而减小. 目前对于爆破粉尘的研究主要集中在爆破炮烟分布规律、粉尘排放量等方面. 张云鹏和孔令华［12］研究了爆破炮烟的运移规律. 陶子夜等［13］建立了爆破拆除工程粉尘扩散模型. 王嘉莹等［14］根据爆破粉尘的亲水性和疏水性进行粉尘分离，确定了影响粉尘湿润性的主要因素为粉尘真密度和粒径. 刘坚等［15］运用粉尘扩散理论进行现场试验发现，粉尘排放量随着炸药用量的增加而增加，同时采用现场数据验证了水封爆破技术对降尘的重要作用. 针对采场的研究，廖贤鑫等［16］通过对某铁矿爆破烟尘源进行特征分析得出，爆破粉尘运移规律受到风流流场的显著影响；陈举师等［17］针对采场爆破作业粉尘过多且不易排出的现象，建议安装局部通风设施，且指出联络巷通风排尘的最佳风速为2 m/s. 针对粉尘运移的研究，研究成果主要集中在巷道型作业面、煤矿采场综采、综放工作面粉尘浓度分布规律等方面，针对采石场梯段深孔爆破粉尘的研究很少. 鉴于此，本研究以杨房沟采石场为研究对象，建立了三维几何模型，并通过对数学模型的求解研究了料场粉尘的运移规律，最后对模拟结果进行了可视化处理.

1 数学模型

基于气固两相流理论，模拟粉尘颗粒在风流作用下运移规律的数值计算方法主要有欧拉-欧拉法和欧拉-拉格朗日两种方法. 本研究采用欧拉-拉格朗日方法设置的离散相模型，将空气视为背景流体，将爆破粉尘颗粒视为离散流体，对采石场中爆破粉尘进行数值模拟研究，分析其在风流作用下的运移规律. 假定空气为不可压缩流体，分别建立连续方程和动量守恒方程：

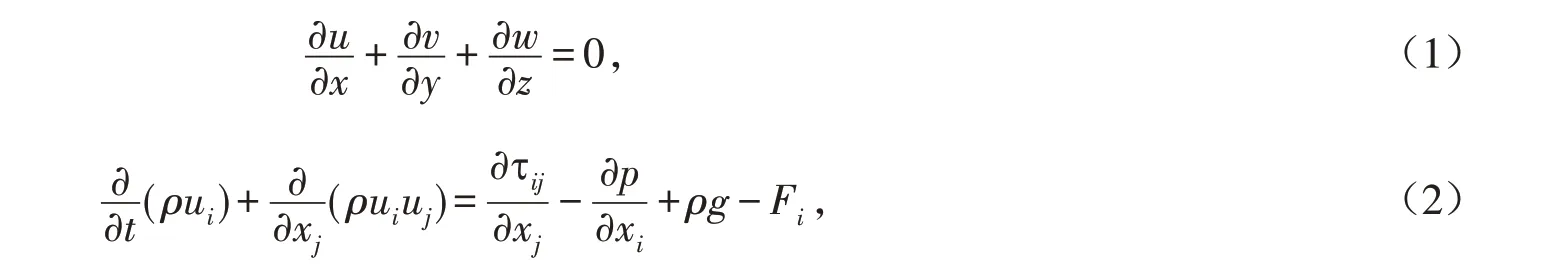
式中：u、v、w分别表示速度矢量在x、y、z方向上的分量，m/s；ρ表示密度，kg/m3；t表示时间，s；ui、uj分别表示x、y方向上的速度，m/s；xi、xj分别表示x、y方向上的坐标，m；τij表示应力张量；p表示压力，Pa；g表示重力，N；Fi表示控制体平均颗粒流体阻力，N.

根据标准k-ε湍流模型，颗粒的输运方程如式（3）和式（4）所示.

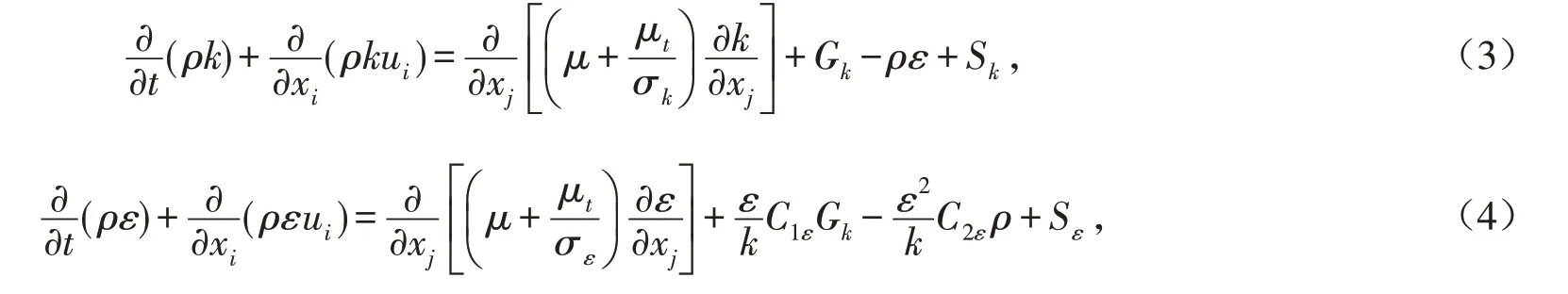
式中：k为湍流动能，J；Gk为湍流动能k的产生项；μ和μt分别为层流和湍流黏性系数，Pa·s；ε为湍流动能耗散率，m2/s3；Sk为湍流动能源项；Sε为湍流动能耗散率源项；C1ε、C2ε为经验常数，分别取值1.44、1.92.

在笛卡尔坐标系下，粉尘颗粒作用力平衡方程为如式（5）所示.

式中：FD(uf-up)表示颗粒单位质量曳力，N；ρp、ρ分别表示颗粒密度和流体密度，kg/m3；up、uf分别表示颗粒速度和流体速度，m/s.FD计算方法见式（6）.

式中：CD为曳力系数；dp为颗粒直径，m.

本研究采用随机轨道模型，故颗粒轨道控制方程为：

式中：ua为气流瞬时速度，m/s；τp为颗粒松弛时间，s.

2 三维模型的建立

2.1 现场概况

杨房沟采石场位于山体斜坡左侧，山体为35°～45°的斜坡地形；地表多基岩裸露，以坚硬的弱风化岩为主，内部岩性为花岗闪长岩，有用层储量为1 782.18 万m3；骨料物理力学性质良好，满足人工骨料原岩质量要求. 图1 为杨房沟采石场附近气象站点每月多年平均风速.

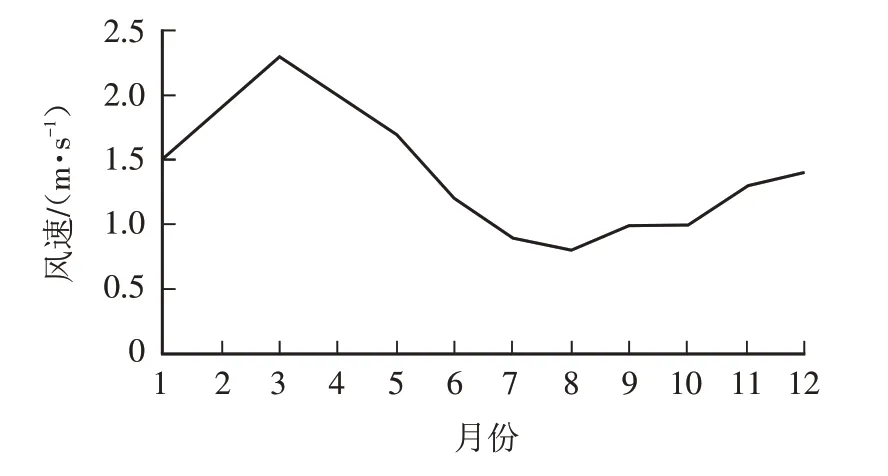
图1 采石场附近气象站点每月多年平均风速Fig.1 Monthly multi-year average wind speed at meteorological stations near the quarry

2.2 三维模型的建立

杨房沟采石场现场情况较为复杂，几何模型建立过程中难以遵照所有现场情况，需要根据该采石场现场实际情况和实测数据对模型及其计算区间做一定简化和假设，具体如下：①采石场边坡倾斜角度严格按照设计图纸开挖；②为保证现场人员安全，维护边坡稳定，边坡采用梯级台阶方式开挖，所有台阶宽度和高度均相等；③爆破面为平整水平爆破面；④料场外侧山体表面为平整坡面. 基于上述简化和假设，对该采石场进行几何模型的建立，如图2所示.

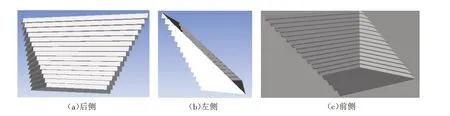
图2 采石场几何模型Fig.2 Geometry model of the quarry

根据模拟需要构建模型计算域，并利用Mesh软件对采石场和计算域进行网格划分，筛选网格质量和数量. 完成网格划分后，将三维模型导入FLUENT软件中进行模拟参数设定和数值模拟（图3）.

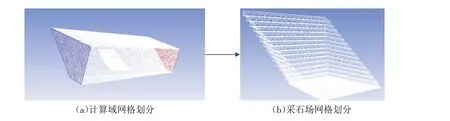
图3 计算域及采石场网格划分Fig.3 Computational domain and grid division of quarry

2.3 参数设定

本研究采用离散相模型对采石场爆破粉尘颗粒进行仿真分析，采用压力基求解器，运用SIMPLE压力速度耦合算法和标准k-ε湍流模型求解连续相流场. 结合采石场爆破实际情况创建离散相喷射源，设置材质、密度. 根据炸药用量与颗粒初始速度之间的函数关系，确定爆破颗粒初始速度为7 m/s. 通过爆破现场粉尘颗粒粒径分布测量结果得知，粒径分布符合Rosin-Rammler分布，且最小颗粒粒径为1×10-6m，最大颗粒粒径为1.16×10-4m，由此设置粒径分布及质量流率等参数. 爆破粉尘颗粒在风流作用下的速度等参数随时间而变化，故时间设定选择非稳态；入口边界类型和出口边界类型分别为速度入口、自由出流，其他数值模拟参数设定见表1.

表1 计算模型参数Tab.1 The calculation model parameters

3 爆破粉尘运移规律的数值模拟分析

3.1 不同视角下爆破粉尘颗粒的运移轨迹

为研究采石场中爆破粉尘颗粒的运移规律，在离散相模型中进行尘源设置，爆破面为粉尘颗粒的喷射面. 分别从采石场正视图和俯视图视角下，截取爆破发生后0、10、100、200、300 s 时粉尘颗粒速度分布图，研究粉尘颗粒速度大小在垂直方向和水平方向的分布情况，进而探究采石场爆破后粉尘颗粒的运移规律.

从图4可以看出，0 s时，采石场爆破工作还未进行，未产生爆破粉尘，其正视图和俯视图中均未出现粉尘颗粒.

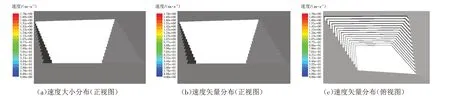
图4 采石场爆破粉尘颗粒速度大小及速度矢量分布情况（0 s）Fig.4 Velocity magnitude and velocity vector distribution of blasting dust particles in quarry（0 s）

由图5a可知，爆破发生10 s后，由于爆破发生时间较短，粉尘颗粒在爆炸冲击波的作用下从爆破面喷射而出，向上运移距离较短，粉尘颗粒未在采石场内大面积扩散. 在重力和空气阻力作用下，距离爆破面较远的粉尘颗粒速度较小，少部分较大粒径的粉尘颗粒速度趋近于0 m/s；距离爆破面较近的粉尘颗粒速度偏大. 图5b 为爆破发生10 s 后采石场正视视角下的粉尘颗粒速度矢量分布图，从中可以看到，受风流影响，采石场北侧（图中左侧）粉尘颗粒运移方向较为复杂，而南侧（图中右侧）粉尘颗粒大都趋向于向南侧运移.图5c为爆破发生10 s后采石场俯视视角下的粉尘颗粒速度矢量分布图，由图可知，采石场外侧粉尘颗粒在风流作用下被直接带走，颗粒速度趋近于风速；采石场内侧有三处速度较小，分别位于采石场北侧、南侧内部和中前侧.

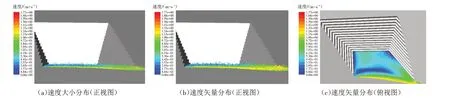
图5 采石场爆破粉尘颗粒速度大小及速度矢量分布情况（10 s）Fig.5 Velocity magnitude and velocity vector distribution of blasting dust particles in quarry（10 s）

图6展示了采石场爆破发生100 s后粉尘颗粒的运移情况. 由图6a可知，相较于爆破发生10 s后的运移情况，粉尘颗粒在垂直方向上的速度大小分布较为均匀，分层不明显. 从图6b可以看出，速度较大的粉尘颗粒均受风流流场的影响显著，运移方向较为统一，均朝向采石场南侧. 从图6c可以看出，采石场北侧粉尘颗粒速度较小，出现粉尘颗粒聚集现象. 整体来看，离开采石场的粉尘颗粒速度比采石场内部的粉尘颗粒速度大.

图6 采石场爆破粉尘颗粒速度大小及速度矢量分布情况（100 s）Fig.6 Velocity magnitude and velocity vector distribution of blasting dust particles in quarry（100 s）

从图7可以看出，爆破发生200 s后，部分粉尘颗粒在重力和空气阻力作用下发生自然沉淀，被地面及采石场三面台阶边坡吸附，部分粒径较小的粉尘颗粒由于重力较小，所以继续向上方及四周运移，此时粉尘颗粒已运移至采石场垂直方向上一半以上区域. 图7a显示，采石场内部大多为速度较小的粉尘颗粒. 由图7b可以得出，爆破发生200 s后，速度较大的粉尘颗粒依然是受风流影响较大的粉尘颗粒，其运移方向与风流方向紧密相关. 在风流流场作用下仍停留在采石场内部的粉尘颗粒速度均偏小. 图7c反映了粉尘颗粒的水平运移情况，此时，较小粒径的粉尘颗粒布满整个采石场区域，仍存在北侧粉尘颗粒聚集现象.

图7 采石场爆破粉尘颗粒速度大小及速度矢量分布情况（200 s）Fig.7 Velocity magnitude and velocity vector distribution of blasting dust particles in quarry（200 s）

图8为采石场爆破发生300 s后粉尘颗粒的运移情况. 从图中可以看出，相较于之前的粉尘颗粒分布情况，在风流的夹带作用、颗粒自身重力及空气阻力的共同作用下，采石场内部粉尘颗粒数量明显减少. 停留在采石场内部的粉尘颗粒粒径较小，受自身重力影响较小，由于风流流场作用，这些粉尘颗粒受风流影响不显著.

图8 采石场爆破粉尘颗粒速度大小及速度矢量分布情况（300 s）Fig.8 Velocity magnitude and velocity vector distribution of blasting dust particles in quarry（300 s）

3.2 不同高度下爆破粉尘的质量浓度分布情况

在采石场现场作业中，有工人（呼吸带高度约为1.5 m）、挖掘机及运输卡车司机（呼吸带高度约为2 m）等进行石料的开采和运输，因此研究不同高度下粉尘的质量浓度分布规律，可为制定更加有效的降尘措施提供科学依据. 本研究利用FLUENT后处理软件TECPLOT，分别对z=0 m（喷射面）、z=1.5 m（工人呼吸带高度）和z=2.0 m（挖掘机及运输卡车司机呼吸带高度）的粉尘质量浓度云图进行对比分析，以研究其分布规律.

图9分别展示了采石场爆破发生后1、50、100、300 s时在z=0 m、z=1.5 m和z=2.0 m高度下的粉尘质量浓度.

从图9可以看出，爆破发生1 s后，粉尘在爆炸冲击波作用下从喷射面上的爆破孔喷出，喷射面上粉尘颗粒密布，但此时爆破刚发生，垂直方向上的粉尘颗粒运移距离很短，故相较于喷射面z=0 m，在z=1.5 m平面上的粉尘颗粒较少，在z=2.0 m 平面上几乎没有粉尘颗粒出现. 爆破发生50 s 后，由于风流流场作用，粉尘颗粒在采石场北侧发生聚集现象，并在中部位置形成一条高质量浓度分布带，最高处的粉尘质量浓度达到4.8×10-3kg/m3，但从z=0 m到z=2.0 m的平面上，由于粉尘颗粒粒径不同引起的自身重力差异，不同粉尘颗粒的受力大小不同，故随着与喷射面的距离越来越远，粉尘质量浓度整体上出现逐渐下降的现象. 爆破发生后50 s到100 s时段内，在自身重力影响下，部分粉尘颗粒发生自然沉降，部分粉尘颗粒在风流的夹带作用下逐渐向其他方向运移，所以高质量浓度分布带上的粉尘质量浓度逐渐下降，但此时，采石场北侧出现粉尘颗粒聚集的现象，故其粉尘质量浓度相对较高. 爆破发生100 s后，采石场北侧越靠近喷射面，粉尘质量浓度越高.爆破发生300 s后，高质量浓度分布带已完全消失，粒径较小的粉尘颗粒较为均匀地分布在喷射面、现场工人呼吸带高度、挖掘机及运输卡车司机呼吸带高度上，在z=1.5 m高度上的粉尘质量浓度约为6×10-5kg/m3.

4 结论

基于气固两相流理论，采用流体力学软件FLUENT，建立了离散相模型，并对杨房沟采石场爆破粉尘的运移规律进行数值模拟，同时采用TECPLOT软件对模拟结果进行可视化处理分析. 得出主要结论如下：

1）爆破发生后，在风流的夹带作用下，采石场外侧的爆破粉尘颗粒沿着风流方向运移，被风流带出采石场，离开采石场后，粉尘颗粒运移速度趋近于风速.

2）由于受风流流场的显著影响，采石场内部的爆破粉尘颗粒速度较小，在采石场北侧出现粉尘颗粒聚集现象，粉尘质量浓度较高，并在采石场中部位置形成一条高质量浓度分布带. 部分粉尘颗粒因自身重力和空气阻力的影响发生自然沉降，部分粉尘颗粒在风流持续作用下沿着风流方向运移，在爆破发生50 s后高质量浓度分布带上的粉尘质量浓度逐渐下降，爆破发生300 s后，高质量浓度分布带已完全消失.

3）爆破发生后300 s内，采石场内不同高度的粉尘质量浓度分布存在差异. 爆破发生1 s后，z=0 m的喷射面上粉尘的质量浓度较大，而z=2 m的平面上几乎没有粉尘颗粒出现；爆破发生50 s后，z=0 m的喷射面上形成一条高质量浓度分布带，而z=2 m的平面上的粉尘颗粒分布规律与z=0 m和z=1.5 m平面上的不相同，且粉尘质量浓度偏低. 爆破发生300 s后，停留在采石场内的粉尘颗粒粒径较小，不同高度上的粉尘质量浓度差异也较小，粉尘颗粒分布较为均匀.