基于LMD和LSTM的盆式绝缘子典型缺陷局部放电模式识别方法

郭建鑫，赵玉顺，王志宇，丁立健

(合肥工业大学电气与自动化工程学院，合肥 230009)

0 引言

气体绝缘组合电器(gas insulated switchgear，GIS)具有占地面积小、运行稳定性高等诸多优点，被广泛应用于各电压等级的变电站中[1-2]，其绝缘可靠性直接影响电力系统的安全稳定运行。盆式绝缘子是GIS的核心绝缘部件，受生产制造、安装、运行过程中众多因素的影响，其表面和内部可能存在多种绝缘缺陷，因此在运行中容易发生局部放电，加速盆式绝缘子的绝缘损坏过程[3]。不同缺陷的局部放电带有不同的故障信息，通过分析可以对不同类型的局部放电信号进行分类[4-5]。但目前对于盆式绝缘子局部放电识别的研究较少，这为检修排障工作带来了困难，因此有必要针对盆式绝缘子典型缺陷局部放电的分类识别开展研究。

针对局部放电的分类识别，近年来国内外学者在特征量提取方法和分类器优化选择两方面开展了大量的研究，得到了较好的识别效果[6-8]。文献[6]将S变换与谱峭度算法结合，提取出包含局放信号主要信息的时频矩阵，并使用概率神经网络实现了分类识别。文献[7]提取了局部放电信号的26个统计特征参量并进行降维，通过多分类相关向量机进行分类识别。文献[8]利用在线序列极限学习机对局放信号的27个统计特征参量进行训练，得到了较高的识别正确率。上述文献大都先提取局部放电信号的特征矩阵或多个特征值，再对提取的特征进行识别，不同特征参数和特征矩阵的选取对分类结果影响较大，一定程度上削弱了上述方法的鲁棒性能。

长短期记忆神经网络(long short-term memory，LSTM)是一种改进的循环神经网络，能够解决时间序列中的长期依赖问题，在时序信号分类方面有出色的表现[9-10]。但局部放电信号包含的信息复杂，且信号点繁多，无法直接使用LSTM进行分类，因此关于LSTM在局部放电信号识别中应用的研究相对较少。为了解决该问题，本文引入局部均值分解(local mean decomposition, LMD)的方法，LMD是一种较新的自适应分解方法，它能够自适应地将信号分解为若干个位于不同频带的分量[11-12]，通过分割分量并提取其特征，形成满足LSTM训练要求的特征矩阵，实现局部放电信号的分类。

本文提出一种基于LMD和LSTM的盆式绝缘子局部放电识别方法。首先在实验室中制作了带有裂纹、气泡、嵌件毛刺、表面金属颗粒的缺陷样品并建立了盆式绝缘子局部放电实验平台，通过实验采集了大量信号，使用成对高斯白噪声辅助的LMD方法分解局部放电信号，再对分解得到的分量进行分割，提取每个片段的特征形成特征矩阵，输入LSTM中进行训练和分类识别，以验证所提方法的有效性。研究结果可为盆式绝缘子局部放电的特征提取与分类识别提供参考。

1 基于局部均值分解的局部放电特征提取

1.1 局部均值分解方法的基本原理

局部均值分解是Jonathan S. Smith最早提出的一种新的自适应非平稳信号的分析处理方法[13]。LMD方法能够自适应地将原始信号分解为若干个乘积函数(product function，PF)与1个残余分量之和。对于非平稳信号X(t)，其分解过程如下。

1)确定原信号X(t)的局部极值点，计算相邻两个极值点的平均值以及包络估计值。

(1)

式中：ni为原始信号X(t)的局部极值点；mi为相邻两个极值点的均值；ai为包络估计值。

使用移动平均法处理局部均值mi和包络估计值ai， 形成平滑变化的连续局部均值和包络估计值曲线，得到局部均值函数m11(t)和包络估计函数a11(t)。

2)从原信号X(t)中减去局部均值函数m11(t)， 再除以包络估计函数a11(t)对h11(t)解调。

(2)

3)将s11(t)作为原始数据重复步骤1)、2)中的迭代过程，即：

(3)

式中s1(n-1)(t)=h1(n-1)(t)/a1(n-1)(t)。

迭代是为了让a1n(t)的值尽可能接近1，但实际计算时无法让其无限迭代下去，因此迭代终止条件为a1n≈1。将迭代过程中产生的所有包络估计函数相乘便可以得到第1个PF分量P1(t)的包络信号a1(t)， 再将包络信号a1(t)与s1n(t)相乘得到第1个PF分量P1(t)。

(4)

式中q为循环迭代次数。

将P1(t)从信号X(t)中减去，得到1个新信号u1(t)， 将u1(t)作为原始数据重复步骤1)、2)、3)k次，如式(5)所示。

4)最终原信号X(t)将被分解为k个PF分量与残余分量uk(t)之和，如式(6)所示。

(5)

(6)

1.2 成对高斯白噪声辅助的自适应分解

模态混叠和端点效应是限制LMD应用的主要问题。本文使用成对高斯白噪声辅助分解的方法减轻模态混叠和端点效应[14-15]，具体方法如下。

1)向原信号X(t)中加入正负成对的高斯白噪声。

(7)

式中：ωi(t)为第i次加入的高斯白噪声信号；ε为高斯白噪声的幅值。

(8)

3)循环步骤1)和2)N次，即i=1,2,3,…,N， 得到2N组PF分量和残余分量的集合。

(9)

4)计算所有PF分量和残余分量的平均值，即可得到LMD分解后的最终PF分量和残余分量。

(10)

(11)

式中：Pj(t)即为LMD分解得到的第j个PF分量；u(t)为最终的残余分量。

1.3 基于LMD的局部放电特征提取

局部放电信号的各个频率分量中包含着丰富的信息，LMD可以自适应地将局部放电信号分解为若干个位于不同频带的PF分量，但由于局部放电信号的序列较长，若不加处理直接进行PF分量的特征提取会损失局部的特征细节，使得提取的特征较为宏观，无法有效表征局放信号包含的关键信息。为了充分利用LMD分解后PF分量中包含的特征信息，首先将PF分量分割成一个个小片段，考虑每个片段内的特征。本文参考文献[16-17]中的特征参量选取方法，从PF分量每个片段内的能量、复杂度和变化趋势3个方面进行特征提取。对于信号片段的能量特征，最直接的方法是计算其能量值。但为了消除数值大小对后续分类识别的影响，本文选择信号片段与其所属PF分量的能量占比作为特征参量，定量反映信号能量的分布情况。时序信号的复杂度常用熵来表征，Renyi熵是香农熵的推广形式，适用范围更广；赫斯特指数(Hurst Exponent)是由H. E. Hurst最早提出的一种时间序列分析方法，工程上常用于评估时间序列的自相似性和长期依赖程度，因此可以反映信号的变化趋势。本文选择能量占比、Renyi熵、赫斯特指数作为特征参数，特征提取的具体过程如下。

1) 向预处理后的局部放电信号中加入成对的高斯白噪声进行集总分解，得到m个PF分量，记为Pm。

2) 设置片段长度，将每个Pm分割成n个等长的信号片段Pmn，Pmn表示第m个PF分量Pm分割产生的第n个信号片段。

3) 计算各个信号片段Pmn的能量占比。

(12)

式中：EPmn为信号片段Pmn的能量值；EPm为第m个PF分量Pm的能量值。

4) 计算各个信号片段Pmn的Renyi熵，得到相应的熵值Rmn， Renyi熵的计算公式如式(13)所示。

(13)

式中：a为Renyi熵的阶数，当a趋近于1时Renyi熵即为香农熵，本文使用2阶Renyi熵，即a=2；xi为时序信号各个点的幅值，i=1,2,…,n；p(xi)为信号每个点取值对应的概率，且∑p(xi)=1。

5) 采用重标极差(R/S)分析方法计算赫斯特指数，计算方法如下。

假设有时间序列ξ(t)， 其中t=1,2,3,…,N， 定义其均值序列为：

(14)

式中T=1,2,3,…,N。

序列ξ(t)的累计离差为：

(15)

式中t=1,2,3,…,T。

极差序列为：

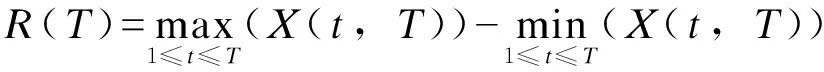
(16)

标准差序列为：

(17)

赫斯特推得极差与标准差的比值R(T)/S(T)(用R/S表示)存在如下关系。

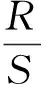
(18)

式中：a为常数；H为赫斯特指数。对式(18)两边同时取对数可得：

log(R/S)=Hlog(T)+log(a)

(19)

由于log(a)为常数，因此只需以log(T)为自变量、log(R/S)为因变量做回归分析即可得到赫斯特指数值H。计算各个信号片段Pmn的赫斯特指数，得到相应的值Hmn。

6) 根据时间顺序，将信号片段Pmn的能量占比Emn、Renyi熵Rmn、赫斯特指数Hmn分别合成能量占比序列Em、Renyi熵序列Rm和赫斯特指数序列Hm， 再将其合并，即可得到局部放电信号分解后分量Pm的特征矩阵Tm。

(20)

而对于单个局部放电信号来说，其最终特征矩阵T应由所有PF分量的特征矩阵合并得到。

(21)

2 基于LSTM的局部放电识别方法

2.1 LSTM的基本结构

LSTM本质上是循环神经网络(recurrent neural network，RNN)，与RNN相比，LSTM通过设置多个门控结构解决了RNN中存在的梯度爆炸和梯度消失问题，使其具备了训练、学习序列中长期依赖信息的能力[18]。遗忘门、输入门和输出门3个门控结构组成了LSTM的基本单元，结构如图1所示。

图1 LSTM的基本单元结构Fig.1 Basic unit structure of LSTM

遗忘门决定信息需要被丢弃还是保留，通过将上一个单元的输出ht-1和当前状态的输入值xt送入Sigmoid函数σ来判断是否保留上一个单元的状态量ct-1， 若Sigmoid函数输出0，则彻底删除ct-1， 若输出1，则完全保留ct-1， 遗忘门的输出记为ft。

输出门用来确定当前单元输出的信息。首先通过Sigmoid函数σ决定当前单元状态信息中需要输出的部分，当前单元的状态信息ct通过tanh函数激活后，再与Sigmoid函数σ的输出ot相乘即可得到当前单元的输出信息ht。相关公式如式(22)所示。

(22)

式中：xt为输入值；Wf、Wi、Wc、Wo为每个单元内各个门对应的权值；bf、bi、bc、bo为相应的偏置。

2.2 基于LSTM的局部放电识别模型

本文的局部放电识别模型及相应的流程结构如图2所示。

图2 局部放电识别模型结构Fig.2 Structure of PD identification model

本文建立的LSTM局部放电识别模型主要包括信号预处理、LMD分解、时序特征提取、LSTM模型训练和分类识别5个部分。采集到的局部放电信号首先通过小波包去噪的方法进行降噪预处理，再使用前文所述的成对高斯白噪声辅助的LMD分解和特征提取方法对预处理后的局部放电信号进行分解和时序特征提取。将特征矩阵汇总形成训练集带入LSTM模型中进行训练，为了实现不同类型局部放电信号的分类识别，在LSTM模型中加入了全连接层和Softmax层[19]，训练完成后将测试集数据代入训练好的模型，得到最终的识别结果。

3 盆式绝缘子典型缺陷局部放电实验

3.1 盆式绝缘子局部放电模型

参照550 kV盆式绝缘子的实际尺寸并将其结构适当简化，建立了平面化的小型盆式绝缘子模型，如图3所示。小型盆式绝缘子模型的外部为环氧树脂，其外径为120 mm，中间为直径60 mm的金属嵌件，嵌件中心有直径16 mm的通孔便于装配。在实验室中制作了带有裂纹、气泡、嵌件毛刺、表面金属颗粒的小型盆式绝缘子样品，其实物如图4所示。图中红圈处为缺陷所在的位置，其中裂纹缺陷主要集中在金属嵌件的周围，有少数裂纹从嵌件周围一直延伸到样品的外边缘，如图4(a)所示；气泡缺陷主要分布在样品环氧树脂部分的中间位置，如图4(b)所示；嵌件毛刺缺陷通过环氧浇注前在嵌件上预先附着金属尖端来实现，如图4(c)红圈处所示；表面金属颗粒缺陷通过在无缺陷的小型盆式绝缘子表面粘附铝箔来模拟，其中铝箔为边长为3 mm的正三角形，如图4(d)红圈处所示。

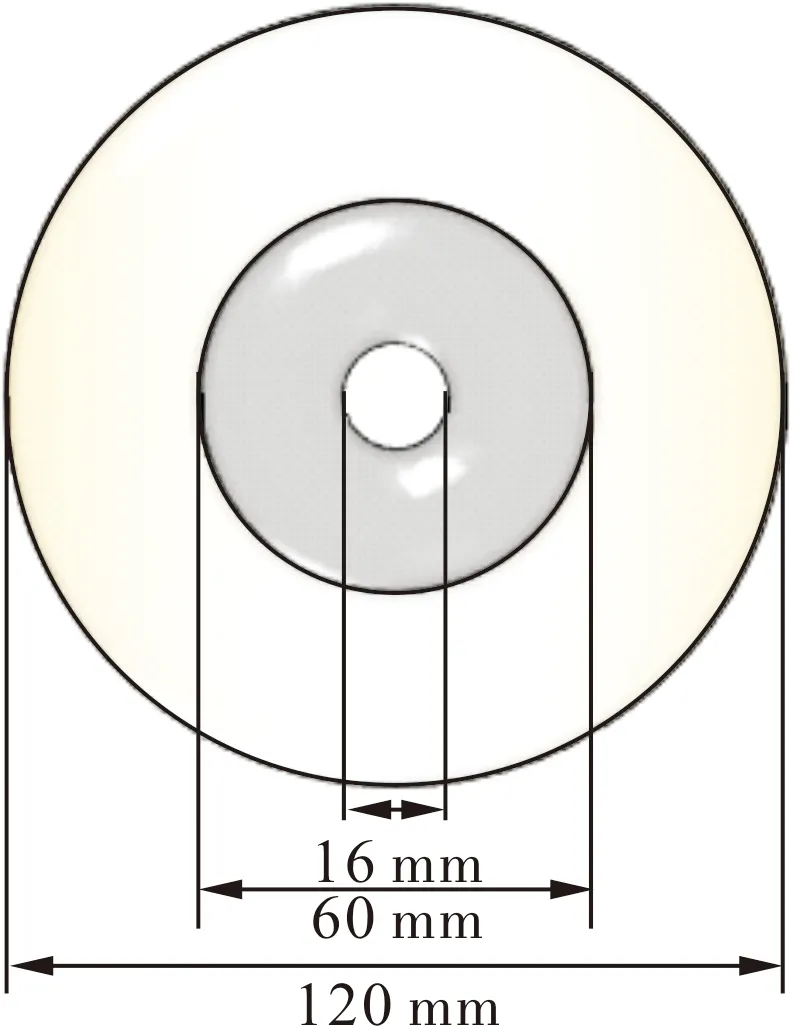
图3 小型盆式绝缘子模型结构图Fig.3 Structure diagram of small basin insulator model

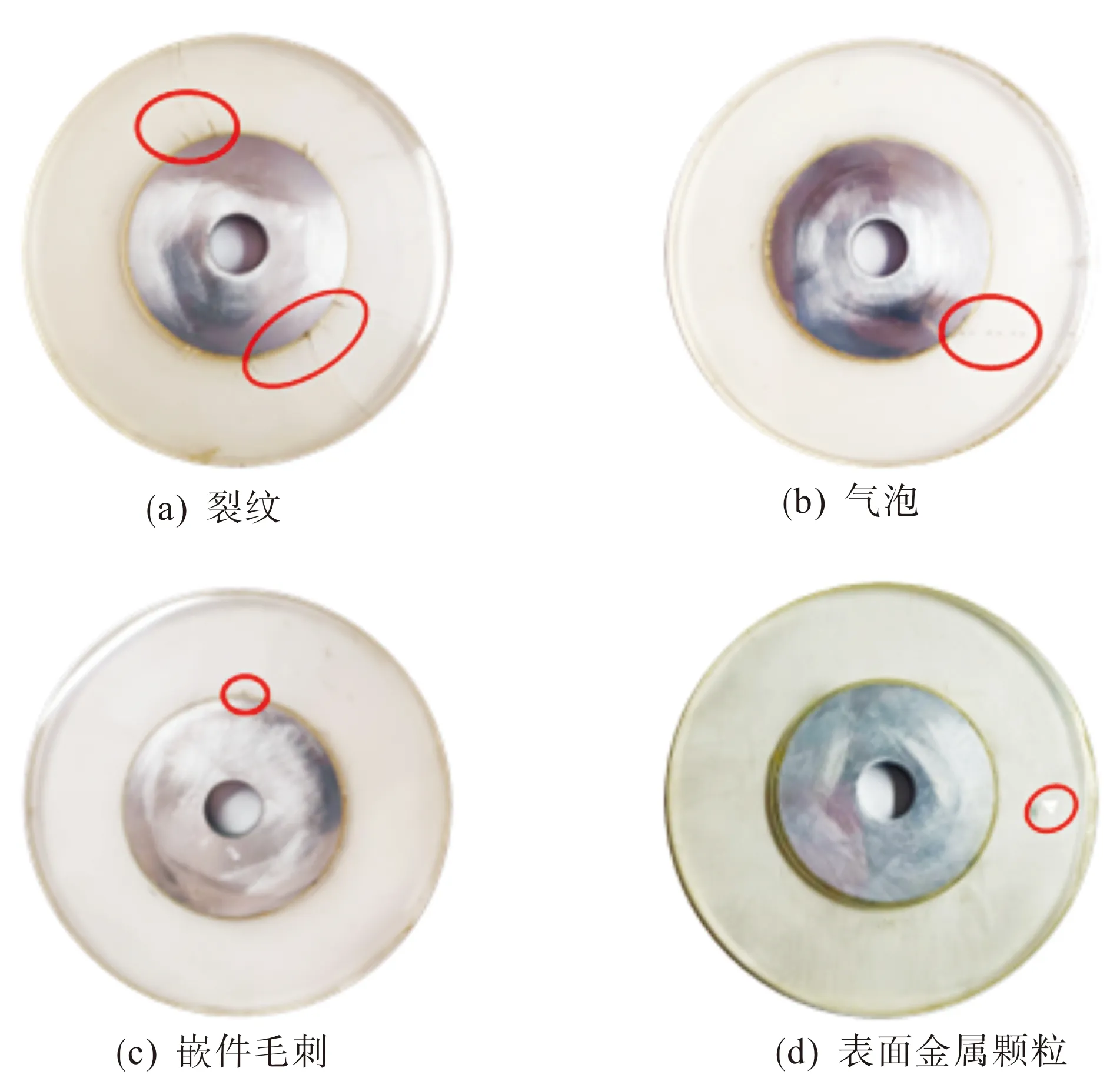
图4 小型盆式绝缘子实物图Fig.4 Pictures of small basin insulator

3.2 盆式绝缘子局部放电实验平台

为了模拟盆式绝缘子缺陷局部放电的实际工况，同时兼顾实验开展的便利性，在实验室中设计并建立了实验腔体，主要由亚克力腔体外壳、高压导杆、均压球、小型盆式绝缘子、接地金属环构成，其结构如图5所示。

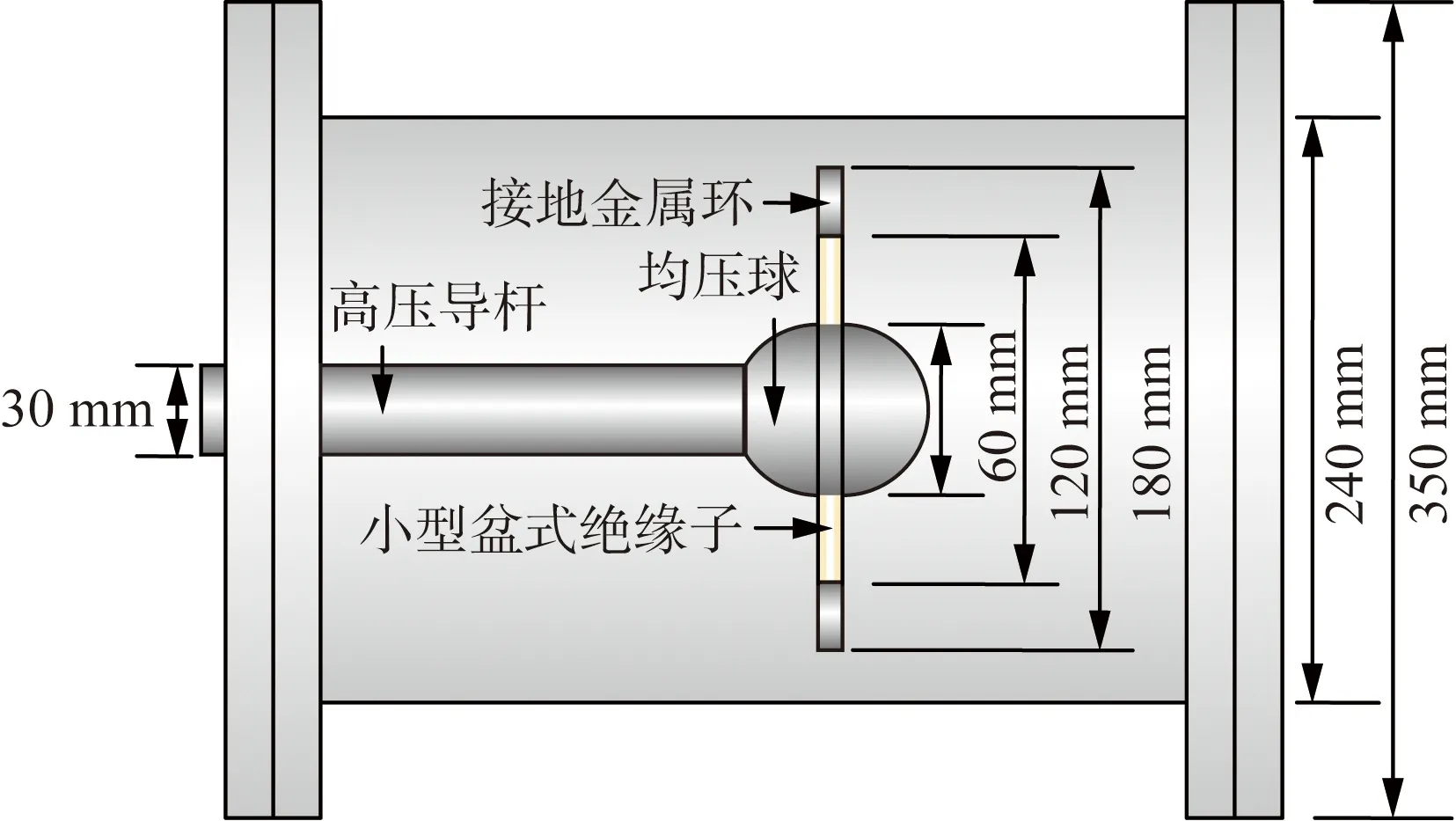
图5 实验腔体结构图Fig.5 Structure diagram of experimental chamber

实验回路如图6所示。其中T1、T2分别为调压台和YDTW10/100型无局放工频试验变压器，额定电压为100 kV，容量为10 kVA；R为限流电阻，C1、C2构成电容分压器，C3为耦合电容，Z为检测阻抗。采用接触式声发射传感器检测局部放电信号，其谐振频率为40 kHz，工作带宽为30～140 kHz，灵敏度大于80 dB，信号放大器的增益为60 dB。

图6 实验回路结构图Fig.6 Structure diagram of experimental circuit

将小型盆式绝缘子样品安装到实验腔体中，密封腔体后抽真空再充入0.3 MPa的SF6气体。实验时声发射传感器使用耦合剂粘在实验腔体的外壁上，使用泰克DPO5204B示波器(带宽2 GHz，最大采样率10 GS/s)的2个通道同时采集局部放电的超声波信号和电压相位信号。采用缓慢升压的方式直至示波器和局放仪上均出现稳定的局部放电信号，维持该电压并保存示波器上采集到的信号。

4 数据处理与和识别结果分析

4.1 局部放电信号的预处理

利用前述的实验装置与方法在实验室中采集大量不同缺陷的局部放电信号，并将其根据工频相位分成一个个完整工频周期内的信号，不同类型局部放电的时域信号如图7所示。

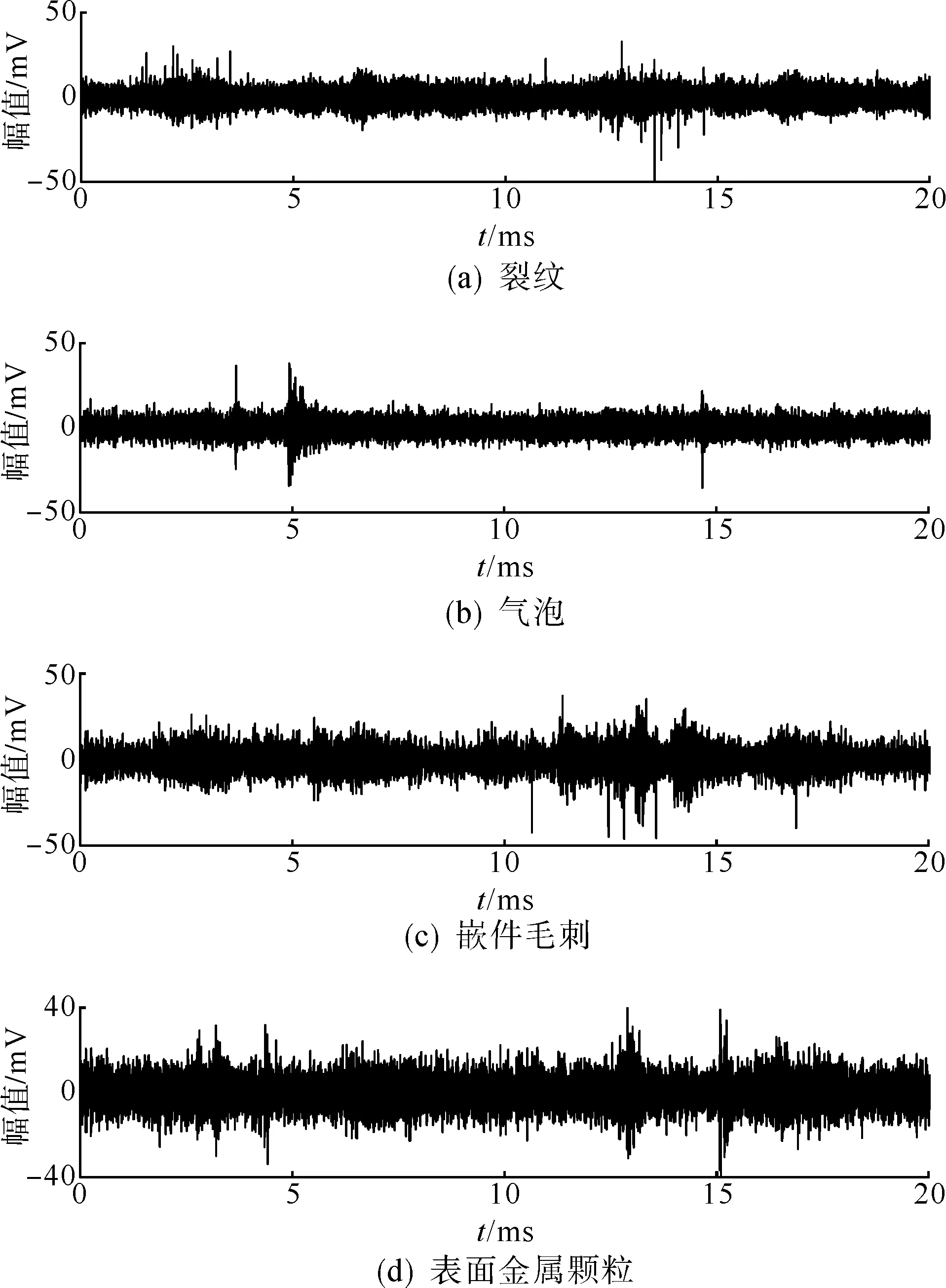
图7 4种局部放电信号的时域波形图Fig.7 Time domain waveforms of four types of PD signals

本文使用4层db10小波包分解对原始局放信号进行去噪预处理，其中阈值选择采用Stein无偏似然估计法。图8为一个裂纹缺陷局部放电信号去噪前后的波形对比。

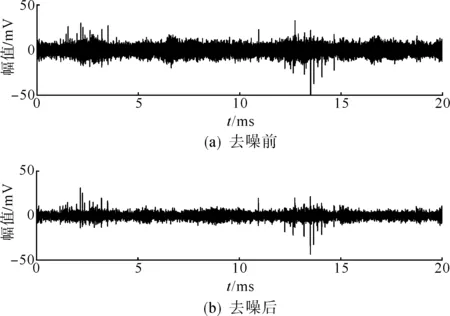
图8 裂纹缺陷局部放电信号去噪前后的时域波形图Fig.8 Time domain waveform of a PD signal of crack defect before and after denoising

4.2 局部放电信号的分解与特征提取

向预处理后的局部放电信号中加入正负成对的高斯白噪声，再使用LMD进行集总分解。本文加入的高斯白噪声幅值ε为0.2倍局部放电信号的标准差，集总分解次数为100次。仍以一个裂纹缺陷局部放电信号为例，经加噪和集总分解后的结果如图9所示。

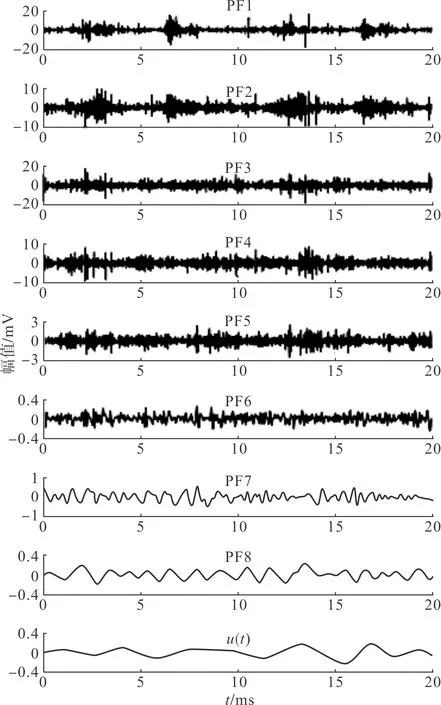
图9 裂纹缺陷局部放电信号分解结果图Fig.9 Decomposition results of a PD signal of crack defect

由图9可知，该裂纹缺陷局部放电信号最终被分解为8个PF分量，但从PF分量的波形和相应的幅值大小来看，前几个PF分量包含了局部放电信号的主要信息，如果对所有PF分量进行特征提取将产生大量无效的特征参数，不仅会增加计算负担，还会影响后续分类识别的正确率[20]。因此本文使用PF分量的能量占比作为选取主PF分量的评判标准，相应的公式为：

(23)

式中：Ei为PF分量Pi的能量占比；EPi为第i个PF分量Pi的能量值；EX为局部放电信号预处理后的总能量。

4种局部放电信号的PF分量能量占比如图10所示。从图中可知各类型局部放电信号的能量主要集中在前4个PF分量，因此选择前4个PF分量作为主PF分量。

图10 局部放电信号的PF分量能量占比Fig.10 Energy share of PF components of PD signals

此外，由于实验中采集的局部放电信号点数较多，若直接将分解得到的PF分量作为训练样本代入LSTM模型中进行训练，将导致训练时间大大增长，而且在很长的序列里进行反向传播可能会导致梯度消失，这样模型的可靠性会有所降低。因此设置了50、100、200、400、800共5个不同的片段长度，将主PF分量分割成等长的片段，计算每个主PF分量片段的能量占比、Renyi熵和赫斯特指数并形成特征矩阵T50、T100、T200、T400、T800。

4.3 局部放电的分类识别结果

从采集处理后得到的大量数据中随机选取4类各1 000组局部放电信号作为样本，按照8:1:1的比例随机划分训练集、验证集和测试集，即每类局部放电样本中训练集数量为800组，验证集和测试集各100组。

LSTM模型中相关参数的设置直接影响模型训练的效率和识别的正确率[21-22]。本文设置LSTM模型的隐藏单元个数为100，批尺寸(batch size)为80，采用Adam优化算法对模型进行训练[23]，其中训练的初始学习率(learning rate)设为0.001，为了防止出现无法收敛的情况，设定每训练10轮(epoch)将学习率衰减为原来的0.2倍，训练的最大轮数为50，训练过程使用英伟达GTX850 4GB GPU完成。

为了确定最佳的片段长度，使用不同片段长度下局部放电样本对应的特征矩阵T50、T100、T200、T400、T800进行训练和测试，对比了50、100、200、400、800共5个不同片段长度下训练集、验证集和测试集的识别正确率，如图11所示。

从图11中数据可知，随着片段长度的增大，训练集、验证集、测试集的识别正确率均有所提升，这是因为一方面片段长度较小时特征序列会相对较长，不利于LSTM模型的训练，另一方面由于片段长度较小，每个片段内包含的信息相对较少，无效的特征会增多，从而降低了识别正确率。当片段长度为800时，在训练集上的正确率达到了100%，验证集和测试集上的正确率均超过了99%，说明该片段长度下提取的特征能够很好地表征局部放电信号的主要信息，因此选择800作为最佳的片段长度。最佳片段长度下LSTM模型训练过程中训练集和验证集的正确率变化曲线如图12所示。

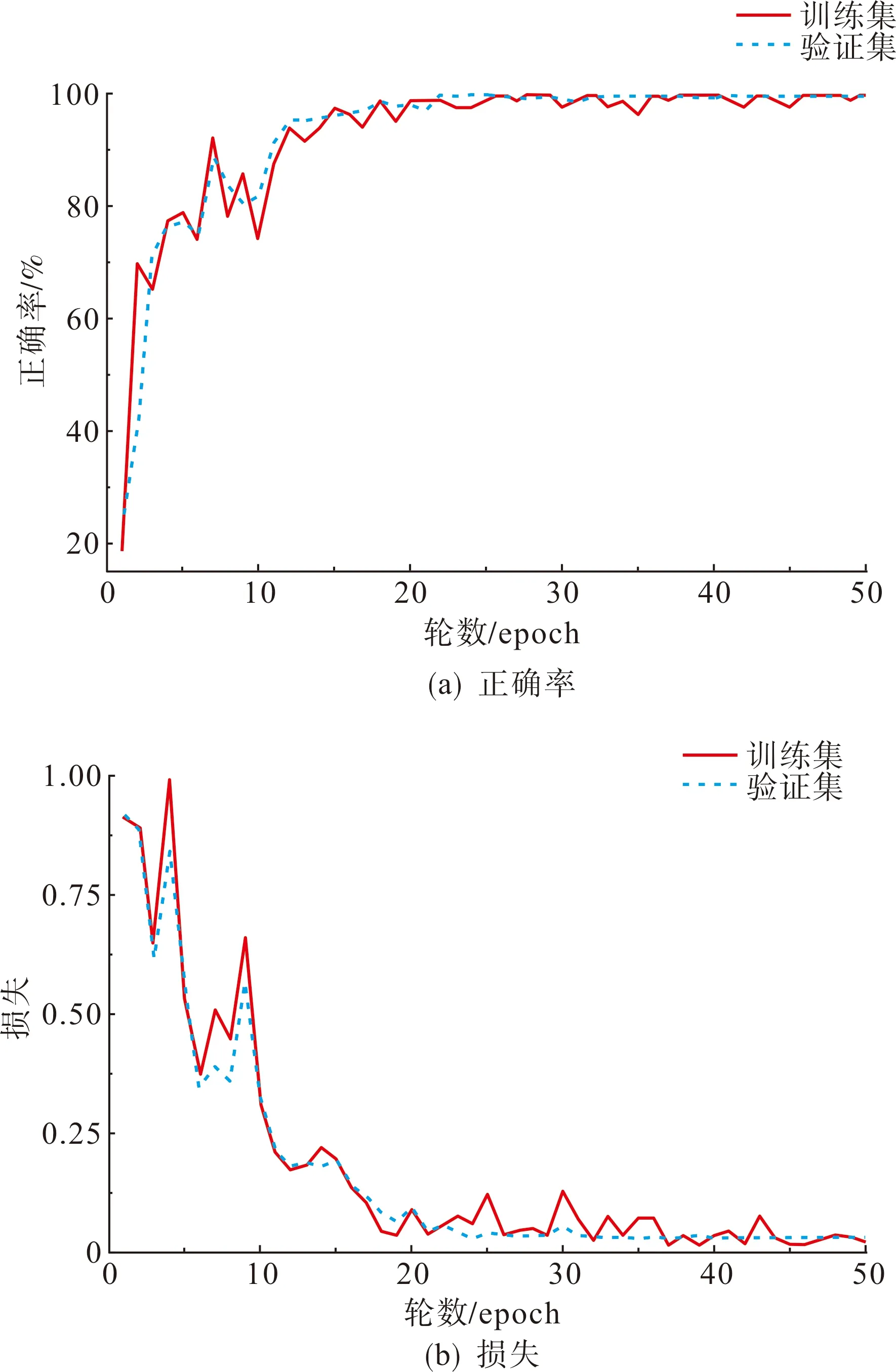
图12 最佳片段长度下训练过程中正确率与损失变化曲线Fig.12 Changing curves of the accuracy and loss in the training process under the optimal fragment length

从图12中可以看出，当训练开始时训练集和验证集的正确率约为20%，随着训练轮数的增加，正确率开始逐渐升高。经过20轮训练后，训练集和验证集的正确率逐渐趋于稳定，直至训练完成，此时训练集的正确率为100%，验证集的正确率为99.5%。虽然训练集上的正确率为100%，但验证集上的正确率没有出现下降的情况，同时从损失的变化曲线可以看出，随着训练的进行训练集和验证集上的损失都在逐渐下降，最终随着正确率的稳定而趋于平稳，因此没有过拟合的问题。测试集上各类局放信号的识别正确率如表1所示。

表1 LSTM分类识别结果Tab.1 Classification recognition results of LSTM

由表中数据可以看出，裂纹、气泡、嵌件毛刺、表面金属颗粒4种不同缺陷下的盆式绝缘子局部放电信号识别正确率较高，其中裂纹和表面金属颗粒缺陷下的局部放电信号识别正确率达到了100%，验证了本文提出的方法的可行性。

除了识别正确率，常用于评估分类效果的参数指标还包括混淆矩阵、精确率、召回率和F1分数。精确率(Precision)是被预测为某一类的所有样本中确实为该类别的样本所占的比例，召回率(Recall)是实际为该类别的样本中被预测为该类别样本所占的比例，F1分数则是两者的综合，其公式为：

(24)

LSTM分类结果的混淆矩阵如图13所示，各类缺陷分类结果的精确率、召回率和F1分数如表2所示。

图13 LSTM分类结果的混淆矩阵Fig.12 Confusion matrix for classification results of LSTM

表2 分类结果的精确率、召回率和F1分数Tab.2 Accuracy, recall and F1 score of classification results

从图13和表2中的数据可以看出，4种缺陷分类结果的精确率、召回率和F1分数均为较高水平，其中表面金属颗粒缺陷的识别精确率和召回率均达到了100%，说明本文方法下表面金属颗粒缺陷放电信号可以与其他3种信号完全区分，其他3种缺陷之间仅存在少量的误判，体现了本文方法的有效性。

为了进一步验证本文提出的基于LMD分解的特征提取方法的优越性，使用预处理后的局部放电信号不经过LMD分解直接进行特征提取，片段长度仍设置为800，使用相同设置参数的LSTM模型进行了训练和识别。

此外，统计参数是局部放电信号识别中常用的特征参量[24-25]，本文提取了最大放电量相位分布Hqmax(φ)、平均放电量相位分布Hqn(φ)、放电次数相位分布Hn(φ)图谱的24个特征，如表3所示，其中Sk为偏斜度，Ku为峭度，Pe为峰值个数，Asy为不对称度，cc为互相关系数，下标+代表正半周期，下标-代表负半周期。使用核主成分分析方法进行降维，使用降维后的特征参数带入支持向量机(SVM)进行训练和识别，选择C-SVC作为SVM模型，径向基函数作为核函数，训练时使用网格搜索算法对惩罚参数c和核函数参数g进行寻优，最终的分类结果如表4所示。

表3 统计参数Tab.3 Statistical parameters

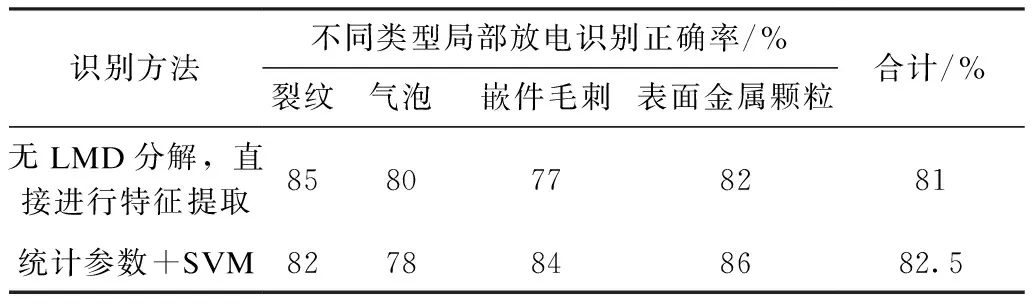
表4 不同识别方法的识别结果Tab.4 Recognition results of different recognition methods

由表4中数据可以看出，无LMD分解情况下的识别正确率超过了80%，表明本文选取的3种特征量能够较好地表征局部放电信号的主要信息。对比表1和表4，无LMD分解情况下的识别正确率远低于使用成对高斯白噪声辅助LMD分解的情况，主要原因是局部放电信号中包含多个不同频带的信息，如果直接对局部放电信号进行特征提取会导致所提取的特征无法很好地反映局部放电信号不同频带内的特性，从而降低了识别正确率。而基于统计参数和SVM的识别正确率为82.5%，同样远低于本文所提方法的识别正确率，这一方面是因为基于统计参数的特征提取方法需要提取的特征过多，降低了特征参数的代表性，另一方面统计参数主要反映了信号时域正负半周的波形特性，较为宏观，同时忽略了信号频域的信息。本文方法对位于不同频带内的PF分量进行片段分割后再提取特征，兼顾了局放信号的频域信息和时域的特征细节，因此取得了良好的识别效果，虽然特征提取部分的算法复杂度较高，牺牲了一定的计算性能，但整体的分类正确率有明显提高。

5 结论

本文针对盆式绝缘子典型缺陷的局部放电，在实验室中建立了盆式绝缘子局部放电实验平台并采集了大量数据，提出了一种基于LMD和LSTM的盆式绝缘子局部放电识别方法，使用该方法对采集到的信号进行分类识别，得到了如下结论。

1) 使用小波包去噪方法对局部放电信号进行降噪，在LMD分解前向信号中添加了成对的高斯白噪声，一定程度上抑制了模态混叠和端点效应。分析发现信号经LMD分解后的主要信息集中在前4个PF分量中，选择前4个PF分量作为主PF分量，并将其根据不同的片段长度进行分割，提取了每个片段的能量占比、Renyi熵和赫斯特指数形成特征矩阵。

2) 为LSTM模型设置了合理的参数，对比发现片段长度为800时正确率最高，测试集上的综合正确率达到99.25%，验证了本文特征提取与识别方法的可行性。

3) 对比无LMD分解直接进行特征提取、统计参数结合SVM两种识别方法，本文提出的方法对不同类型局部放电信号的分类正确率提升明显，因此具有一定的应用推广价值。