基于响应曲面法的大电流开关柜结构优化

2021-09-24陆彪汤凯陈德敏何胜方王昭

南方电网技术 2021年8期

陆彪，汤凯，陈德敏，何胜方，王昭

(1. 安徽工业大学建筑工程学院，安徽马鞍山243000；2. 马鞍山钢铁股份有限公司，安徽马鞍山243000)

0 引言

大电流开关柜[1]是电力系统输配电与电网维护的基础设备[2-4]。由于大电流开关柜内母线承载上千安培电流，实际运行的大电流开关柜因内部母线热损耗处于发热状态[5]。母线温升不仅影响大电流开关柜最大载流容量，而且高温升极容易改变大电流开关柜内绝缘材料的绝缘性能，降低大电流开关柜安全稳定输配送电流的能力[6-7]。因此，无论是前期优化设计，还是后期实时运行状态检测，均有必要针对大电流开关柜的温升及散热特性进行综合分析。

国内外学者针对大电流开关柜散热特性计算分析主要基于解析法、实验法和数值模拟法[8-10]。解析法是利用发热体表面能量守恒关系求解发热体表面平均温度，虽可以快速求解出发热体表面平均温度及揭示发热体传热机理，但计算结果精度低，且无法反映发热体“场”的分布[11-12]。因此，目前采用解析法求解大电流开关柜散热特性的应用较少。实验法虽可以精确分析大电流开关柜不同散热因素的散热规律，但实验成本高、周期长、人员误操作大。数值模拟法是利用“场”分布来求解发热体温度[13]。由于近年来计算机技术和计算流体力学的蓬勃发展，使得数值模拟法在大电流开关柜设计过程中得到了快速发展，数值模拟法的出现极大地降低了大电流开关柜的设计成本[14-16]。文献[17]采用数值模拟与实验相结合的方法，分析了母线间距对大电流开关柜温升的影响，求解结果显示母线间距对母线温升影响显著，而母线间距对大电流开关柜温升作用需综合考虑发热元件功率损耗与大电流开关柜冷却能力。文献[18]基于数值模拟在不同载流条件下分析了三相母线中B相母线温升随母线间距变化过程，结果表明母线间距太大或太小均会导致B相母线温升增大，在三相母线排列过程中存在最优间距。文献[19]利用数值模拟法分析了母线偏转角度对母线温升的影响，得出母线偏转角度影响开关柜内气流运动流向及对流散热能力，存在最优的母线偏转角度。文献[20]基于数值模拟与实验法分析了配电柜通风口风速对配电柜散热能力的影响，发现气流流速增大有利于发热导体周围气体快速排出配电柜，在配电柜通风口风速为3 m/s和6 m/s时，进线断路器上接线端子处温升分别降低28.6%、48.1%。文献[21]通过数值模拟分析不同入口速度对开关柜速度场和温升影响，结果表明，在入口速度低于0.9 m/s时，开关柜内气体流速缓慢上升，最高温度缓慢下降；在入口速度达到1.2 m/s时，开关柜内气流流速线性增加，最高温度急剧下降；在入口速度高于1.8 m/s时，开关柜内最高温度再次缓慢降低。

综上所述可见，大多数学者针对大电流开关柜散热特性分析均未进行多因素交互作用研究，仅进行了单因素分析。本文在综合考虑大电流开关柜对流效应和辐射效应的基础上，建立大电流开关柜热-流耦合数值模型，通过仿真结果与实验结果对比来验证模型的精确性及正确性。并结合响应面曲面法[22-23]可以连续对各个因素进行分析的特点，分析母线垂直间距、母线偏转角度和入口平均风速等因素之间的交互作用以及对大电流开关柜内发热导体B相母线表面平均温度的影响。并建立B相母线表面平均温度与各个因素之间的函数关系式，寻求B相母线表面平均温升降幅最大的大电流开关柜最优结构。

1 大电流开关柜数值建模

1.1 基本假设

为了便于分析，对大电流开关柜热-流耦合场作以下假设：

1)空气为理想气体，其物性参数除密度外均保持恒定；

2)近似稳态，以大电流开关柜三相母线温度达到稳定状态时进行求解；

3)大电流开关柜外壳及母线的密度、比热容、导热系数均为常数。

1.2 模型求解域

本文选取图1所述的大电流开关柜模型为分析对象(母线偏转角度为90 °)，大电流开关柜求解域由母线、大电流开关柜外壳及大电流开关柜内空气区域构成。

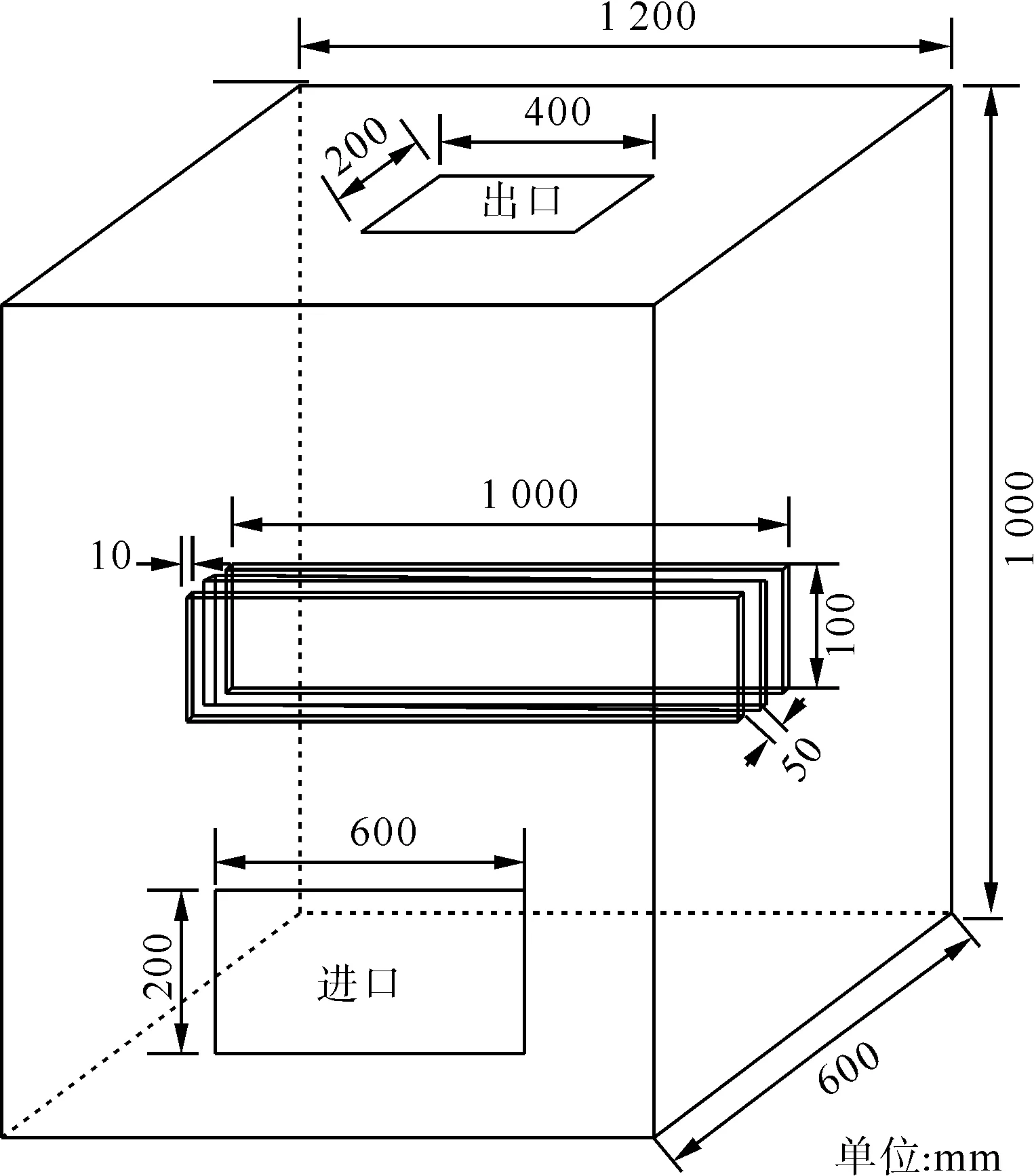
图1 大电流开关柜求解域Fig.1 Solution domain of large-current power switchgear

1.3 数学模型

计算流体动力学(Computational fluid dynamics，CFD)数值求解大电流开关柜热-流耦合场需要计算能量守恒、质量守恒、动量守恒、湍流及辐射方程。根据能量方程求解大电流开关柜内部温度场分布[24]。

(1)

(2)

式中：k1为母线导热系数，W/(m·K)；T为温度，℃；cp为等压比热容，J/(kg·K)；ρ为密度，kg/m3；W为速度矢量；qv为体积热源，W/m3；P1为单相母线功率，W；V为单相母线体积，m3；R为单相母线电阻，Ω；S为单相母线截面积，m2；L为单相母线长度，m；I1为单相母线负载电流，A；ρ0为单相母线电阻率，Ω·m；KJ、KL分别为集肤效应系数和邻近效应系数，通常截面为100×10母线的集肤效应系数为1.183，邻近效应系数为1.03[25]；t为单相母线表面平均温度，℃。

根据质量守恒及动量守恒方程求解大电流开关柜内不可压缩空气的速度场[24]。

(3)

(4)

式中：μ为动力黏度，Pa·s；P2为压力，Pa；g为重力加速度，m/s2。

(5)

式中：ρ为流体的密度，kg/m3；v为流体的速度，m/s。在开关柜内气流流速为0.12 m/s的工况下，大电流开关柜内部雷诺数计算如下：Dh=4×截面积/周长=(4×1.2×0.6)/(1.8×2)=0.8，Re=(1.06×0.12×0.8)/2.03×10-5=5 012.8>4 000。说明本模型柜内气流流态为湍流。因此可以采用k-ε湍流模型解决大电流开关柜内部设备附近散热强化问题[24]。

(6)

(7)

式中：Gk为平均速度梯度产生的湍流动能；Gb为浮力产生的湍流动能；Ym为可压缩湍流中过度扩散产生的波动；σk、σε分别为k-ε方程的紊流普朗特数；C2、C1ε、C3ε为常数。

为提高热-流耦合模型精度，需要考虑大电流开关柜热辐射，采用DO模型求解大电流开关柜内部辐射[24]。

(8)

式中：I为辐射强度，W/(m2·sr)；r为位置矢量；s为方向矢量；xr为路径长度，m；αrad为吸收系数；nr为折射率；σSB为斯特藩-玻尔兹曼常数，W/(m2·K4)。

1.4 边界条件

采用压力-速度耦合的Couple算法，求解大电流开关柜热-流耦合场分布。将大电流开关柜通风进口设置为速度进口[7]，本文通风进口风速是整个温升实验过程的平均值，通风出口设置为压力出口，在求解域边界上定义为混合辐射和自然对流，具体边界条件设置见表1。

表1 边界条件设置Tab.1 Boundary condition settings

1.5 网格无关性验证

为了避免网格变化对仿真结果的影响，在大电流开关柜负载电流为1 000 A的条件下，基于本文建立的热-流耦合算法求解三相母线表面平均温度随网格数变化过程，结果如图2所示。由图2可见，网格数量由40万增加到120万，三相母线表面平均温度随网格数增加先降低后趋于平缓，考虑数值计算精确性与周期性，选定网格数量为50×104。

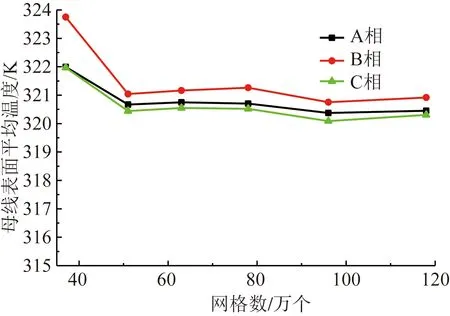
图2 三相母线表面平均温度随网格数变化过程Fig.2 Changing process of average temperature of the three-phase busbar surface against the number of grids

2 实验验证

为验证数值模拟的可靠性和准确性，设置环境温度为298.4 K，通风进口平均风速为0.24 m/s，负载电流为1 000 A，搭建大电流开关柜温升实验平台，实验原理图如图3所示，实物图如图4所示。

图3 大电流开关柜温升实验原理图Fig.3 Schematic diagram of temperature rise experiment of large-current switch cabinet

图4 大电流开关柜温升实验实物图Fig.4 Physical image of temperature rise experiment of large-current switch cabinet

分别利用忽略开关柜辐射效应的传统工程算法(传统工程算法的数学模型仅为式(1)—(7))、文中建立的热-流耦合算法及实验法，求解大电流开关柜三相母线温度并进行对比分析。表2为3种方法的计算结果。由表2可见，利用本文算法计算母线表面平均温度与实验结果之间最大误差为3.14%，传统工程算法与实验结果之间最小误差为8.24%。因此采用本文建立的热-流耦合算法相较于传统工程算法与实验结果更为吻合。

表2 不同方法母线表面平均温度Tab.2 Average busbar surface temperature with different methods

3 响应曲面设计

本文选择母线垂直间距、母线偏转角度及通风进口平均风速为影响因素。基于前人研究成果确定各因素取值范围，通过Design-Expert软件进行三因素三水平Box-Behnken设计，最终得到15组不同结构大电流开关柜组合，并对这15组结构分别建立物理模型、结构网格划分、数值模拟，从而得到不同结构的大电流开关柜内B相母线表面平均温度，表3与表4分别为响应曲面设计的因素水平与B相母线表面平均温度，X1为母线垂直间距(其变化过程如图5所示)、X2为母线偏转角度、X3为通风进口平均风速。

图5 母线垂直间距变化过程Fig.5 Changing process of busbar vertical space

表3 因素水平Tab.3 Factors level

表4 三因素数值计算结果Tab.4 Three-factor numerical calculation results

由表2可知，三相母线中B相母线表面平均温度最高，因此对B相母线表面温度监测更具意义。通过表4的数据，利用响应曲面法进行多元回归拟合分析，建立目标函数B相母线表面平均温度和X1、X2、X3的二次多项式回归方程，如式(9)所示。

(9)

式中：YT为响应值；X1X2表示母线垂直间距和母线偏转角度交互作用；X1X3、X2X3意义与之相同。

表5为基于回归方程得到的方差分析表，其中F检验值对应显著水平P值，常用来反映模型和各因素对响应值的显著性。一般认为P<0.05时，该因素对目标函数值影响显著。

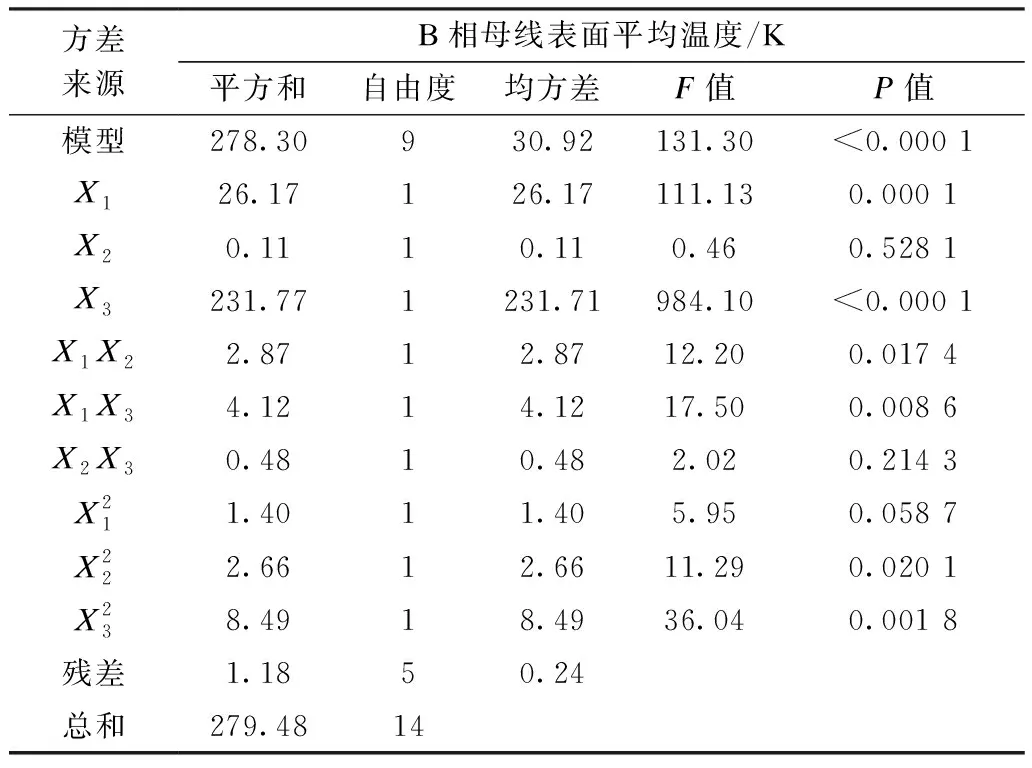
表5 响应曲面优化设计回归方程方差分析Tab.5 Variance analysis

4 结果分析

图6 残差的正态概率分布图Fig.6 Normal probability distribution of residuals

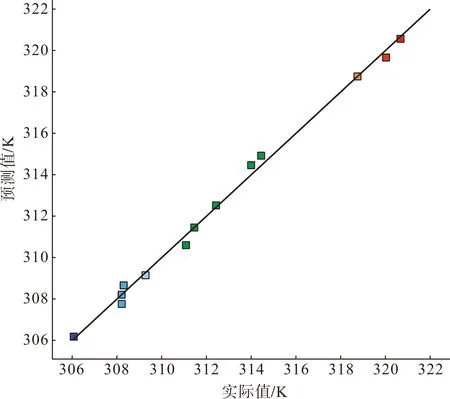
图7 预测值与实际值分布图Fig.7 Distribution of predicted and actual values

图8显示了在通风进口平均风速为1.24 m/s条件下，母线垂直间距和母线偏转角度对B相母线表面平均温度的交互影响。由图8可知，B相母线表面平均温度随着母线垂直间距的增大而降低，并且在母线偏转角度较小时的B相母线表面平均温度的降低速率小于母线偏转角度较大时的降低速率。这是因为在通风进口平均风速一定的条件下，母线垂直间距越大，相邻母线之间的热耗散相互影响越小，B相母线对流散热通道越大，所以B相母线表面平均温度随着垂直间距增大而降低。此外，由于在母线偏转角度较小时B相母线与周围环境之间散热气流相较于母线偏转角度较大时，更难以在短时间内通过通风出口迅速排出，因此，在母线偏转角度较小时，B相母线表面平均温度的降低速率小于母线偏转角度较大时的降低速率。

图8 垂直间距和偏转角度对母线表面平均温度交互影响Fig.8 Interactive effect of vertical spacing and deflection angle on the average surface temperature of the busbar

同理，当通风进口平均风速为1.24 m/s时，在母线垂直间距较小时，母线偏转角度对B相母线表面平均温度无显著影响；在母线垂直间距较大时，B相母线表面平均温度随母线偏转角度的增大呈现先降低后增大的现象。上述现象是因为在母线垂直间距较小时，由于相邻母线的阻挡，由通风进口进入大电流开关柜内部的冷气流，无法与B相母线进行直接热量交换；而在母线垂直间距较大时，未受相邻母线阻挡的B相母线在偏转角度由小变大的影响下，与通风进口进入的冷空气热交换时间呈先增大后减小的变化。基于上述分析可知，在通风进口平均风速固定的条件下，母线垂直间距对B相母线表面平均温度的影响大于母线偏转角度对B相母线表面平均温度的影响。

图9为在母线垂直间距为100 mm条件下，母线偏转角度和通风进口平均风速对B相母线表面平均温度的交互影响。由图9可知，母线偏转角度较大或较小时，B相母线表面平均温度都会随着通风进口平均风速的增大而减小，并且在不同母线偏转角度下B相母线随通风进口平均风速变化的降温速率基本相同。这是因为增大通风进口平均风速B相母线对流换热能力加强，母线偏转角度对B相母线表面平均温度的影响较小。

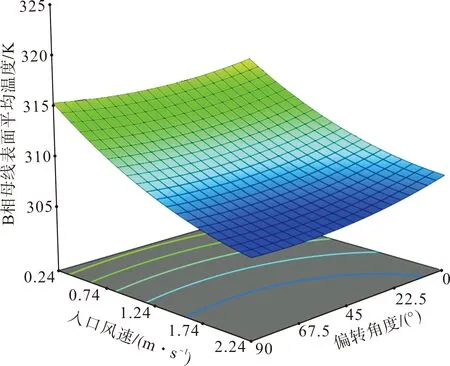
图9 偏转角度和入口平均风速对母线表面平均温度交互影响Fig.9 Interactive influence of deflection angle and inlet wind speed on the average surface temperature of the busbar

同理，当母线垂直间距为100 mm时，B相母线表面平均温度会随着母线偏转角度的增加先降低后上升。这是因为在通风进口平均风速一定的情况下，随着母线偏转角度的增大，B相母线与外界冷空气热交换时间呈现先增大后减小的趋势，但整个过程降温幅度较小。由此可见，在母线垂直间距固定条件下，通风进口平均风速对B相母线表面平均温度的影响比母线偏转角度对B相母线表面平均温度的影响更为显著。

图10显示在母线偏转角度为45 °条件下，母线垂直间距和通风进口平均风速对B相母线表面平均温度交互影响。由图10可知，B相母线表面平均温度随着通风进口平均风速增大而降低，且在母线垂直间距较大时对B相母线降温速率小于母线垂直间距较小时对B相母线降温速率。这是因为在母线垂直间距较大时受相邻母线之间热耗散影响，与周围环境温差小于母线垂直间距过小时。因此，母线垂直间距过大时B相母线降温速率小于母线垂直间距过小时B相母线降温速率。

图10 垂直间距和入口平均风速对母线表面平均温度交互影响Fig.10 Interactive influence of vertical spacing and inlet wind speed on the average surface temperature of the busbar

同理，当母线偏转角度为45 °时，B相母线表面平均温度随母线垂直间距的增大而降低，且在通风进口平均风速为2.24 m/s时的降温速率小于通风进口平均风速0.24 m/s时降温速率。这是因为母线垂直间距过小，影响B相母线散热通道，空气热传导影响增大，热阻增大，母线垂直间距增大有利于提高B相母线对流散热能力。此外，由于母线垂直间距过大时B相母线与周围环境之间温差小于母线垂直间距过小时，导致B相母线在母线垂直间距过大以及过小处降温速率出现差异。

同时，为了验证响应曲面法用于大电流开关柜结构优化的有效性，基于Design-Expert软件进行数据分析，通过上述3种因素对B相母线表面平均温度的显著性，进行优化后的模型与初始实验模型(即图1所示大电流开关柜结构)中B相母线表面平均温度的对比，并选取优化后的模型进行仿真验证，对比结果见表6。

表6 优化后模型与优化前模型的B相母线表面平均温度对比Tab.6 Comparison of B-phase busbar surface average temperature of the model before and after optimization

由表6可知，B相母线表面平均温度优化后降低了5.1%。为了更直观地说明优化后模型的优越性，利用Kim M J提出的母线节能率指标进行对比分析。其节能率计算公式如式(10)—(11)所示[26]。

ρk=0.068×T+15.7

(10)

(11)

式中：ρk为母线电阻率，Ω·m；ρ1为优化前母线电阻率，Ω·m；ρ2为优化后母线电阻率，Ω·m；η为母线节能率。优化前后的模型中B相母线表面平均温度分别为322.34 K(即49.19 ℃)、305.84 K(即32.69 ℃)，从式(10)中可得ρ1=0.068×49.19+15.7=19.045；ρ2=0.068×32.69+15.7=17.923。

从式(11)可得母线优化前后节能率的变化为：η=100×(19.045-17.923)/19.045=5.89%。

因此，可知母线优化后节能率提高了5.89%。