考虑交流馈入和稳态运行条件的柔性直流电网故障电流分析方法
2021-09-24孙银锋熊欣王振浩王威儒
孙银锋,熊欣,王振浩,王威儒
(现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林132012)
0 引言
基于模块化多电平换流器(modular multilevel converter,MMC)的高压柔性直流电网具有电压、容量等级易于扩展,谐波含量低,运行损耗小等诸多优点[1-2],并且在大规模新能源并网、电网互联[3-4]、电能质量控制、直流电网潮流控制[5]等方面具有广阔的应用前景。随着MMC在高电压、大容量、远距离输电领域的快速发展,架空输电以其经济性优势成为必然选择。对于基于架空线的柔性直流电网,直流线路故障保护已成为一项重要的研究内容[6]。与交流输电系统相比,直流输电系统的阻尼和响应时间常数较小,一旦发生直流故障,故障电流可以在很短的时间内上升到很高的值,严重影响设备甚至系统的安全稳定性[7-8]。考虑到换流站闭锁的不利影响以及换流站的容量和成本,工程上多采用半桥式换流器拓扑,而利用直流断路器在换流站闭锁前实现故障切除。然而,为了设计能够快速开断较大故障电流的直流断路器,必须对换流站闭锁前的短路电流进行计算,分析直流故障电流的关键影响因素及其在直流电网中的变化和传播机理。
文献[9-11]针对两端直流系统极间短路故障建立了直流侧电容的放电等效模型,并等值计算了故障电流,但未计及交流馈入(直流侧发生短路故障后交流侧持续馈入故障点的能量)的影响。文献[12-13]在双极直流电网等效网络模型基础上,提出了一种通用的极间短路故障电流计算方法,分别建立了故障前柔性直流电网的初始矩阵方程组和故障后该柔性直流电网的修正矩阵方程组,从而成倍地提高计算效率,并对各种工况下的柔性直流电网短路电流暂态特性进行了定量分析,但无法揭示故障电流与各参数之间的内在联系。文献[14]考虑了交流电流对子模块桥臂电流的影响,交流侧馈入等效为三相短路电流,而直流侧线路故障电流仍为纯电容放电电流的计算方法。文献[15]计及交流侧馈入和换流器控制的影响,以换流器能量变化作为切入点,采用递推方法进行短路电流计算,得到的短路电流计算结果更加精确,但无法明确交流侧馈入对故障电流的影响。
综上,目前对于直流故障电流的研究较少涉及交流侧的馈入问题,在故障电流的计算中忽略交流侧馈入,结果将会产生一定的误差,不利于直流设备的准确选型、精确控制和整定计算;当大规模风电、光伏等可再生能源接入柔性直流电网,特别是考虑到可再生能源的低电压穿越或者故障穿越策略,在故障工况下将可能持续向故障点馈入电流,交流馈入情况更值得关注。而将交流影响纳入直流短路电流计算的方法无法得到直流短路电流准确解析式,在量化分析换流站注入功率和直流电网故障前线路稳态潮流变化对于故障电流的影响方面尚属空白。
因此,本文首先建立了计及交流馈入的MMC换流器数学模型,将交流侧馈入作为受控直流电流源纳入直流电容放电计算中,对受控直流电流源进行等效计算,并引入交流注入功率这一变量,得到双端柔性直流系统单极接地故障时故障电流的精确表达式,然后利用灵敏度分析方法,明确两端MMC-HVDC交流注入功率波动对故障电流的影响。进而,将上述分析方法扩展至N个节点的柔性直流电网,利用潮流的负荷矩法和分流定理分析出直流电网初始线路潮流(指故障发生时刻线路的初始潮流)波动对于直流线路故障电流的影响。最后,以张北柔性直流电网实际工程为例对本文方法进行了验证。
1 计及交流馈入的直流故障电流计算等效模型
如图1所示的双极系统可以有效提升柔性直流输电系统的功率容量和电压等级,当某一极母线发生故障或者某个换流器出现故障时,只影响故障极和与故障极相连的换流器,对于健全极的影响很小,提高了系统运行的可靠性和安全性。

图1 双极MMC换流站系统结构图Fig.1 Structure diagram of a bipolar MMC converter system
图1中Udcp、Udcn分别为MMC直流正负极与中性线间电压。考虑到实际情况下单极接地故障发生的概率要比极间短路故障高得多,且直流线路极间短路故障可以等效为正负极各自发生单极接地故障,故本文着重分析单极接地故障的情况,此时与单极结构MMC的双极短路情况一致。为了方便阐述,本文以正极接地故障为例,详细拓扑结构如图2所示。图中,每个桥臂的电压和电流分别表示为urj和irj(下标r=p、n,分别表示上下桥臂;下标j=a、b、c,分别表示a、b、c三相,下同)。mrj和uΣrj分别表示每个桥臂的调制信号和桥臂子模块电容电压的和。MMC输出的交流电流表示为ivj。交流电网公共连接点(point of common coupling,PCC)处的电压表示为ugj。联接变压器的漏感和电阻分别用LT和RT表示。桥臂电感和电阻分别用Larm和Rarm表示。直流正极电压和直流电流分别用udcp和idc表示。所有电气量的方向已在图中标注。
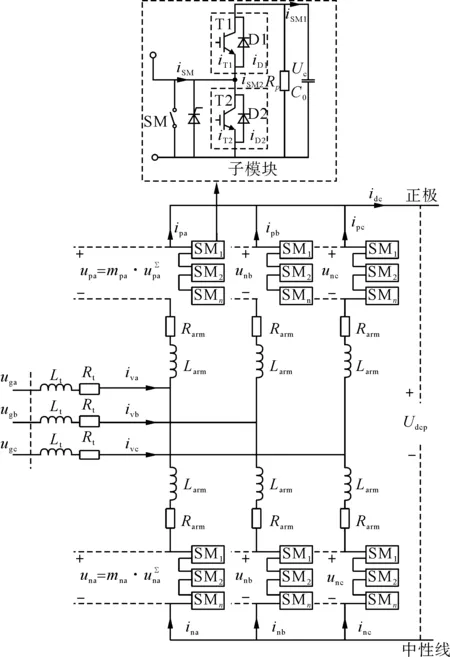
图2 MMC换流站正极详细拓扑结构图Fig.2 Detailed topology of MMC converter station positive pole
直流侧发生短路故障的情况下,在MMC闭锁前的短时间内,在电容均压控制作用下,子模块电容通过故障点迅速放电;此时,MMC直流侧故障电流特性主要由子模块电容放电决定[16-17];虽然在故障初期,交流侧电压峰值小于直流电压幅值,无法直接向故障点馈入电流,但随着直流电容放电过程的进行,直流侧电压降低,交流侧对故障点的馈入电流也会逐渐增大。分析直流单极接地的故障电流须建立计及交流馈入的直流等效模型。
在系统平衡的条件下,根据基尔霍夫电压定律(Kirchhoff voltage law,KVL)可得单相电路上、下桥臂的电压方程[18]分别如式(1)所示。
(1)
MMC的上下桥臂子模块的投入比分别为:
(2)
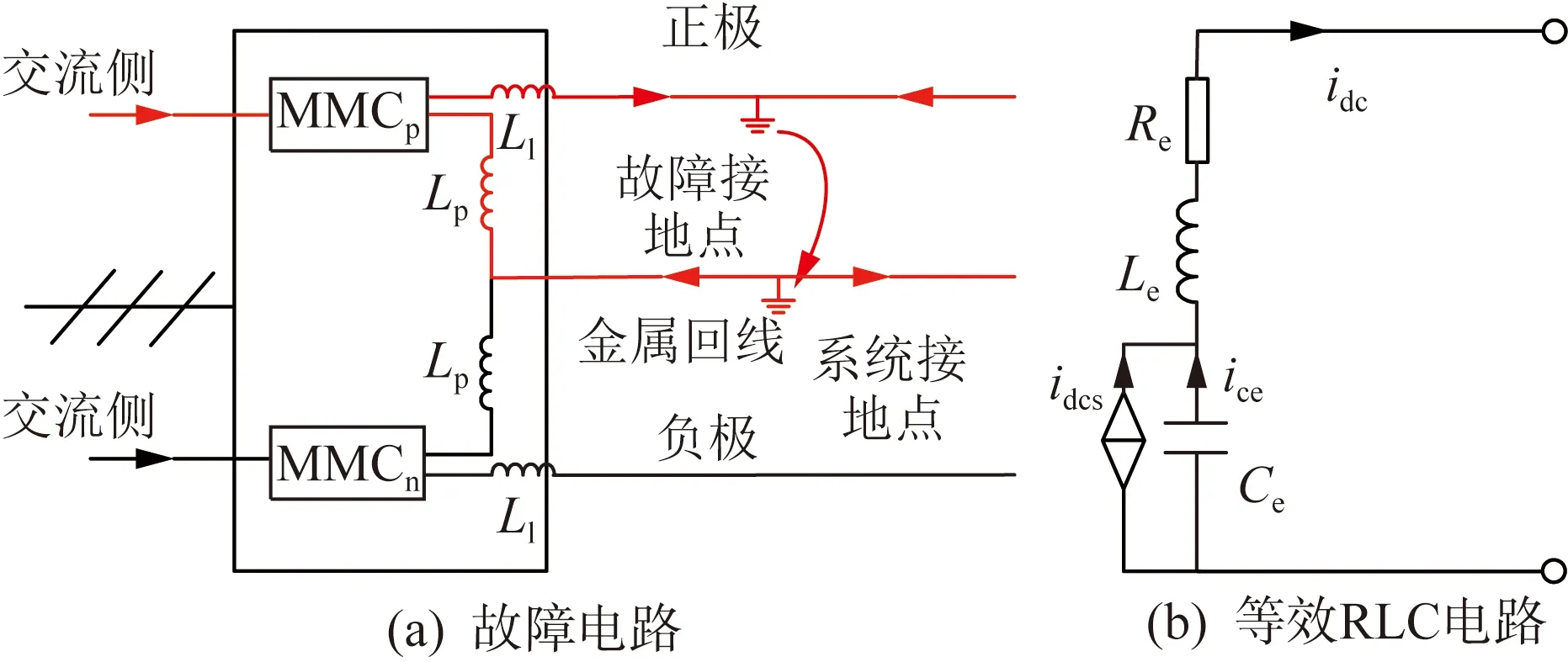
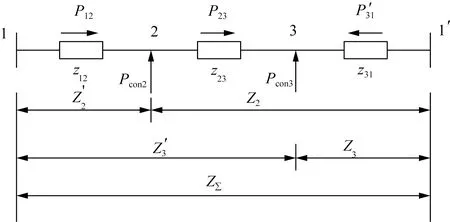
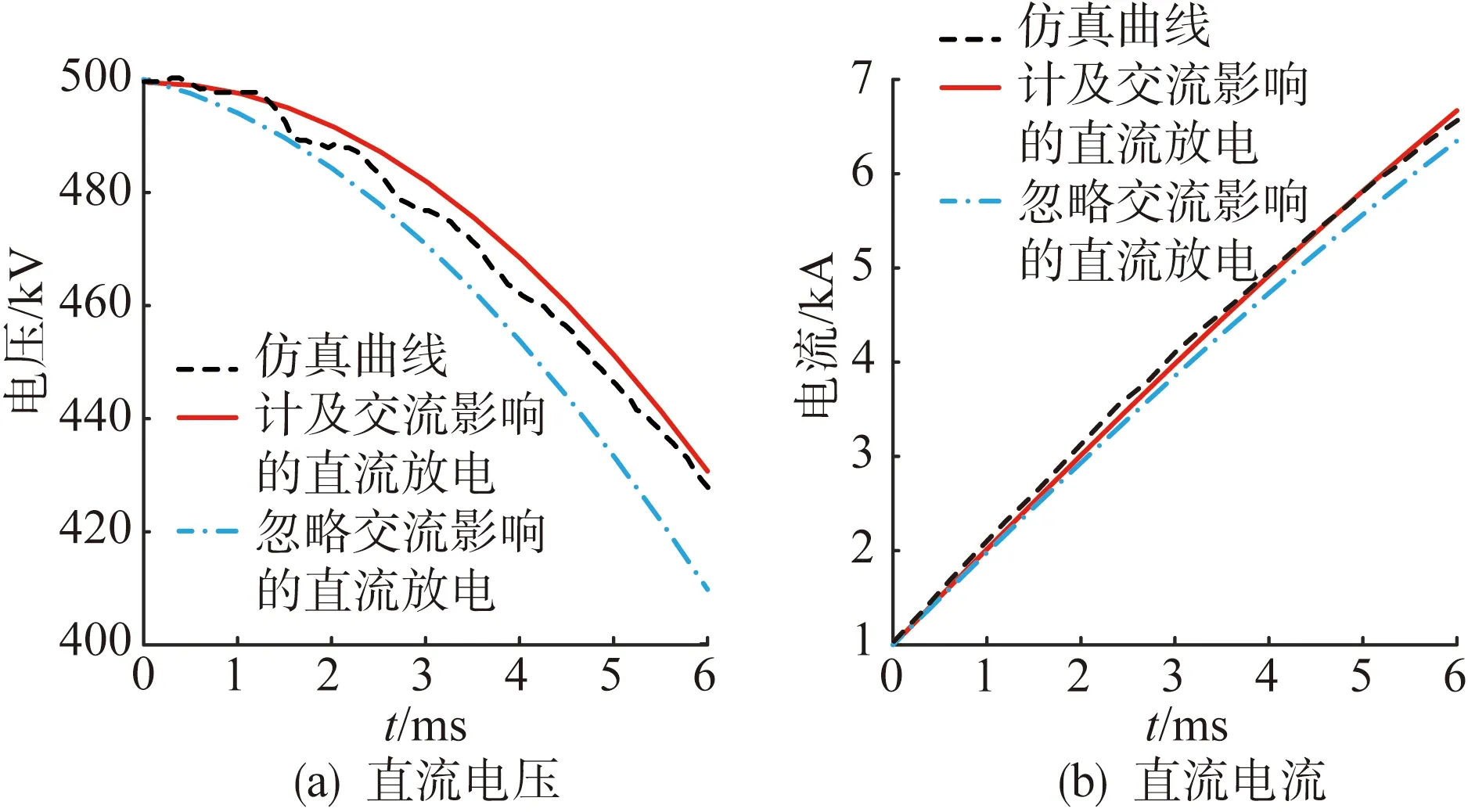
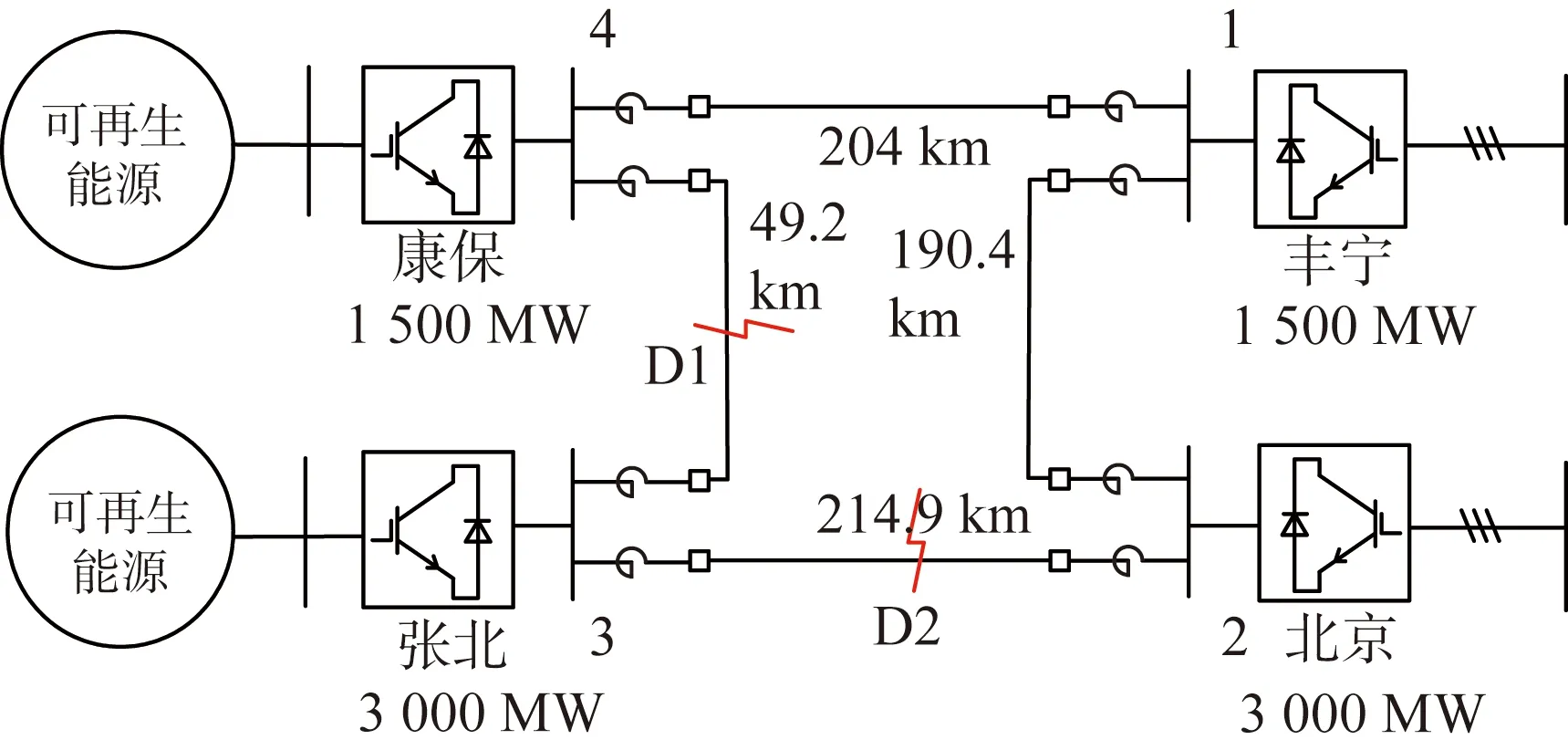
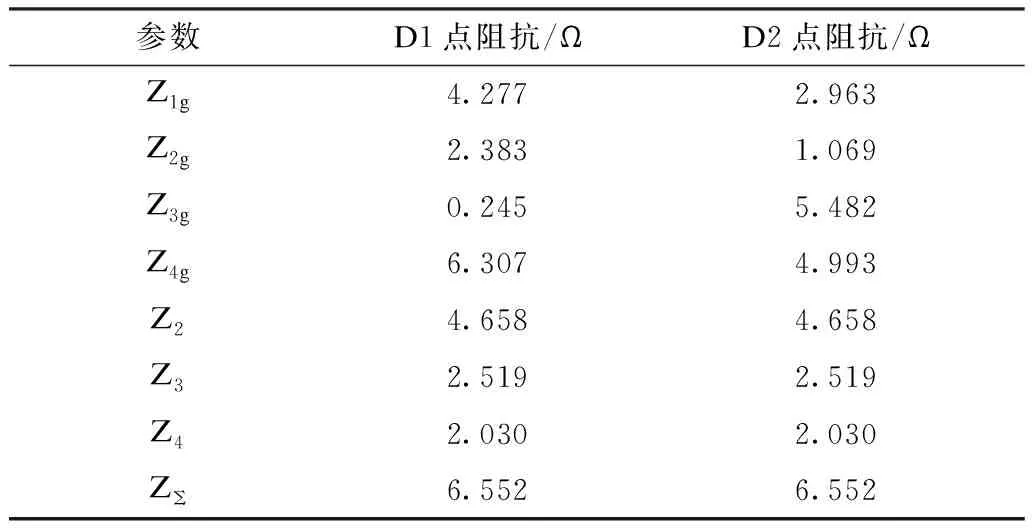
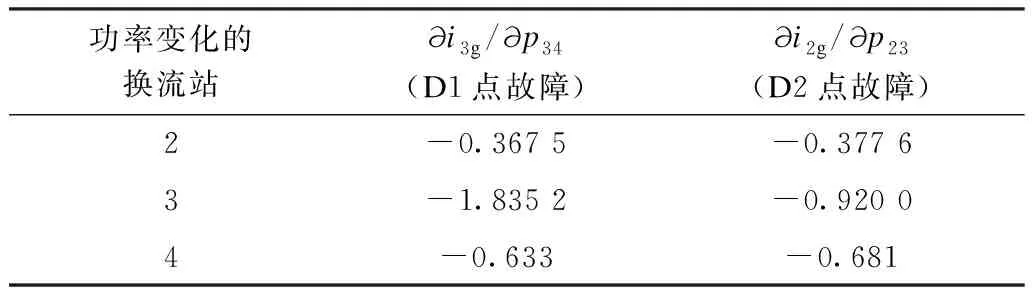
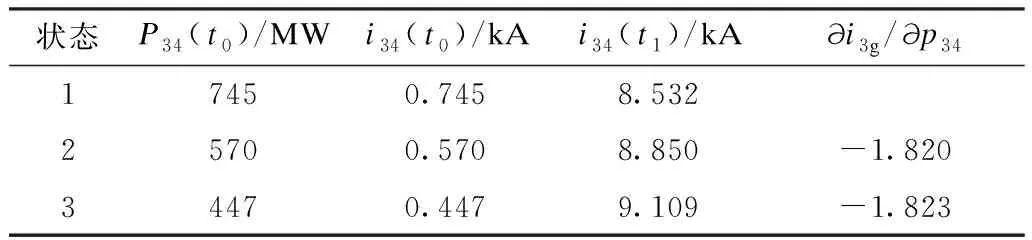
式中:M为调制比(0 根据图2中电流电压关系可得: (3) 式中:uvj为MMC的j相输出电压,也称为MMC的内电势;ucomj为j相上下桥臂的共模电压;icirj为j相的环流。 由式(1)和式(3)可得MMC直流侧等效电路动态特性的数学方程为: (4) 首先对MMC的直流侧动态方程式(4)进行三相叠加可得: (5) 又由图2可知,三相环流之和与直流电流关系为: (6) 定义MMC的等效电容电压uce为: (7) 将式(6)—(7)代入式(5),即可初步得到MMC直流侧等效电路模型,如式(8)所示。 (8) 为了进一步建立计及交流影响的直流等效模型,在此引入式(9)—(10)描述MMC的桥臂输出电压与桥臂所有子模块电容电压之和的内在关系[19]。 (9) (10) 将式(11)代入MMC等效电容电压uce表达式(7),则有: (12) 对上式进行求导并结合式(10),可得: (13) 进一步地,将式(2)代入上式进行化简,可得物理意义更为直观的表达式。 式中:Ce=6C0/N被定义为MMC的等效电容;C0为换流器子模块电容值;Pcon为换流站注入功率。 由式 (14)可得: (15) 令 idcs=pcon/2uce (16) idcs等效MMC直流侧等效电路的受控直流电流源,其大小由换流站注入功率和MMC的等效电容值决定。 在系统稳态运行状态下,MMC电容充放电维持动态平衡,电容电压波动比较小,电容电流ice近似为0,即: (17) 结合式 (14)和式(17)可得: idcs=pcon/2uce=idc=pdc/udc (18) 式中:pdc为换流站直流侧有功功率;udc为直流极间电压。 同时,由于MMC桥臂电阻取值较小,可忽略MMC内部损耗,再根据交直流侧功率平衡原理可得: (19) 式(19)理论分析的结果与式(18)数学推导的结果相同,验证了受控直流电流源公式的正确性。 以柔性直流电网正极直流线路发生短路故障为例,如图3(a)所示,故障电流通过MMCp、正极线路、线路电抗、故障接地点、直流系统接地点、金属回线和极线电抗Lp形成闭合回路。换流站闭锁前,MMCp所有子模块电容均通过该回路迅速放电的同时,交流侧对子模块电容持续充电,起到支撑作用。此时,交流侧电源、正极换流器MMCp、线路电抗和极线电抗可等效为如图3(b)所示的RLC电路。 图3 单极接地故障等效电路图Fig.3 Equivalent circuit diagram of single pole earth fault 图中Le为放电回路的等效电感,Re为放电回路的等效电阻。 MMC等效通路的KVL方程为: (20) 等值电路中的各个元件参数相当于换流器各相上下桥臂元件串联后在相间并联的结果,即: (21) 式中:Ll为直流线路的限流电感;Lp为换流器与中性线之间的极线电抗;Ron为IGBT的通态电阻;Rg为直流接地的过渡电阻。 故障情况下,控制中内外环控制器的比例积分参数以及控制器所配置的限幅环节将对换流站注入功率pcon(t)产生影响,无法保持在设定值,由于故障初期6 ms(考虑直流断路器6 ms内动作,本文探讨的张北柔性直流电网过流保护定值在5 kA左右[20],经计算换流器尚未闭锁)内换流站注入功率变化不大,且由第4节算例分析2中可以得出注入功率的变化对故障电流影响较小,可近似为pcon(t0)≈pcon(t)。 但电容电压uce会随着电容放电逐渐降低,受控直流电流源为一个非线性受控电流源。而故障电流的求解方程为四阶微分方程,为明确交流馈入对故障电流的影响,本文将交流控制电流源等效为线性电流源,进一步对故障电流求解方程降阶处理。通过对式(20)进行求解可得t1时刻受控直流电流源idcs的值,已知初始和故障后6 ms的直流电流源的值,然后进行线性处理。 (22) 式中:idcs(t0)为故障初始电流源电流;idcs(t1)为t1时刻的电流源电流;K为等效的线性电流源斜率。 针对柔性直流系统直流侧单极接地故障,将式(22)代入式(20)中可以得到计及交流馈入的等值通路二阶KVL方程。 (23) 求解式(23)二阶微分方程可得式(24)。 (24) 其中 (25) 式中:α为阻尼系数;ω0为无阻尼振荡频率;ωd为衰减震荡频率;β为常数。 直流换流器出口故障电流idc(t)为直流电容电流与交流馈入电流之和,即: 通过上式对换流站注入功率求偏导,可以得出t1时刻换流站注入功率对直流出口故障电流的灵敏度值η。 (27) 第2节已求得双端柔性直流系统换流站注入功率波动对于直流故障电流的影响,而直流电网的潮流分布由各换流站注入功率和直流线路阻抗决定。本节将通过潮流负荷距方法和分流定理,进一步分析柔性直流电网初始线路潮流波动对直流线路故障电流的影响。针对直流电网某一换流站注入功率的变化引起的潮流波动对直流线路故障流的影响进行分析,除了功率变化的换流站及定电压换流站外,其他换流站的注入功率保持不变,故在直流线路故障电流对换流站注入功率的灵敏度求解中,仅需考虑功率变化站和定压电压站对灵敏度数值的影响。 图4为柔性直流电网的等值电路,令定电压换流站为节点1;短路故障点在为节点m和节点m+1之间。 图4 柔性直流电网的等值电路Fig.4 Equivalent circuit of flexible DC power grid 图中ZΣ为环形直流电网线路总阻抗,Zmg为从节点m到故障点的直流线路阻抗。 (28) 根据电流分流定理,故障点两侧电流为: (29) 当换流站k的功率发生变化时,定电压换流站将调节功率,保持直流电网的功率平衡,即: -Δpcon1=Δpconk (30) 式中:pcon1为定电压换流站的注入功率;pconk为换流站k的注入功率。 综合式(27)、式(29)—(30)可得: (31) 式中ηk为t1时刻节点k的换流站注入功率对直流侧出口电流的灵敏度指标。 直流线路故障电流对换流站注入功率的灵敏度公式为: (32) 若柔性直流电网为3端网络,在定电压节点将环网打开,可得到等值两端网络的等值电路,如图5所示。图中P12、P′31为平衡节点向两端注入的有功功率,Z12、Z23、Z′31为直流线路阻抗,Pcon2、Pcon3为节点2、3的换流站注入功率,Z2、Z3分别为节点2、3与节点1′的总阻抗,Z′2、Z′3分别为节点2、3与节点1的总阻抗。 图5 两端网络的等值电路Fig.5 Equivalent circuit of two-terminal network 根据图5可得线路功率为: (33) 同理可推广到n端直流电网,可得节点m、m+1之间的功率为: (34) 当确定某一换流站注入功率变化,引起直流电网潮流波动,由式(32)和式(34)可得直流电网初始线路潮流与直流线路故障电流的关系。 (35) 上式表示柔性直流电网发生单极接地故障时直流线路故障电流对初始线路潮流的灵敏度指标。 首先通过MATLAB软件编写上述算法程序,然后在PSCAD软件上搭建了双端MMC-HVDC模型和四端MMC直流电网模型对理论计算结果进行仿真验证。模型参数来源于张北直流工程,如表1所示。由于半桥结构的MMC无故障阻断能力,通常直流线路会配置直流断路器以阻断故障电流,为防止换流器闭锁,直流断路器必须抢在换流器闭锁前动作,故本文仅对直流断路器动作前的6 ms暂态过程进行分析。 表1 张北四端柔性直流电网参数Tab.1 Parameters of Zhangbei four-terminal flexible DC power grid 将忽略交流影响的直流故障电流计算和本文计及交流影响的直流故障电流计算结果进行对比分析,如图6所示,详细计算过程及结果在附录A中给出。 图6 直流单极接地故障时直流电容电压和直流故障电流图Fig.6 Diagram of DC capacitor voltage and DC fault current during DC monopolar ground fault 由图6可知,忽略交流影响的直流放电电压与计及交流影响的直流放电电压相差20.20 kV,占换流站额定电压的4.04%;忽略交流影响的直流放电电压与计及交流影响的直流放电电流相差547.8 A,占直流故障电流的8.16%。而计及交流影响的电压、电流曲线与仿真曲线吻合度更高。因此,直流侧发生短路故障时,交流馈入对故障电流有一定影响,一旦忽略,将不利于对直流电网设备选型和控制参数整定。文献[15]考虑交流影响的直流故障电流计算方法考虑了控制方式对直流故障电流的影响,证明了控制方式对故障电流影响较小,因此本文建立的计及交流的直流放电等效模型中,忽略了控制方式的影响,保证计算精度的前提下,大大降低了计算复杂程度,同时得到了故障电流的具体解析表达式(而非递推公式[15]),有利于后续量化分析换流器注入功率及直流电网潮流变化对直流线路故障电流的影响。 将表1张北换流站参数代入式(27)中得到故障后6 ms,换流站注入功率对直流故障电流的灵敏度值,即: (36) 即初始有功功率每变化10 MW,故障后6 ms的直流故障电流将变化12.10 A,其变化量占额定电流约0.4%。图7为双端柔性直流系统发生单极接地故障后的直流线路故障电流图,可看出换流站注入功率和直流出口故障电流近似成线性关系,换流站注入功率越大对故障电流贡献越大。同时,与文献[21]得到相同结论,即整流站的交流系统对故障电流有促进作用(灵敏度值为正),逆变站的交流系统对故障电流有抑制作用(灵敏度值为负)。 图7 不同换流站注入功率下的直流故障电流Fig.7 DC fault current at different injection power of converter station 以张北四端柔直电网工程实例进行验证。丰宁换流站设为定直流电压控制方式,北京、张北、康保换流站设为定有功功率/定无功功率控制。线路参数为张北—康保49.2 km,康保—丰宁204 km,丰宁—北京190.4 km,张北—北京214.9 km。其他参数见表1。 设丰宁站为1号节点,北京站、张北站、康保站分别为2、3、4号节点,如图8所示。 图8 张北四端柔直电网拓扑图Fig.8 Topology diagram of Zhangbei four-terminal flexible DC grid 令故障点D1在张北站与康保站线路中点时,由式(28)和式(34)可求得: (37) (38) 线路参数决定着Z2、Z3、Z4和ZΣ的大小;故障点的位置影响着Z1g、Z2g、Z3g和Z4g的大小。令故障点D2在北京站、张北站线路中点时,同理可求。线路阻抗参数为0.009 95 Ω/km,线路等效阻抗参数计算结果如表2所示。 表2 发生故障时线路等效阻抗参数Tab.2 Equivalent impedance parameter of line in case of fault 由式(35)可知,k节点换流站注入功率发生变化时,在D1和D2点发生故障时(t=6 ms),直流线路的故障电流对初始线路潮流的灵敏度指标如表3所示。图9为张北四端模型D1点发生单极接地故障,通过改变张北站注入功率,分别设定为1 000 MW、800 MW、600 MW(对应状态1、2、3),得到不同初始线路潮流的状态下的直流线路故障电流的波形图,表4为图中波形的详细数据。 表3 直流线路故障电流对初始线路潮流的灵敏度指标Tab.3 Sensitivity index of DC line fault current to the initial power flow 图9 不同初始线路潮流状态下直流线路故障电流图Fig.9 Diagram of DC line fault current under different initial power flow states 表4 直流线路故障电流波形参数Tab.4 Waveform parameters of DC line fault current P34(t0)为初始线路传输功率;i34(t0)为故障初始时刻的线路电流值;i34(t1)为故障发生后(t0=2.006 s)的线路电流值;直流线路故障电流对初始线路潮流的灵敏度值∂i3g/∂p34分别为-1.820和-1.823,与计算值-1.835比较接近,误差仅占额定电流的1.5%,验证了本文方法有效性。当换流站3注入功率发生变化而引起直流电网线路潮流波动时,直流线路故障电流皆反向变化。原因是由于直流侧故障电流对换流站1(定电压站)注入功率的灵敏度值比较高,当换流站3注入功率增加,换流站1调节系统功率平衡,注入功率随之降低,进而导致直流线路故障电流降低,变化幅值则受线路参数和故障点位置的影响。其误差产生的原因主要是由于解析计算中受控直流电流源的等效和忽略换流器控制参数等影响因素。 本文提出了一种考虑交流馈入和稳态运行条件的柔性直流电网故障电流分析方法,并以实际工程为例通过仿真分析验证了方法的有效性。本文主要结论如下。 1)建立了计及交流馈入的直流放电等效电路数学模型,同时对模型中交流侧电流源进行等效。分析表明,直流侧发生短路故障时,若直流故障电流计算时不计交流馈入的作用,将影响直流电网设备选型和控制参数整定的准确性。 2)利用灵敏度分析的方法,得出换流站注入功率与直流侧故障电流成线性关系,换流站注入功率越大,直流侧出口故障电流越大。以张北站为例,换流站注入功率每变化10 MW,6 ms时对直流侧故障电流变化量占换流器额定电流的百分数约0.4%左右。 3)对于含有网孔的柔性直流电网,基于上述短路电流分析计算方法,通过潮流的负荷距法和线路分流定理得出了直流线路故障电流对初始线路潮流的灵敏度表达式,将初始线路潮流对柔性直流电网线路故障电流的影响进行了定性和定量的分析,进一步验证了原理和方法的适应性。本文所提直流短路电流计算方法可为柔性直流电网设备选型和参数整定提供必要的依据和参考。 由于目前实际的直流电网示范工程换流站基本未满载运行,新能源接入容量有限,故本文所考虑的场景中换流站功率波动不大,因此直流电网潮流在小范围内变化对直流故障电流的影响幅度亦有限。然而,随着新能源接入直流电网容量的进一步提升,其波动性和不确定性极易导致交流馈入功率以及直流潮流大范围内波动,所引起的直流故障电流变化将不容忽视,如考虑风电、光伏大规模脱网或并网工况。当然,此时应合理结合电源和直流电网各自的故障穿越策略,再深入讨论本文方法的适应性,这也是作者目前正在开展的研究课题。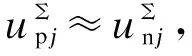
2 MMC-HVDC直流故障电流对换流站注入功率的灵敏度分析
3 故障前稳态潮流波动对直流线路故障电流的影响

4 仿真验证

4.1 MMC-HVDC交流馈入对故障电流的影响

4.2 直流电网初始线路潮流对直流线路故障电流的影响

5 结论
