产品网络的双曲结构

张忠元, 齐 霁, 齐 雯

(1.中央财经大学 统计与数学学院，北京 102206; 2.中央财经大学 金融学院，北京 102206)

随着企业的生产链遍布世界，跨国贸易一体化程度增大，全球性的产业内分工网络已基本形成.从国家的政策走向来看，我国当前经济发展的重点主要是产业升级与结构调整，尽管转型目标已经非常明确，但是仍然面临着升级方向选择、幅度调整和中断风险规避三大问题[1].传统的产业升级理论由于对产品网络空间所施加的连续性和同质性等极强假设，一定程度上缺乏对现实的解释力，并不能解决上述问题.对此，Hausmann和Klinger(2007)[2]从产出和能力视角创造性地提出全球产品网络(the Product Network)与比较优势演化理论，研究一个国家或者企业如何通过跨越产品之间的技术距离，实现生产能力禀赋向网络核心区域的跃迁.作为复杂网络科学应用于经济学领域的创造性成果，我国当前对这一理论的研究还处于援引和介绍阶段，对其涉及的深层次结构问题缺乏进一步研究.本文正是对此进行的一种尝试，即通过将复杂网络在几何结构方面的前沿研究——双曲空间理论，应用到全球产品网络中，探索产品网络是否能嵌入双曲空间中以及其嵌入结果的经济学解释.

双曲空间理论是将欧氏空间中的复杂网络拓扑结构嵌入曲率为负常数的双曲空间中，能够以更低维的度量空间对网络结构进行表征[3].双曲空间模型目前已经成功应用到社交网络、信息网络、文献网络和生物网络中，但和经济领域的复杂网络结合比较少.为了回答“产品网络是否具有双曲结构”这一问题，需要对产品网络进行准确的嵌入表示.一方面，选择合适的“双曲模型”对产品网络进行嵌入.常见的“双曲映射模型”有洛伦兹模型(Lorentz model)[4]、庞加莱圆盘模型[5]等.本文选择庞加莱圆盘，并使用Hydra[6]和Mercator[7]两个双曲算法进行嵌入.另一方面，本文选择另外两个非双曲的网络表示算法进行对比分析，即多维尺度变换MDS[8]和基于度校正的随机图模型dSBM[9].为了评价不同算法的嵌入质量，分别使用“Stress”和“AUPR”两个指标衡量嵌入效果.结果表示，双曲空间模型对产品网络的嵌入效果最佳，验证了其是一个双曲结构的猜想.进一步地，为了揭示产品网络在双曲空间中的分布具有经济学意义，通过方差分析(ANOVA)产品节点的径向坐标和产品质量、角度坐标和产品类别之间的相关性.计算结果的P值均显著，再次检验了“产品网络是双曲结构”的假设.

本文余下结构安排如下：第一部分介绍产品网络的构建过程和结构分析，第二部分对产品网络进行潜在几何分析和网络嵌入表示，第三部分给出了产品网络嵌入结果的经济学解释，最后是研究结论与总结.

1 产品网络构建和结构分析

本文参考Hidalgo等人(2007)[10]的研究，基于以结果为导向的度量方法构建全球产品网络，即以产品的“出口结果”代替产品的“生产过程”，这种计算方法不仅数据可得，而且有更严格的市场检验基础[11].进一步提出假设：如果越多的国家可以同时出口某两种商品，则认为这两种产品越具有相似的生产过程、生产能力，那么在两者之间进行升级的“跳跃距离”越小.换言之，产品能力越相似，企业在老产品上积累的知识和资源越能用于新产品的生产，越容易进行产品的升级，由此获得更高的经济收益[12].以“产品密度”描述产品之间的能力相似程度，以此构建产品相关矩阵和产品网络：

ρi,j=min{P(RCAxi|RCAxj),P(RCAxj|RCAxi)}.

(1)

其中，P(X|Y)为出口商品i的同时出口商品j的条件概率，RCA为显示比较优势(Revealed Comparative Advantage)：

(2)

其中，x(c,i)表示国家c关于产品i的出口额.如果RCA>1，则认为国家出口该产品的份额超过了全球出口该产品的份额.由此可对各国的出口产品进行限制，即只有当某产品的RCA>1时，国家才会出口该产品，反之则为无效出口.

本文构建产品网络的数据来源于Feenstra等人(2005)[13]和National Bureau of Economic Research(NBER)统计整理的1991—2000年国际贸易数据，其根据国际贸易标准分类(SITC)四位码对产品进行分类，如表1.参考马海燕和于孟雨(2018)[11]的数据处理方法，按照如下步骤进行数据清洗：①剔除未始终存在于数据集中的国家和产品；②剔除商品编码尾数为“A”和“X”序号不清楚的商品.最终形成包含141个国家1 288种商品的10 a国际贸易数据集.

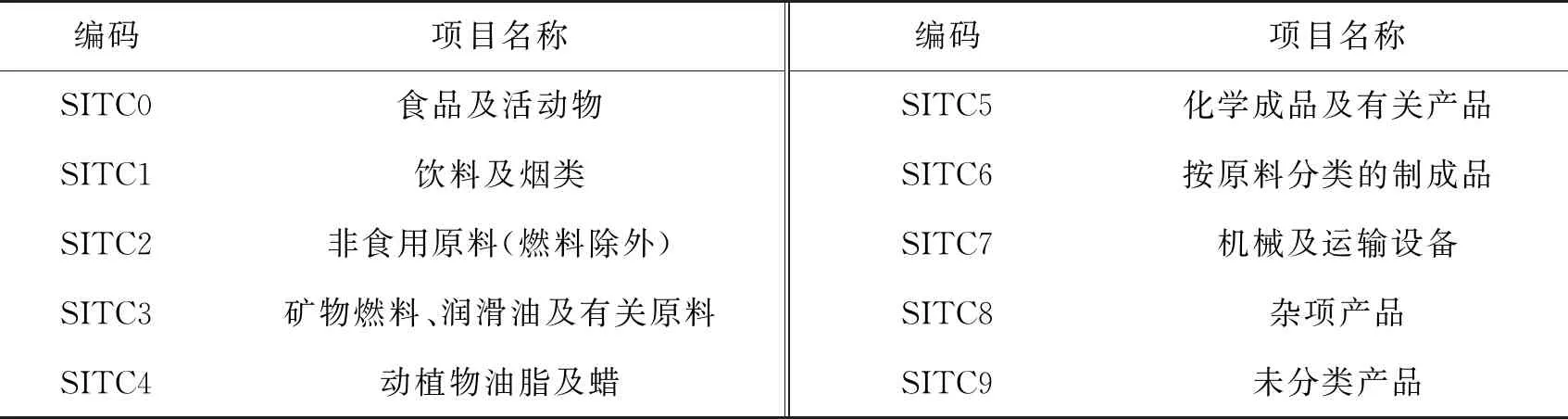
表1 国际贸易标准分类

利用上述数据，根据公式(1)和公式(2)构建了1 288×1 288的产品邻接矩阵.矩阵中每一行、列各代表一种产品，每一非对角线元素表示一对产品间的“能力相似度”.图1(左)为产品相关矩阵的热图，图1(右)为经过平均联动层次聚类的相关矩阵热图，在一定程度上揭示产品网络存在相似产品聚集的社团结构.另外，可发现图中存在许多空行、空列，表明有部分产品不是任何一个国家的有效出口商品(RCA<1)，最终能够有效出口的产品数只有769种，构成769×769的有效产品网络.

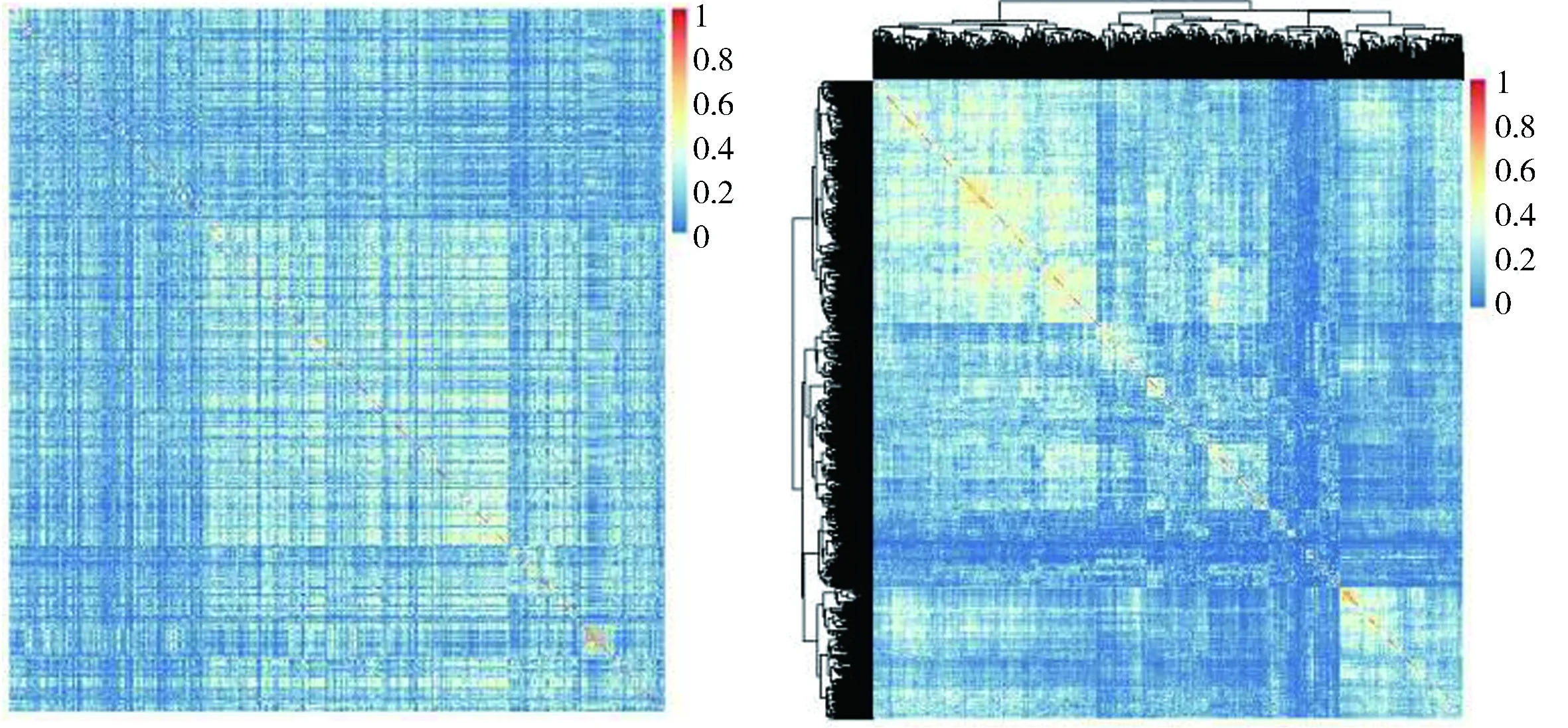
图1 2000年产品相关矩阵热图(右图经过层次聚类处理)

2 产品空间网络结构分析

根据产品相关矩阵可以构建产品网络，其节点为每一个产品，边为产品之间的“能力距离”.图2(A)的图中图为产品网络及其网络密度ρ(Network Density)随时间的变化情况.由于大部分产品为有效出口商品，所生成的产品网络比较稠密但随时间略有下降(ρ1991=0.87，ρ2000=0.58).但图2(A)中的连边权重呈现高度左偏分布，即大多数连边的权重都非常小，表明多数产品之间的相似性非常小.这也侧面反映了产品网络中可能存在一些强连接、稀疏的“网络骨架”，这代表了产品潜在升级的主要方向.为了提取产品网络中更显著的连边信息，抽取产品空间的“p%-网络骨架”进行分析.将产品相似性降序排列后计算前p%分位数(p=10,20,25)，以此构建10%、20%和25%的网络骨架.图2(B)展示了1991—2000年间产品网络的“10%”网络骨架的累计度分布，嵌入子图为其局部聚类系数随节点度的变化情况.结果发现，产品节点的度值呈幂律分布，表现出无标度网络的特征(拟合优度R2=0.833 8).

图2 网络密度和连边权重(A)、累计度分布和局部聚类系数(B)

3 产品空间网络潜在几何分析和网络嵌入

双曲几何(Hyperbolic Geometry)是非欧几何的重要分支，可以描述为曲率为负常数的空间上的几何学，而更熟悉的欧氏几何则是“平直”空间上的几何，即空间曲率为0的欧氏空间.两种几何学最基本的区别在于“平行公设”不同，即在双曲空间中过直线外一点有无数条直线与之平行，而欧氏空间中有且只有一条平行线.从直观上看，双曲空间比欧氏空间“容积更大”“增长更快”，因此，一个只能嵌入高维欧氏空间中的网络拓扑，可以很简单地映射到一个低维的双曲空间中[14].

为了更方便地描述双曲空间，提出了多个映射到欧氏空间中的双曲模型，如洛伦兹模型、庞加莱圆盘模型等.每个模型代表双曲几何不同方面的性质，其中,最常用的是庞加莱圆盘模型.其将双曲平面2映射在一个二维欧氏空间2中的单位圆中，即其中，z1=tanh(r/2)cosθ和z2=tanh(r/2)sinθ是双曲极坐标，可通过对双曲平面中的点x=(x0,x1,x2)进行球极投影(Stereographic Projection)得到，如式(3)：

(3)

由此可以求得双曲平面上两点之间的双曲距离：

d((r1,θ1),(r2,θ2))=arcosh(coshr1coshr2-sinhr1sinhr2cos(θ1-θ2))，

(4)

且双曲空间中的直线可用欧氏圆盘上的弧长表示.

为了揭示产品空间网络的隐藏几何结构，本文采取4种网络表示方法对产品空间及其“p%-网络骨架”进行低维空间嵌入或表示，分别为二维欧氏空间2嵌入算法多维尺度变换(Multidimensional Scaling，MDS)[8]、二维双曲空间2嵌入算法的Hydra[6]和Mercator算法[7]，以及非几何的网络表示方法的基于度校正的随机图模型dSBM[9].

4种算法中，MDS和Hydra两个算法的原理相似，即保障原始空间和低维嵌入空间中的样本间距离尽可能一致.目标函数如式(5)：

(5)

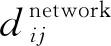
Mercator算法同样可以将网络嵌入双曲空间中并为节点找到合适的坐标，但与Hydra的原理不同，其是一种基于连接关系而忽略连接权重的算法，并将最大似然估计法和机器学习结合，更高效地推断双曲几何“流行度-相似度”模型中的节点潜在坐标，详情见文献[7]. 除了将网络嵌入某一几何空间中进行表示以外，还可以通过推断网络中的社团结构和连接概率对网络进行表示，如基于度校正的随机区块模型(dSBM)，也是基于网络连接关系的算法.注意，Mercator和dSBM两种方法只适用于对网络的“p%-网络骨架”进行表示.

对于完整的产品空间网络的嵌入结果，本文根据式(5)计算Stress值作为衡量网络嵌入质量的评价指标，Stress值越小表明嵌入结果越好.针对网络骨架的嵌入结果，首先,基于4种算法的嵌入结果反过来对网络进行重构，即预测两节点之间的连边是否存在，因而可建立一个二分类任务;其次，对于此分类学习，通过计算AUPR(Precision-Recall曲线下面积)[15]来评价4个“分类器”的预测性能，AUPR越接近1表明其预测效果越好.

将1991—2000年10 a的产品空间的完整网络、25%、20%和10%的网络骨架进行嵌入和表示(图3).其中，图A为完整的产品空间网络进行Hydra和MDS嵌入的Stress值，图B为4种算法分别对产品空间的“25%-网络骨架”进行网络重构的AUPR值，其他网络骨架的嵌入结果类似.可知，基于双曲几何的网络嵌入算法Mercator的AUPR值始终最高，即其对网络的重构效果最好，且与网络骨架的提取程度无关.第二个双曲嵌入算法Hydra算法表现也较好，无论是针对完整的产品网络(Hydra的Stress值 < MDS的Stress值)，还是任意的网络骨架的嵌入，都大幅超过了MDS和dSBM两种非双曲的网络表示算法.欧氏空间的网络嵌入算法MDS和非几何表示算法dSBM表现均较差.

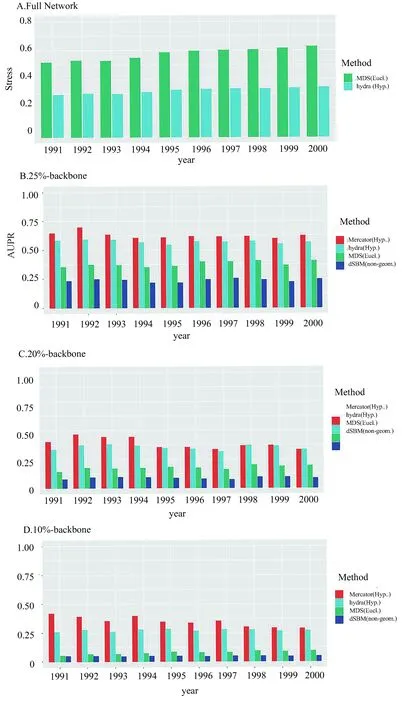
图3 产品空间网络嵌入结果评价：Stress和AUPR

总的来说，可以观察到产品空间网络潜在度量空间，更适合用曲率为负的双曲几何而非曲率为0的欧氏几何表示.此外，双曲空间在网络重构的质量方面甚至优于非几何的随机图模型.

4 双曲产品空间的经济学解释

Papadopoulos等人(2012)[16]的“流行度-相似度”模型和Serrano等人的1模型[17]，可用来直接解释庞加莱盘中潜在的双曲网络坐标的意义：径向坐标r代表节点的“流行度”，角度坐标θ代表节点的“相似度”.另外,Hydra嵌入算法给出了将r解释为流行度、将θ解释为相似度的理论基础.因此，在产品网络的背景下，提出两个假设证明双曲坐标的经济可解释性：假定一个给定产品的流行度与其产品质量一致，且在双曲空间中的分布与产品的类别划分有关：(H1)产品质量与产品在双曲空间中的径向坐标分布相关；(H2)产品类别与产品在双曲空间中的角度坐标分布相关.

为了验证第一个假设H1，即产品网络的双曲径向坐标与产品的质量有关，本文根据Lall(2000)[18]的研究对产品质量进行划分，共分成5大类：初级产品(PP)、资源型产品(RB)、低技术产品(LT)、中技术产品(MT)和高技术产品(HT).通过ANOVA检验，可以发现节点的径坐标与产品质量之间始终存在显著的相关性，无论是Hydra还是Mercator的P值均小于0.000 1.进一步地，通过产品网络的双曲空间可视化也同样验证了假设1(图4)，其描述了1991年、1994年、1997年和2000年产品网络的Mercator双曲嵌入结果，由此可以看到一个全球产品分布的发展历程.产品空间网络表现出异质性和一个“核心-边缘”结构：网络的核心由金属产品、机械产品和化学品等高、中技术产品(HT、LT)组成，而外围则由农林牧矿等初级产品(PP)或低技术产品(LT)组成.随着世界各产品的贸易量逐渐扩大(用节点的大小表示)，初级产品(PP)和资源型产品(RB)最初在产品空间的“森林”中位于边缘地带，逐渐“移居”到了核心地带，但高技术产品(HT)则逐渐扩散到边缘，但这并不表明其重要性的下降，相反高新技术产品的逐渐聚集成团(图4第4张图的右下角部分).这在一定程度上表明，在全球分工“一体化”背景下，大量低端制造业或低级产品的生产逐渐从发达国家转移到发展中国家，从而加强了这类产品的全球关联性.但发达国家所掌握核心高端技术在全球的辐射扩散程度减小同时垄断现象加强，由此促使全球产品网络形成图示的分布现象.

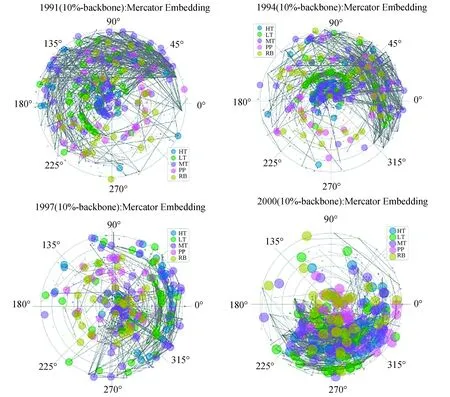
图4 产品空间网络双曲嵌入结果(Mercator嵌入：1991年、1994年、1997年和2000年)

根据假设二，认为产品空间网络在双曲空间中将按照产品类别表现出角度的聚集现象，即产品类别会影响产品节点在双曲空间中角坐标的分布.按照国家贸易标准SITC4可将产品分成10大类(表1).因此，根据同样的思路，本文采用适用于圆形数据(Circular Data)的ANOVA检验[19]，验证每一类产品在双曲空间中的角坐标是否存在显著差异.

(6)

结果表明，在1991—2000年期间，角坐标θ和产品类别之间存在显著联系(Hydra和Mercator两种方法的P值 <0.000 1).这表明，产品空间网络的边缘社团结构(非网络核心的部分)确实与产品的类别划分保持一致，验证了假设H2.

5 研究结论

本文基于国际贸易标准SITC4的1991—2000年产品贸易数据，结合显示比较优势RCA指标，构建了全球141个国家769×769的产品空间网络，并明确检验了其潜在度量空间可以很好地用负曲率的双曲几何表示.通过将产品网络嵌入庞加莱圆盘中对网络进行可视化，并根据Papadopoulos等(2012)的“流行度-相似度”模型思想和ANOVA分析方法，发现产品网络中产品节点的径坐标(“流行度”)和产品质量高度相关，角坐标(“相似度”)则与产品的SITC4分类标准显著关联.从时序角度看，发现低端制造业或低级产品的全球关联性加强，高端技术产品则扩散程度减小同时垄断现象加强，促使全球产业格局发生明显变化.