基于改进欧几里得聚类的激光雷达障碍物检测
2021-10-15葛平淑崔芳磊周宏宇
张 阳,葛平淑,崔芳磊,周宏宇,张 涛
(大连民族大学 机电工程学院,辽宁 大连 116605)
障碍物检测技术作为智能车辆和汽车辅助安全驾驶系统中的一项重要感知技术,其检测精度的高低直接影响行车的安全。智能汽车的障碍物检测根据传感器类型主要分为两类:基于机器视觉的障碍物检测和基于激光雷达的障碍物检测。基于机器视觉的障碍物检测成本较低,算法比较成熟,但易受光照的影响,在一些条件下检测精度较低,不能实现全天候准确检测。激光雷达拥有检测范围广、精度高、抗干扰能力强等优点,如今已经被广泛应用于障碍物检测领域[1]。
基于激光雷达的障碍物检测方法主要有以下三种:基于密度的聚类算法(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)、K-means聚类算法和欧几里得聚类算法(Euclidean)[2]。DBSCAN聚类是比较具有代表性的基于密度的聚类算法,可以检测出任意形状的簇并识别噪声点,但点云的密度会影响聚类效果,并且该方法对内存的占用较大,如果点云数量较多会对处理器的性能提出更高的要求[3]。K-means算法原理简单,速度快,聚类效果较好,但需要事先确定聚类的数目K,在复杂的交通环境中难以提前确定K值。欧氏聚类对于点云数据具有很好的分割效果,但需要输入一个固定的距离阈值。由于激光雷达点云具有近处密集远处稀疏的特点,该方法在对点云进行障碍物检测时检测精度较低[4]。本文对传统欧氏聚类进行改进,利用距离阈值动态选择代替固定阈值,能有效改善传统欧氏聚类由于点云密度不均导致的检测精度不高的问题。
1 欧氏聚类分割
1.1 确定距离阈值
欧氏聚类即基于欧氏距离的聚类算法,针对点云中的n个点,需要确定一个欧氏距离d,使小于d的点合并为一类,并且经过多次迭代合并同时计算剩余类之间的欧氏距离,直到所有类之间的欧氏距离都大于d,则聚类结束[5]。包含m个点的第i类和第j类之间的欧氏距离:
(1)
1.2 近邻搜索算法
由于激光雷达点云数据量过大,以64线激光雷达为例,一帧点云图中包含的点数在十万以上,并且点云的分布不均,导致了算法搜索目标点很难有较高的效率。在辅助安全驾驶系统以及无人车当中,障碍物检测需要在较短的时间内完成。为了提高算法的实时性,需要在离散的点云之间建立一定的拓扑关系,从而对领域中的点或集群实现高速查找。在离散的点云之间建立拓扑关系主要有两种方法:Octree(八叉树)和KD-Tree[6]。
Octree是一种描述三维空间的树状数据结构,每个节点都表示一个正方体的体素,每个节点可以分为八个子节点。Octree通过对三维空间中的实体进行体元剖分,可以使每个体元都具有相同的时间和空间复杂度,从而得到一个具有根节点的方向图。Octree的每一个叶子节点都由相同属性的体素构成,如果属性不同则需要进一步拆分,直到叶子结点中只存在相同属性的体素[7]。Octree的原理如图1。

图1 Octree原理
KD-Tree相当于二叉树的多维扩展,每个非叶子结点可以看做一个超平面,将空间分为两个子空间,实现对多维数据的组织和存储。如果叶子结点的数目达到了设定的阈值,则不再进行划分,否则继续划分叶子结点。为能够处理三维点云数据,需要建立三维KD-Tree[8]。KD-Tree的算法流程如图2。

图2 KD-Tree流程图
为对比两种邻域搜索方法的效率,对同一帧点云构建拓扑关系。当点云数据量较少时两种方法拥有相似的效率。当数据量增大,每个点附近点增多,KD-Tree在离散点之间建立拓扑关系花费的时间更少,由于激光雷达点云数据量非常大,同时对实时性也有很高的要求,故本文选择KD-Tree对点云进行邻域搜索。
1.3 改进欧氏聚类算法
传统的欧氏聚类算法适合密度均匀的点云数据,对于密度不均的点云数据处理效果不理想。为了对不均匀的点云数据进行处理,各国的学者提出了很多种方法。Francisco de A.T.等[9]提出了一种自适应阈值的聚类算法,可以根据障碍物的形状和大小动态设定阈值,但该方法只适用于点云数目和待测目标均较少的情况,车载激光雷达扫描得到的数据量较大,判断所有障碍物的形状和大小需要花费较长时间,算法的实时性不好。刘畅等[10]以到激光雷达的距离为半径划分区域,不同的区域选择不同的距离阈值,但该方法需要预先将点云按照半径分割,有可能在分割的过程中将一个障碍物分割为两个从而造成误检。本文针对点云密度不均的问题提出了动态选择距离阈值的欧氏聚类算法,根据点到激光雷达的距离变化更改距离阈值的大小。
算法共分为四步:
(1)通过KD-Tree建立点云cloud中离散点之间的拓扑关系;
(2)初始化一个过渡聚类队列nn_indices、一个种子队列seed_queue、一个空的聚类列表clusterIndices,并将cloud中每一个点ci加入到seed_queue中;
(3)针对seed_queue中的第i个点ci,搜索半径r小于距离阈值d内的邻域,将搜索到的点全部存放在nn_indices中,计算nn_indices中每一个点到ci的欧氏距离,将距离最小的点划分到同一类中,并将得到的聚类存放在clusterIndices中,迭代循环多次,直到处理完seed_queue中的每一个点,每次循环都刷新nn_indices;
(4)计算clusterIndices中每一个聚类到其他聚类之间的欧氏距离,将欧氏距离最小的聚类合并为同一个聚类,经过多次迭代循环,直到每一个聚类到其他聚类之间的欧氏距离都大于d为止。d是关于数据点坐标的表达式:
(2)
式中:Xi和Yi是待搜索的点或待搜索的聚类中心点的坐标;α和β是用来调整d的参数,与激光雷达的角分辨率和角度精度有关,角分辨率越小,角度精度越高,α和β的值越小,具体数值需通过多次实验确定。
2 实验验证
实验软件环境为Windows10,编程语言为C++,以随机抽取的一张点云图为例,通过处理点云图观察实验结果完成对算法的验证。
在对点云图进行聚类之前需要进行预处理,由于激光雷达点云数量较大,直接处理会占用大量的内存,算法运行速度缓慢,不符合实时性的要求。所以需要先减少点云的数量,将实验中没有作用的点去除,提高算法速度的同时避免误检。预处理包括设置感兴趣区域、下采样、使用RANSCA去除地面点,可以有效减少点云数量的同时较好地保存障碍物点的特征。原始点云图如图3。

图3 原始点云图
由于杆之间距离较近,在侧向容易将两个杆误看成一个,为方便观察,预处理后的点云图如图4。

a)侧视图 b)俯视图
本文任选十张预处理后的点云图,共包含110个障碍物,分别使用改进欧氏聚类算法和传统欧氏聚类算法进行聚类,对比两种方法的准确率。通过多次实验找到传统欧氏聚类的最佳距离阈值,准确检测到障碍物100个,准确率为90.9%,准确聚类的数量变化如图5。

图5 准确聚类的数量变化
在传统欧氏聚类的基础上获取改进欧氏聚类的距离阈值,经过多次实验使所有点云图中距原点5 m以内的障碍物得到准确聚类,得到距离阈值d1,再使距原点25 m到30 m内的障碍物得到准确聚类,得到距离阈值d2。距原点5 m以内的障碍物共25个,距原点25 m到30 m内的障碍物共30个,准确聚类的数量变化分别如图6和图7。

图6 距原点5 m以内准确聚类的数量变化
将d1、d2及对应的距原点距离带入式2中,经过调整得到动态距离阈值d,准确检测到的障碍物有107个,准确率为97.3%。由此可见改进欧氏聚类算法相比传统欧氏聚类算法有明显的提升。
采用传统欧氏聚类算法聚类后的结果如图8,限制聚类的最小点数为10。可以看出对于距离激光雷达较近的障碍物聚类效果较好,但将雷达后方的车辆分成了两个聚类。这是因为距离阈值选择较小,车辆障碍物点云内部间距大于距离阈值。
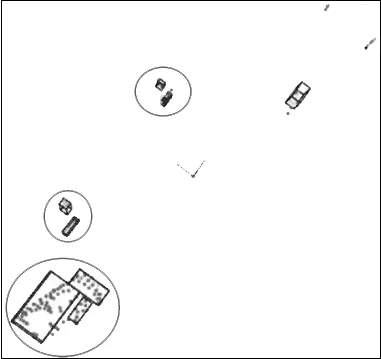
图8 传统欧氏聚类结果
为了解决这一问题增加距离阈值,聚类结果如图9。可以看出距离激光雷达较远的障碍物聚类效果较好,但将激光雷达后方的两根电线杆聚成了一类。可以看出传统欧氏聚类算法具有一定的局限性,难以同时对近处和远处的障碍物进行准确聚类。

图9 传统欧氏聚类结果2
改进后的欧氏聚类算法聚类后的结果如图10,经过多次实验对α和β进行调整,可以看出对于近处和远处的障碍物都有较好的聚类效果,算法的抗干扰能力有了一定的提高,没有发生误检。

图10 改进欧氏聚类结果
3 结 语
针对传统欧氏聚类算法在对分布不均的点云进行处理时存在的弊端,本文提出了一种改进欧氏聚类算法,能够将距离阈值与障碍物点到激光雷达的距离关联起来,通过动态选择距离阈值,解决了传统欧氏聚类算法的弊端,可以对不同距离的障碍物实现准确检测。后续将在障碍物检测的基础上完成对障碍物的识别工作。
