正交三极化MIMO系统有益入射角谱分布的研究

戴勇 李伟 汪大洋 赵金城 海凛

【摘要】    基于相关矩阵研究入射波角度扩展对多极化MIMO系统性能的影响。发现使用三个正交极化天线元的MIMO系统在采用一定的入射波角谱分布时，能够使相关矩阵中特定元素的值增加，这种增加对系统容量有提升作用。通过建模对提升关键相关性系数的条件进行分析，得到能获得更高信道容量的散射体角度扩展。

【关键词】    MIMO    多极化    相关系数    信道容量

引言：

关于MIMO系统的研究已经非常广泛，通常采用EDOF[1]、相关矩阵秩[2]、信道矩阵乘以其共轭转置的特征值[3]等标准对系统性能进行衡量。但EDOF和特征值都是一系列随机数值，对系统性能的描述并不直观;而相关矩阵是一个有着确切数值的矩阵，且对相关矩阵各元素的功能已经有了较深入的分析，可以更加直观地看出其对系统性能的影响。

一般来说，天线分集的目标就是降低子信道之间的相关性，从而提升系统容量。但相关系数实际上可以分成交叉相关系数和收发相关系数两类[4-5]，其数值的降低对系统容量分别起到增加和降低的作用。因此，在本文的研究中倾向于选择以相关性系数作为标准进行衡量，得到各类相关系数的具体数值，就能够对系统的大致性能进行评估。

在过去以相关系数作为衡量标准的研究中，常采用Kronecker积方法[6-7]，利用收发相关矩阵近似获取整个相关矩阵。但该矩阵中所有的交叉相关系数恰好均是通过近似计算获得，这就导致无法精确对系统的真实性能进行分析。而我们在采用非Kronecker积建模方法进行研究的时候，发现正交三极化MIMO系统在某些散射体分布的情况下可以实现交叉相关系数的提升，从而使得系统性能有所增加。本文对这一情况的实现过程和原理进行详细分析。

一、信道模型获取相关系数

1.1 MIMO系统的物理模型

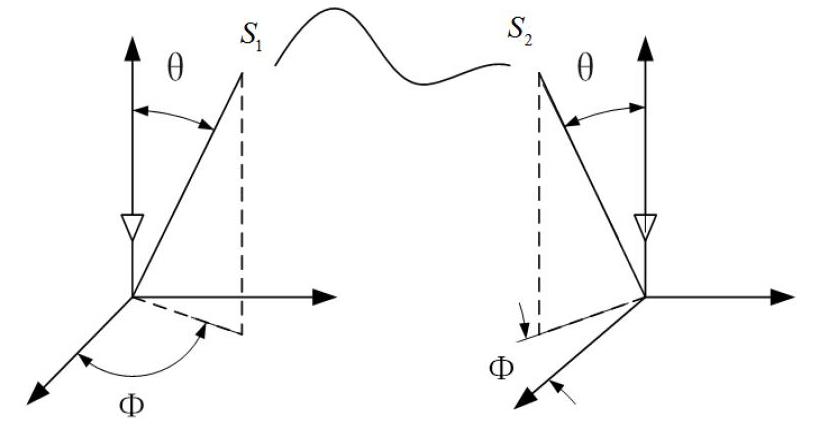
对MIMO系统相关性的计算，一般通过对接收信号在散射体扩展角度范围内进行积分获取。然而[6-7]等采用的模型仅能描述发射天线之间的相关性或接收天线之间的相关性，所以必须采用Kronecker积方法。为避免这种情况，我们选择了一种描述信号整个传播过程的信道模型[8]，其中MIMO系统的信号传播示意图如图1所示，对接收端来说，接收信号来自于方位面和俯仰面这一角度扩展内的散射体，其中和是方位面内的平均入射角和入射角度扩展范围，和分别为俯仰面内的平均入射角和入射角度扩展范围。Ω描述的是当前入射信号所在方向的立体角，简便起见假设散射体在ΔΩ内的分布密度为常数，在ΔΩ以外没有散射体存在。

为便于分析，我们采用和文献[8]中相同的设置，令散射体相对收发端所在的方向角一一对应，并且散射体相对发射端的分布与相对接收端的分布对称，如图1所示，其中发射信号从左边的坐标原点出发，到达散射体S1再经过S2，然后到达接收端。而S1相对发射端的所在位置，和S2相对接收端的相对位置完全对称。

以散射矩陣描述发射信号的电场经由Ω散射体后发生的变化，即

（1）

式中，，和为复高斯变量，其方差由XPD、CPR等环境参数决定。

正交三极化MIMO系统的天线编号1、2和3分别代表沿x、y和z轴极化的电流元天线。第k个天线元的方向图函数为，在和方向上的分量分别是和，则发射天线m到接收天线n之间的子信道响应为

（2）

子信道之间的相关性系数可以写成

（3）

其中

（4）

通过式（2）～式（4），我们就能够计算出任意入射角谱扩展下各子信道之间的相关系数。

1.2相关系数的计算

给定入射角分布，即和、和，则各子信道之间的相关系数计算举例如下：

（5）

通过这样的模型，可以将积分式完全转化为三角函数的四则运算，从而能够精确计算出所有的相关系数，然后组成完整的相关矩阵：

二、相关性与信道容量

2.1 MIMO系统的相关性研究

当时，我们任取和进行计算，例如，，精确计算得到的相关矩阵如下：

（6）

从上式可以看出，所有非零的相关系数即ρ11，22，ρ11，33，ρ21，12，ρ31，13，ρ22，33，ρ32，23均为交叉相关系数。

由于文献[4-5]指出，不同于传统的收发相关系数，交叉相关系数（即对应收发端均不使用同一根天线的子信道之间的相关系数）的增加反而会带来系统容量的提升。因此，在前述的条件下，也就是当散射体扩展角度对称时，系统容量必然有所提升，甚至能够超过所有子信道完全不相关的理想情况。而我们的研究目标变成：在何种角度扩展下，能够尽可能地使交叉相关系数的数值提升，从而获得尽可能高的系统容量。

2.2容量的计算

根据文献[9-10]，MIMO信道容量的上界与各种相关系数有着直接的关系，可以由下式描述2x2 MIMO系统的性能：

（7）

式中为容量影响因子，m为发射天线数量，Es /N0为信噪比，si为交叉相关系数，r和t为传统收发相关系数。这个式子基本描述了不同相关系数对信道容量的影响，我们将其推广到3x3或者更多收发天线的情况，得到：

（8）

对计算出的相关系数进行分析可以得到如下结论：在的情况下，收发相关系数即（8）式中rj和tj必然为零，且能够影响的交叉相关系数si有限。此时问题变为如何尽可能提升这几个相关系数的取值，以及在无法同时提升的情况下，如何使其平方和最大。

根据式（3）-式（5），我们可以绘制出入射角谱扩展与各相关系数平方的关系图，如图2所示。

圖2    相关系数平方随散射体分布的变化

从图2可以看出，ρ11，33和ρ31，13取值较小，受环境影响的变化幅度也比较小。而其余相关系数的变化明显，ρ22，33和ρ32，23在较小的时候取值变大，ρ21，12在较小的候取值变大，而ρ11，22在和都比较小的时候获得最大值。综合考虑以上情况，将利用式（7）进行计算，可以得到入射角谱扩展与容量影响因子的关系，如图3（a）所示。

从图3（a）可以看出，最高的信道容量上界在深红色区域获得，即很小的时候，或者和都在60°以下的时候。由于所有子信道互不相关的理想情况下容量影响因子为1，图中任一点的情况都可以获得比理想情况更优秀的系统性能。

此外，我们还可以利用解析模型以获得平均信道容量，因为MIMO解析模型可以通过已知的统计参数，即相关矩阵和各子信道的功率，产生出符合这些统计特征的随机信道响应。其结构如下：

（9）

其中Hw是所有元素独立同分布的随机矩阵，R为已知的相关矩阵。将前面计算出的相关矩阵代入解析模型，并将各子信道功率进行归一化，然后采用蒙特卡洛方法进行仿真，可以直观反映出入射角谱扩展与平均容量的关系，如图3（b）所示。

可以看出3（a）和图3（b）的结论有着高度的一致性，即入射角的，且很小或和都在60°以下的时候，可获得较高的平均信道容量，且比起所有子信道完全互不相关的理想情况下的平均容量（约为8.22 bit/s/Hz）有着明显提升。

三、结束语

本文在散射体相对收发端连线呈对称分布的情况下，分析了入射角谱扩展和相关矩阵的关系，得到了在一定入射角谱扩展的情况下，部分交叉相关系数可以得到有效增加，从而获得系统性能的提升。

目前对于非零和情况下的研究并没有得到足够的结论;另外过去的研究中虽然包括了含3个电流元和3个磁流元组成的全极化天线[6]，但本文中并没有考虑，因为相关矩阵极为庞大和复杂。下一步我们将会进行更深入的研究。

参  考  文  献

[1] L. Zhu， S. Wang and J. Zhu， “Adaptive Beamforming Design for Millimeter-Wave Line-of-Sight MIMO Channel，” in IEEE Communications Letters， vol. 23， no. 11， pp. 2095-2098， Nov. 2019.

[2] K. Honda and K. Ogawa， “Over-The-Air Apparatus for Large-Scale MIMO Antennas to Create the Full-Rank Channel Matrix，” 2020 International Symposium on Antennas and Propagation （ISAP）， 2021， pp. 547-548.

[3] D. Piao， “Characteristics of the Hexapolarized MIMO Channel over Free-Space and Three Non-Free-Space Scenarios，” in IEEE Transactions on Wireless Communications， vol. 12， no. 8， pp. 4174-4182， August 2013.

[4] S. M. Mikki and Y. M. M. Antar， “On Cross Correlation in Antenna Arrays With Applications to Spatial Diversity and MIMO Systems，” in IEEE Transactions on Antennas and Propagation， vol. 63， no. 4， pp. 1798-1810， April 2015.

[5]Clerckx B， Oestges C. MIMO wireless networks： channels， techniques and standards for multi-antenna， multi-user and multi-cell systems. 2nd ed. Amsterdam： Academic Press， 2013.

[6] T. Svantesson， M. A. Jensen and J. W. Wallace， “Analysis of electromagnetic field polarizations in multiantenna systems，” in IEEE Transactions on Wireless Communications， vol. 3， no. 2， pp. 641-646.

[7] C. A. Viteri-Mera and F. L. Teixeira， “Feasibility analysis of polarimetric-interference alignment beamforming in rich-scattering indoor channels，” 2016 IEEE International Symposium on Antennas and Propagation （APSURSI）， 2016， pp. 335-336.

[8] N. Prayongpun， K. Raoof， “Impact of depolarization phenomena on polarized MIMO channel performances，” I. J. Communications， Network and System Sciencesy， vol. 1， no.2， pp. 124-129， May. 2008.

[9]Oestges C， Paulraj A J， “Beneficial impact of channel correlations on MIMO capacity，” Electronics Letters， vol.40， no. 10， pp. 606-608， May 2004.

[10]C. Oestges， B. Clerckx， D. Vanhoenacker-Janvier and A. Paulraj， “Impact of diagonal correlations on MIMO capacity： application to geometrical scattering models，” 2003 IEEE 58th Vehicular Technology Conference. VTC 2003-Fall （IEEE Cat. No.03CH37484）， 2003， pp. 394-398 Vol.1.