基于波像差判据的同步相移显微干涉检焦方法

胡乔伟，高志山，袁 群，黄 旭，孙一峰，王灵杰，张建萍

（1.南京理工大学 电子工程与光电技术学院，江苏 南京 210094；2.中国科学院长春光学精密机械与物理研究所 光学系统先进制造技术重点实验室，吉林 长春 130033）

引言

激光直写技术是光刻母版衍射光学元件生产的重要工艺技术之一[1]。随着光刻工艺制造的要求不断提高，对于激光直写技术核心部件激光聚焦系统的写入精度有很高的要求[2]。为了提高精度，减小直写波长[3]和增大物镜的数值孔径[4]是2 个有效的方法。目前，激光直写波长已经从He-Cd 激光的442 nm[5]发展到了深紫外（deep ultraviolet，DUV）[6]的193 nm，而光刻物镜的数值孔径也从0.3[7]提高到0.8[8]。随着物镜NA的增大，物镜焦深也在不断变小[9]，并且随着微光学元件表面的尺寸扩大[10]和复杂度加深[11]，使得检焦变得更难。检焦光路负责将直写物镜焦点定位于曝光平面，指导直写波长下的聚焦激光束，在每一次直写前进行实时检焦及焦点调整。

目前的同轴检焦方法主要有像散法[12]和临界角法[13]等。2001年，美国亚利桑那州立大学的Fan K-C 等人提出了物镜数值孔径NA为0.45、检焦波长为780 nm 情况下的像散法自动检焦方法[14]。像散法是利用像散元件与四象限探测器对输出信号分析计算进行离焦的判断，对焦范围为200 μm，检测精度为0.2 μm，该方法对焦范围较大但检焦精度较低。2011年，长春光机所梁凤超等人提出了基于临界角法的激光直写调焦伺服技术，其NA为0.42、检焦波长为632.8 nm[15]。利用非临界角的光斑不均匀性与二象限探测器解析离焦量，其对焦范围为10 μm，检焦精度为80 nm。当前国内较为先进的257 nm 激光直写机对于检焦精度的要求在25 nm 以内。

现有方法虽能实现对离焦量的检测，但由于直写波长与检焦波长差异越来越大，对于物镜在不同工作波长下的像差校正难度越来越大。因此需要设计一种新的方法，减小由于物镜自身像差带来的检测误差问题；另一方面，干涉检测的灵敏度很高，将其用于检焦，可以实现纳米量级的检焦精度，现有检焦方法虽然对焦范围大，但检测精度较低，适用于粗调焦。因此，本文提出了一种基于波像差判据的同步相移显微干涉检焦方法，利用其波像差检测灵敏度高、同步相移实时性强等优点，将采集得到的同步相移干涉图解调出显微物镜的干涉波像差信息，再从大数值孔径（NA）的显微物镜波像差数据中解析出离焦量的大小与方向，可以实现高精度以及实时的焦面探测。

1 检焦原理

1.1 检焦工作原理

限于篇幅，本文仅聚焦检焦波长的检焦精度和方法讨论。同步相移显微干涉检焦系统，通过对显微物镜的光瞳波像差的探测与分析来实现离焦量的检测，在激光直写系统使用的物镜数值孔径为大数值孔径（NA）时，如测试臂中样品表面偏离物镜焦点时，则在波像差中不仅会引入离焦量，还会引入初级球差和高阶球差。

如图1所示，为离焦量S与波面关系的模型。当样品表面没有位于焦点O1时，此时参考点O2距离波面焦点O1有轴向偏移量S，即离焦量S，分别将O2与P之间的距离和O1与P之间的距离记作O2P与O1P，则两点之间光程差可以表示为

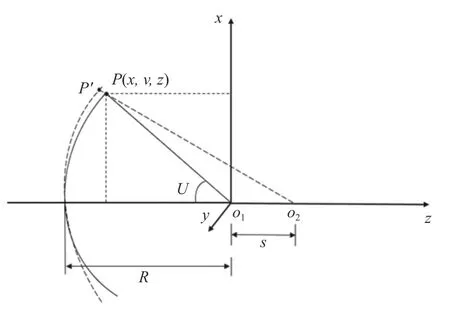
图1 离焦量S 与波面关系模型示意图Fig.1 Schematic diagram of relationship model between defocusing amount S and wave surface

由于离焦量S相较于R较小，所以S2/R2可以忽略不计，则波像差可以化为

式中：U为考察点的孔径角，其与整个口径球面波的NA之间的关系可表示为

式中，ρ为归一化波面极坐标。

结合（2）式和（3）式可以得到，待测元件离焦所引入的波像差WS(x,y)可以表示为

由（4）式可知，样品表面所在表面离焦所导致的波像差主要由离焦量S和球面波的NA决定，波面误差中包含着离焦项和球差项，用37 项Zernike条纹多项式对波面进行拟合可得

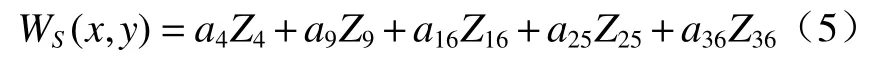
式中：Z4为离焦项；Z9、Z16、Z25和Z36分别为初级球差项、二阶球差项、三阶球差项和四阶球差项；a4、a9、a16、a25和a36分别为对应的泽尼克多项式系数。结合（4）式和（5）式，可以建立离焦项系数Z4与离焦量S以及NA之间的关系式为

1.2 检焦系统光路设计

本文设计的检焦系统光路如图2所示。He-Ne 激光器发出一束波长为632.8 nm 的线偏振光，经过扩束准直系统后，平行光出射至偏振分光棱镜，分成了两束振动方向相互正交的透射光P 光和反射光S 光。返回的两束光再次经过偏振分光棱镜、分光棱镜透射通过λ/4 波片，此时，参考光与测试光变成左旋与右旋圆偏振光，两束光经过共焦放置的2 片透镜，最后成像在微偏振片阵列相机靶面上，经过微偏振阵列后的两束光产生干涉，分别产生了恒定的0、π/2、π、3π/2 和的相位差，通过四步相移算法获得波像差。

图2 同步相移显微干涉检焦系统光路图Fig.2 Optical path diagram of synchronous phase-shifting microscopic interference focal detection system

2 实验与分析

2.1 参考臂与测试臂物镜差异标定

Linnik 型显微干涉系统的优点在于在参考臂中加入了与测试臂参数完全相同的显微物镜，减小了物镜误差给检焦带来的影响，但是2 个物镜在光学特性上依然会存在一定的差异，因此需要测量显微物镜之间的波像差，从而在实际检焦时对由于显微物镜差异带来的误差进行补偿。如图3所示，图3（a）为参考臂物镜波像差，其PV=0.422 λ，RMS=0.054 λ；图3（b）为测试臂物镜波像差，其PV=0.409 λ，RMS=0.048 λ；图3（c）为2 个物镜之间的旋转对称项成分的误差，其PV=0.014 9 λ，RMS=0.003 3 λ，该成分的误差将会在实际检焦时的干涉波像差中被消除。

图3 两个显微物镜波面对比Fig.3 Comparison of wave surfaces of two micro-objectives

2.2 基于波像差判据的检焦方法仿真分析

为了验证基于波像差判据的检焦方法的可行性与检测精度，采用NA为0.5 的显微物镜，波长为632.8 nm，在Zemax 光学设计软件中对其进行仿真。当离焦量S在显微物镜有效焦深范围内（-500 nm,500 nm）变化时，得到的离焦量值与实际离焦量的值之间误差曲线如图4所示。由图4 可知，当离焦量在有效焦深内变化时，误差在3 nm 以内变化，其误差主要来源于在处理仿真得到的波面数据时，为了与实验得到的波面分辨率保持一致，缩小了分辨率，导致了对波面进行拟合时产生了误差，据此可得基于波像差判据的检焦算法精度已经可以达到纳米级。

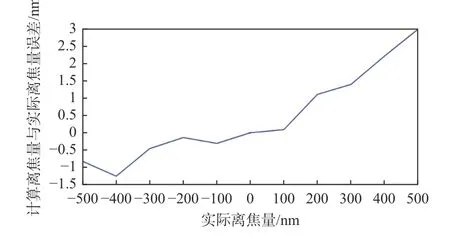
图4 离焦量的检测误差Fig.4 Detection error of defocusing amount

同时该检焦算法是根据波像差的变化来判断离焦量，因此对离焦量的探测灵敏度依赖于波像差的检测灵敏度，而对于干涉系统来说，通常其检测灵敏度为λ/1 000，根据（5）式离焦量与干涉波像差之间的关系，可得其在NA=0.5 时，离焦探测灵敏度为4 nm。为了验证该离焦探测灵敏度的正确性，设置离焦量为4 nm，得到其干涉波像差PV 值为0.002 λ，但是在实际测量时，受干涉仪波像差检测灵敏度影响，检焦灵敏度会略低于理论值4 nm。

2.3 实验结果与分析

根据上述计算方法，在离焦位置处采集同步相移干涉图，测得其干涉波像差并解耦出离焦量，再驱动高精度的压电陶瓷微位移器（PZT）根据离焦量的大小与方向调整至准焦面。

离焦检测结果，如图5所示，分别为待测面离焦时同步相移干涉图5（a）；解包相位得到的包含离焦量信息的波面图5（b）；37 项Zernike 条纹多项式拟合重构的完整波面图5（c）；离焦项与球差项重构的波面图5（d）。其中z轴为波面相位，此时，离焦项与球差项拟合波面PV 值为0.05 λ，RMS=0.013 λ。

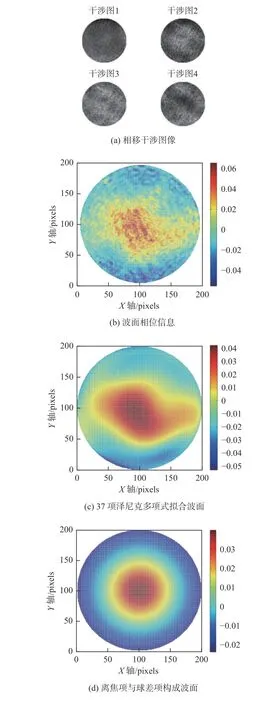
图5 离焦检测结果图Fig.5 Diagram of defocusing detection results

将此时对干涉波像差拟合出的离焦系数-0.042 1 以及NA=0.5 代入（6）式计算得到离焦量为204.45 nm，此时由于离焦项系数为负，为焦内离焦204.45 nm，因此调节PZT 向焦面方向即平面所在平台向下移动204.45 nm，此时得到的实验结果如图6所示，其中图6（a）为由离焦及球差项表征的波面分布，PV=0.017 3 λ，RMS=0.005 4 λ；图6（b）为离焦情况下与准焦时离焦项与球差项Zernike项系数的变化，离焦项系数已由-0.042 1 变化为0.000 2，接近于零，代入（6）式可得离焦量为焦内离焦1.19 nm，离焦基本已经消除。

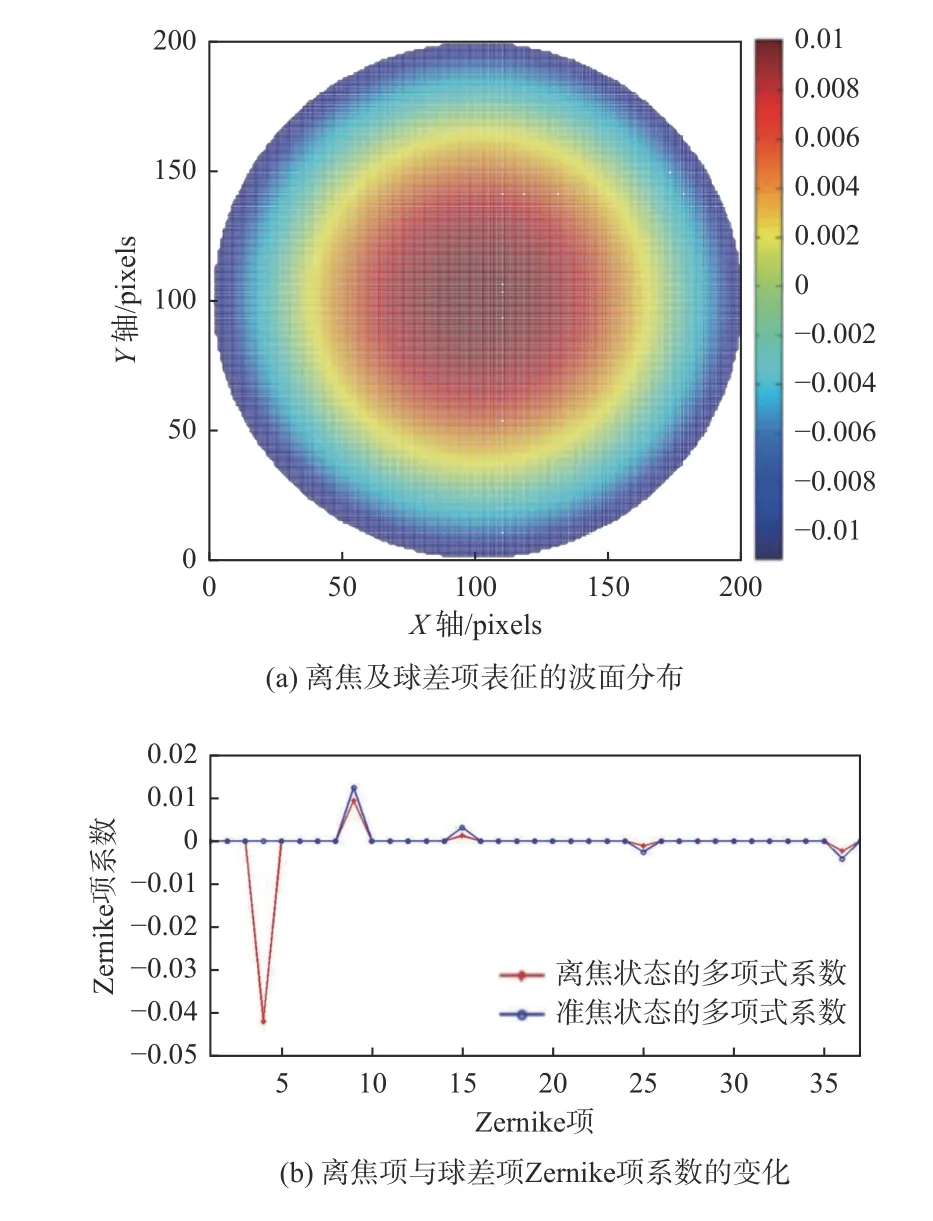
图6 准焦时检测结果图Fig.6 Diagram of in-focus detection results

为了进一步验证该检焦系统的正确性，以上述实验得到的准焦位置为参考位置，分别向焦内方向和焦外方向移动PZT，设置步长为100 nm，移动范围为（-500 nm，500 nm），对比计算出的离焦量S1与实际离焦量S2即PZT 位移量，其最大误差小于9 nm，误差平均值为4.55 nm，误差均方根为2.68 nm，因此该系统的检焦精度达到10 nm，如图7所示。

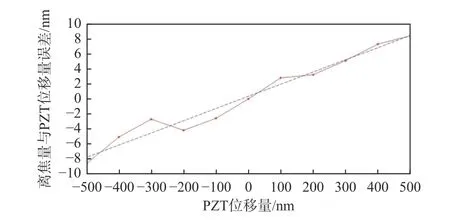
图7 离焦量实验检测误差Fig.7 Experimental detection error of defocusing amount

在大数值孔径NA波像差的离焦解耦时，来源于光学元件的误差会对光路产生球差影响；对干涉光路参考臂与测试臂的误差作了详细的测量和标定，但是由于测量标定不能够严格地确认两臂之间的残余像差，存在一定误差残留。除此以外，对焦范围内检焦精度的误差主要来源于PZT 调焦时的振动影响。另外由于本系统是基于显微干涉测量波像差，因此还会存在干涉光路较长，空气扰动带来的一定误差。

3 结论

本文提出了一种基于波像差判据的同步相移显微干涉检焦方法，相比于已有的检焦方法，提高了检焦系统的准确度与稳定性。本文建立了离焦量与波像差之间的关系模型，提出了大数值孔径NA的显微物镜波像差中离焦量计算方法，搭建了检焦实验装置，仿真验证了该方法的正确性，离焦探测灵敏度可达4 nm；实验验证了该方法可以准确地得到准焦面的位置，检焦精度最优可以达到10 nm，表明了基于波像差判据的同步相移显微干涉系统的可行性。