连续排水边界下考虑起始坡降的软黏土固结解
2021-09-23李传勋
陈 余,李传勋
(江苏大学土木工程与力学学院,江苏,镇江 212013)
经典太沙基固结计算时,常将排水边界看作理想化的完全透水边界,事实上,当砂垫层透水性不良时,土层的边界条件大多数介于透水与不透水之间。同时,太沙基一维固结理论中也存在初始条件与边界条件相矛盾的逻辑问题,太沙基固结理论中的排水边界在初始的瞬间超静孔压有突变,忽略了固结过程本身是一个连续的过程。基于此,梅国雄等[1]提出了介于透水和不透水之间的连续排水边界条件,对太沙基一维固结理论进行了有益的补充。
与完全透水边界、完全不透水边界及第三类排水边界相比较,连续排水边界具有适定性,适用于大多数软黏土地基的边界排水情况,能严格满足固结模型的初始条件,且其在一定条件下能够退化为完全透水边界,因此进行基于连续排水边界下土体固结理论的研究具有一定的理论意义和实际意义。张国英等[2]建立了连续排水边界下一维均质地基固结模型,采用有限傅里叶变换方法求得超静孔压解答,分析了不同排水边界界面参数下固结性状的异同。蔡烽等[3]基于ABAQUS有限元软件开发了连续排水边界条件下固结计算的子程序,并将计算结果与连续排水边界下固结解析解对比验证子程序的可靠性,从而在技术上提供了连续排水边界应用于实际有限元计算的途径。在此基础上,冯健雪等[4]给出了单级加载下考虑连续排水边界的土层一维固结解析解,其在求解过程中连续排水边界是基于瞬时加载建立的。Feng等[5]建立了同时考虑自重与外荷载引起的初始孔压非均布和连续排水边界的地基一维固结模型,并给出了该模型的解析解。需要指出的是,以上基于连续排水边界的固结理论均没有考虑土体的非线性固结特性。
事实上土体的非线性压缩和渗透特性对土体固结性状的影响不可忽视。基于此宗梦繁等[6]在初始有效应力和固结系数保持不变的基本假定下,得到了连续排水边界下土体一维非线性固结模型解析解。宗梦繁等[7]进一步考虑土体的流变固结特性,得到瞬时和单级加载下考虑连续排水边界的土体一维流变固结解析解。田乙等[8]在连续排水边界下采用分数阶Kelvin模型来描述饱和土体的流变特性,得到了分数阶导数黏弹性饱和土体一维固结半解析解。李称等[9]在已有的简化降解固结模型基础上引入连续排水边界条件,建立了不同排水边界下饱和城市固废一维降解固结模型及其解析解。江文豪等[10]采用大应变几何假定,研究了考虑连续排水边界下饱和软土的一维大变形固结问题。Zhang等[11]分析了连续排水边界条件下竖井地基的超孔隙水压力和平均固结度,探讨了顶面排水能力、涂抹和井阻效应对固结性状的影响。Tian等[12]在多级荷载和连续排水边界条件下,利用超孔隙水压力叠加公式,得到了超孔隙水压力和固结度的解析解,得到了任意时变荷载作用下更一般的连续排水边界。由此可见,尽管目前对连续排水边界下土体的线性和非线性固结问题均有一定研究,但前述的对连续排水边界下固结理论的研究均假定土中渗流遵从达西定律,而实际工程中软黏土中的渗流在低水力坡降下常常会出现偏离达西定律的现象。试验和实测均表明软黏土中渗流在低水力坡降下可能会出现偏离达西定律的现象[13 − 17]。其中Mitchell和Younger[14]的实验数据显示,在低水力坡降下的饱和黏土中渗流的实测流速很小甚至没有渗流发生,这是在水力坡降较小的情况下,由于低渗透性黏性土中有粘滞阻力的存在所导致的。为进一步简化饱和软黏土中水的这一渗流现象,Miller和Low[18]提出了考虑初始水力坡降的渗流模型,即当水力坡降i小于起始水力坡降i0时,土中无渗流发生;只有当水力坡降i大于i0时,土中才会发生渗流。需说明的是,即使土中渗流在低水力坡降下没有完全停止,但考虑起始水力坡降的渗流模型可看作是低水力坡降下流速极其微小的一种简化模型,故有必要对考虑起始水力坡降的固结理论开展研究[19 − 27]。目前考虑起始水力坡降的固结理论均认为土层的排水边界为完全透水或完全不透水,但实际中土层边界的透水性并不是完全理想化的,其排水边界孔压随时间指数衰减的连续排水边界更符合实际工况,尤其对存在起始水力坡降的黏性土的排水边界更适用。
本文同时考虑软黏土中渗流存在起始水力坡降以及土层表面的连续排水边界特性,对软黏土地基一维固结理论展开研究,并着重分析边界系数b和起始水力坡降i0对固结性状的影响。本文提供的固结理论模型适用于大多数软黏土地基的排水固结计算,尤其是黏粒含量较多导致的土中渗流在低水力坡降下存在起始值的工况,进而为该类工程地基的固结变形计算提供重要的理论支持。
1 边界条件的分析及固结模型的建立
如图1所示,无限均布荷载q0施加于均质黏土层,黏土层厚度为H,土层顶面是连续排水边界,其界面排水系数为b,土层底面为完全不透水边界,土体压缩模量为Es。

图1 软土地基一维固结模型Fig.1 One-dimensional consolidation model of soft ground
本文在建立固结模型时采用了Terzaghi固结理论中除软黏土中水渗流服从达西定律以外的其他基本假定。
土中渗流考虑存在的起始水力坡降,其值为i0,以重力方向向下为正,则土中渗流规律[18]可以表示为:
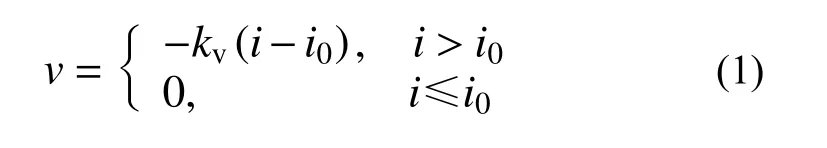
式中:i为水力坡降;kv为黏土层的渗透系数;v为黏土层中水的流速;i0为起始水力坡降,其值可以由黏性土的渗透试验来确定。渗透系数的室内测定可采用常水头法获得,通过测试不同水头下的渗透系数,绘制出渗流速度和水力坡降的关系曲线,曲线与水力梯度坐标轴的交点可确定起始水力坡降。土层顶面连续排水边界处的孔压应满足[1]:
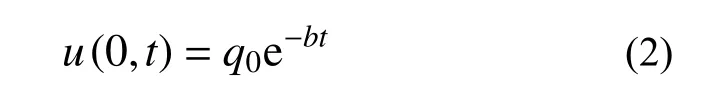
式中:u为超静孔隙水压力;t为时间;b为连续排水边界界面系数,反映土体排水能力,界面参数是通过孔隙水压力传感器测量出的土体不同位置和时间的超静孔隙水压力再反演获得[28]。b值越大边界排水性越好,当b→∞,连续排水边界退化为完全透水边界。土中渗流存在的起始坡降必然引起固结过程中的边界移动,记t时刻移动边界距离透水面的距离为h(t),此时渗流锋面z=h(t)处超静孔隙水压力u及水力坡降i应该满足的边界条件为[19]:
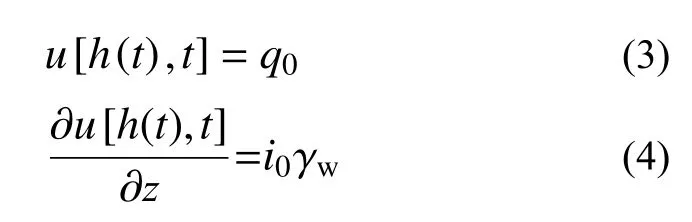
式中:z为深度; γw为水的重度。
根据侧限条件下孔隙比变化与竖向有效应力变化间的关系,可建立渗流前锋以上土体的一维固结控制方程:

式中,cv为固结系数,cv=kvEs/γw。控制方程对应的连续排水边界为式(2),起始水力坡降引起的移动边界表达式为式(3)和式(4)。模型的初始条件为:

2 固结模型的解析解答
2.1 渗流移动边界未到土层底面的解析解
至此,该问题对应的固结模型已建立完备。
为方便求解做如下变量代换,令:
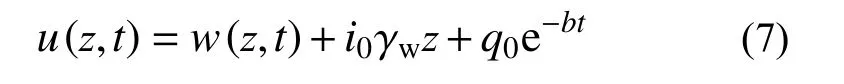
将式(7)代入式(3)~式(6)中,则固结控制微分方程、边界条件及初始条件转化为:

将w(z,t) 和q0e−bt按关于z的固有函数进行傅里叶正弦级数展开,即:




进而t时刻z≤h(t)的超静孔压表达式为:

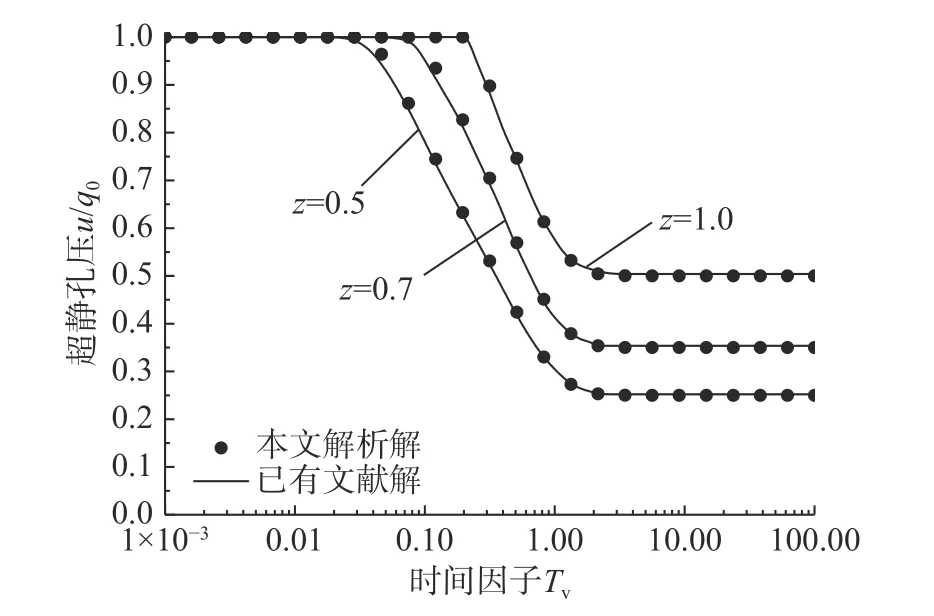
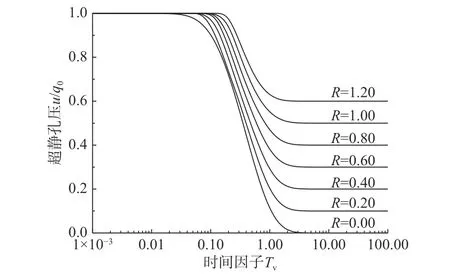
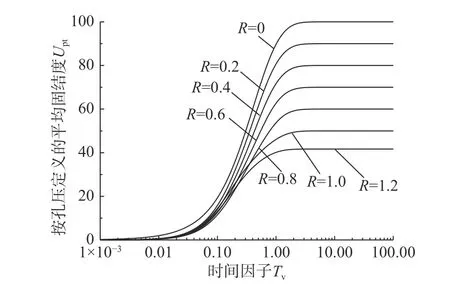
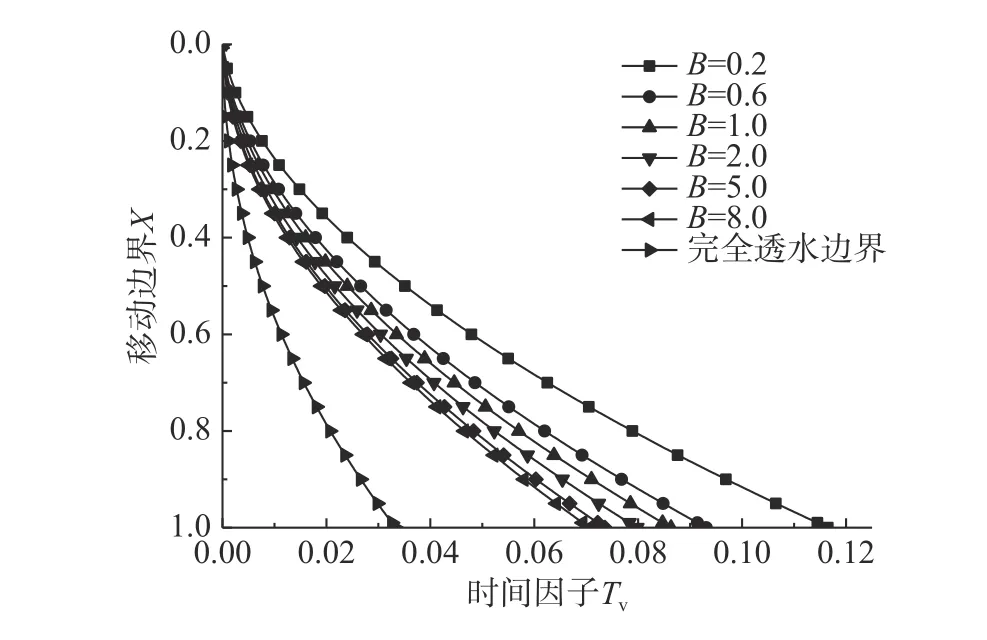
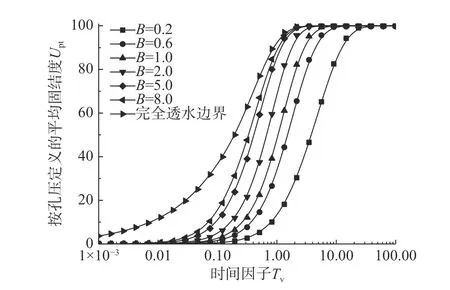
当h(t) 当t趋近于无穷(固结已完成)时,如果渗流锋面仍不能至土层底面,此时土中残留孔压沿深度分布为: 根据式(3)表达的移动边界处超静孔压需满足的条件,结合式(14)超静孔压在z=h(t)处的表达式,可得到渗流移动边界随时间变化规律为: 应用无量纲变量,式(15)对应的无量纲表达式为: 本研究初步提示,早期足量肝素用于STEMI患者,有助于改善冠脉血流、改善心功能,且并不增加出血事件。但,本研究为单中心研究,样本数量有限,还需要以后更大样本量的研究。 按t时刻孔压定义的平均固结度Upt为: 将超静孔压表达式代入,平均固结度可进一步表达为: 根据有效应力原理,可将有效应力表达为: 进而可得到t时刻土体沉降量St为: 式中: σ′为有效应力;Es为土体压缩模量,在无侧向变形条件下,竖向应力和应变的比值,反映土体对竖向压缩变形的抵抗能力。令固结时间向无穷远处发展,根据残留孔压分布可得到移动边界能到达土层底面与移动边界始终不能到达土层底面的最终沉降量,其表达式为: 根据按变形定义的计算公式Ust=St/St→∞,最终得到按变形定义的平均固结度Ust。 当渗流移动边界到达土层底面时,可在式(14)中令h(t)=H获得t时刻超静孔压表达式为: 在渗流锋面能发展至底面的条件下,当t趋近于无穷(固结完成)时,此时残留孔压沿深度分布为: 根据平均固结度的定义: 得渗流移动边界已到达土层底部的平均固结度Upt: 根据不考虑侧向变形条件下的压缩量计算公式算得土层沉降量St为: 进而得到按变形定义的平均固结度Ust为: 前文提到b是排水边界的界面系数,其反映地基土体边界的排水性能,其值越大,边界的透水性越好;相反,其值越小,边界的透水性越差。如果令b趋近于无穷大,那么连续排水边界条件下的固结模型就退化为完全透水边界下考虑起始比降的一维固结模型。渗流移动边界未到达土层底面的超静孔压计算式退化为: 当0 当h(t) 式(29)和式(30)正是王坤等[21]初始孔压均布条件下考虑起始比降的一维固结解解析解。渗流移动边界X与时间因子Tv的关系式退化为: 渗流移动边界未到达土层底面时按孔压定义的平均固结度和沉降量的计算式退化为: 渗流移动边界到达土层底面时按孔压定义平均固结度和沉降量的计算式分别退化为: 如果忽略考虑起始水力坡降的存在,考虑起始水力坡降的渗流定律就退化为达西定律,此时如果令i0=0(R=0),超静孔压的解析表达式退化为: 式(36)恰好是张国英等[2]连续排水边界条件下均质地基单面排水一维固结解析解。按孔压定义的平均固结度和沉降量的计算式分别退化为: 以上退化说明,现有的仅考虑起始水力坡降而忽略复杂排水边界的固结解析解及达西定律下考虑连续排水边界的固结解析解均是本文解析解的特例。 由3.1小节知,当B取值足够大可近似看作完全透水边界,再根据文献[27],将完全透水边界下的超静孔压随时间变化的关系曲线与B=100 000时本文模型的超静孔压与时间的关系曲线进行对比,发现两者曲线几乎重合,如图2所示,再次验证了本文固结解析解的正确性与可靠性。 图2 已有文献解与本文解析解的对比(B=100 000)Fig.2 Comparison between existing solution in literature and analytical solution (B=100 000) 影响本文固结模型性状的主要因素是土中渗流存在的起始水力坡降和边界透水性能两方面。因此,本文将重点分析无量纲变量R及反映界面参数b的无量纲变量B对固结性状的影响。 如图3所示,某工程地基土体为均质饱和软土,其上堆载了5 m高的路基填土,路基填土对地基土层顶面瞬时施加了100 kPa的恒荷载,整个地基土层处于正常固结状态(土层自重作用下的固结变形已完成),地基土层底部为完全不透水层。土层固结计算的相关参数见表1。 图3 黏性土层的边界条件Fig.3 Boundary conditions of cohesive soil 表1 计算分析所用参数Table 1 Parameters adopted in the following analysis 对同一地基土层而言,R值反映了外荷载和起始水力坡降的影响。故研究不同R值下地基土体的固结性状也就反映了荷载和起始水力坡降对固结性状的影响。 起始水力坡降i0的存在致使土中超静孔压不能完全消散,且当i0取值大于q0/(γwH)(R>1)时,移动边界始终不能达到土层底面,在施加荷载后瞬间从排水面至渗流移动边界处的土层发生渗流。当i0取值小于q0/(γwH) (R<1)时,移动边界以下至不排水面的土层不发生渗流,但随固结时间的推移,渗流移动边界将最终发展至土层底面,整个土层均会发生渗流,即渗流锋面最终能发展至土层底面。图4分别给出当R>1和R<1情况下的移动边界随时间的发展过程。从图中可发现,渗流移动边界向土层底部发展的快慢与R值的大小密切相关,R值越大,移动边界下移速度越慢,R值越小,渗流移动边界下移速度则越快。当R值大于1时,渗流前锋则不能到达土层底面,其最终停留位置为1/R。在连续排水边界下,R值对固结性状的影响与完全透水边界下相比并未发生明显改变,其固结性状与文献[24]描述的固结性状基本一致。 图4 R对移动边界的影响Fig.4 Influence of R on moving boundary 图5为Tv=0.3时超静孔隙水压力随深度变化曲线。可发现同一深度处达西定律下(R=0)土中超静孔压残留值最小,超静孔压残留值会随R值增大而增大。这说明R值影响超静孔压的消散速率,其消散速率随R值增大而逐渐减慢。同时,达西定律(R=0)下随着固结时间的推移,超静孔压能够在固结完成时消散完成,即超静孔压的最终残留值为0。图6为不同R值下z/H=0.5处超静孔压随时间消散过程,可发现达西定律下超静孔压消散最快,且其能够最终消散至0。R值一旦大于0,则超静孔压就不能最终消散至0。且R值越大,超静孔压消散速率越慢,同时刻下超静孔压残留值越大。 图5 R对z/H -u/q0曲线的影响(Tv=0.3)Fig.5 Influence of R on z/H -u/q0(Tv=0.3) 图6 R对u/q0-Tv曲线的影响(z/H=0.5)Fig.6 Influence of R on u/q0-Tv(z/H=0.5) 以上超静孔压消散规律直接反应至土层固结度表现为,当R=0(达西定律)时,由于最终超静孔压能够完全消散,此时平均固结度能到达100%。一旦R值不等于0,鉴于超静孔压最终不能完全消散,则土层平均固结度最终值就不能到达100%。同一时刻下平均固结度随着R值的增大而减小。且R值越大,孔压消散完成的时间会越短,因此固结度达到稳定值的时间也越短,如图7所示。 图7 R对固结度Up的影响Fig.7 Influence of R on average consolidation degree Up 界面系数b的大小反映了排水面边界的透水性情况,通过对b值大小的控制,可以得到不同透水性边界条件的固结模型。事实证明,排水边界透水性的强弱对固结性状有着显著影响。 随着界面排水能力的降低(B值变小),土中超静孔隙水压力消散减慢,渗流移动边界下移速率亦会减慢,如图8所示。B值越小,移动边界到达底部的时间越长;B值越大,移动边界到达土层底部的时间越少,当B=100 000时,连续排水边界可以近似看作完全透水边界,此时移动边界随时间的下移速度最快。 图8 B对渗流移动边界的影响Fig.8 Influence of B on moving boundary 图9为不同界面参数下Tv=0.8时超静孔压随深度分布曲线图。通过计算发现渗流移动边界在Tv=0.8时已移动至土层底面。从分布曲线中可发现,同一深度处超静孔压值随B值的减小而逐渐增大。说明该时刻土中超静孔压在完全透水边界下消散最快,残留的超静孔压值最小。随着B值的减小,超静孔压消散速率逐渐减慢,土中残留的超静孔压逐渐增大。 图9 B对z/H-u/q0曲线的影响(Tv=0.8)Fig.9 Influence of B on z/H-u/q0(Tv=0.8) 同样的,固结性状在某深度处超静孔压随时间消散曲线中也有所展现。图10为在z/H=0.1处的超静孔压随时间变化的曲线,该组曲线进一步描述了无量纲变量B对超静孔压消散的影响。B值越大,某深度处的超静孔压消散速率越快,同时也越接近于完全透水边界下的u/q0-Tv曲线。这样的固结性状在固结度随时间发展曲线中进一步展现,如图11所示,B值越大,相同时间下地基固结度越高,且完全透水边界下土层的平均固结度最大。 图10 B对u/q0-Tv曲线的影响(z/H=0.1)Fig.10 Influence of B on u/q0(z/H=0.1) 图11 B对固结度Up的影响Fig.11 Influence of B on average consolidation degree Up 考虑软黏土地基中存在的不同透水性边界及土中渗流存在的起始水力坡降,在太沙基一维固结理论的基础上重新建立并推导了一维固结控制方程,得到其解析解,结论如下: (1)给出了基于连续排水边界和起始水力坡降的软土一维固结解析解。该解答为同时考虑起始水力坡降和不同透水性边界的实际软土固结计算提供了可供参考的计算方法。 (2)本文解可退化为考虑起始水力坡降的一维线性固结解析解,也可退化为达西定律下考虑连续排水边界的软土一维固结解析解。这两种情况下的解析解均是本文解析解的特例。 (3)连续排水边界下起始水力坡降对软黏土固结性状影响与完全透水边界下相比,并未发生明显改变。 (4)连续排水边界对起始水力坡降所引起的移动边界下移速度影响较大,透水性越差,移动边界下移速度越慢。但总体而言,考虑起始水力坡降后连续排水边界排水能力对超静孔压消散的影响与达西定律下相比没有发生明显改变。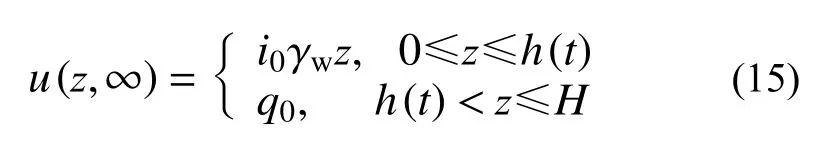
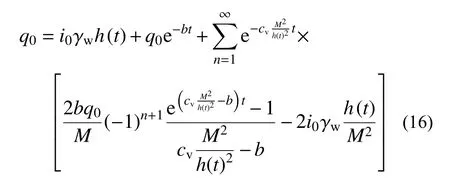
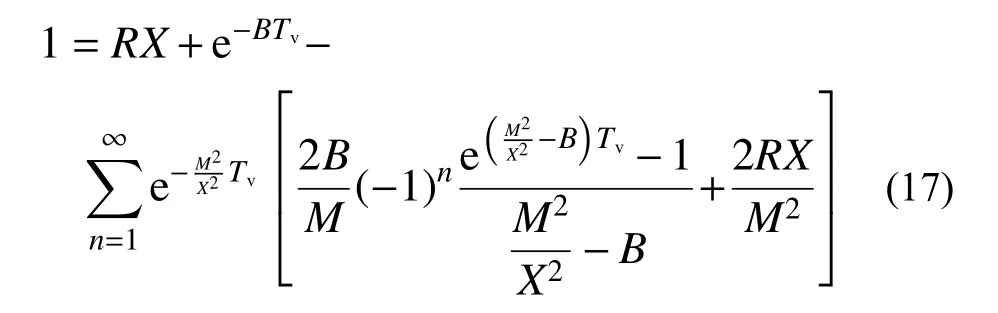
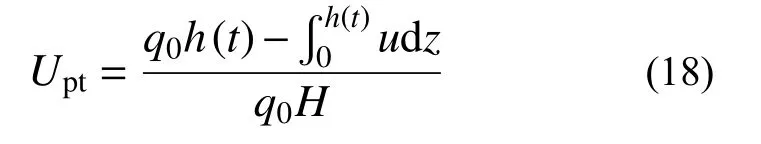
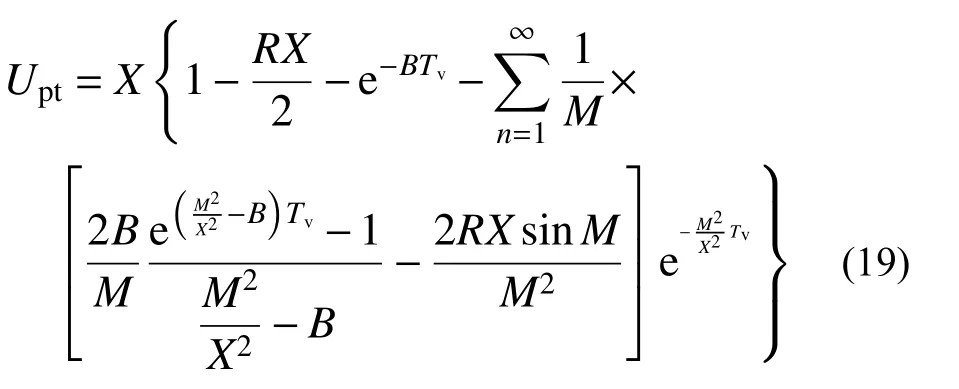

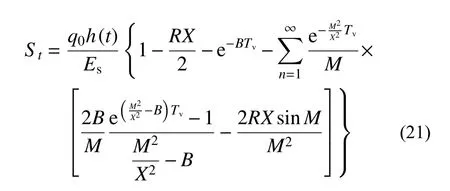

2.2 渗流移动边界到达土层底面的解析解


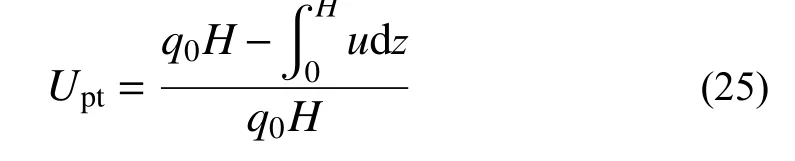



3 解析解的退化验证
3.1 基于连续边界条件的固结模型解析解的退化

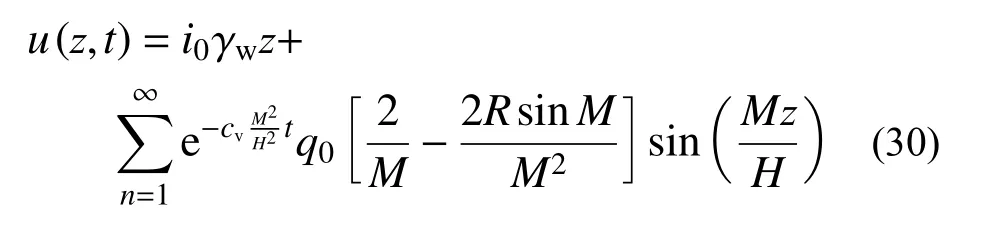
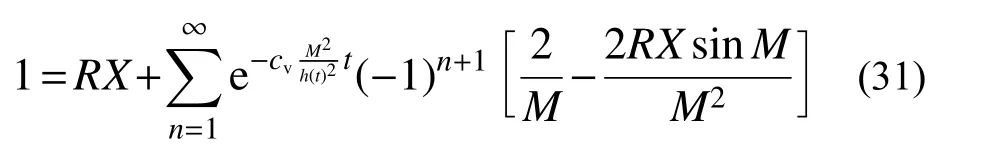

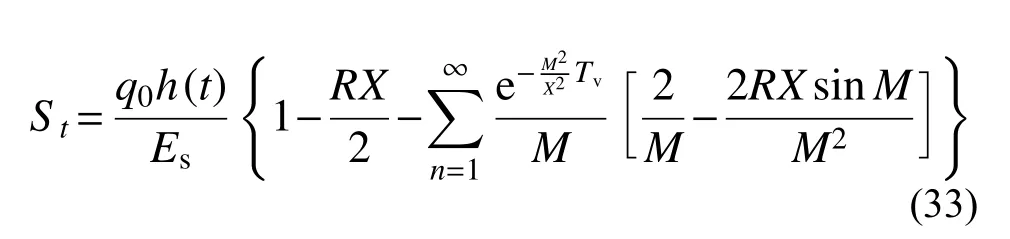
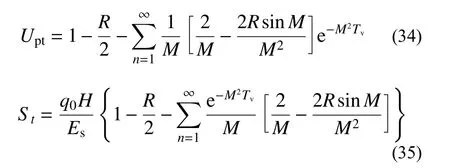
3.2 不考虑起始水力坡降时解析解的退化

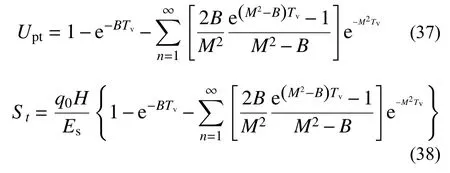
3.3 本文解析解与已有文献的对比
4 固结性状分析


4.1 基于R对固结性状的影响


4.2 基于B对固结性状的影响


5 结论
