非线性结构地震响应的神经网络算法

2021-09-23许泽坤

工程力学 2021年9期

许泽坤，陈隽

(同济大学土木工程学院，上海 200092)

一方面，过去几十年内发生的一系列地震灾害表明，有必要对建筑进行基于性能的抗震设计，以更好地满足不同的抗震需求[1]。为此，需要进行不同等级的建筑物弹塑性地震响应时程分析[2]。然而，由于其高昂的计算成本，很难快速完成大量不同地震动作用下单体建筑的非线性地震响应分析。在基于蒙特卡洛模拟[3]或增量动力分析[4]的结构性能评估中，这一矛盾尤其突出。

另一方面，随着城市系统安全概念的普及，防灾减灾研究正由建筑单体扩展至城市建筑群，城市区域抗震分析越来越受到关注。如何快速预测城市建筑群的地震响应成为首要技术难题[5 − 6]，当前的城市震灾模拟依然以简化模型与静力分析为主[7]，尚难实现可比拟单体结构的高精度实时计算。采用超级计算机是一种可能的解决方案[8 − 10]，但其普及性现阶段仍受限于计算资源的开放程度。因此，发展适用于边缘计算场景的结构非线性地震响应新型计算方法是值得深入研究的问题。

随着硬件性能的快速提升与深度学习技术的普及，人工神经网络(artificial neural network, ANN)为结构非线性地震响应计算问题带来了全新的可能。例如，ANN作为方程的隐式表达，通过发展通用的函数逼近方法，可实现不同非线性微分方程的求解[11 − 12]。目前，通常采用具有少量隐层的多层感知器(multilayer perceptron, MLP)，比较适用于具有简单约束的低维非线性求解[13]。对于具有物理背景、工程约束的求解问题，已有研究使用长短期记忆(long short-term memory, LSTM)神经网络与卷积神经网络(convolutional neural networks,CNN)来解决Navier–Stokes方程以及高维数据中的流体模拟[14 − 16]。其他相关工作包括通过强化学习降低量子多体问题的复杂性[17]；构造特定损失函数的全连接神经网络也被用于求解波动方程问题[18]等。

以上工作表明了ANN求解微分方程的可行性，但用于地震作用下的结构动力方程求解依然存在相当的挑战。一方面，结构的恢复力特性使其在往复荷载下表现出复杂的非线性行为，简单架构的MLP难以捕捉到准确的滞回特征。另一方面，建筑结构作为复杂多自由度系统具有大量物理参数，很难建立完整的神经网络映射模型以逼近其精确解。因此，结合分析目标先固定部分物理参数(如层数、层高、恢复力特性等)，转而寻求结构响应的ANN近似解是一种更加经济的做法。沿着这一思路，Lagaros等[19]设计了传统非线性分析与MLP相结合的时程预测方案，由于使用人工地震波进行训练，最终的预测效果不甚理想。Kim等[20]借助CNN提取滞回特征，建立了从激励与滞回曲线到结构峰值响应预测的复合神经网络模型，模型基于单自由度体系建立，需要大量数值计算结果作为训练集，目前尚未应用于复杂结构。Zhang等[21 − 22]先后使用LSTM网络与CNN建立了结构地震响应时程的预测模型，在给定数据上进行，取得了良好的响应预测效果。该模型对地震动数据集进行了下采样和低通滤波的预处理，影响了对响应时程高频成分的预测。此外，上述模型采用固定的超参数与输入序列长度，没有给出不同工况下的参数选取原则，给未知地震动下的应用带来了困难。

显然，有必要提出一种新的神经网络模型，实现对任意长度结构响应时程的计算，并尽可能放松对训练数据集的预处理要求。同时，新模型应该对不同地震动和结构具有良好的泛化能力，并具有相对较少的调试参数以方便应用。基于上述认识并受前述学者工作的启发，本文基于LSTM网络提出了一种数据驱动的结构非线性地震响应预测方法，替代传统数值积分求解方法以满足不同计算场景需求。模型采用了新的滑动时间窗思路进行递推预测，以模拟结构动力方程的积分求解过程。利用模型对两个框架结构的地震响应预测结果，分别从地震动频谱、地震动幅值、结构模型等方面进行了泛化能力分析，验证了模型的适用性与准确性。

1 LSTM模型

LSTM神经网络是循环神经网络(recurrent neural network, RNN)的一种变体，由Hochreiter等[23]在1997年首次提出，最初用于处理RNN训练中的梯度消失以及数据的长期依赖问题[24]。相比基本的RNN，LSTM单元包含了3个门(gate)结构：输入门、输出门和遗忘门，用以调节单元内部的信息流。LSTM被广泛用于语音识别[25]、手写识别[26]等方面，成为最成功的神经网络结构之一。

1.1 网络结构与参数

针对本研究目的，LSTM网络采用了堆叠式结构：顺序连接3个单向LSTM层和1个全连接层(记为FC层)，如表1所示。每个LSTM层均包含200个神经元且使用双曲正切激活函数。

表1 LSTM网络结构Table 1 LSTM network structure

模型的输入数据包括时间窗口内的地震动时程和结构响应时程。本文将输入地震动时程记为A=[a1,a2,a3,···,an]T∈Rn，其中，n表示输入时间序列的长度，即滑动窗口大小。将输入的结构响应时程记为D=[d1,d2,d3,···,dn]T∈Rn×f，其中，f为结构响应的预测点数量(例如结构层数)。由此，输入数据可以表示为一个n×(f+1)维数组，记为X=[A,D]∈Rn×(f+1)。

输出数据为结构在当前递推步的响应，与输入相似，可表示为一个多维数组D∈Rm×f，其中，m表示输出时间序列的长度。本文中为了保证预测精度，每次仅预测单位时间的结构响应，即m=1。然而当，任务较为简单(如线性响应预测)时，可以令m>1以提高执行效率。

训练中，对kernel权重执行Xavier均匀分布初始化，对门权重执行正交初始化。使用了Adam优化器与均方误差损失函数。为了防止出现过拟合，加入了L2 正则化，参数λ=0.01。在学习率的选择上，虽然Adam优化器被认为具有自适应梯度特性，但在实际使用中发现使用衰减的学习率可获得更好的效果[27]。本文对学习率执行按倒数衰减，以保证训练过程在后期趋于稳定，学习率衰减曲线如图1所示。本文模型的训练基于Tensorflow机器学习平台，并在搭载有Intel(R)Core(TM) i5-8600 CPU @ 3.10 GHz和NVIDIA GeForce GTX 1070Ti GPU的个人计算机上完成。

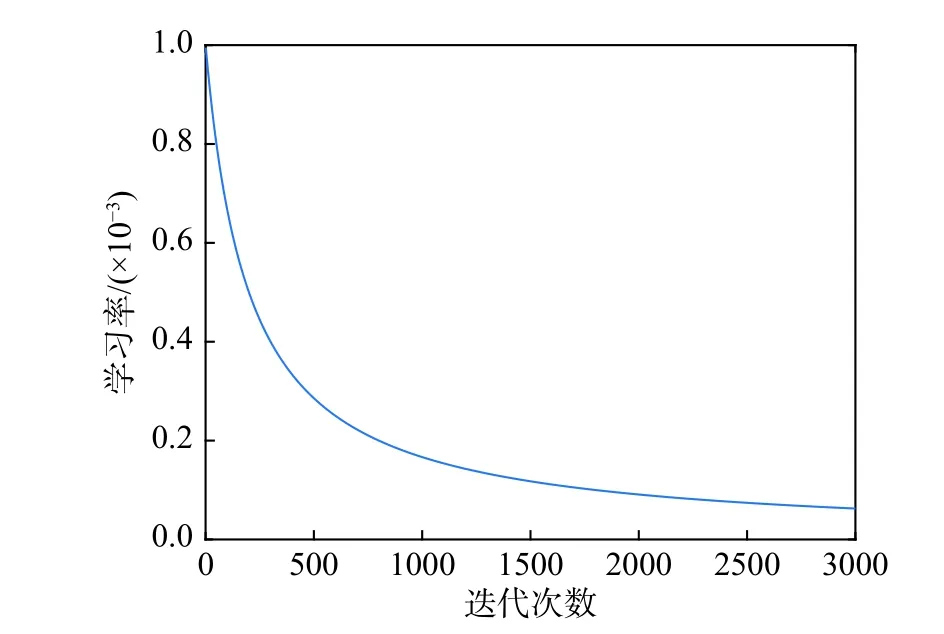
图1 学习率衰减曲线Fig.1 Learning rate decay curve

1.2 滑动时间窗

现有结构地震响应预测的研究思路多为建立完整地震动输入到响应时程的映射模型。此方式需要固定输入、输出的时间序列长度，且可能导致数据量与模型的矛盾：为了提高模型对不同地震动的泛化能力和预测精度，需要增加神经元数量和输入序列长度，但有限的训练数据可导致复杂网络难以训练或出现严重的过拟合问题。受到传统数值积分求解方法与其他领域工作[28 − 29]的启发，本文使用滑动时间窗的预测方式实现如下目的：

1) 对于整条时程，添加时间窗的LSTM神经网络关注时程的局部特征，适合非线性响应预测的需求，并且与传统方法类似的递推形式有助于形成具有更强精确性与可解释性的神经网络。

2) 对于单步运算，LSTM网络考虑了序列中不同输入间的关联性，可以仅通过有限的响应时程学习到物理现象在高维空间内的隐含特征表达。

如果将LSTM网络的映射关系记为函数ft，并将从第i个采样点开始的序列长度为n的输入数据记为Xi=[xi,xi+1,xi+2,···,xi+n−1]T，那么存在关系：

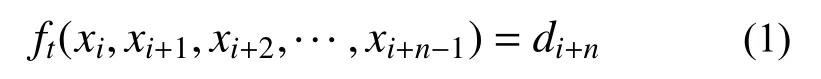
或

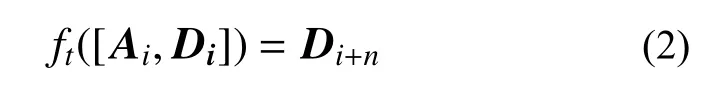
假设n=3，图2展示了滑动时间窗的预测流程。在完成当前时间窗 [i,i+n−1]内的数据预测后，将第i+n个采样点的输出响应作为已知，继续完成时间窗 [i+1,i+n] 内的数据预测。注意到i=1时，可以通过预测得到的最早的响应为Dn+1，即前n位响应数据需要作为已知条件提供。因此在时程信号前进行窗口长度的零填充操作，以实现完整的时程预测，这一点类似于数值积分方法的递推起步问题。

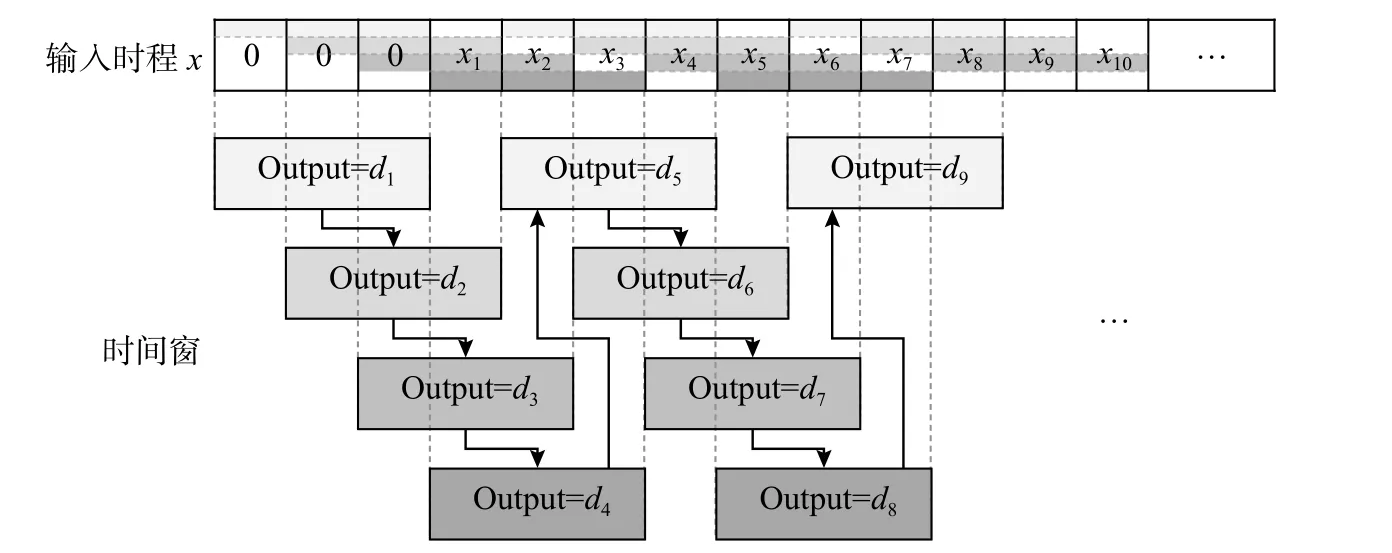
图2 滑动时间窗的预测流程Fig.2 Forecasting process with sliding time window

与传统方法相比，LSTM一方面仅对少量目标节点的响应参数进行更新计算，省略了多自由度系统中大量无用参数的求解过程，以换取更低的计算量和计算时间，同时神经网络天然的并行性使大批量地震动响应的同步预测成为可能。另一方面，输入中扩展的时间序列可以被视为潜在物理信息(速度、滞回状态等)的容器，LSTM通过学习到的权重参数对其进行高维空间中的提取，因此LSTM是对积分过程的鲁棒性隐式建模。但也因为这一性质，经过训练的LSTM模型只能描述单一结构的物理特性，无法应用在其他结构上。

综上，LSTM神经网络模型预测的运行流程如图3所示。左侧区域表示了神经网络的训练过程，右侧区域表示了基于滑动时间窗的递推预测过程。

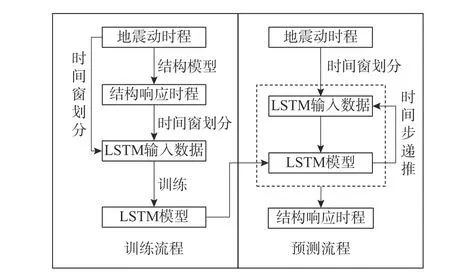
图3 LSTM模型的响应预测流程图Fig.3 Flowchart of response prediction of LSTM model

2 评价指标

对前述模型预测效果的评价，不同文献采用了不同的指标，包括MAE、MSE、Pearson相关系数、决定系数等有量纲指标和无量纲指标两类。本节分析上述指标用于结构响应拟合效果评价时的不足，进而提出针对性的改进指标。

2.1 有量纲指标

有量纲指标通常包括MAE、MSE、RMSE等。平均绝对误差MAE (mean absolute error)定义见下式：

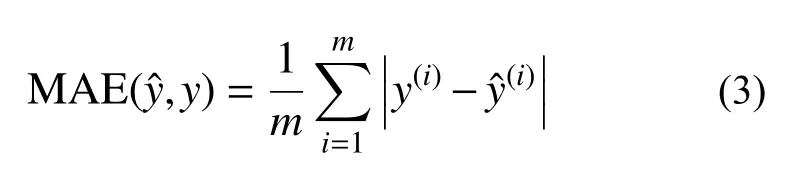
均方误差MSE (mean squared error)及均方根误差RMSE (root mean square error)的定义分别如下：

显然，有量纲指标的数值大小及其含义与目标变量的物理单位有关。当指标与目标变量的单位一致时，可以直观地反映误差的大小，但对于不同的地震数据集或响应预测值，有量纲指标难以进行横向比较。

2.2 无量纲指标

无量纲指标通常包括Pearson相关系数和决定系数。Pearson相关系数是用于衡量变量间线性相关程度的指标，取值范围[−1, 1]。

决定系数(coefficient of determination)通常记为R2，取值范围[0, 1]。决定系数可用于非线性拟合，它衡量了因变量受自变量的解释程度。R2值越接近1，拟合回归效果越好。

由于其归一化特点，无量纲指标更适合用于比较模型在不同数据集或问题上的优劣。

2.3 改进指标

将上述指标用于结构响应预测效果评估时，每个时程点的预测误差具有相等的累加权重，而实际上峰值响应的预测精度更具价值[30]。在现有的规范方法中，也常常把最大层间位移角等作为主要的控制指标。此外，无量纲指标Pearson相关系数与R2对相位过于敏感，数个采样点的相位差就可能造成数值的大幅变化。

针对上述问题，对常用的指标进行了改进以适用于响应预测效果的评价。以MSE为例，将调整后的指标记为加权均方误差WMSE (weighted mean squared error)，其算数平方根记为加权均方根误差WRMSE (weighted root mean square error)，即：

式中：w(i)为第i个采样点处的权重； |y|max为|y(i)|在整条时程上的最大值。

此外，使用峰值百分误差以评价预测模型在峰值点处的误差水平，计算方式如下：

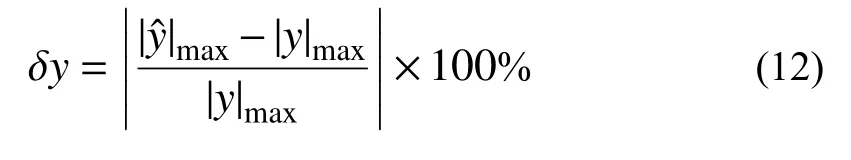
3 模型使用的案例分析

3.1 例1. 10层框架结构

某10层办公楼采用钢筋混凝土剪切型框架结构，依据现行国家规范规程设计(图4)，抗震设防烈度为7度，设计基本地震加速度值为0.10g。

图4 10层框架结构示意图Fig.4 Schematic diagram of a 10-story frame structure

考虑到多自由度模型较好的非线性特性表示能力与较高的计算效率[31]，将质量凝聚在各楼层建立结构的串联10自由度非线性模型。采用Takeda三线性恢复力曲线以准确地表示结构的层间行为[32 − 33]。结构与恢复力模型参数如表2所示，一阶自振周期为0.7533 s。

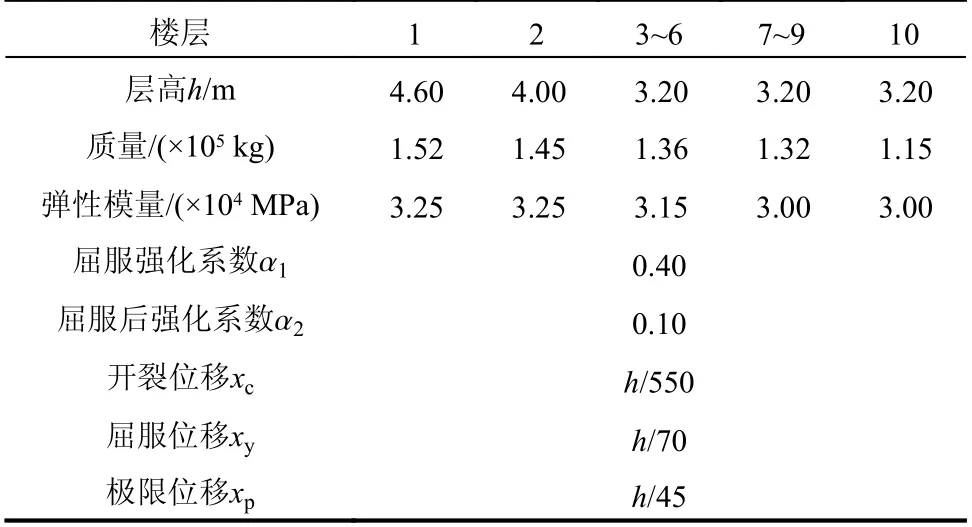
表2 10层框架结构参数与恢复力模型Table 2 Parameters and restoring force model of a 10-story frame structure

从太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center, PEER)[34]选取了c类场地的57条地震动加速度时程(不区分方向)并进行基线修正，采样间隔均为0.01 s。将27条东日本地震动作为训练数据，30条不同地区的地震动作为测试数据，详细信息如表3所示。值得注意的是，为了验证LSTM的泛化能力，保留了不同地区地震动间的频谱差异。

表3 地震动数据集Table 3 Earthquake ground motion dataset

在本例中，滑动窗口大小设置为50，所有地震动被调幅为2.5 m/s2以保证相近的非线性程度。采用数值积分法计算结构在每条地震动作用下的非线性动力响应，输出1层、5层、9层的位移时程，并对结果进行间隔为0.07 s的下采样。经过时间窗划分，训练集包含114 291条数据，测试集包含15 629条数据。

建立结构对应的LSTM神经网络模型并进行训练。训练过程包含1500次迭代，每次迭代训练100个小批量，每个批量大小为256，均方误差损失函数的变化趋势如图5所示。迭代1302次时，测试集损失达到最低，此时执行早停操作。利用训练好的LSTM模型对测试集中的结构响应进行预测。

图5 损失函数变化趋势Fig.5 Tendency of loss function

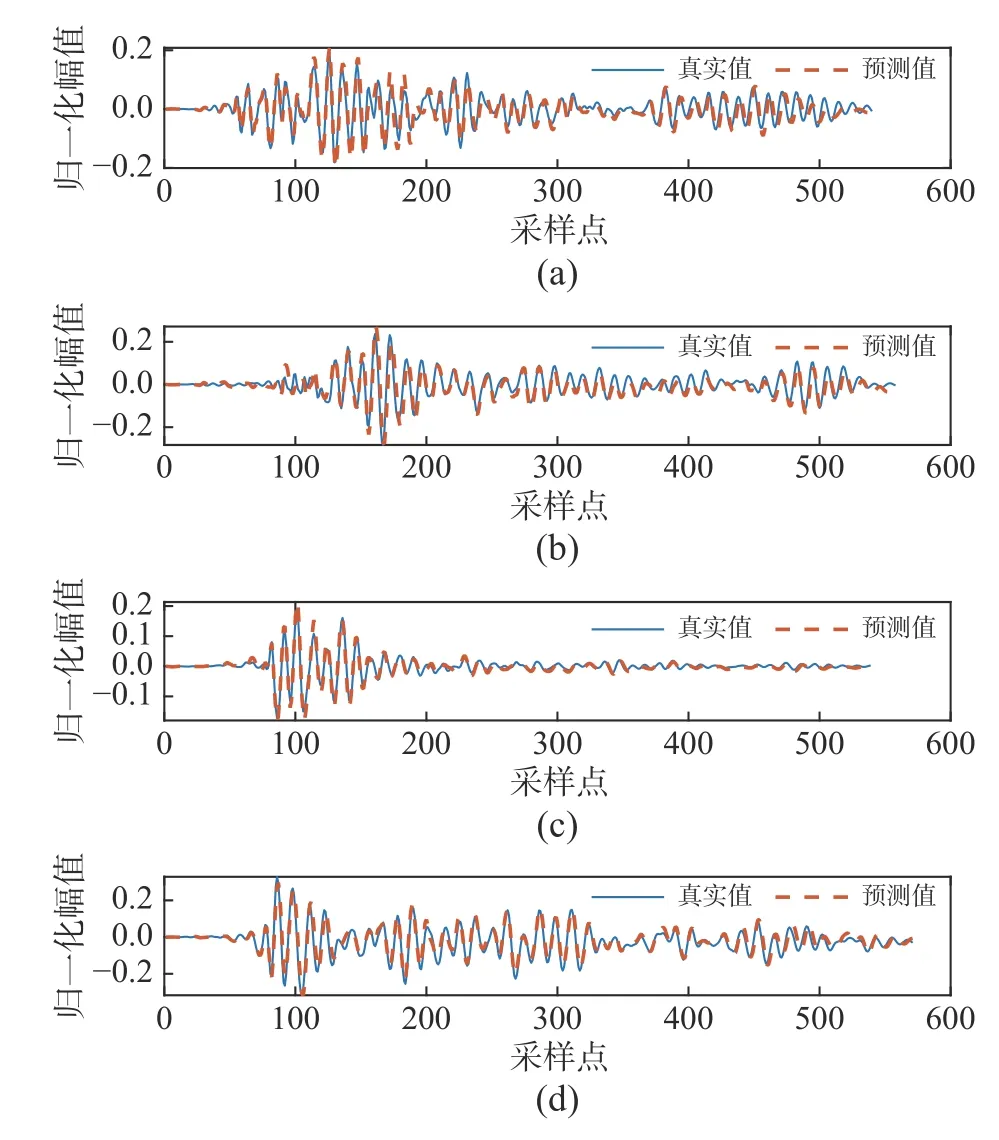
图6 例1中4条地震动响应时程的预测结果Fig.6 Four prediction results of the seismic response time history in Example 1

3.2 例2. 6层框架结构

神经网络方法由于数据驱动的特点，其直接信息来源为结构响应，而非传统求解方法的地震动与结构特性。因此LSTM对结构响应时程自身的特性更加敏感，并对结构特性等因素具有内在的泛化能力。响应的时频域表现是响应时程的关键特性，因此有必要使用具有不同主周期的结构响应验证LSTM神经网络模型的预测能力。

对于某6层剪切型框架办公楼，其抗震设防标准与3.1节相同，将质量凝聚在各楼层建立结构的串联6自由度非线性模型。该模型使用了不同的恢复力特性曲线，其结构与恢复力模型参数如表4所示，一阶自振周期为0.4794 s。与3.1节相比，使用了相同的地震动时程生成训练集与测试集，但将滑动窗口大小设置为100，幅值调整为4 m/s2，采样间隔为0.05 s。经过时间窗划分，训练集包含159 246条数据，测试集包含21 014条数据。建立结构对应的LSTM神经网络模型并进行训练。训练过程包含2385次迭代，其他参数与3.1节相同。

表4 6层框架结构参数与恢复力模型Table 4 Parameters and restoring force model of a 6-story frame structure

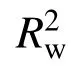
图7 例2中4条地震动响应时程的预测结果Fig.7 Four prediction results of the seismic response time history in Example 2

4 模型参数选取原则

前述研究表明了LSTM方法预测结构非线性地震响应的可行性。在实际应用中，应通过调节窗口大小与数据集采样间隔来调控输入模型的信息量以获得最优的预测效果。其中，窗口大小控制了信息长度，以适应不同的地震动幅值；采样间隔控制了信息密度，以适应不同的建筑结构。本节对上述关系进行了详细的讨论，并给出了相应的参数选取原则。

4.1 窗口大小的选取

窗口大小是LSTM神经网络模型在预测阶段的唯一可调整参数。窗口大小表示模型在递推预测中的输入时间序列长度，对预测结果具有显著影响。直观地分析，更小的窗口会因为更多的训练数据和更快的训练速度而提高训练效率，但模型更难从短时间序列中提取到有效信息，降低了预测的准确度。更大的窗口会导致训练数据减少和训练速度降低，且同样会降低预测的准确度。

训练中还发现，当窗口大小超过一定的容忍范围后，预测误差会随递推次数增加而累计，导致预测结果的发散，如图8所示。发散现象常常出现在响应幅值较小处，可能与输入序列的约束减弱有关。因此，需要选取合适的窗口大小以实现训练效率和准确度的平衡。经过反复尝试，发现窗口大小在(50，100)范围内可以取得相对合理的结果，且具体数值可依据输入地震动的峰值加速度(PGA)与结构抗震设防烈度的关系来选取。

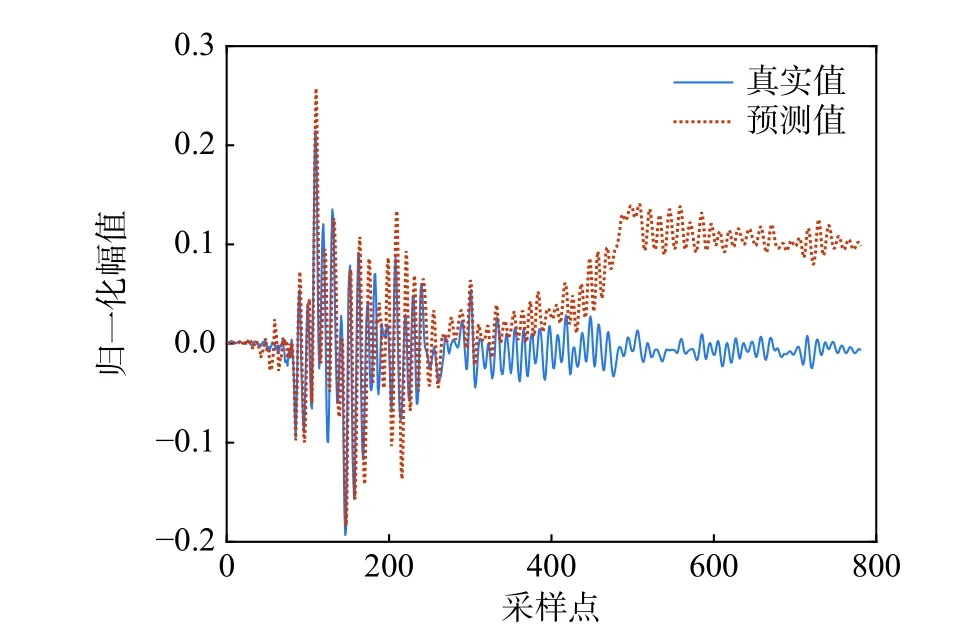
图8 某地震动时程出现的发散现象Fig.8 The divergence of a certain earthquake time history

为了对此建议范围进行验证，训练了例1结构的8个具有不同训练集和窗口大小的LSTM神经网络模型。命名方式记为M{训练集编号}-{窗口大小}，如M1-50代表使用train1训练集，窗口大小为50的模型。

训练集与测试集的选取与第3节相同，但对地震动进行了不同等级的峰值加速度调幅以模拟不同的非线性水平。对于本文使用的7度抗震设防结构，第一组训练集调幅为2.5 m /s2，模拟高于设防烈度的罕遇地震烈度(8度，0.20g)水平，记为train1。第二组训练集调幅为4 m/s2，模拟远高于设防烈度的极罕遇地震烈度(9度，0.40g)水平，记为train2。相应的，两组测试集分别记为test1、test2。

表5记录了所有模型的基本信息及其在不同测试集上的评价结果，指标数值取为测试集地震动预测结果的均值。

由表5可以看出：

表5 窗口大小取值分析的模型评价结果Table 5 Model evaluation results of window size analysis

1) 对同一组目标地震动，PGA决定了最优预测精度：更小的PGA对应更好的预测结果。相同条件下，M1模型的评价指标均优于M2模型。这是因为一方面随着PGA提高，响应的非线性发展更加充分，进入屈服段的历程也随之增加，神经网络更难以学习更复杂的滞回关系。另一方面，神经网络难以捕捉到时程后半段出现的塑性(残余)位移量，从而引起WRMSE指标的增加。尽管如此，在M2-100模型上，加权决定系数指标依然保持在0.7以上，且后半段的弹性位移量得到了精确的还原，反映出良好的整体拟合能力。

2) 对同一结构，各层的预测精度相似，具有相近的评价指标。此外观察到有量纲指标WRMSE会随层数增加而增大，这是由各层位移幅值的量级不同决定的。

3) 窗口大小取值(50，100)较为合理。M1模型在窗口大小取25、125时的评价指标明显劣于建议范围内的指标。通过观察时程可以发现，M1-125模型的误差主要来源于时程整体的欠拟合，M1-25模型的误差则主要来源于时程后半段的发散现象，这与上文的分析相符。

4) 模型的最适窗口大小与PGA和结构抗震设防烈度的关系有关：PGA满足高于设防烈度的罕遇地震烈度水平时，窗口大小应选取50附近的较小值；PGA满足高于设防烈度的极罕遇地震烈度水平时，窗口大小应选取100附近的较大值。M1模型对应于罕遇地震烈度，最适窗口大小为50。M2模型对应于极罕遇地震烈度，最适窗口大小为100。这是由于在更大的PGA下，结构更容易处于屈服后的强化阶段，响应的主频率更低，波形更长。而神经网络预测是输入形状特征与物理机制共同作用的结果，因此需要增加窗口大小以获取足够的输入信息。

4.2 数据集采样间隔的选取

现代地震动观测仪器的采样间隔一般低于0.01 s，因此一条完整的地震动时程可能包含几千到数万个采样点。对于LSTM神经网络，使用原始时间间隔的地震动记录进行训练意味着巨大的参数量与计算成本。因此为了尽可能地减少训练时间，提高输入序列中的“信息密度”，需要对地震动及其响应时程进行下采样。

对于不同结构的响应时程预测，应采用不同的下采样间隔。采样间隔 Δt的选取需要满足以下两个原则：1) 减少下采样造成的峰值响应损失，即采样间隔小值优先；2) 采样间隔应与建筑结构自身特性有关，即结构的自振周期越大，响应振动的波长越大，需要的采样间隔越大。采样间隔Δt的选取可表示为：

式中，T1表示结构的基本周期。

为了验证其合理性，对两个结构在不同数据集下的结构响应时程进行了傅里叶变换并计算其平均主周期，结果如表6所示。观察发现地震动幅值与结构特性均对响应时程的波长具有明显影响。对于地震动数据集，随着PGA增大，响应时程主周期(或波长)小幅增加，这与4.1节的分析相符。对于结构特性，结构基本周期与线性响应时程主周期基本相同，由此可以证明结构的基本周期可以作为响应时程采样间隔的控制因素。第3节中两个框架结构的基本周期分别为0.7533 s、0.4794 s，相应的采样间隔分别为0.07 s、0.05 s，满足式(13)且与小值优先的原则相符。

表6 不同地震动与结构的响应主周期Table 6 Response main period under different ground motions and structures

5 模型泛化能力分析

结构的地震响应主要受到结构自身动力特性与地震动特性两个因素影响[35 − 36]。为验证LSTM网络模型在不同工况下的泛化能力，本节设计了例1、例2结构下使用不同训练集、测试集的对比试验，并给出了不同指标下的评价结果。

5.1 地震动泛化能力分析

5.1.1 地震动频谱特性

地震动频谱特性显示了不同频率分量的强度的分布，反映了地震动的动力特征。对于不同频谱特性的地震动，其响应预测性能可能也会有所不同。选取了4.1节中的M1-50模型进行测试，并依据评价指标WRMSE和加权决定系数对30条测试集地震动的预测结果进行了汇总，如图9所示(左图为按指标数值升序排序后的分布，右图直方图分布)。

图9 M1-50模型的测试集预测结果分布Fig.9 Distribution of prediction results of the test set of the M1-50 model

在30条测试集地震动中，WRMSE指标最低的3条地震动编号为25、17、0，最高的3条地震动编号为18、16、15，对应地震动的傅里叶幅值谱与加速度时程如图10所示。

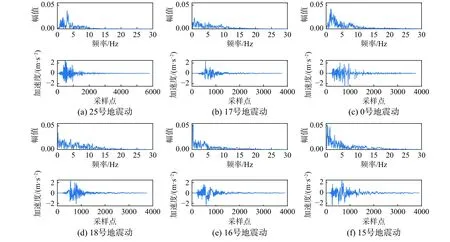
图10 代表性地震动的傅里叶幅值谱与加速度时程Fig.10 Fourier amplitude spectrum and acceleration time history of representative ground motions

对两组结果进行对比：在频域上，第一组地震动相比第二组具有较少的低频(低于1 Hz)成分，呈现出典型的地震动频谱分布特征。在时域上，第二组地震动由于幅值与频率变化表现出的非线性更加明显。此外，发现训练集地震动的频谱特征与第一组地震动更为吻合，由此可以从数据不平衡分布的角度解释不同地震动间预测性能的差异，同时可以认为：

2) 频谱分布对神经网络预测结果有重要影响。整体而言，训练与测试地震动频谱分布的差异反映在训练数据分布的不平衡上。非典型频谱分布地震动样本远远少于典型样本，难以被神经网络充分学习，从而造成预测结果准确性偏低。

3) 低频段频谱分布是最为明显的影响因素。具体而言，低频段幅值越高，地震动在时程上越容易出现造成局部幅值偏移的低频波，增加了非线性变化的复杂程度和预测难度。?

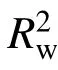
图11 滤波前后16号地震动预测结果对比Fig.11 Comparison of prediction results of No. 16 ground motion before and after filtering

5.1.2 地震动幅值

在模型的实际应用中，预测目标地震动可能并不局限于同一PGA，而是根据抗震设防等级进行不同程度的调幅，因此需要考虑模型在非目标峰值地震动上的预测性能。

训练集与测试集的选取与第3节相同，但对地震动进行了不同等级的峰值加速度调幅。第一组训练集调幅为2.5 m/s2，记为train1。第二组训练集调幅为4 m /s2，记为train2。将前两组训练集合并得到复合训练集，记为train3。同理，调幅得到了测试集test1、test2。

表7记录了4个LSTM神经网络模型的基本信息及其在不同测试集上的评价结果。采用的指标包括WRMSE、Pearson相关系数、R2w和峰值百分误差，指标数值取为测试集所有地震动结果的均值。

表7 地震动泛化能力分析的模型评价结果Table 7 Model evaluation results of earthquake generalization ability analysis

由表7可以看出：

1) LSTM神经网络对地震动幅值的变异具有良好的泛化能力。当窗口大小合适时，对非目标峰值地震动进行预测仍然可以得到相对优秀的结果，如M1-100在test2上仍然具有0.7707的加权决定系数，优于M2-100。这可能是由于train2训练集中的响应具有更大的塑性位移，干扰了模型对滞回特征的学习。

2) 目标地震动峰值水平较高时，使用不同幅值的复合训练集可以得到更优秀的模型。M3-100相比M2-100在test2的各个指标上都得到了一定程度的提高，尤其是WRMSE和峰值百分误差分别为0.0126 m、11.31%，达到了所有模型中的最优水平。这是因为复合训练集增加了数据量，减少了训练中的过拟合，使训练损失得以下降至更低。

3) 通常情况下，可以考虑使用峰值水平较低的训练集进行训练。一方面，低峰值水平响应的塑性位移通常更小，即误差干扰更小，模型更容易学习到结构的滞回特性。另一方面，调试和训练时间相比复合训练集更短，易于应用。