基于醉汉漫步和反向学习的灰狼优化算法*

刘 炼,付绍昌,黄辉先

(湘潭大学自动化与电子信息学院,湖南 湘潭 411105)

1 引言

高维函数优化问题在理论研究和实际生产过程中具有很重要的应用价值，许多问题可通过数学建模转换为最优问题，如物流配送路径优化的研究[1]、高铁动态调度方法问题[2]和多分类孪生支持向量机参数优化问题[3]。高维复杂函数优化通常是指维度超过100维的函数优化问题，而随着维度的增加，问题的局部最优值也会增加，其计算复杂度也会呈指数级增长[4]，解决问题的难度也随之加大。

近年来随着群体智能SI(Swarm Intelligence)算法的兴起，遗传算法GA(Genetic Algorithm)、粒子群优化PSO( Particle Swarm Optimization)算法和人工蜂群ABC(Artificial Bee Colony)算法等相继被提出。郭佳等[5]提出一种优化的马尔可夫链人工蜂群算法，通过马尔可夫链对第一阶段产生的解空间进行重构，减少了人工蜂群算法的随机性，同时避免了因依赖某一最优值导致的算法早熟。冯璋等[6]提出一种二维主成分分析法与主成分分析法结合与改进灰狼优化算法共同优化支持向量机的人脸识别方法，以减少提取特征的维度和提取时间,从而缩短了支持向量机所需的识别时间，为了提高灰狼优化算法的全局搜索能力,引用精英反向学习策略初始化种群。在光伏大规模故障系统中，标记数难以记录，Huang等[7]提出了一种结合人工蜂群算法和半监督极限学习机的新算法来解决该问题。随着社会的进步，问题复杂程度不断增加，为进一步检测算法的综合能力，近几年研究人员提出了更复杂的测试函数，如CEC(Congress on Evolutionary Computation)2013、CEC2014等。以上学者所提出的改进算法无论在全局收敛性还是求解精度方面都待提高，同时算法寻优只针对标准测试函数，对复杂测试函数效果不佳。

灰狼优化GWO(Grey Wolf Optimizer)算法是Mirjalili等[8]在2014 年提出的一种群体智能优化算法。GWO概念清晰，具有结构简单、计算时间复杂度低、易于实现和局部寻优能力强等特性，拥有良好的全局搜索和局部搜索切换机制，得到了诸多国内外研究者的认可。Teng等[9]提出了一种结合粒子群优化算法的灰狼优化算法PSO_GWO，利用非线性控制参数来平衡算法的搜索能力，提高算法的收敛速度。Pan等[10]将种群狼分成几个独立的群体，提出了一种并行灰狼优化算法。Mittal等[11]通过控制参数a协调算法的探索和开发能力,提出了一种改进的灰狼优化算法MGWO(Modified GWO)。柳长安等[12]设计了一种静态平均和动态加权平均混合的位置更新策略，并使用非线性递减函数改进灰狼优化算法距离控制参数。GWO 算法虽然得到了许多改进,但针对高维复杂函数问题的研究仍不多见。龙文等[13,14]对高维复杂函数优化问题进行了研究，但其收敛精度不是很高，且在近几年提出的复杂测试函数上效果不明显。为增强算法综合寻优能力，同时兼顾对标准测试函数和复杂测试函数的寻优效果，本文将醉汉漫步、反向学习与灰狼优化算法相结合，提出一种改进灰狼优化算法DGWO(Drunkard Grey Wolf Optimizer)。算法主要改进策略为：

(1)为增加局部搜索和全局搜索能力，对种群中精英个体采用醉汉漫步策略进行更新。

(2)为避免陷入局部最优，对种群中α、β、δ与当前种群中适应度值最差的3匹狼进行反向学习，重新计算适应度值并与本身比较排序，将3匹最好的狼随机保留在狼群中，以增加种群多样性，增加跳出局部最优的概率。

(3)为平衡局部搜索能力和全局搜索能力，种群迭代过程中，更新时参数A、C采用标量系数[15]和矢量系数，各为迭代次数的一半。

实验测试，该改进算法应用于高维测试函数与复杂函数时在精度和收敛速度上有明显的优势，可应用于两级运算放大器参数设计中。

2 基本灰狼优化算法

GWO算法是受大自然中狼群狩猎捕食的启发而提出来的，其中α狼为当代种群中最靠近猎物的狼，β狼和δ狼为第2和第3靠近猎物的狼，ω狼则为种群中其它狼。在狼群搜捕猎物时ω狼受α、β、δ狼的引导朝3匹狼的方向前进，以实时更新自身的位置，并靠近猎物。根据狼群狩猎时所建立的数学模型如式(1)～式(4)所示：

X(t+1)=Xp(t)-A·D

(1)

A=2·a·r1-a

(2)

D=|C·Xp(t)-X(t)|

(3)

C=2·r2

(4)

其中，t为当前迭代次数;Xp(t)为猎物位置;A为收敛因子，其值控制着ω狼是接近还是逃离领导狼，当A的绝对值大于1时狼群将逃离领导狼，此时ω狼会放弃此时可能有猎物的区域，去探索更多的区域；D为包围步长；r1和r2是随机向量，其分量取值为[0,1];a随着整个迭代过程的进行从2到0逐渐线性减小,a={a,a,…,a}是由a构造出的向量，其维度与r1维度相同;C为摆动因子。

狼群个体在包围猎物时的数学模型如式(5)～式(11)所示，式(5)～式(10)用于计算狼群个体与α、β、δ狼的距离，式(11)用于计算新的狼群个体位置:

Dα=|C1·Xα-X(t)|

(5)

Dβ=|C2·Xβ-X(t)|

(6)

Dδ=|C3·Xδ-X(t)|

(7)

X1(t)=Xα-A1×Dα

(8)

X2(t)=Xβ-A2×Dβ

(9)

X3(t)=Xδ-A3×Dδ

(10)

X(t+1)=[X1(t)+X2(t)+X3(t)]/3

(11)

其中，Xα、Xβ和Xδ分别表示α、β和δ的位置，Dα、Dβ和Dδ分别表示狼群个体到α、β和δ的距离，A1～A3，C1～C3分别表示通过式(2)和式(4)生成的随机数。

基本GWO 算法的伪代码如算法1 所示。

算法1基本GWO算法

输入：种群规模N，迭代次数t，最大迭代次数Maxit。

输出：Xα。

1：在搜索空间中随机生成N匹初始狼；

2：根据式(3)和式(4)计算参数A、a和C的值;

3：依次计算适应度值f(Xi),i=1,2,3,…,N;

4：将狼按适应度值升序排序，取前3分别标记为Xα、Xβ和Xδ，令并t=0;

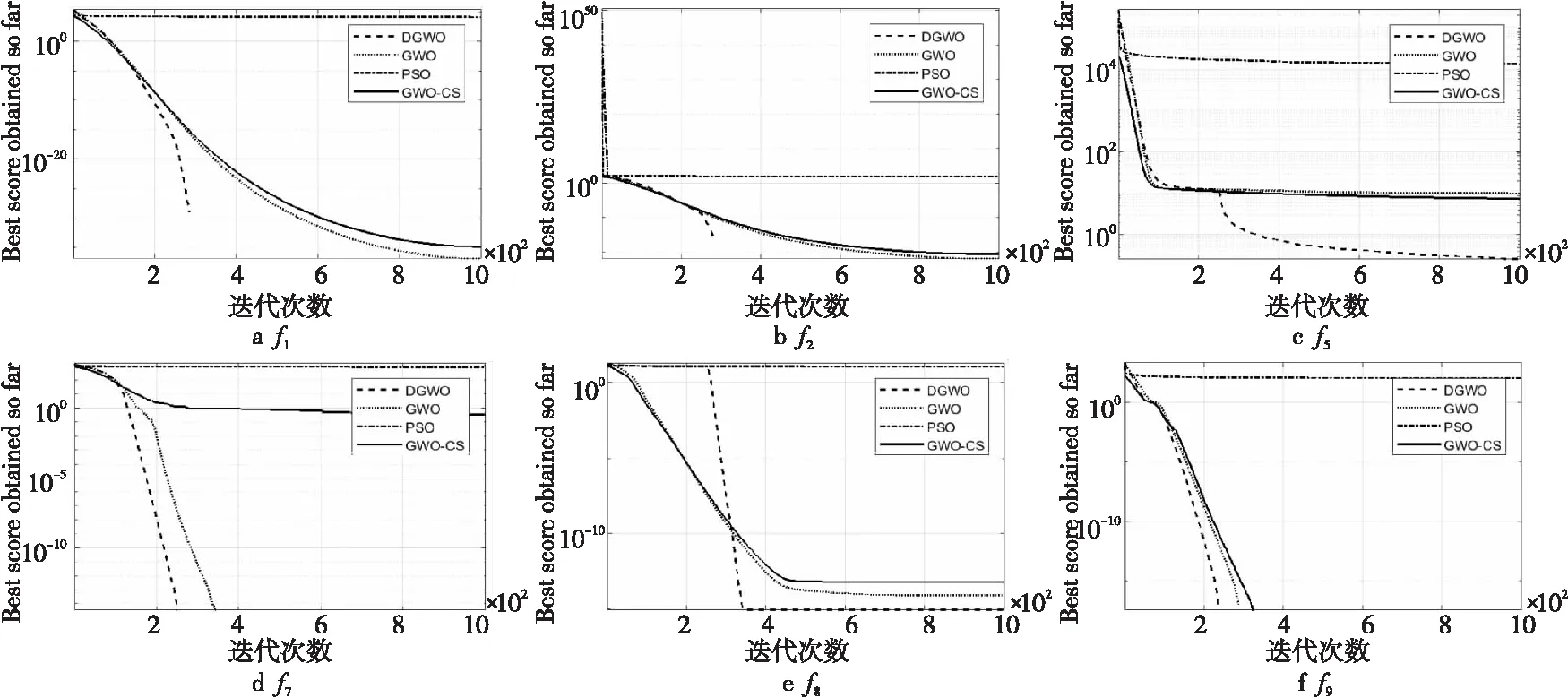
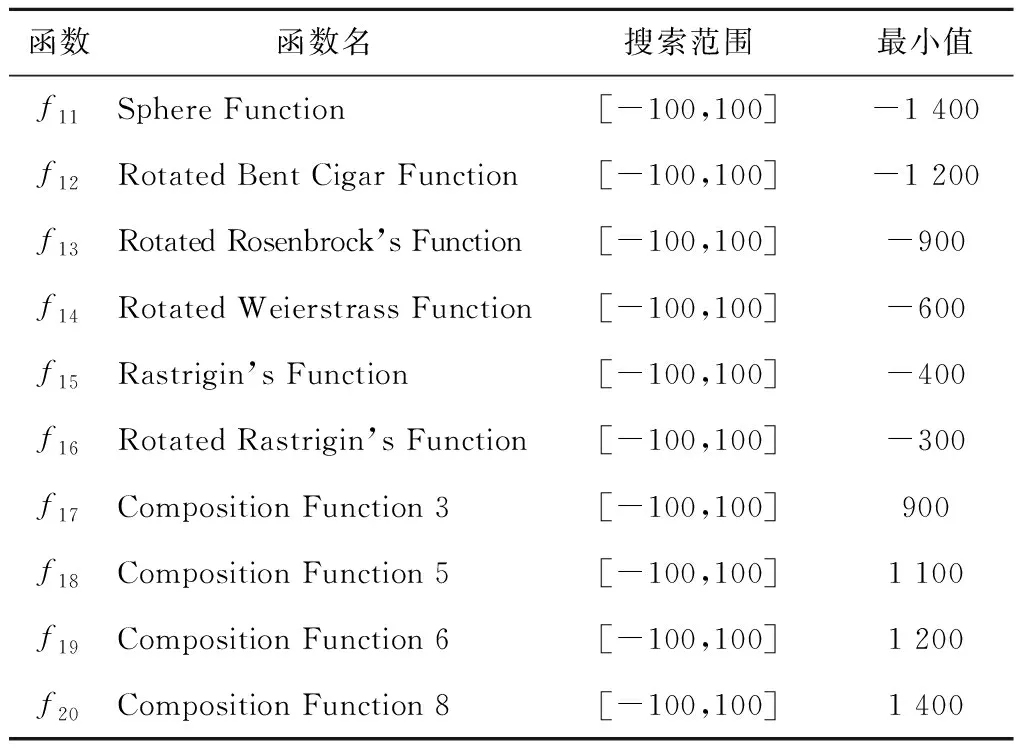
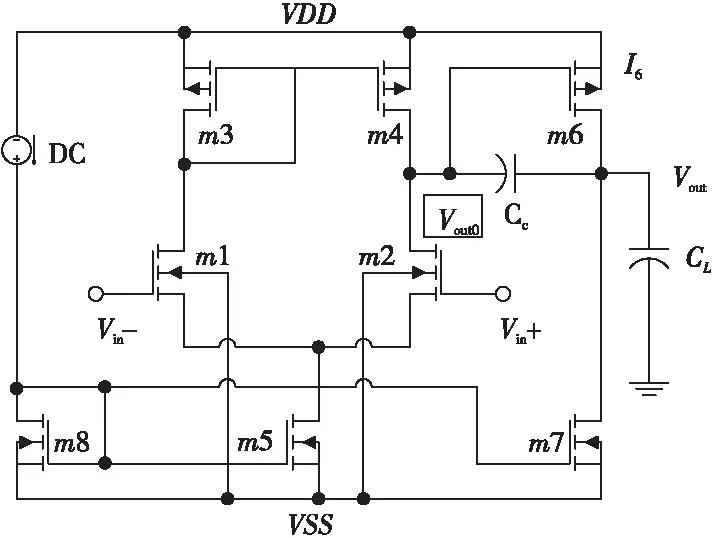
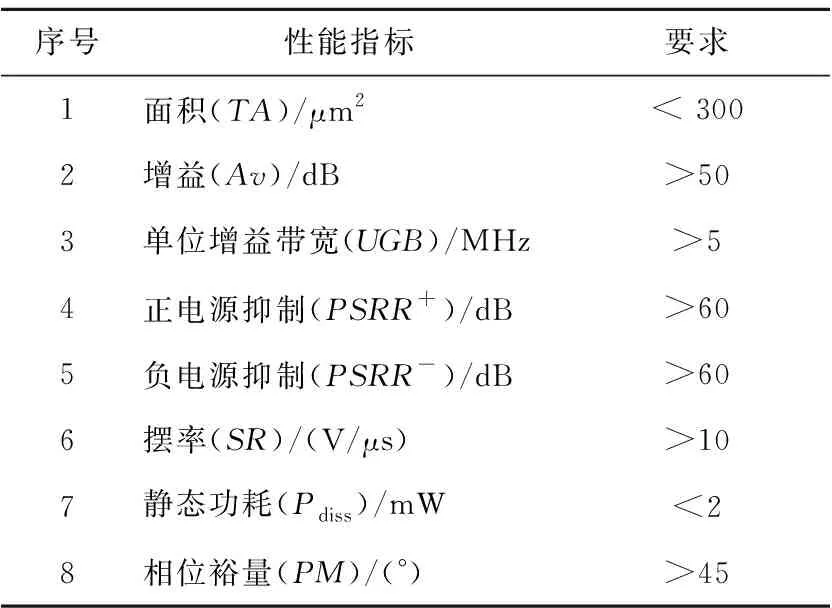
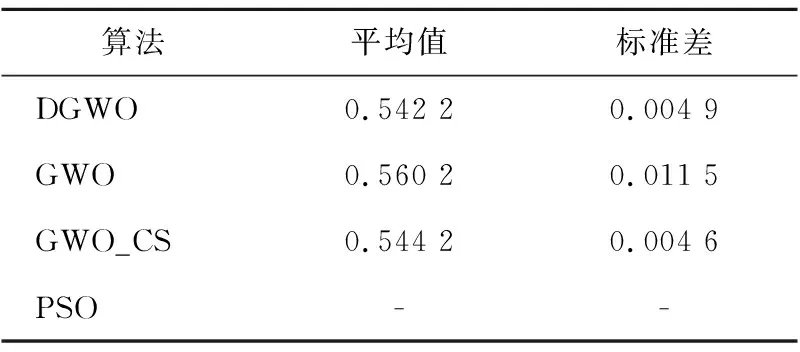
5：whilet

6：fori=1 toNdo

7： 根据式(8)～式(11)更新第i匹灰狼的位置;

8：endfor

9： 根据式(3)和式(4)更新参数A和C的值;

10： 重新计算适应度值f(Xi),i=1,2,3,…,N;

11： 更新Xα、Xβ和Xδ的值;

12：t=t+1;

13：endwhile

14:returnXα

3 改进的灰狼优化算法DGWO

3.1 醉汉漫步模型

随机漫步(Random Walk)[16]思想最早由Pearson在1905年提出的，它是一种不规则的变动形式，变动过程中的每一步都是随机的。随机漫步的思想是,从随机点出发进行随机跳跃但会遍历整个图。随机漫步已在众多领域得到应用。Gupta等[17]提出一种新颖的随机漫步灰狼优化算法，并证明可解决连续优化问题，而且可以解决实际生活优化问题。随机漫步可大致分为3种：马尔可夫链[18]、醉汉走路(Drunkard Walk)[19]和莱维飞行(Lévy Flight)[20]。本文采用基本的醉汉漫步模型，该模型在初始化时产生一组随机数，如式(12)所示：

Di=(r3*2-1)*π

(12)

其中,r3∈[0,1]，π为圆周率。

如式(13)～式(17)所示进行三角变换：

newx=step×sin(Di)+oldx

(13)

Drβ=newx·(Xβ-Xα)

(14)

Drδ=newx·(Xδ-Xα)

(15)

X(t+1)=a×Drβ+Xβ

(16)

oldx=newx

(17)

X(t+1)=a×Di+Xα

(18)

其中,step为醉汉步长，步长可固定也可变化，小步长促使在当前子代附近展开搜索，而足够大的步长有助于探索新的有希望或未探索的搜索区域，本文中step固定为2。

本文根据式(13)～式(17)更新β狼和δ狼。根据式(18)更新α狼，醉汉漫步具有强大的随机性，方向具有不确定性，精英狼处于当前狼群最优位置，故精英狼漫步增强了精英狼的局部搜索能力，在优化复杂函数时效果明显。

3.2 反向学习策略

反向学习策略[21]是由Tizhoosh于2005 年提出的一种智能计算方法，广泛应用于各种算法优化中，以提高算法搜索性能。利用反向学习策略的有效性，张新明等[22]提出一种最优最差反向学习策略，实验结果表明最优最差反向学习策略比一般反向学习策略更有效。反向学习的主要思想是在同一空间中对当前解进行反向求解，设xj是某一对象n维空间的一个当前解，x*为反向解，则x*通过式(19)进行求解,且x1,x2,…,xn∈R，xj∈(aj,bj),aj与bj分别代表搜索空间上下限。

x*=aj+bj-xj

(19)

狼群中α、β、δ狼与最差的狼的信息是当前狼群所积累的知识和经验的代表。在本文改进的灰狼优化算法DGWO中，α、β、δ狼均为精英个体，在求α、β、δ狼的反向解的同时将狼群中适应度最差的3匹狼进行反向求解，并重新计算6个反向解的适应度值且进行排序，用排序后前3的反向解随机替换种群中的个体，以增加种群的多样性，扩大搜索范围。为了协调算法的勘探和开采能力, 引入反向学习策略。由精英反向学习策略可知, 将反向解与当前解同时保留，可增强下一代群体中种群的多样性, 能增加算法跳出局部最优的概率；另一方面,反向解又保留了当前种群中精英个体的有益搜索信息，可以加快算法的收敛速度。

3.3 算法步骤

综上所述,改进灰狼优化(DGWO) 算法的步骤如下所示：

步骤1算法参数设置：种群规模N，最大迭代次数Maxit。

步骤2随机生成初始种群，计算每个个体的适应度值并排序，将前3个最优个体的位置依次保存为Xα、Xβ、Xδ。

步骤3根据式(5)～式(11)更新灰狼位置信息,更新A，a，C的值。

步骤4根据式(12)～式(18)更新α、β、δ狼。

步骤5根据式(19) 进行反向学习。

步骤6重复步骤3～步骤5直到达到最大迭代次数，输出α狼位置，算法终止。

4 实验及数值分析

4.1 测试函数

本节采用国际通用的10个标准测试函数验证本文DGWO算法的有效性，并将其应用于模拟集成电路参数设计问题。为了验证该改进算法求解高维函数的有效性，本文还选取了10个高维测试函数进行实验，并将测试结果与PSO、GWO-CS和GWO的测试结果进行对比。10个标准测试函数如表1所示，表中n表示维度，Fmin表示全局最优解的值。

4.2 基本GWO算法与DGWO算法对比

为了保证公平性，算法进行对比时采用相同的参数初始化设置，其中求解高维测试函数时种群规模N=50，最大迭代次数Maxit=1000。在GWO中，参数a的初始值为2。每种算法独立运行30 次，记录寻优的最优值、最优值位置、平均值以及标准差。所有测试均在Intel(R) Core(TM)i5-4590 CPU、6 GB内存、3.30 GHz的计算机上进行，利用Matlab 2017a编写程序。采用DGWO对表1中10个测试函数进行求解，并与基本GWO进行对比。

Table 1 10 standard test functions表1 10个标准测试函数

由表2可看到，改进后DGWO算法与基本GWO算法相比有明显改进，其中f1、f2、f3、f4、f5、f7、f8、f9的收敛精度有了明显提高，且寻到了f1、f2、f3、f7、f8、f9的全局最优解，标准差达到零，其仿真结果显示了DGWO算法改进策略的有效性。

表3给出了DGWO与3种对比算法(PSO、GWO和GWO-CS)对表1中10个可变维测试函数在100维、500维和1 000维中各自的寻优结果对比,其中种群规模N=30,最大迭代次数Maxit=500,算法独立运行20次。通过分析表3可以得知全部测试函数取得最优值，在100维、500维和1 000维的情况下函数f1、f2、f3、f7、f9均达到理论最小值0，函数f8达到理论最小值8.88e-16。

Table 2 Results comparison of 10 standard test functions between GWO algorithm and DGWO algorithm表2 GWO算法与DGWO算法对10个标准测试函数结果对比

Table 3 Optimization results of PSO,GWO,GWO-CS,DGWO algorithms on high-dimensional function 表3 PSO、GWO、GWO-CS、DGWO 在高维测试函数上的寻优结果

在其它函数的寻优精度上，与3个对比算法相比均具有优势。随着维度的增大，3种算法的寻优精度明显下降，但本文DGWO算法在测试函数寻优结果中均具有优势，且标准差同样具有优势。总体来说,本文提出的DGWO算法在100维、500维、1 000维的测试函数上相对于GWO、PSO和GWO-CS算法寻优结果更优。

由表3可知，DGWO与GWO、PSO、GWO-CS相比在100维、500维以及1 000维时均取得了较优的结果，PSO算法均未收敛，GWO在100维时(f1、f2、f3、f6、f7和f8)收敛，在500维和1 000维时只有部分收敛，由此可见GWO算法在高维函数寻优方面还有提升空间。

为了更直观地比较4种算法的收敛精度与收敛速度，图1给出函数f1、f2、f5、f7、f8、f9的适应度进化曲线图进行对比。从图1中可看出，与PSO、GWO、GWO-CS算法相比，DGWO算法寻优效果更好，精度更高，收敛速度也快。

从图1中f2、f5、f8的适应度进化曲线可以看出，在迭代过程中算法收敛速度较快，体现出改进算法在陷入局部最优时具有良好的机制跳出局部最优，找到全局最优解。

为进一步验证本文提出的改进算法的有效性，本文使用10个CEC2013[23]测试函数作为寻优对象，测试函数中包含单峰函数(f11、f12)、多峰函数(f13～f16)及组合函数(f17～f20)。各算法寻优参数设定如下：维度为10，种群规模N=50，最大迭代次数Maxit=1000，算法独立运行30次，测试函数如表4所示，寻优结果如表5所示。

Figure 1 Fitness curves of 4 algorithms on 6 functions图1 4种算法在6个标准测试函数上的适应度进化曲线

Table 4 CEC2013 test functions

由表5可知,与GWO、PSO、GWO-CS相比，DGWO在f11～f20上均具有优势，平均值均取得最优，大部分标准差取得最优。在单峰函数(f11)上取得全局优解，且标准差较小，可以看出该改进算法在复杂单峰函数上较对比算法具有明显优势，在多峰函数(f13～f16)上均取得最优，对于函数f13和f16改进效果显著，明显提高了收敛精度，在组合函数(f17～f20)上测试算法性能时，DGWO同样均取得最优，且相较于GWO、PSO和GWO-CS具有明显的效果，f17、f19、f20平均值有大幅度提高。由以上的比较结果可知，DGWO在求解大部分函数时具有优势，不仅仅在高维测试标准函数上，而且在复杂测试函数上同样具有优势，进一步验证了DGWO算法的有效性。

4.3 计算复杂度

评价元启发式算法有效性的一个指标为计算时间复杂度。计算时间复杂度越低的算法，可以用越少的计算力来完成相同的求解任务。在最坏的情况下，DGWO与GWO、GWO-CS的计算时间复杂度如下所示：

在初始化阶段，DGWO与GWO、GWO-CS的时间复杂度相同。种群初始化时的时间复杂度为O(N),其中N为种群大小。参数a、A和C的初始化时间复杂度为O(3)，领导者的产生过程的时间复杂度为O(3N)。

Table 5 Optimization results of 4 algorithms on CEC201310 test functions表5 4种算法在CEC201310测试函数上的寻优结果

每种算法的主要计算步骤都在 while 循环中。在 GWO中，种群位置更新的时间复杂度为O(N)；在假设每个测试函数的时间复杂度为O(1)的前提下，种群适应度计算的时间复杂度为O(N)；参数更新、领导者更新过程的时间复杂度分别为O(3)和O(3N)。综上所述，while 循环的时间复杂度为O((5N+3)·T)，其中T是最大迭代次数。GWO 的总计算时间复杂度为O(T·N)。

在GWO_CS中种群位置更新的时间复杂度为O(N)；杜鹃搜索复杂度为O(3N)，种群重新更新计算复杂度为O(N)。部分参数更新计算复杂度为O(10)，领导者更新过程的时间复杂度为O(3N)。综上所述，while 循环的时间复杂度为O((8N+10)·T)，其中T是 最大迭代次数。GWO_CS 的总计算时间复杂度为O(T·N)。

因此，考虑最坏情况下，3种灰狼优化算法的计算时间复杂度相同。

5 在两级运算放大器设计中的应用

随着模拟集成电路(IC)的拓扑结构变得越来越复杂，模拟电路设计自动化面临更多更严峻的挑战。模拟集成电路的参数设计可以通过建立数学模型转化为一个优化问题，在保证增益、转换速率、单位增益和带宽等设计指标的前提下获得最优解，大大缩短设计时间，提高电路的综合性能。本文以L50G CMOS工艺下两级无缓冲运算放大器的增益优化设计为例[24,25]检验DGWO算法的实用性。该放大器的电路如图2所示。

Figure 2 Standard two-stage operational amplifier图2 标准两级运算放大器

该问题的数学模型如下所示：

considerX=[x1,x2,…,x10]=[S1,…,S8,I6,Cc]

minf(X)=EAv/Av=EAv/(20 lg(2gm1gm6/(x9I6(λ2+λ4)(λ6+λ7))))

s.tg1(X)=EUGB/UGB=EUGB/(gm1/(x10+A2Cgd6))≤1

g2(X)=ESR/SR=ESR/(x9/x10)≤1

g4(X)=EPSRR+/PSRR+=EPSRR+/(20 lg(2gm1gm6/(x9λ6I6(λ2+λ4))))≤1

g5(X)=EPSRR-/PSSR-=EPSRR-/(20 lg(2gm1gm6/(x9λ7I6(λ2+λ4))))≤1

g6(X)=Pdiss/EPdiss=(VDD-VSS)(2x9+

I6)/1000/EPdiss≤1

g7(X)=10gm2/gm6≤1

g8(X)=0.122CL/x10≤1

g9(X)=10UGB/P3≤1

h1(X)=x1-x2=0,h2(X)=x3-x4=0

wheregm1=gm2= (K′nx1x9)0.5

gm3=gm4= (K′px3x9)0.5

gm6=gm4x6/x4

A2=gm6/(I6(λ6+λ7))

Cgd6=CGDOP·x6·L

P3=gm3/(4/3·COXx3L2)

Rangex1,x2,…,x8∈[1,50],x9∈(0,30],x10∈(0,10]

其中，λ2,λ4，λ6和λ7分别代表晶体管m2,m4,m6和m7的沟道调制系数。

在DGWO的基础上，引入非平稳多级分配罚函数约束处理方法[26]对模拟电路进行优化设计。

表6给出了对该运算放大器性能指标设计要求，模型中，EAv,EUGB,ESR和ETA分别表示增益、带宽、摆率和版图面积的期望值，λ为晶体管的沟道调制系数，CGDOP为PMOS的栅漏重叠电容，K′n和K′p分别为NMOS和PMOS的本征导电因子。PSRR+和PSRR-为正电源抑制比和低频负电源抑制比。

Table 6 Standard two-stage operational amplifier design characteristics requirements表6 标准两级运算放大器设计特性要求

分别设置EAv，EUGB，ESR，ETA，EPSSR+，EPSSR-，EPdiss，CL，L为50 dB，5 MHz，10 V/μs，400 μm2，60 dB，60 dB，2 mW，10 pF，2 μm,表7给出了4种算对标准两级运算放大器低频增益的优化结果，经过5 000次迭代,每种算法独立运行20次。由表7可知，PSO算法在5 000次迭代后找不到可行解，DGWO算法的均值结果明显优于其它3种算法,验证了DGWO在工程应用中的有效性。

Table 7 Standard two-stage operational amplifier low-frequency gain optimization results表7 标准两级运算放大器低频增益优化结果

6 结束语

本文对基本灰狼优化算法进行了改进，将反向学习和醉汉漫步融入其中，提出了DGWO算法。精英反向学习策略提高了种群多样性，扩大了搜索范围，醉汉漫步机制在提高灰狼优化算法收敛速度的同时，也提高了算法的收敛精度。本文在10个高维标准测试函数及CEC2013部分测试函数上对DGWO进行了仿真实验，结果表明,与PSO、GWO和GWO-CS 算法相比,DGWO算法在大部分函数上获得了较高的寻优精度，能有效处理高维函数及复杂函数优化问题，在单峰函数中具有良好的局部寻优效果，在多峰函数与组合函数中又体现出全局搜索能力得到加强。在开环低频增益优化问题中，与其它3种群体智能算法相比，DGWO算法在对比实验中具有优势，验证了该算法的有效性。