基于组合预测模型的小样本轴承故障分类诊断*
2021-09-23孙庞博陈安华蒋云霞
孙庞博,符 琦,陈安华,蒋云霞
(湖南科技大学计算机科学与工程学院,湖南 湘潭 411201)
1 引言
滚动轴承是机械设备中的核心部件之一,其运行状况关系到设备能否安全高效地运行,而设备长时间运行在恶劣的工作环境中,使轴承成为了旋转机械设备中最易损伤的部件之一[1]。故障诊断是提高机械使用可靠性,保障机械各部件长周期稳定运行,减少因故障停机带来经济损失的一种重要技术。传统的故障诊断方法借助专家领域知识从信号中人工提取特征,但由于信号的非线性、非稳态等特点,特征的提取与选择,以及诊断模型的建立与分析过程相当费时费力,因此,如何高效地提取有区分度的特征并对故障进行准确识别成为故障诊断领域的研究热点和难点[2]。
近年来,作为人工智能技术之一的深度学习方法发展迅速,由于其可以从海量数据中自主学习并提取特征数据,现已成功地应用于智能故障诊断等领域。深度学习方法常用的网络模型包括深度自编码器 DAE(Deep AutoEncoder)、卷积神经网络CNN(Convolutional Neural Network)、深度信念网络DBN(Deep Belief Network)和深度残差网络DRN(Deep Residual Network)等。这些网络模型通过对一维~三维输入数据进行原始时域信号预处理,提升模型的诊断效果。Sun 等[3]和Zhao等[4]分别通过小波包分析将原始振动信号转换为二维信号,并分别作为DRN模型和CNN模型的输入,提高了模型的效果;Shao等[5]提出一种改进的DBN模型,实现对故障特征的自动提取,克服了传统方法依赖手动设计特征的缺点。上述研究成果均在一定程度上提升了诊断模型的效果和故障分类的准确率,但也存在一些不足,如CNN模型需要对输入数据进行适应性改进或数据转换,DBN模型只能处理布尔量,无法直接处理实数域问题等,且大多数研究的实验效果都是基于故障样本充足的前提条件,在小样本故障数据条件下,上述方法将因无法学习到足够多的故障样本数据而导致效率低下。
因此,本文将以小样本故障数据为研究对象,基于变分自编码器VAE(Variational AutoEncoder)[6]原理,提出一种基于半监督VAE(SemiVAE)和LightGBM(Light Gradient Boosting Machine)分类模型的组合模型LSVAE(LightGBM-SemiVAE)。LSVAE可通过SemiVAE提取小样本数据的潜在特征,再利用LightGBM网络模型进行故障分类,并通过贝叶斯优化提升性能,从而克服传统VAE固有的生成的图像模糊、区分性较差等缺点,提升机械设备故障诊断效率。
2 变分自编码器


Figure 1 Structure of the variational autoencoder图1 变分自编码器结构

(1)
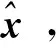

(2)



(3)
由于均值μ和标准差σ由神经网络计算,在随机采样的过程中无法求导,但是可以对采样的结果求导,因此可以通过反向传播优化网络性能。
虽然VAE通过引入变分下界使其在计算的过程中避免了复杂边界似然概率的计算,但也会带来新的问题,如生成数据趋于模糊,导致分类模型准确率下降等。
3 LightGBM预测模型
3.1 LightGBM原理
LightGBM[8]是一种分布式的梯度提升决策树增强框架,主要采用了直方图(Histogram)算法[9]和受深度限制的叶子生长(Leaf-wise)策略[10]相结合的思想,通过T棵弱回归树线性组合为强回归树,如式(4)所示,最终实现对大数据集或小批量数据样本的分类或回归。
(4)
其中,F(x)为最终的输出值,ft(x)为第t棵弱回归树的输出值。
在LightGBM中,(1)Histogram算法将连续型的特征值数据离散化为k个值,以生成宽为k的直方图,并将离散的训练数据值作为索引积累到直方图上,当遍历结束后,通过直方图的离散值来寻找决策树的最优分割点;(2)Leaf-wise策略在每次遍历所有叶节点时,找到分裂增益最大的叶节点(如图2中的黑色节点)继续分裂过程,并通过增加最大深度限制来控制决策树的访问深度和叶节点数量,从而避免过拟合现象和降低模型复杂度。

Figure 2 Growth process of Leaf-wise strategy图2 Leaf-wise策略生长过程
在进行数据并行的时候,LightGBM 可通过Histogram作差加速,一个叶节点的直方图可以通过其父节点与兄弟节点的直方图作差计算得到。利用该方法,LightGBM在构造叶节点时,可以通过少量的计算得到它兄弟叶节点的直方图,使计算量大幅度降低。
3.2 LightGBM超参数优化
LightGBM模型中有诸多需要手工调节的超参数,如最大树深度、执行分裂的最小信息增益、单位树的叶节点数等,这些参数的合理设置决定了模型预测结果的拟合速率和准确率等性能指标。传统的调参方法有随机搜索和网格搜索[11,12]等。其中,网格搜索是固定步长的穷举搜索法,对坐标空间中的每个点都进行计算,即可找到已知参数中的最优参数。但是,若网格步长不够小,网格搜索出来的最优参数可能与真实最优参数有较大距离;当步长足够小时,虽然可以找到全局最优参数,但是当坐标空间范围较大时,又可能导致大量无效的计算,使计算时间呈指数级上升。由于LightGBM模型参数众多,参数取值范围较大,若采用网格搜索参数,需要进行大量的计算,所以网格搜索不适用,而随机搜索又难以找到全局最优解,因此需要新的方法来解决LightGBM超参数优化问题。
具有主动优化特性的贝叶斯优化方法[13]对于复杂参数优化问题是一个有效的解决办法,该方法通过基于序列模型的优化来寻找全局最优解。贝叶斯优化本质上是使用概率代理模型来拟合真实函数,并根据拟合结果选择最优评估点进行下一步的评估,进而减少非必要的采样[14]。由贝叶斯定理可知(如式(5)所示),该方法利用已知信息对先验概率进行修正,进而计算出后验概率,同时可利用完整有效的历史评估结果来提高搜索效率。
(5)
其中,Y表示参数模型的参数;P(Y)表示先验概率模型;D为已观测向量集合;P(Y|D)表示目标函数的代理,由似然分布P(D|Y)修正得到。在每一次迭代后,更新概率代理模型,通过最大化采集函数,计算出新的评估点,并将其作为输入再次传入系统进行迭代,获取新的输出,以此更新已观测集合D和概率代理模型。
在参数模型中,常见的概率模型有高斯过程(Gaussian Processes)和树状结构Parzen估计方法TPE(Tree-structured Parzen Estimator)等,其中高斯过程具有高灵活性与可扩展性,在高斯过程中生成的多维高斯分布在理论上能够拟合任意线性/非线性函数,故本文提出的面向小样本数据学习的多分类算法中选择高斯过程对代理进行建模;采集函数则是采用了基于提升的策略EI(Expected Improvement),其具有参数少、可平衡深度与宽度之间的关系等优点。
在利用贝叶斯对LightGBM超参数优化的过程中,需要选择未知函数中的几个已知点作为先验事件,假设已选点服从多维高斯分布,根据高斯分布公式,可以计算出每一个点的均值与方差,即高斯过程由一个均值函数与一个半正定的协方差函数构成。假设x为输入数据集数据,在给定均值向量与协方差矩阵2个参数的条件下,参数Y将服从如式(6)所示的联合正态分布,以便对观测值yn与yn+1之间的关系进行递推计算。
(6)
若协方差矩阵(即核矩阵)记为K,因Y服从多正态分布,根据训练集可以计算得最优核矩阵,进而得出后验估计测试集Y*。根据高斯过程的相关性质,观测值集合y与预测函数值集合y*服从如式(7)所示的联合分布[15]:
(7)
其中,K*=[k(x*,x1),k(x*,x2),…,k(x*,xn)],K**=k(x*,x*)。
计算出联合分布后即可求预测数据y*的条件分布p(y*|y):
最后以均值作为预测数据的估计值,如式(8)所示:
(8)
4 组合预测模型LSVAE
组合预测模型LSVAE主要由半监督变分自编码器SemiVAE、多分类器LightGBM和贝叶斯超参数优化器3部分组成,如图3所示。
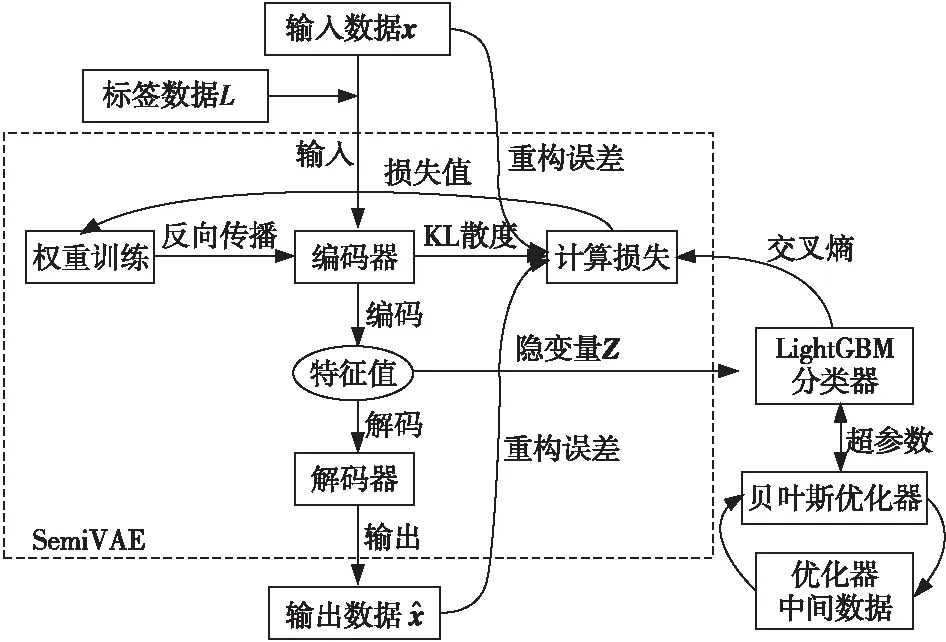
Figure 3 LSVAE model图3 LSVAE模型
图3中,SemiVAE利用标签数据对小样本空间数据进行半监督学习,以获得数据特征和隐变量Z;LightGBM基于隐变量Z的值进行多分类计算,并将结果反馈给SemiVAE计算损失,以便提高下一步训练的准确率;贝叶斯优化器则负责根据当前的计算结果对LightGBM的超参数进行自适应调整。
4.1 数据特征提取
本文模型使用半监督变分自编码器(SemiVAE)的编码过程得到均值向量μ和标准差向量σ,并通过重参数化技巧计算得隐变量Z,然后利用隐变量Z进行解码(Decoder)得到重建数据,其网络结构如图4所示。
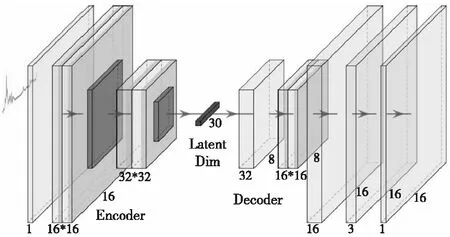
Figure 4 Network structure of LSVAE图4 LSVAE模型网络结构
4.1.1 编码(Encoder)过程
SemiVAE所用编码网络的输入长度为256的序列,通过折叠形成16*16的二维序列。网络包括4个卷积层、2个池化层和1个全连接层。每层卷积层后会有一个ReLU激活函数。卷积核为3*3,步长为1。经过卷积后并伸展会形成长度为1 024的特征向量。再经过编码网络后,会得到长度为20的特征向量,即为变分自编码器的均值向量与标准差向量,通过变换即可得到隐变量Z。
4.1.2 解码(Decoder)过程
解码网络对应编码网络,参数规格相同,即4个反卷积层、2个池化层,也采用ReLU激活函数,通过反卷积将低维特征映射成高维特征,再映射到低维度空间,最后输出长度为256(16*16)的序列。
4.2 损失函数构建
损失函数能够提升准确率,降低过拟合程度以及对抗欠拟合,所以损失函数的选择对计算结果有很大的影响。本文对损失函数的定义如式(9)所示。
Loss=κxeχxe+κklχkl+κreχre
(9)
其中,χxe表示交叉熵损失,χkl表示正则项损失,χre表示重建损失,超参数分别预设为κxe=2,κkl=1,κre=2。损失函数涉及到的交叉熵用于对抗模型趋近于模糊的懒惰性,提高准确率;KL散度为了增加泛化能力,显式建模隐变量分布。
4.2.1 交叉熵损失χxe
在半监督下,交叉熵用来衡量预测分布与真实分布之间的差异,在分类不明显的情况下可以对抗生成数据趋于模糊的缺点,使得输入数据对应的潜变量更具有区分性,具体计算公式如式(10)所示:
(10)
其中,xi表示输入数据集X的第i组,p(xi)表示真实分布,q(xi)表示预测分布。
4.2.2 正则项损失χkl
KL散度作用是比较2个概率分布的接近程度,SemiVAE与标准自编码器的区别在于对编码器添加约束,强迫它服从单位正态分布,进而限制隐变量Z空间的稀疏性,提高了泛化能力。相关计算公式如式(11)所示:
(11)
其中,σi表示标准差的第i个元素,μi表示L2正则项,J表示数据量。
4.2.3 重建损失χre
重建损失是指重建图像与真实图像的差异,通常表示为在多维空间中的欧几里得距离的平方,即均方误差,如式(12)所示:
(12)
其中,x′i为重建图像,xi为真实图像。
LSVAE模型所用算法伪代码如算法1所示。
算法1LSVAE伪代码



1.fori=1,2,…,epochsdo
2.SampleXtin minibatch;

4.Sampling:Zt←μZt+ε⊙σZ,ε~N(0,1);
5./*μZt是Zt的均值向量,σZt是Zt的标准差向量,Zt为第t次迭代的隐变量,ε采样于标准正态分布N(0,1)*/
6.Decoder:μXt←fθ(Zt);//μXt是Xt的均值向量
7.Compute cross entropy loss:
9.Compute relative entropy loss:
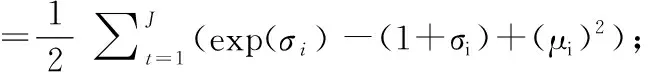
11.Compute reconstruction loss:
13.Fuse the three loss:
14.Loss=κxeχxe+κklχld+κreχre;
15.Back-propagate the gradients:
16.g←compute gradientθ,γ(θ,;Xt,ε);

18. //until maximum iteration reached
19.endfor
5 实验
5.1 故障数据集
5.1.1 数据源说明
本文使用的数据集来自凯斯西储大学CWRU(Case Western Reserve University)滚动轴承数据中心[16],该中心提供对轴承和轴承故障的测试数据,是世界上公认且流行的轴承故障诊断数据集。
CWRU滚动轴承数据的实验平台由一个1.5 KW的电动机(左)、一个扭矩传感器及编码器(中)、一个功率测试计(右)和电子控制器(未显示)组成,如图5所示。待检测的轴承支撑着电机的转轴,风扇端轴承型号为SKF6203,采样频率为12 KHz,驱动端的轴承型号为SKF6205,采样频率分别为12 KHz和48 KHz。

Figure 5 Rolling bearing fault data acquisition experimental bench图5 滚动轴承数据采集实验平台
CWRU轴承数据集中的滚动轴承有4种状态,分别是正常状态、内圈故障状态、外圈故障状态和滚动体故障状态。轴承的损伤来源于电火花加工时造成的单点损伤。SKF轴承用于检测3种直径为0.177 8 mm,0.355 6 mm,0.533 4 mm的损伤,NTN轴承用于检测直径为0.711 2 mm,1.016 mm的损伤。将特殊加工过的故障轴承装入实验平台中,分别在0 hp, 1 hp, 2 hp和3 hp(hp为马力)的电机负载下记录振动加速度信号数据,共获得8个正常样本、53个外圈损伤样本、23个内圈损伤样本和11个滚动体损伤样本。
5.1.2 数据集预处理
本实验将CWRU提供的轴承数据依据电机运行马力的不同分成3个数据集,每个数据集包含一个正常轴承数据、0.177 8 mm的3类故障数据和0.355 6 mm的3类故障数据,共7类数据,如表1所示。分别按照长度为128,256和512个数据点进行截取,并对其采用Min-Max线性归一化处理后,利用傅里叶变换为双边幅度谱数据,以便进行后续算法验证。
训练样本使用了数据集增强技术,一组实验数据共包含了电机负载分别在1 hp, 2 hp和3 hp状态下采集的3类数据,其中训练样本数为每一类数据40*s个(s∈{1,2,4,8}),测试集样本包含1 000个数据,且互不相交。
5.2 实验结果及分析
本文使用Python语言和TensorFlow开源框架[17]1.9版本搭建了模型开发与测试环境,模型数据流过程如图3所示。输入数据首先进入编码器,编码为潜变量,并进入分类器,然后解码,计算损失值,更新各参数,最后再输入测试数据测试模型效果。
为观察数据的数据量对结果的影响,按数据量和数据长度的不同,分别将本文与经典的KNN、CNN模型进行了测试对比,实验所用数据总量不超过7*80*512个样本。实验将测试10组数据分别改变每类数据量和单位数据长度进行测试对比,分组命名规则为:类别数*每类数量*单位数据长度l,对比分析的数据维度以l(l∈{128,256,512})进行替代计算,分别为7*40*l,7*80*l,7*l*128,7*l*256,如图6a~图6d所示,测试规格如表2所示,编码器参数预设值如表3所示。
从图6的对比分析可知,传统网络模型KNN
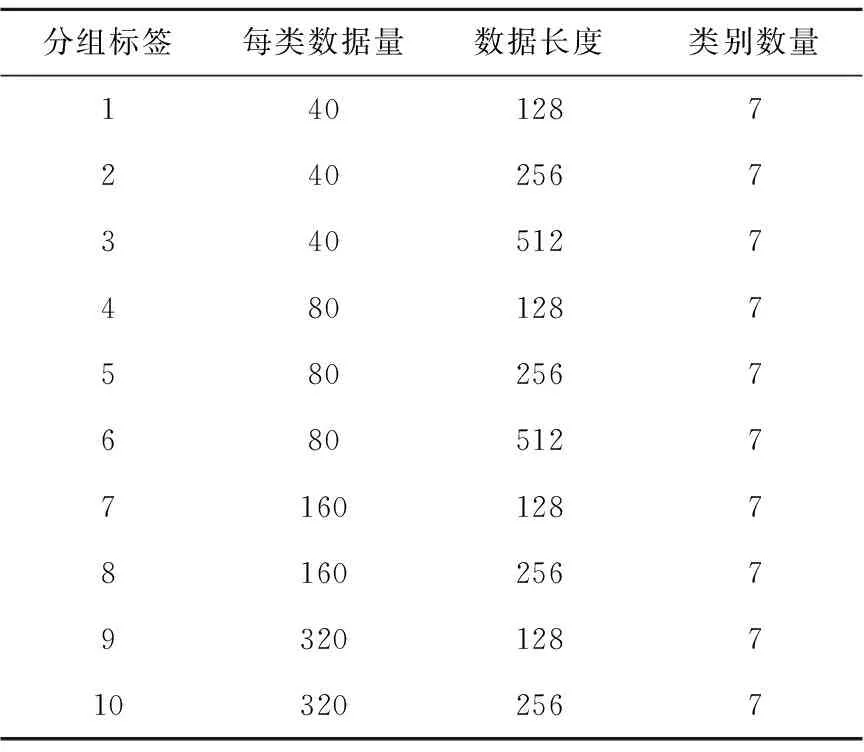
Table 2 Grouping format of data sets 表2 数据集分组规格
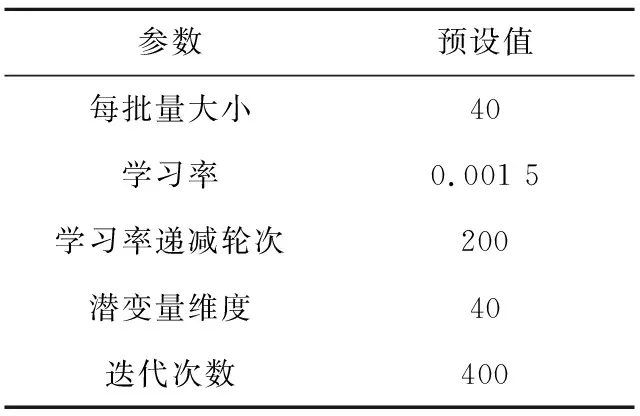
Table 3 Encoder parameter default values表3 编码器参数预设值
和CNN在小样本空间较小的情况下,对轴承故障分类诊断的准确率均低于LSVAE的,这主要是本文所使用的轴承数据是多组数据相关性较大的一维时序信号,而一般情况下CNN在二维数据上的表现会更好一些,如果将一维信号折叠,再将网络结构更改一下,确实可以提高准确率,但是模型相应地也会变复杂,进而导致需要的数据量增加,所以在小样本学习中CNN的表现难以达到预期;KNN可以在高维度空间中根据距离进行有效聚类分析,但是对于具有较大数据相关性的时间序列数据,难以利用距离直接进行特征提取和分析。本文提出的LSVAE通过SemiVAE迭代过程自适应进行特征提取与学习,同时在一定程度上避免了欠拟合的情况,再利用贝叶斯优化超参数改善过拟合的情况,从而在小样本数据学习中表现出了较优越的性能。
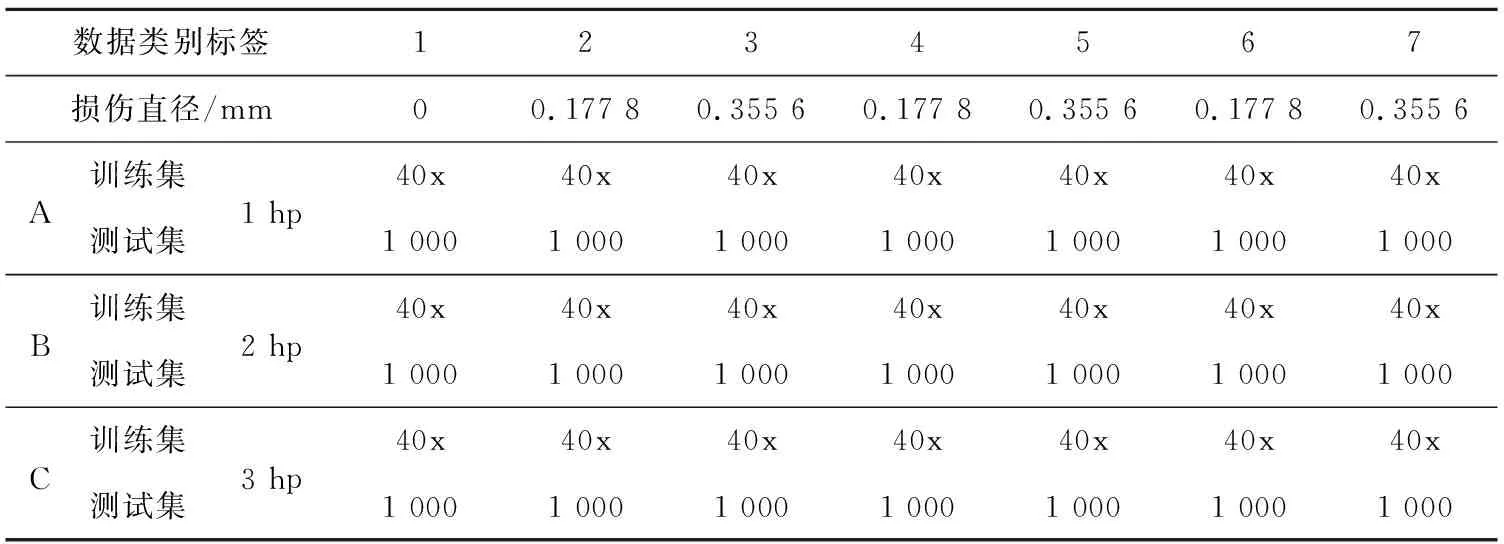
Table 1 Grouping description of Data Sets表1 数据集分组描述
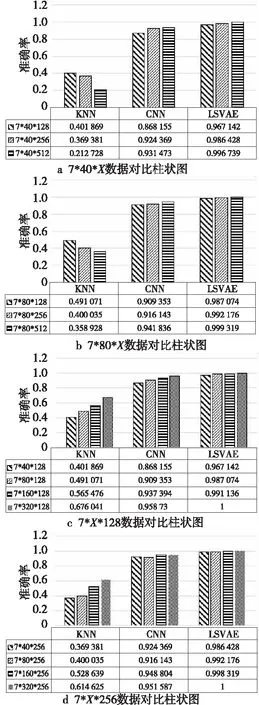
Figure 6 Comparison of different network models图6 不同网络模型对比
6 结束语
针对旋转机械设备中滚动轴承部件的故障数据分析与分类诊断问题,本文提出了一种结合变分自编码器与LightGMB分类模型的小样本学习模型LSVAE,并通过贝叶斯超参数优化增强性能,使得模型可以通过训练小批量的数据,得到良好的分类结果。实验结果表明:
(1)LSVAE模型可以从较小批量的时序信号中提取出有效的故障特征,且结果有着较高的准确率。
(2)相比于其他深度神经网络模型(CNN等),LSVAE在小批量数据测试中结果更稳定。
