基于时变需求的军事物流配送中心选址方法研究

2021-09-23陈庆印

国防交通工程与技术 2021年5期

田尧，陈庆印

(1.78092部队，四川成都 610031；2.军事科学院评估论证研究中心，北京 100091)

军事物流配送中心是构成军事物流网络的主干实体，在军事物流过程中起到关键的枢纽作用，选址合理的军事物流配送中心能够使军事物流过程更加高效，减少流通环节，降低配送成本，提高经济效益[1]。在综合需求动态特征、储备上限、运输限制、运转费用等各种限定条件的基础上，保证部队用户全方位、及时的物资保障，优化各类费用，以实现选址效益最大化，是军事物流配送中心选址问题的核心目标。同时，物流配送中心选址是一项战略决策，通常要考虑今后长时间的物资保障任务，因此在进行需求分析时应当充分研究物资的时变性、动态性特性。

目前，董鹏、卢苇等针对军事装备维修保障点选址问题，分别提出了基于BP和RBF神经网络的选址研究方法，构建了神经网络模型[2]。石红霞、王海兰采用重心法对战场油料物资配送中心进行初步选址，再用模糊层次分析法进行筛选[3]。李绍斌、杨西龙等以满足部队物资需求量为基本约束条件，以配送中心建设费用与配送成本之和为目标函数，建立多军事物流配送中心选址决策模型[4]。上述研究对于军事物流配送中心的选址优化具有一定现实意义，但所建立模型是传统的静态分析模型，不能有效应对物资需求量动态变化、时效要求、费用成本增长等情况，不利于战时保障。

本文针对上述研究不足，考虑战时保障实际情况，研究物资需求随时间动态变化的军事物流配送中心选址问题。

1 问题描述

军事物流配送中心选址，是在仓库和部队用户位置固定的情况下，已知仓库与备选点、备选点与部队用户的配送距离，配送中心的物资储备容量，中心开设成本、配送成本、储备成本等各类成本若干数量，配送工具的配送容量等多种条件下，从若干备选点中选择适当数量的选址点建设配送中心，以满足前方部队用户物资需求和后方仓库物资中转需求。

在军事物流体系运行时，军事物流配送中心处于物资配送链的中游，其上游主要是各类专业仓库和综合仓库，下游是有时变物资需求的部队用户，如图1所示。配送中心在体系中主要起到承上启下的作用，即从后方仓库接收军用物资，并进行军用物资的存储、分炼，按时间向前方部队用户配发运输军用物资。

图1 时变需求下的军事物流基地体系运行过程

部队用户的物资需求随时间发生变化，具有时变性；仓库到配送中心、配送中心到部队用户的物资配送受到时间约束，具有时效性；仓库、配送中心的物资储备量随时间动态变化，具有动态性。为了有效描述上述时变性、时效性、动态性等特征，需要加入时间变量，对军事物流配送体系运行的全过程进行数学建模，对时变需求下军事物流配送中心的选址进行分析研究。

2 模型建立

2.1 模型假设

为了方便模型建立，需要对配送中心选址问题进行基本假设：①仓库与配送中心、配送中心与部队用户构成配送关系，仓库不直接向部队用户配送物资；②仓库与配送中心备选点、配送中心备选点与部队用户的配送距离已知，且物资单位配送距离费用已知；③部队用户的物资需求已知，且随时间动态变化；④各备选点的配送中心开设费用不同，反映出不同地点选址成本差异性。

2.2 模型参数

I为仓库集合，用i遍历；J为配送中心备选点集合，用j遍历；δi为初始时间仓库i的物资储备量；K为部队用户集合，用k遍历；ωj为备选点j的物资初始物资储备量；T为时间集合，用t、t′遍历；φj为备选点j的物资最高储备量；Oj为是否在备选点j选址，1为是，0为否；αj为单位时间备选点j的物资最大接收量；Ri,j,t为时间t仓库i给备选点j的物资配送量；βk为单位时间部队用户k的物资最大接收量；Cj,k,t为时间t备选点j给部队用户k的物资配送量；γ为单位时间下单位物资的配送成本；Sj,t为时间t备选点j的物资储备量；μj为备选点j的配送中心建设成本；Xi,t为时间t仓库i的物资储备量；χi为单位时间仓库i的单位物资储备成本；ψj为单位时间备选点j的单位物资储备成本；n为配送中心开设数量；ρi,j为仓库i到备选点j的物资配送时间；πk,t为时间t部队用户k的物资需求量；θj,k为备选点j到部队用户k的物资配送时间。

2.3 模型构建

根据上述模型假设和参数设定，构建军事物流配送中心选址模型：

(1)

(2)

(3)

(4)

Xi,t=δi∀i∈I,t∈T∩t=1

(5)

(6)

Sj,t=ωjOj∀j∈J,t∈T∩t=1

(7)

(8)

Sj,t≤φjOj∀j∈J,t∈T∩t≥2

(9)

(10)

(11)

(12)

Ri,j,t≥0Cj,k,t≥0Sj,t≥0

Oj∈{0,1} ∀i∈I,j∈J,t∈T

(13)

目标函数(1)表示配送中心选址的目标约束是最小化各项成本费用，即选址建设成本、物资配送成本和物资储备成本之和；约束函数(2)对备选点选址数量进行约束；约束函数(3)表示某个仓库到各备选点物资累积配送量不能超过该仓库自身物资初始储备量；约束函数(4)表示所有仓库配送到某个备选点的物资配送量不能超过该备选点自身的物资最大接收量，若不选择该备选点则物资配送量直接为0；约束函数(5)表示对仓库的初始物资储备量做出限定；约束函数(6)表示仓库的物资储备量等于上一时间的物资储备量与本时间物资配送量之差；约束函数(7)考虑到在开始时间物资并未送到物资配送中心，因此该时间物资储备量是自带物资量；约束函数(8)表示备选点的物资储备量等于上一时间的物资储备量与本时间到达该备选点的物资配送量之和，再减去从该备选点出发的物资配送量；约束函数(9)表示某个备选点的物资储备量不能超过自身最大储备量，若不选择该备选点则物资储备量为0；约束函数(10)表示某个备选点向外的物资配送量不能超过该时间自身的物资储备量；约束函数(11)表示所有备选点向某个部队用户的物资配送量，不能超过该部队用户的物资最大接收量；约束函数(12)是对物流配送中心完成配送任务的限定，表示截至时间t所有备选点向某个部队用户的累积物资配送量，要超过该部队用户在时间t的物资需求量；约束函数(13)是对各变量的取值范围限定。

3 应用算例

3.1 算例描述

某联勤保障部队拟在8个备选点中选出4个作为配送中心的选址地点，在10个时间阶段可以储备周转来自后方6个仓库的军用物资，并同时满足前方5个部队用户的动态物资需求。问如何对配送中心进行选址，以在满足部队用户在多个时间阶段物资需求的前提下产生的经济效益最高。

各参数设定如下：部队用户的物资需求在区间[20,60]中随机产生；初始时间仓库的物资储备量服从正态分布N(350,302)；备选点初始时间物资储备量服从正态分布N(60,152);备选点的物资最高储备量服从正态分布N(85,102)；单位时间备选点的物资最大接收量服从正态分布N(70,82)；单位时间部队用户的物资最大接收量服从正态分布N(60,52)；配送中心建设成本在区间[500,800]中随机产生；单位时间仓库的单位物资储备成本在区间[40,60]中随机产生；单位时间备选点的单位物资储备成本在区间[60,100]中随机产生；仓库到备选点的配送时间在区间[0.1,0.5]中随机产生；仓库到备选点的配送时间在区间[0.5,1]中随机产生。

3.2 计算结果

对上述构建的数学模型使用Lingo17进行程序编写，部分核心代码为：

min = @sum(J(jj):mu(jj)*O(jj))+gamma*@sum(I(ii):@sum(J(jj):@sum(T(tt):rho(ii,jj)*R(ii,jj,tt))))+gamma*@sum(J(jj):@sum(K(kk):@sum(T(tt):theta(jj,kk)*C(jj,kk,tt))))+@sum(I(ii):@sum(T(tt):chi(ii)*X(ii,tt)))+@sum(J(jj):@sum(T(tt):puxi(jj)*S(jj,tt)));

@sum(J(jj):O(jj))=n;

@for(I(ii):@sum(J(jj):@sum(T(tt):R(ii,jj,tt)))<=delta(ii));

@for(J(jj):@for(T(tt)|tt#gt#1:@sum(I(ii):R(ii,jj,@floor(tt-rho(ii,jj))))<=alpha(jj)*O(jj)));

@for(I(ii):X(ii,1)=delta(ii));

@for(I(ii):@for(T(tt)|tt#gt#1:X(ii,tt)=X(ii,tt-1)-@sum(J(jj):R(ii,jj,tt))));

@for(J(jj):S(jj,1)=omega(jj)*O(jj));

@for(J(jj):@for(T(tt)|tt#gt#1:S(jj,tt)=S(jj,tt-1)+@sum(I(ii):R(ii,jj,@floor(tt-rho(ii,jj))))-@sum(K(kk):C(jj,kk,tt))));

@for(J(jj):@for(T(tt):S(jj,tt)<=phi(jj)*O(jj)));

@for(J(jj):@for(T(tt):@sum(K(kk):C(jj,kk,tt))<=S(jj,tt)*O(jj)));

@for(K(kk):@for(T(tt)|tt#gt#1:@sum(J(jj):C(jj,kk,@floor(tt-rho(jj,kk))))<=beta(kk)));

@for(K(kk):@for(T(tt):@sum(J(jj):@sum(T(tt_)|(tt_#le#tt)#and#(tt_#gt#1):C(jj,kk,@floor(tt_-rho(jj,kk)))))>=@sum(T(tt_)|(tt_#le#tt)#and#(tt_#gt#1):pi(kk,tt_))));

@for(I:@for(J:@for(T:@gin(R))));@for(J:@for(K:@for(T:@gin(C))));@for(J:@for(T:@gin(S)));@for(J:@bin(O));

代入预设模型参数，对程序运行，Lingo17求解器状态(Solver Status)如图2所示，所构建的模型属于混合整数二次规划模型(MIQP)，变量共计1 042个，约束469个，非零系数6 380个。该程序由于参数量较大，导致运行时间较长(Elapsed Runtime)，迭代次数较多，经过1 h 13 min 7 s的14 190 273次迭代，程序运行完毕，求得全局最优解(Global Opt)，目标函数值为636 378。

图2 Lingo17求解器状态

计算求得的选址方案是选择备选点1、2、6、8作为配送中心的建设地点。这几个备选点的建设成本较低，自身物资储备能力和接收能力较强，与仓库、部队用户的配送时间较短，能够在规定时间内满足部队用户的物资需求。

仓库随时间变化的物资储备量如图3所示。随着时间变化各仓库内的储备物资逐渐减少，这是仓库为了满足前方部队用户物资需求，向备选点不断配送物资的结果。物资储备量按照仓库1、仓库5、仓库6、仓库3、仓库2、仓库4的顺序逐个耗尽，说明各个仓库所担负的物资配送任务具有时间阶段性。

图3 仓库的物资储备时变量

仓库随时间变化的物资配送量如图4所示。从图中可以看出，在不同时间阶段仓库的分工不同，时间2、时间3主要是仓库1、仓库5和仓库6担负物资配送任务，时间4、时间5主要是仓库3、仓库5和仓库6，时间6、时间7主要是仓库2、仓库3和仓库4，时间8和时间9主要是仓库4。时间1和时间10属于配送任务的开始和结束时间，开始时间备选点没有物资需求，结束时间部队物资需求已经被满足，因此没有配送任务。这种良好的配送任务分工秩序能够明确各仓库间的责任分工，有效提高物资配送效率。

图4 仓库的物资配送时变量

备选点随时间变化的物资储备量如图5所示，各备选点的物资储备量较为稳定，能够为部队用户提供持续稳定的物资保障。备选点储备量除了在时间2和时间10，其余时间较为稳定，这是因为备选点在向外配送物资的同时，也会接受来自仓库的物资，使得自身的物资储备量处于一种动态平衡之中。在时间2，前方部队用户产生了物资需求，备选点向外配送了大量物资，而此时从后方仓库补充的物资暂时还未完全到位；在时间10部队用户产生的物资需求一定要在整个任务时限内(时间10)完成，若此时备选点配送物资则会超出任务时限，因此备选点选择在时间9～10之间提前配送物资。

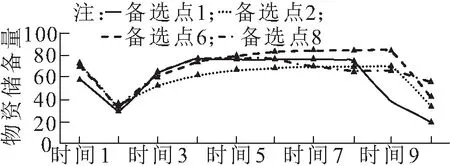
图5 备选点的物资储备时变量

备选点随时间变化的物资配送量如图6所示。可以看出，在不同时间各个备选点的物资配送量较为平均、差异性不大，说明备选点的配送物资任务分配较为公平。在时间点2，各备选点的向外物资配送量较少，主要是为了即时满足部队用户在时间1产生的物资需求，备选点在时间1向外配送了大量物资，此时备选点的物资补充仍没有到位，体现出备选点保障部队用户的反应灵敏性较强。