基于模糊聚类法探究扰动对同调分群的影响
2021-09-23林谷烨黄振琳杨宸瑄
林谷烨, 黄振琳, 杨宸瑄
(1.华南理工大学 电力学院,广东 广州 510641;2.广东电网有限责任公司 电力科学研究院,广东 广州 510062)
0 引 言
电力系统中同调机群的识别在电力系统动态特性研究中有着广泛的应用[1]1。正确识别同调机群对于研究电力系统稳定性具有重要意义。同调识别的方法大体上可以分为基于模型参数的方法和基于发电机功角曲线的数据挖掘法[2]。
目前研究发现同调机群划分准则具有一定的模糊性和不确定性,根据这一特性将模糊聚类引入同调机群的识别具有一定优势[3]。文献[1]2将自组织神经网络与模糊聚类相结合来进行发电机同调机群的识别,需要读取发电机故障时持续的功角变化以及切除时刻的动能作为特征输入进行样本训练。文献[4]用系统机电距离作为聚类的量化指标。以上方法应用模糊聚类进行同调机群的识别已经取得较好的效果,但并没有探究扰动会对分群方式有什么影响。
为了改进同调分群方式,本文先用文献[5]的建模方法形成同调模糊集,再应用模糊聚类法进行同调分群。接着从发电机模型上分析扰动对分群结果影响,并在IEEE 39节点上进行试验,验证该结论。
1 发电机同调聚类模型的建立
1.1 模糊聚类原理介绍
聚类分析是按照某种标准对事物进行分类的数学方法。即:
设有n个事物的总体(论域X):
X={x1,x2,x3,x4,…,xj,…,xn}
(1)
式中:xj为第j个事物的特征。
每个事物抽取s个特征:
xj={xj1,…,xjk,…,xjs},(j=1,…,n)
(2)
式中:xjk为第j个事物的第k个特征的观测值。聚类问题就是按某种标准来鉴别事物之间的接近程度,并把彼此接近的事物归为一类[6]87。
本文采用传递闭包法进行同调分群,该方法聚类过程简便且分类数呈动态性。
1.2 模糊聚类分析步骤
1) 建立模糊相似矩阵[7-8]
模糊相似矩阵的构建是按某种方式给论域X中的元素两两之间赋予[0,1]内的一个数,称之为相似系数r,以此表示这两个元素的相似程度,来构建模糊相似矩阵R。
选择算术平均法作为模糊相似矩阵的标定方法:
(3)
式中:s为每个事物有s个特征;min为求两个元素值中较小值的函数;Xim为第i个事物的第m个特征的观测值;rij为i、j之间的相似系数。
两两元素经过标定之后即可得到模糊相似矩阵R:
R=[rij]n×n
(4)
式中:rij为模糊相似矩阵R中第i行第j列的元素,也表示i,j之间的相似系数。
2) 构建模糊等价矩阵
经过标定以后,矩阵R满足自反性及传递性,是模糊相似矩阵。满足传递性,即可成为模糊等价矩阵。
若要满足传递性,这里可采用矩阵自乘的方法,对R进行n次自乘直至出现Rn=Rn+1,则此时的R*=Rn即为所求的模糊等价矩阵,其中该自乘不同于矩阵的平方法,而是用最大最小求得,即:
(5)
式中:ri1~rnj为模糊相似矩阵R中相应的元素;min(ril,r1j)为取其中两个元素数值的最小值,max表示取最大值。
3) 动态聚类
动态聚类是确定一个判断是否分为一类的标准数λ,即给定一个数λ,若rij≥λ,则说第i个元素与第j个元素是归为一类,同调的。
1.3 建立基于模糊聚类的发电机同调模型
在电力系统的暂态稳定的动态过程中,总有一些机组的动态行为是相似的,这些机组称为同调机群[9]。若两台机的相对转子角偏差在任意一个t∈[0,τ]时刻内都比给定的标准ε(>0)小,则判定这两台机关于τ时间区段内同调。即:
(6)
式中:max为取元素最大值;δi(t)为发电机i在t时刻的功角,通常可取ε=5°~10°,τ=1~3 s。根据式(6),则可将全部发电机进行同调分群。
因此发电机间转子角的偏差是判别发电机是否同调的依据。列出发电机转子运动方程,从中提取判断发电机同调的特征值建立模糊相似矩阵。
(7)
式中:δ为转子位置角;ω为电气角速度;ωN为发电机额定角速度;Pm为机械功率;PD为阻尼功率;Pe为电磁功率;TJ为机组转子惯性时间常数。
电磁功率表达式为:
(8)
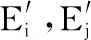
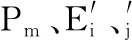
文献[11]的化简方法可得分析发电机同调的关键方程:
(9)
式中:Ti为发电机i的惯性时间常数;ωi为发电机i的电气角速度;δi、δj为发电机i、j的转子位置角。
从中得:
(10)
式中:kij为发电机i、j之间的同调特征系数。
作为模糊聚类中判定发电机同调性的标准,形成同调识别的模糊集矩阵如式(11)所示。
(11)
式中:kij为组成的发电机同调特征系数集合成的同调模糊集矩阵K的元素。
这个矩阵K能体现出发电机的初始功角,发电机间的网络连线等因素,可以映射出发电机动态过程中发电机的同调程度[6]88。
综上所述,可得基于模糊聚类的求解发电机同调机组的流程如图1所示。
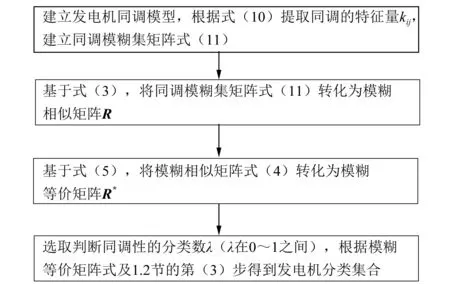
图1 建立发电机同调聚类模型流程图
2 基于高斯消去法的扰动探讨分析
由式(11)可得影响发电机同调性的因素有发电机暂态电压、内电势节点导纳以及发电机间功角差,其中只有发电机内电势节点导纳矩阵在发生故障的时候是会突变的。
因此仅考虑故障对发电机内电势导纳矩阵存在的影响。
为了分析大扰动对发电机等效导纳矩阵的影响,本文按“发电机节点→故障节点(设大扰动发生在端点分别为m,n的线路上)→其余节点”的顺序列写节点导纳矩阵Y,如式(12)所示。再利用高斯消去法将导纳矩阵Y简化至仅剩发电机节点和线路故障两端节点的矩阵Y(本文称为过渡导纳矩阵)。最后再用高斯消去法消去过渡矩阵中的大扰动线路端点,得到等效导纳矩阵Y#。
高斯消去法将节点从外向里消去,即从式(12)的矩阵Y中最外面的第k个节点开始消去,当消除节点j时,删去矩阵Y第j行第j列,且矩阵Y里的剩下的第a行b列矩阵因子yab变为:
(12)
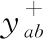
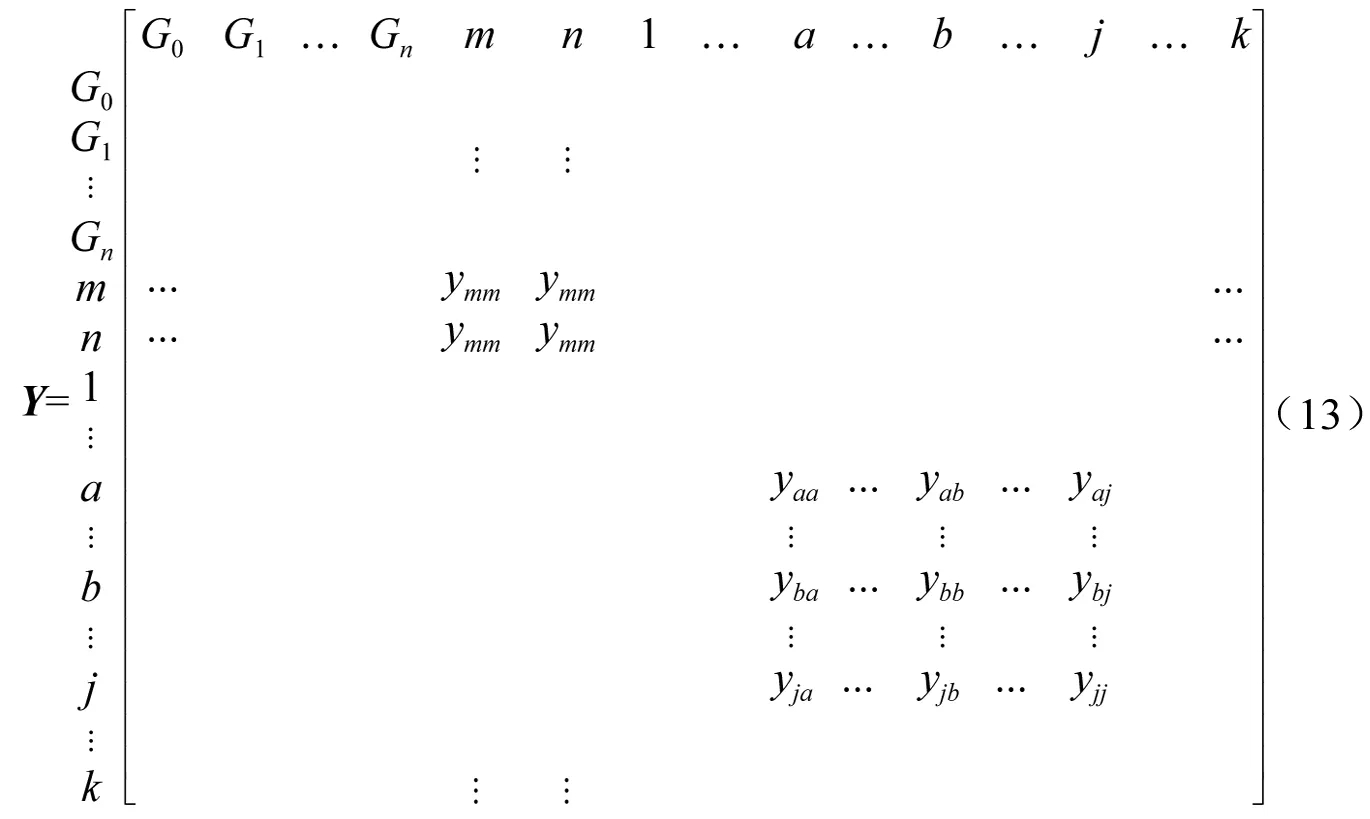
接下来对比大扰动前后导纳矩阵Y和Y*相应的过渡矩阵Y′和(Y*)′的差异。由式(12)可知,故障前后Y和Y*仅故障线路两端节点的自导纳ynn、ymm和互导纳ynm、ymn不同。因此经过式(12)变化后,Y′和(Y*)′仍仅故障线路两端节点不同。即
(14)
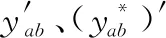
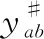
(15)
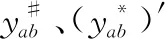
推论1:对于与故障节点电气距离较近的发电机,故障前后该发电机与其他发电机间的等效导纳变化也较大。
综合式(10)以及推论1可得推论2。
推论2:离故障节点电气距离较近的发电机,更有可能与原同调机群失去同调性。
3 IEEE 39节点算例验证
本文在如图2所示的IEEE 39节点系统中进行仿真验证。由于平衡机的功角一直为0,讨论其同调性意义不大,后续试验忽略平衡机节点G9。
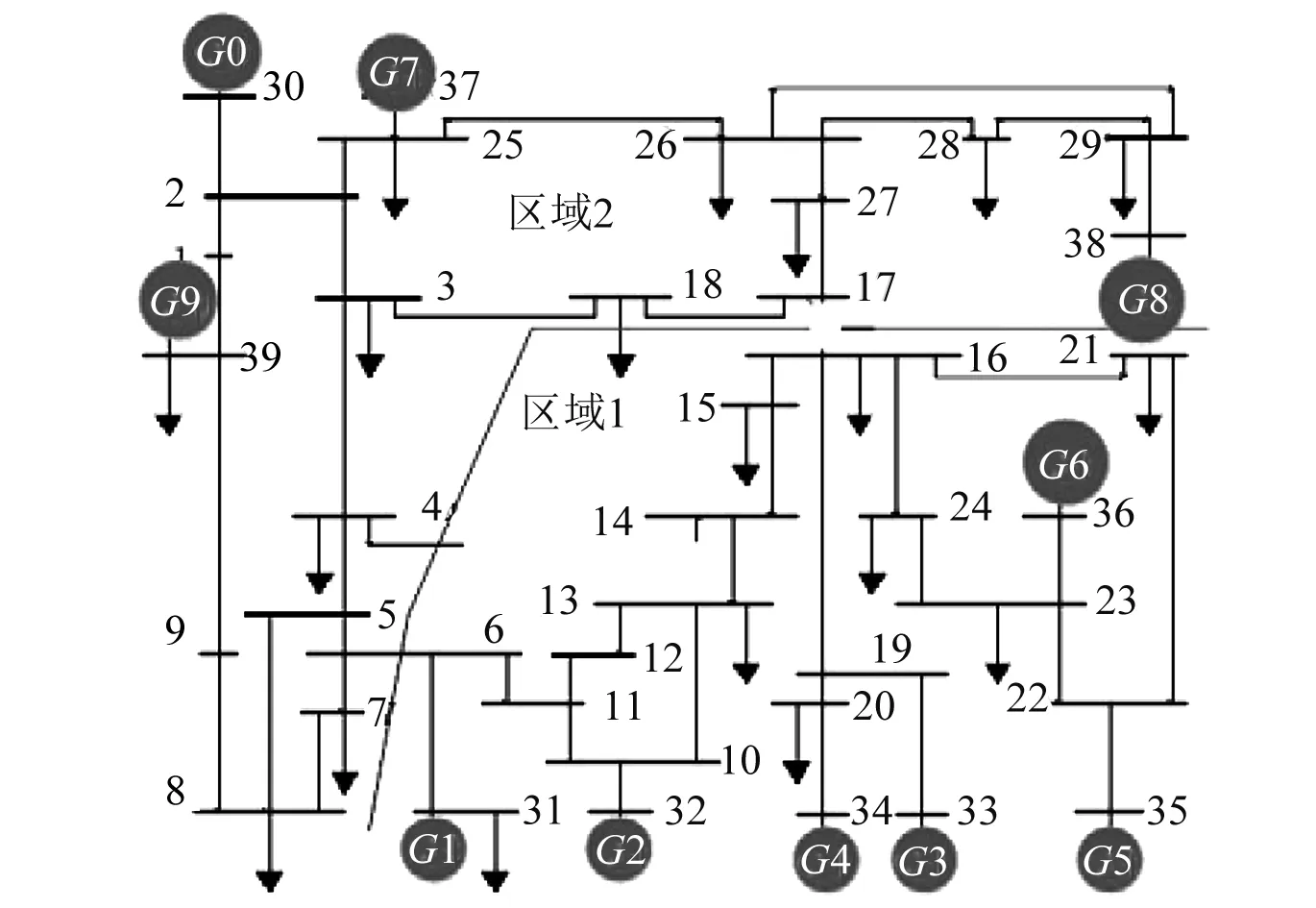
图2 IEEE 39节点系统
先计算原始模糊等价矩阵:
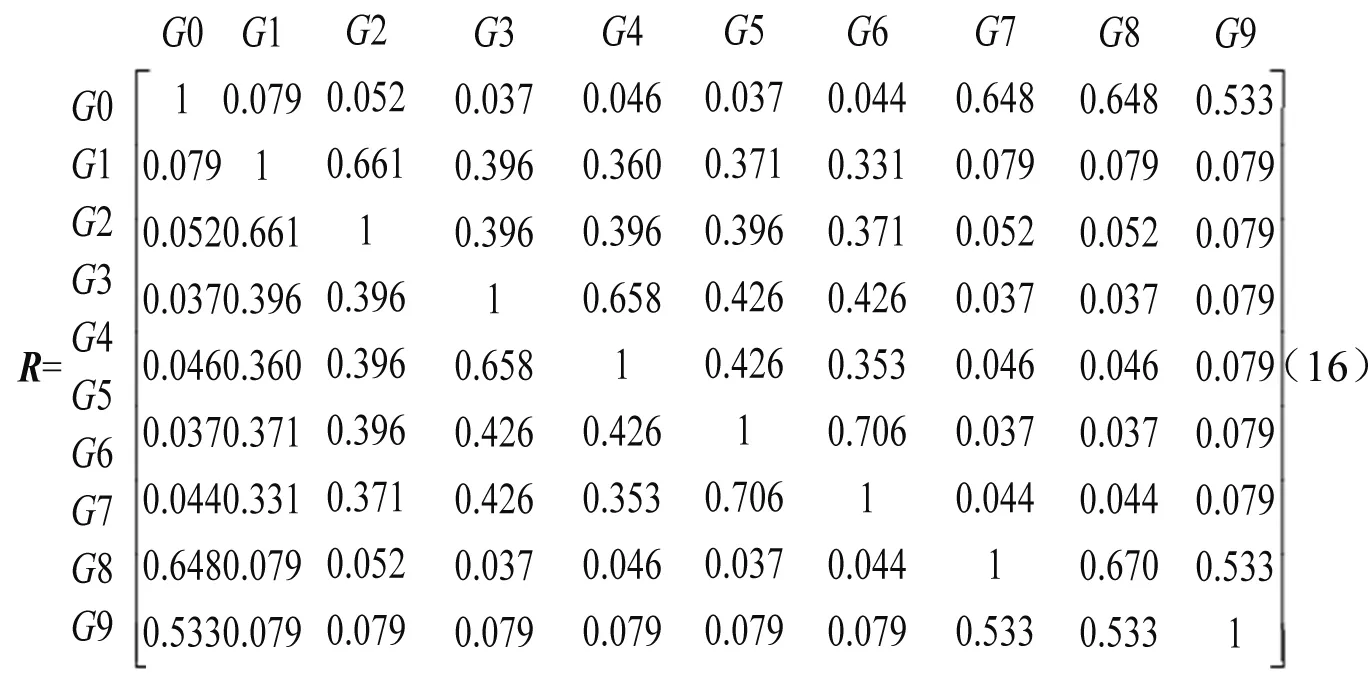
取动态聚类数λ=0.3可得分群结果:
第一组:G0,G7,G8
第二组:G1,G2,G3,G4,G5,G6
通过对母线12采取减去100 MW的有功负荷这种小扰动来验证初始分群正确性,并利用BPA以及MATLAB得到发电机功角仿真图,如图3所示。为了清晰看出各发电机功角曲线的差别,将每个发电机的功角曲线起始点均平移至0点,且用“功角变化量”作为纵坐标。
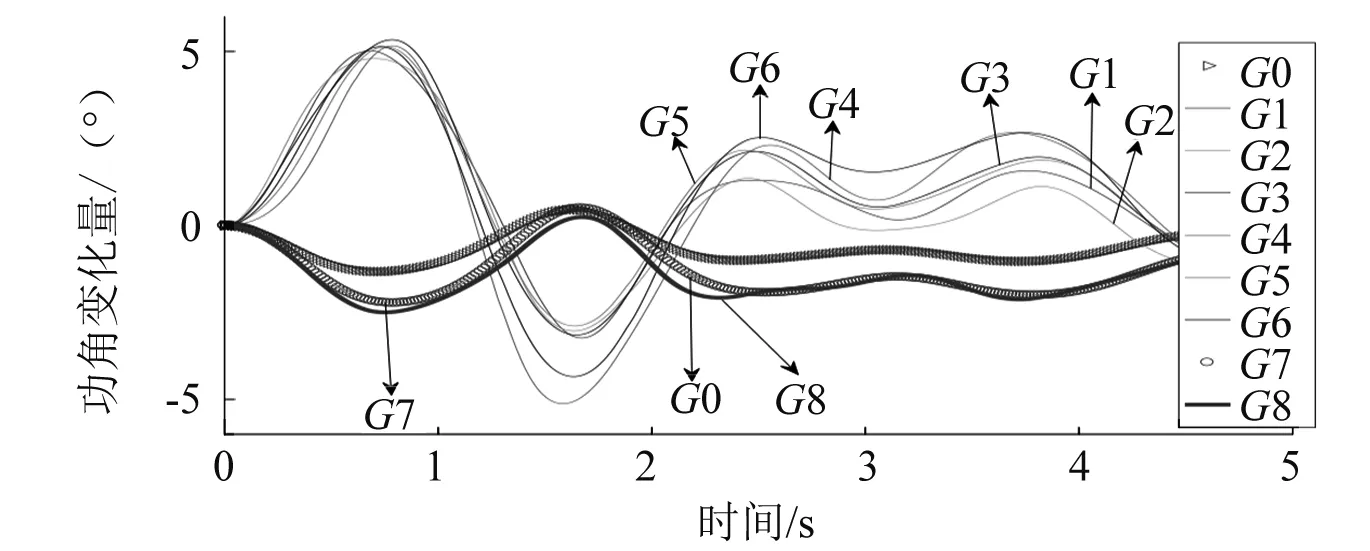
图3 初始分群结果下的功角仿真图
为了能验证第二节推论的正确性。随机选取了三条线路,分别作为故障来提取数据制图。按离故障的远近(依据各个发电机离故障线路的等效阻抗/导纳的大小)来依次排列发电机(由近到远排列),在线路故障前后的发电机内电势电纳以及聚类矩阵相减得到的变化矩阵用MATLAB制作三维视图,以发电机号为X、Y轴,故障前后电纳/聚类矩阵相减得到的变化矩阵为Z轴,绘制图形,如图4~图6所示。
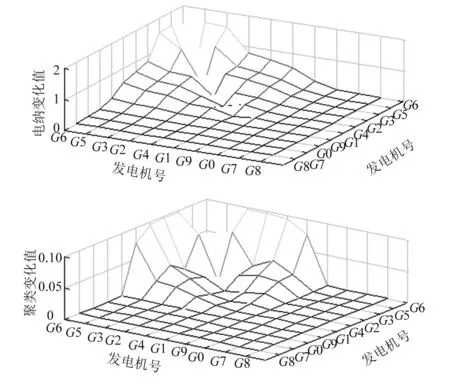
图4 线路23~24电抗与聚类矩阵变化图
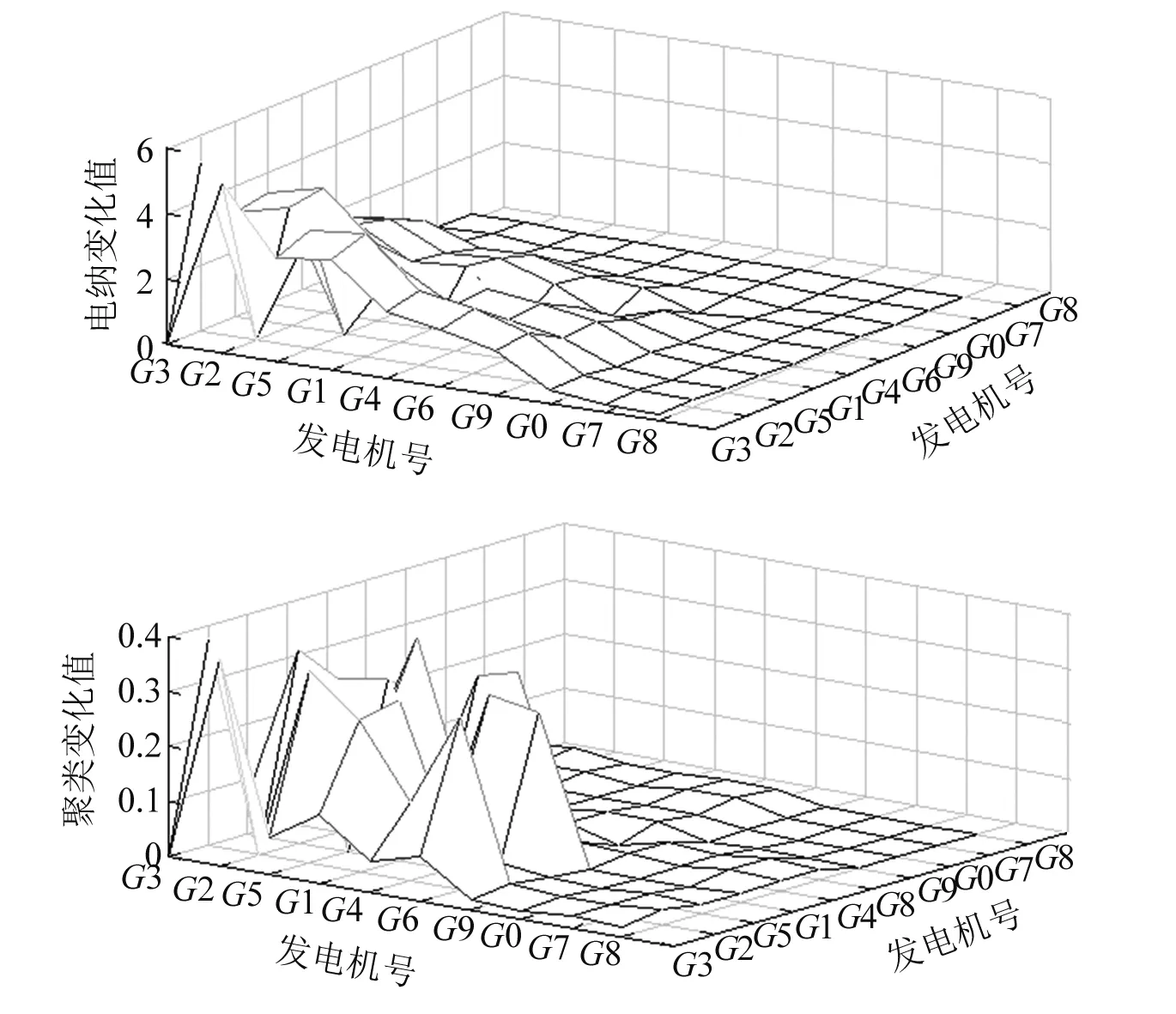
图5 线路14~15电抗与聚类矩阵变化图
从图4~图6能看出,离故障点较近的发电机才有较大变化,聚类结果变化的趋势与导纳结果变化的趋势接近。因此可以得到故障会影响发电机间互电纳数值来影响聚类的结果。
以线路23-24故障为例用BPA以及MATLAB软件作出此时的功角仿真图如图7所示。线路23~24在 0.4 s开始短路故障,0.5 s线路被切除。
将图7与图3进行比较可得:G5、G6发电机与其原同调机群其他发电机功角曲线出现了较大的不同。而图3也能看出这两台发电机离故障点较近,验证了上面所述的离故障点较近的发电机影响较大的结论。
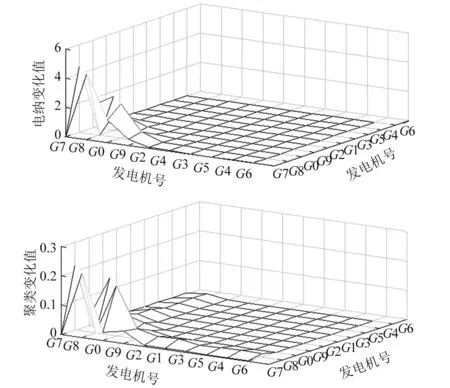
图6 线路25~26电抗与聚类矩阵变化图
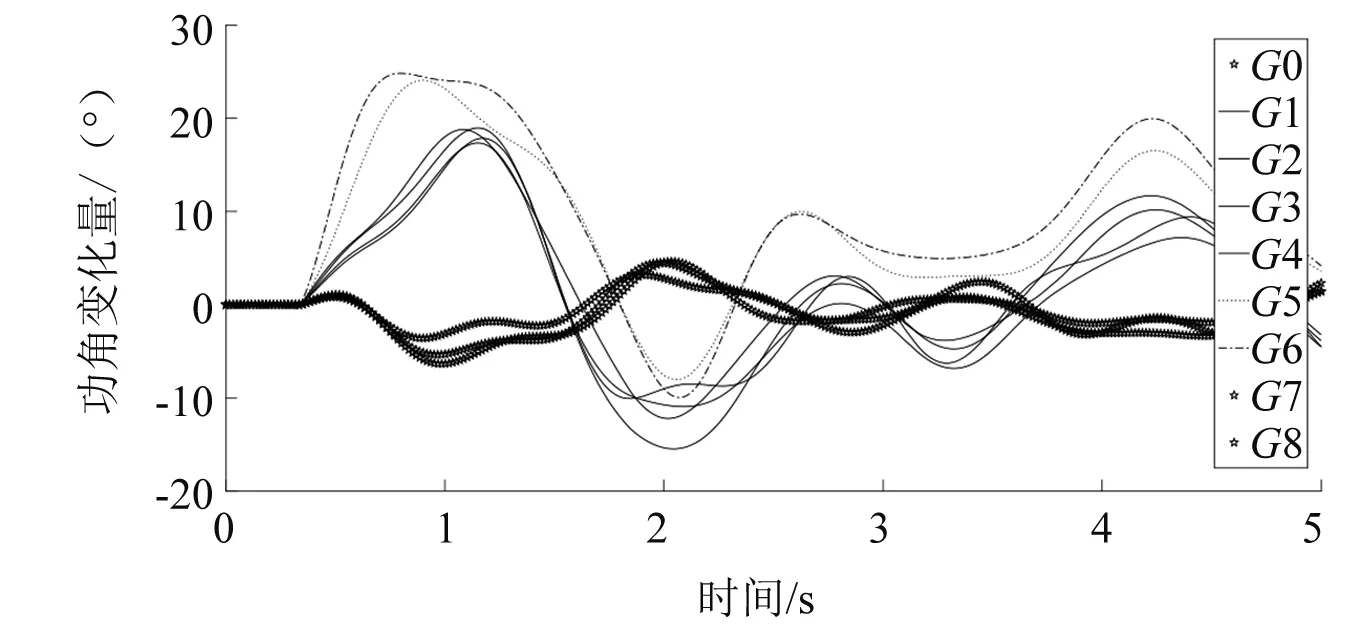
图7 线路23-24故障后系统功角仿真图
4 结束语
本文从聚类模型出发,分析影响同调性的故障因素;然后通过高斯消去法分析扰动会对导纳矩阵产生影响,以及对最后结果造成的影响;最后用39节点系统来验证结论。
通过本文的分析论证,可以得到以下几个结论:
(1) 离故障点近的发电机与其他发电机之间的互导纳值在故障前后会产生较大的变化。
(2) 两台发电机间聚类值的变化与两台发电机间互电纳值的变化成正相关关系。
(3) 相较于基于故障前稳态信息的同调机组分群结果,不同故障情况可能会对其产生局部影响,且只有离故障点比较近的发电机才有可能与原同调群失去同调性。
接下来将在本文研究基础上继续研究如何实现发电机在故障后的快速分群。可以辅助研究人员在电力系统故障后进行快速同调动态等值分析,更快对故障进行相应的处理。从某种意义上来说,可以提高电力系统的稳定性。
