基于自适应卡尔曼滤波的负荷参数在线辨识方法

李红霞，李尚远，李振垚，甘德强

(浙江大学 电气工程学院，浙江 杭州 310027)

0 引 言

随着我国电力系统的发展，电力系统规划调度和故障分析主要依赖于软件建模和分析，负荷模型参数的准确性对电力系统的安全稳定运行有重要意义[1]。传统负荷建模方法主要有统计综合法、故障拟合法和总体测辨法[2-3]。总体测辨法根据经验选择负荷模型，运用大扰动数据寻找最优参数，使得输入输出关系接近实际测量值，但负荷时变性，大扰动时刻辨识的负荷模型无法代表实际负荷。近年来随着广域测量系统(wide area measurement system, WAMS)的发展，其测量单元(PMU)提供了实时测量的小扰动运行数据。相对于来自系统响应信号或者人工激励信号的大扰动数据，负荷模型在小扰动环境下可以当作一种线性系统，方便进行模型选择和计算。

由于小扰动数据类型较少、信噪比较低，在具体辨识过程中应考虑减少噪声的影响。1960年美国科学家卡尔曼在系统状态空间模型基础上提出了卡尔曼滤波，在线性滤波问题上得到了考虑噪声影响的解析解[4-6]。但传统卡尔曼滤波器常因不能满足理想条件，而造成实际滤波效果不佳，甚至滤波发散[7]。因此，学者们提出了多种改进算法。Rouhani等人[8]提出了一种基于非线性观测器寻找负荷参数最优解的扩展卡尔曼滤波算法。Wang等人[9]提出了一种在线性离散系统中过程噪声完全未知时估算过程噪声协方差矩阵的算法。然而现有研究中，结合PMU实时数据，运用自适应卡尔曼滤波辨识线性负荷模型参数的研究较少。

针对以上问题，本文提出一种迭代测量噪声的改进Sage-Husa自适应卡尔曼滤波方法。应用预报误差法的思想，分别用卡尔曼滤波和自适应卡尔曼滤波对负荷模型的参数进行对比辨识，浙江电网华金变电站PMU数据的算例验证了本文算法在负荷模型辨识中的有效性。

1 待辨识综合负荷模型

本文采用的负荷模型为PSASP程序的综合负荷模型，运用文献[10]的综合负荷模型线性化方法，得到本文连续状态空间模型如式(1)所示。

(1)

式中：u为输入变量，u=[ΔVΔθ];y为输出变量,y=[ΔPΔQ];x为状态变量，x=[ΔExΔEyΔs];e(t)为过程噪声;v(t)为测量噪声;Gc和Hc为过程噪声的系数矩阵;Ac、Bc、Cc和Dc分别为变量的系数矩阵，具体如式(2)～式(5)所示。

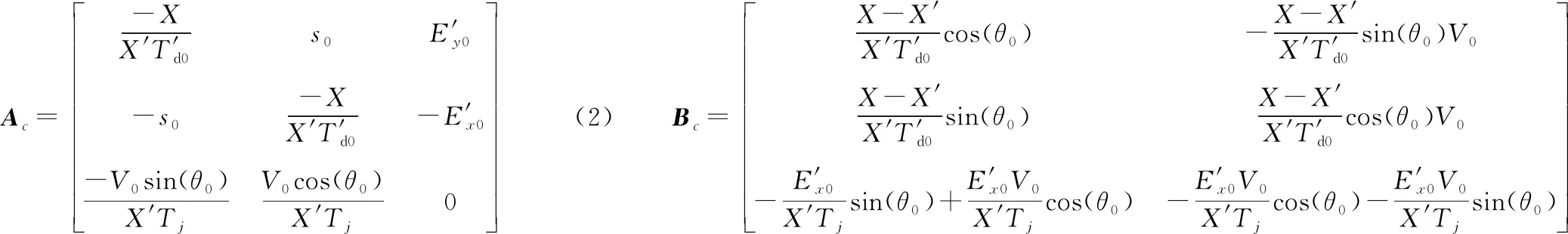
(3)

(5)

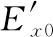
2 适用于负荷辨识的卡尔曼滤波方法

2.1 数据序列

PMU的采样周期为0.02 s，从PMU中获取长度为N的电压幅值序列V(k)，电压相角序列θ(k)，有功功率序列P(k)，无功功率序列Q(k)。首先进行数据预处理，包含去野值，筛选不良数据，去均值得到适合线性模型的数据。获得数据序列如下：

ΔV(k),Δθ(k),ΔP(k),ΔQ(k),k=1,2,…,N

2.2 基于卡尔曼滤波的负荷参数辨识方法

将如所示的连续状态空间模型转化成离散状态空间模型。

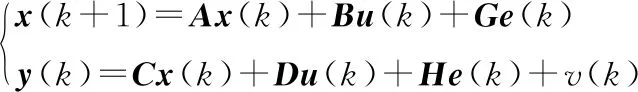
(6)

假定e(k)、v(k)为独立高斯白噪声序列，均值为0，用方差矩阵定义它们之间的关系，如式(7)所示。

E[e(k)eT(k)]=Q,E[v(k)vT(k)]=R,E[e(k)vT(k)]=0

(7)

式中:E为数学期望;Q为过程噪声协方差矩阵;R为测量噪声协方差矩阵。

传统卡尔曼滤波递推公式如式(8)所示。

(8)

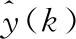
(9)

采用卡尔曼滤波存在以下问题:①R通常需要依照经验设定或仿真过程调整，难度较大；②最优估计高度依赖于精确线性动态系统模型和零均值高斯噪声的要求，在实际电网中难以满足。

2.3 改进的Sage-Husa自适应卡尔曼滤波计算方法

针对以上情况，本文将采用改进的Sage-Husa自适应卡尔曼滤波算法，Sage-Husa自适应卡尔曼滤波算法解决了当Q、R未知时如何进行估计的问题，然而会引起常值误差和滤波发散问题。因此，本文在负荷模型辨识中，选择固定过程噪声、更新测量噪声的改进方法。

基于以上改进方法，在如式(6)所示离散状态空间模型中，考虑更新测量噪声，则噪声的均值符合：E[e(k)]=0,E[v(k)]=r(k)，协方差矩阵符合：E[e(k)eT(k)]=Q,E[v(k)vT(k)]=R(k)。

自适应卡尔曼增益递推如式(10)所示。

(10)

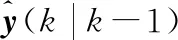
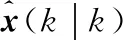
(11)

(12)

则卡尔曼增益阵

(13)

(14)

因此，利用递推式(10)和式(14)可交替估计状态参数和测量噪声。

3 浙江电网实际算例分析

将本文所提出自适应卡尔曼滤波算法应用于浙江电网220 kV华金变电站PMU数据。数据样本的起止时间是2019年11月21日14时0分0秒至14点2分0秒，总计120 s，采样频率为50 Hz，共6 000个数据点。依据经验选择参数上下限和初值。模型中Gc、Hc按照模型直接给出：

由于模型参数缺乏真实值对比，将数据集合分为辨识和验证两个部分以验证算法有效性。将0～20 s、40～60 s、80～100 s作为辨识参数数据，20～40 s、60～80 s、100～120 s作为验证参数数据。分别采用本文提出的自适应卡尔曼算法和传统卡尔曼算法对负荷模型进行辨识，参数辨识结果如表1所示。

表1 参数辨识结果

理想参数辨识结果应为初值附近波动的局部最优解，从表1中X、X′两项参数可以看出，对比2种滤波算法，传统方法在计算过程中多次触及参数上下限，不能得到可靠的估计值，而本文算法能够相对准确在局部跟踪参数。此外如表2所示，传统卡尔曼滤波算法辨识结果方差基本大于本文算法，且方差和的数量级更高，验证了本文算法的稳定性。

算法估计输出和真实输出的拟合度也是衡量算法是否满足实际应用要求的标准。两种方法在辨识数据集合0～20 s的有功功率和无功功率拟合度如图1和图2所示，在验证数据集合20～40 s的有功功率和无功功率的拟合度如图3和图4所示，在40～60 s和80～100 s数据段的拟合度因结果相似不再展开。

表2 参数方差

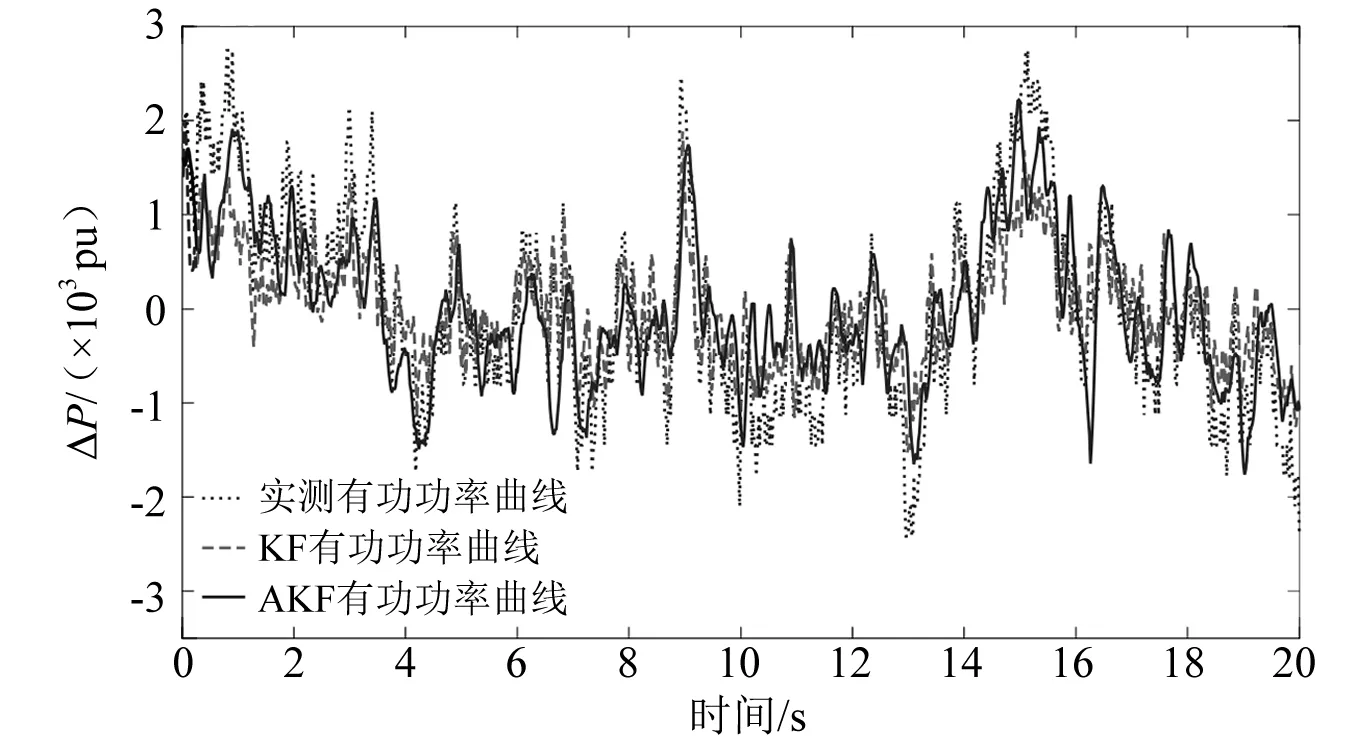
图1 辨识数据集有功功率拟合度

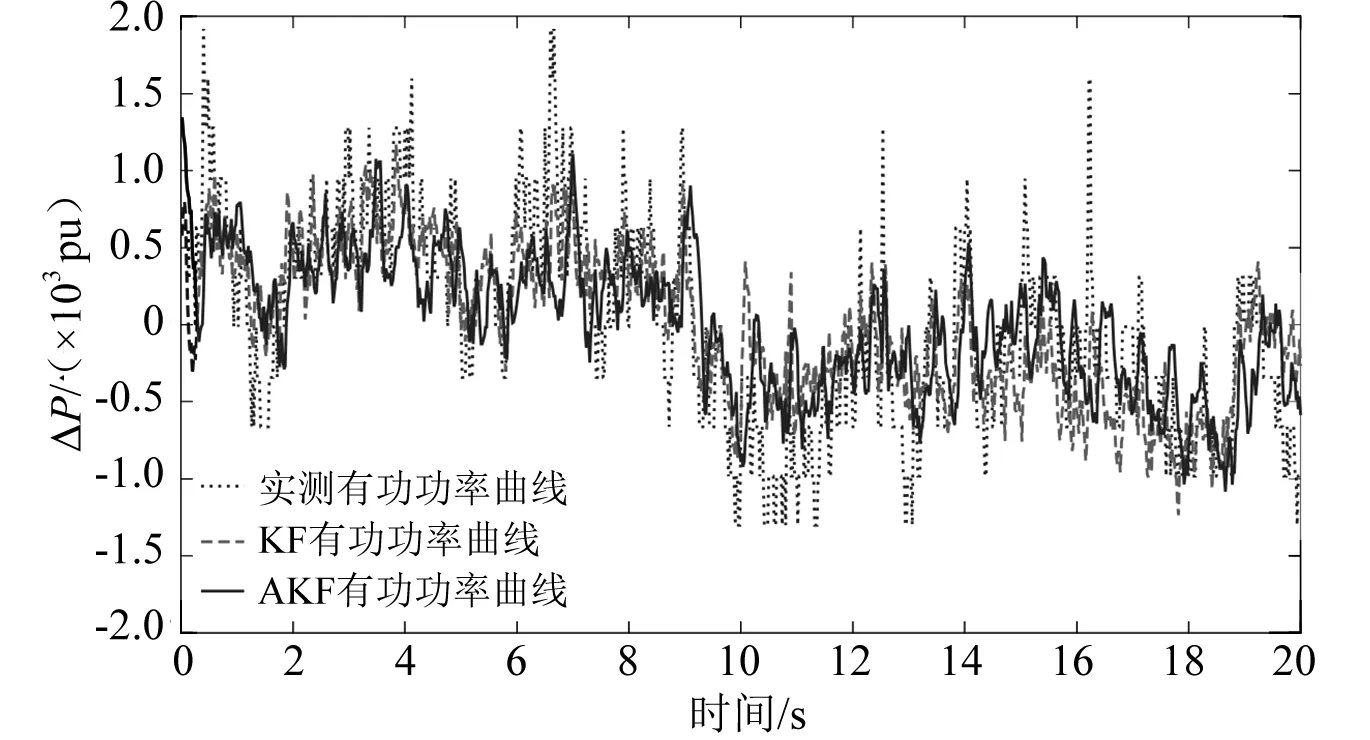
图2 辨识数据集无功功率拟合度

图3 验证数据集有功功率拟合度

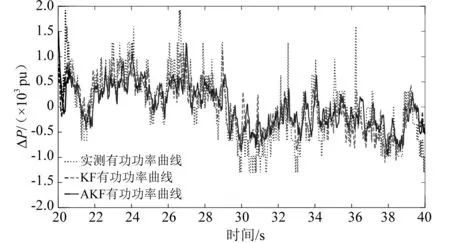
图4 验证数据集无功功率拟合度

4 结束语

本文考虑时变测量噪声，提出了一种基于自适应卡尔曼滤波的负荷模型参数在线辨识算法。浙江电网220 kV华金变电站实时运行数据的结果表明，本文提出的自适应卡尔曼滤波算法与传统卡尔曼滤波相比，能够得到更稳定可信的参数估计结果。下一步工作将考虑对更准确完整的模型和参数初值的确定方法进行研究，以提高参数在实际电力系统负荷中的可信度，提高计算效率。