通过分析矩阵乘法探索顶层算力提升

朱东辉，刘进锋

（宁夏大学信息工程学院，银川750021）

0 引言

世界上第一台通用计算机埃尼阿克（ENIAC）于1946年在美国宾夕法尼亚大学诞生后，人类世界因计算机的出而现发生了翻天覆地的变化。时至今日，计算机已深入人类生活的各个方面，我们接触到的计算机早已不同于埃尼阿克占地170平方米的庞大体积，现代计算机越来越小型化、高度集成化。在这个体积由大变小的过程中，计算机的计算能力伴随着其部件的小型化一直在增长。1975年，英特尔公司的创始人戈登·摩尔（Gordon Moore）提出了被称为摩尔定律的计算机硬件小型化趋势规律：集成电路上能容纳的晶体管数目每18个月可以增加一倍，也就是说，处理器性能每18个月可以增加一倍。然而随着这种小型化不断发展，半导体的物理极限即将到来，摩尔定律终归会走向失效[1]。

摩尔定律的终结会是计算机算力的终结吗？答案是否定的。现在的计算机应用对算力的要求是不断增长的，从图像识别、语音识别到自动驾驶、天气预报，都在算力提升的前提下蓬勃发展。如图1所示，计算机堆栈主要分为底层和顶层。底层硬件进步遭遇瓶颈的同时，顶层仍然存在着巨大的算力提升空间。在计算机堆栈顶层，软件、算法和硬件架构都将是算力提升的突破方向[2]。

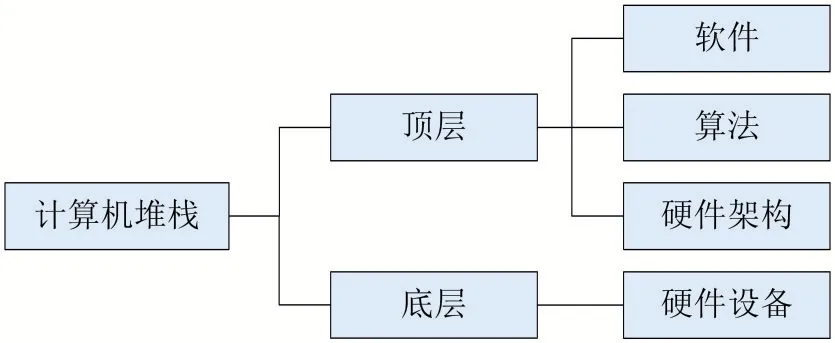
图1 计算机堆栈

矩阵乘法在各种信息处理技术中的应用十分普遍，它是实现图像处理、图像加密、云计算等技术的基础。自2012年以来，深度学习大放异彩，应用深度学习解决问题的方法层出不穷。作为深度学习的一个基础环节——矩阵乘法，尤其是大矩阵乘法，也受益于算力提升，其计算速度也在不断加快。本文以两个4096×4096元素值全为1的矩阵相乘作对比实验，分析不同编程语言、不同环境不同方法对计算速度的影响，进而探索在计算机堆栈顶层提升算力的可能性和方向。

1 算法描述

计算机中矩阵乘法虽有多种不同的实现方法，但其核心的原理是一致的。设矩阵A、B都为n阶方阵，结果矩阵为C，C=AB。C矩阵中元素的计算公式为：

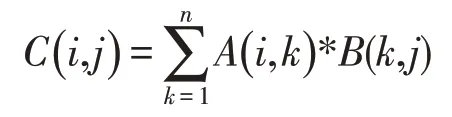
1.1 普通循环算法

普通循环算法是用三重循环直接计算A、B两个矩阵相乘，每次只计算出结果矩阵C中的一个元素。本文使用Python、Java、C这3种编程语言来实现矩阵相乘的普通循环算法，其核心代码为：

算法1普通循环算法

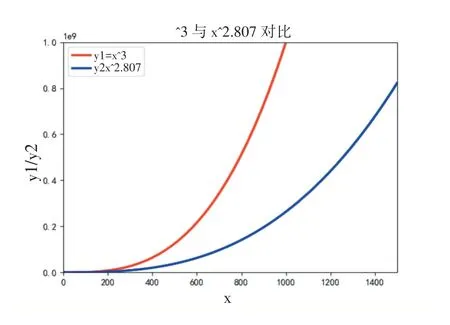
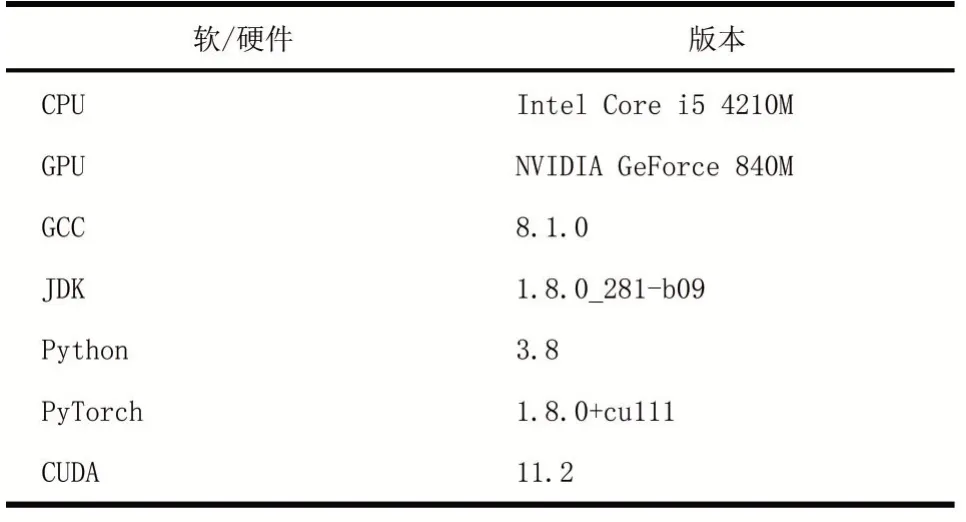
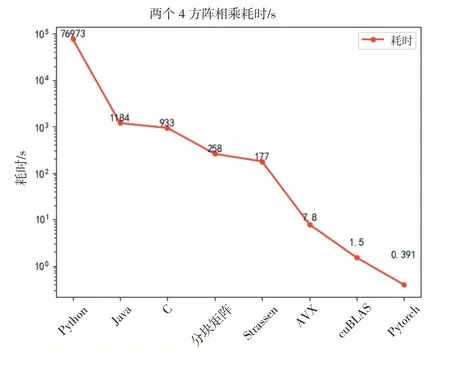
1.for（int i=0;i

2.for（int j=0;j

3.for（int k=0;k

4.C[i][j]+=A[i][k]*B[k][j];

普通循环算法在运行中进行了n3次迭代，每次迭代都在重复执行同样的计算，该算法时间复杂度为O(n3)。用单线程方式运行两个4096阶矩阵乘法的普通循环算法，Python 3.8耗时76973 s，Java耗时1184 s，C语言耗时933 s。使用Python实现的版本耗时超过21个小时，而Java和C语言的版本耗时都在20分钟以内。这数十倍的耗时差异给提升算力带来极大的动力，选择高效的编程语言就能大大节省时间成本。Python在简化编程的同时做了许多幕后工作增加了程序运行的时间；C语言和Java则更贴近底层，这两种方法用编程时的复杂换取更高的效率。

1.2 分块矩阵算法

将大矩阵分为一些较小的矩阵，先处理计算小矩阵，再将运算结果合并，这种方法在大矩阵的运算中是很常用的一种技巧。将大矩阵的乘-加运算转换为子矩阵的乘-加运算[3]。将矩阵分为q块执行分块矩阵乘法时，其伪代码如下：

算法2分块矩阵算法

1.输入：A（n*n），B（n*n），子块大小为（n/q）*（n/q）

2.输出：C（n*n）

3.begin

4.for i=0 to q-1 do

5.for j=0 to q-1 do

6.C（i，j）=0

7.for k=0 to q-1 do

8.C（i，j）=C（i，j）+A（i，k）*B（k，j）

9.endfor

10.endfor

11.endfor

12.end

此算法共执行了q3次矩阵乘法，每个矩阵乘法需(n/q)3次乘-加运算，总的乘-加次数为n3。使用分块矩阵的方法运行两个4096阶矩阵相乘耗时258 s。在双核四线程的处理器上分块矩阵的方法耗时缩短为C语言版的约1/4。

1.3 Strassen算法

Strassen算法是Volker Strassen于1969年提出的第一个时间复杂度低于O(n3)的矩阵乘法算法，其算法复杂度为O(nlog72)≈O(n2.807)[4-5]。如图2，由于幂函数的特性，Strassen算法在矩阵阶数超过300时，阶数越大其性能比普通循环算法的优势越明显。

图2 指数为3和2.807的幂函数图像

与分块矩阵算法类似，我们把大矩阵分割为数个子矩阵，再将其分别处理。Strassen算法以分治为核心思想，实现Strassen的伪代码如下：

算法3Strassen算法

1.if n=1 Output A×B

2.else

3.compute A11，B11，…，A22，B22%by computing m=n/2

4.P1 Strassen（A11，B12−B22）

5.P2 Strassen（A11+A12，B22）

6.P3 Strassen（A21+A22，B11）

7.P4 Strassen（A22，B21−B11）

8.P5 Strassen（A11+A22，B11+B22）

9.P6 Strassen（A12−A22，B21+B22）

10.P7 Strassen（A11−A21，B11+B12）

11.C11 P5+P4−P2+P6

12.C12 P1+P2

13.C21 P3+P4

14.C22 P1+P5−P3−P7

15.output C

16.end if

使用Strassen算法实现两个4096阶矩阵相乘耗时177 s，进一步缩短了处理矩阵相乘问题的时间。这种算法在计算中减少了乘法运算的次数，同时增加了加减法运算的次数，总体时间复杂度低于普通循环算法，时间复杂度的降低在计算阶数越大的矩阵乘法时越能体现出性能上高于普通循环算法的优势。

1.4 AVX指令集计算矩阵乘法

Intel AVX指令集（Advanced Vector Extensions，高级矢量扩展），增强了单指令多数据流的计算性能，同时也包含MMX/SSE指令集。该指令集与MMX/SSE的不同点在于AVX指令更加强大，它在指令的格式上发生了很大的变化，并加入了新的命令，实现了一些更加复杂的指令，提升了x86架构CPU的性能。

AVX指令集实现大矩阵乘法，其主要优势是将计算放入寄存器进行，本文中主要用到的数据类型和函数有[6]：

算法4AVX指令集主要数据类型及函数

1._mm256//包含8个float类型的256bit向量

2._mm256_setzero_ps（）//返回一个全0类型的float类型向量

3._mm256_loadu_ps（）//从未对齐的内存地址加载浮点向量

4._mm256_mul_ps（）//对两个float类型的向量进行相乘

5._mm256_add_ps（）//对两个浮点向量做加法

使用AVX指令集实现两个4096阶矩阵乘法耗时7.8 s。使用AVX指令集方法编程时，可直接在寄存器中进行元素读取，在底层硬件层面为计算进行提速。值得一提的是，编译时不使用O3优化的程序耗时48.8 s，经过O3优化耗时缩短至7.8 s。可见，编译时的优化也是算力提升的一个重要手段。

1.5 使用CUDA的矩阵乘法

CUDA（Compute Unified Device Architecture），是GPU制造商英伟达推出的GPU运算平台，它将CPU和GPU各自的优点相结合，释放出更好的计算机性能。在矩阵乘法的运算过程中，每次的运算都是相互独立的，并不依赖其他元素的运算，这是一个天然可并发的问题。在运算中可以将矩阵拆分并送至不同的块（block），每个块又包含多个线程（thread），然后进行运算得到结果矩阵中的元素值。

本文在安装英伟达显卡并支持CUDA的环境下，测试了PyTorch和cuBLAS两种方法来计算两个4096阶方阵乘法。

在PyTorch中，以Tensor形式存储矩阵mat1和mat2，再调用函数完成矩阵乘法运算，方可通过GPU为计算加速，使用PyTorch计算矩阵乘法的核心函数为：

算法5PyTorch算法

1.mat1=mat1.cuda（）

2.mat2=mat2.cuda（）

3.mat3=torch.mm（mat1，mat2）

cuBLAS库是在英伟达CUDA上实现BLAS（Ba⁃sic Linear Algebra Subprograms，基本线性代数子程序），它允许用户使用英伟达GPU的计算资源来加速计算。使用cuBLAS的函数可以方便地从GPU存取矩阵数据、分配内存单元以及矩阵运算[7]。

使用cuBLAS计算矩阵乘法主要使用的函数有：

算法6cuBLAS算法

1.cublasHandle_t handle

2.status=cublasCreate（&handle）//创建、初始化cuBLAS对象

3.cudaMalloc（）//分配GPU内存

4.cublasSetVector（）//将矩阵从CPU复制到GPU

5.cudaThreadSynchronize（）//同步函数

6.cublasSgemm（）//矩阵相乘

7.cublasGetVector（）//将结果矩阵从GPU复制到CPU

使用PyTorch、cuBLAS方法计算两个4096阶矩阵乘法耗时分别为0.39 s和1.5 s。对于矩阵乘法问题，GPU优势明显，短短的几秒钟就能完成运算。同是使用Python语言，PyTorch版比普通循环版运行时间缩短了19.69万倍，这种数量级的效率提高，是计算机堆栈顶层存在巨大算力提升空间的最好证明。

2 分析与对比

本文中的8种矩阵乘法的运行环境如表1所示。

表1 运行环境

本文通过8种不同的方法计算两个4096阶矩阵相乘，在程序运行时，对其核心即矩阵乘法部分进行计时。对比不同方法的运行时间，我们可以看到，最慢的是普通循环算法中的Python实现，用时超过21小时，而使用PyTorch+GPU方法则仅需0.39 s；同样是普通循环算法的Java和C语言则都用时远小于Python版本的，可见不同语言对顶层算力的提升的影响巨大。采用分块矩阵、Strassen等方法也能在时间上有很好的表现。PyTorch和cuBLAS方法使用GPU为计算加速，从硬件架构和软件优化两个方面同时提升算力，获得的效果十分显著。如图3所示，从耗时最多的Python实现普通循环算法到耗时最短的Py⁃Torch+GPU方法，速度缩短了19.69万倍，这样的提速意义非凡。

图3 不同方法实现4k乘法耗时变化

矩阵乘法在信息科学领域的应用十分普遍，发挥着不可替代的作用，针对实际应用情况选择合适的方法来实现高效的矩阵乘法至关重要。在矩阵很大时，尽量选择有GPU的设备并行计算；在算法上的优化还可以进一步降低时间复杂度，这对于大型矩阵的乘法运算有着巨大的意义，在Strassen的基础上，1990年，Coppersmith和Winograd提出的算法进一步将时间复杂度降低至O(n2.376)[8]，学者们基于C-W算法的研究还在逐渐降低矩阵乘法的时间复杂度，2012年Williams等人提出的方法时间复杂度已经小于O(n2.3727)[9]，算力的提升伴随着这样的研究还在继续；对性能要求很高的计算场合，应选择C语言这样贴近底层的计算机语言来提高效率，如果能和指令集、汇编语言混合编程，对整体性能提升会更多，Intel发布了AVX2和AVX512指令集，它们性能更加强大，可以进一步发挥计算机算力；编译时的优化也是提升性能的一个很好的方向，本文中AVX指令集实现矩阵乘法时用O3优化后运行时间又缩短了数倍，但类似的自动优化对规范编程的要求很高，编程人员可从编程的技巧和规范性上入手，使计算机算力更好地释放；使用CUDA实现的两个版本中，数据在内存和显卡存之间来回转储存在时间消耗，但内存和显存这类高速存取硬件让这部分时间非常短暂，在最新的硬件上，这个过程会更加短，可见，软件、算法和硬件结合能发挥计算机更多的计算潜力。

3 结语

后摩尔时代已经到来，以底层硬件的小型化作为实现算力的巨大提升的主要方向不再现实，而人类对算力的需求则越来越大，在硬件进步较慢的情况下，计算机堆栈顶层的算力还有很大的开发空间。正如本文所探索的，通过选用高效的方法从计算机堆栈顶层释放更大的算力空间。对于两个4096阶方阵乘法的计算时间，我们在同一台机器上实现了19.69万倍的提升，而这只是顶层算力空间开发的冰山一角，更多更好的潜力仍有待发掘。