故障火炮定向方法研究

郑兴博，刘爱峰，熊涛，赵楠，邹定美，秦鹏飞

(西北机电工程研究所，陕西 咸阳 712099)

直瞄和间瞄是现代自行压制武器系统所具备的两种作战方式。当目标可见且符合直瞄射击条件时，自行压制火炮在半自动或者手动方式下调炮，使用直瞄镜对目标进行瞄准并激光测距，根据测得的炮目距离计算出射击装定诸元，在自动方式下调炮到位；当目标不可见时，需间接瞄准射击，由指挥系统下达射击装定诸元或者根据炮目坐标解算出装定诸元，在自动方式下进行调炮到位[1-2]。压制火炮都配备了精度较高的定位定向装置，可实时获得炮塔轴线的指向，通过操瞄得到火炮身管轴线的实际指向。当定位定向系统发生故障时，压制火炮无法自主进行定向，不能获得操瞄所需的炮塔身管轴线北向角，也就不能实现间瞄作战的功能。

现已存在大量针对定位定向装置失效的火炮进行定向的方法研究。在传统情况下，采用瞄准点法、标杆法或者方向盘法[3-4]对定向功能故障的压制火炮赋予基准射向，即为故障火炮炮塔轴线赋予已知北向角。研究表明，这些方法都能为故障火炮实现定向功能，然而在实际使用中，这些传统方法存在较多的缺陷，例如人员在炮车外操作，战场防护性差；操作前的准备工作较为繁琐，所需时间长[5-7]；需单独配备测地保障分队，在实际作战中难以确保，并且增加了成本。通常情况下，压制武器系统都是数门同时参与作战，当出现定向功能故障的火炮时，可使用现有的正常火炮对故障火炮进行定向。充分利用了战场中现有的条件，不需要额外增加人员和设备。

1 基本坐标系定义

压制火炮定位定向装置获得的是大地坐标系[8]下的参数值，而随动系统使用的是火炮自身坐标系下的参数值，需对大地坐标系下的数据进行转换得到火炮自身坐标系下的数据。

自行压制火炮涉及的坐标系定义如图1所示。

定义1地理坐标系{Od，Xd，Yd，Hd}。地理中规定的当地坐标系，其中坐标轴Xd指向大地正北向，Yd指向大地正东向，Hd铅垂向上[9]。

定义2大地坐标系{O0，X0，Y0，H0}。与地理坐标系处于同一水平面，以正常火炮所在点为原点建立的坐标系，其中坐标轴O0X0指向大地正北向，O0Y0指向大地正东向，O0H0铅垂向上。

定义3炮耳轴坐标系{O1，Xp，Yp，Hp}。O1为炮塔回转中心，与大地坐标系原点存在一定高度差，坐标轴O1Xp指向炮塔轴线方向(炮塔轴线是当火炮身管高低角为0°时的身管轴线)，O1Yp指向炮塔耳轴方向，O1Hp垂直于炮塔平面，向上为正。

定义4身管轴线O1S。

定义5参考坐标系{O1，X1，Y1，H1}。将大地坐标系沿O0H0向上平移至O0和O1重合时构造的坐标系，便于分析计算。

定义6炮塔平面横倾角θ0，右倾为正；炮塔平面纵倾角Ψ0，前倾为正。高低受信仪值ε0，即身管轴线和炮塔轴线之间的夹角。

定义7炮塔轴线北向角α0，炮塔轴线在大地坐标系下的投影和基准北向的夹角；身管轴线北向角λ0，身管轴线在大地坐标系下的投影和基准北向的夹角。

2 赋予基准射向

2.1 正常火炮身管轴线定向

在图1中，定位定向功能正常的压制火炮，用直瞄镜[10]瞄准目标物时，通过定位定向装置实时获取炮塔轴线北向角α0，安装在炮塔上的姿态传感器实时获取炮塔平面的横倾角θ0和纵倾角Ψ0，高低受信仪获取身管轴线相对炮塔轴线的夹角ε0，可计算得到火炮身管轴线北向角λ0为

λ0=α0+arctank,

(1)

直瞄镜瞄准后进行激光测距得到的火炮和目标之间的距离为l0，则可根据坐标转换[11]计算求得炮目距离在大地坐标系下的投影，即l0在O0X0Y0中的投影为

l01=l0cos[arcsin(cosε0sinΨ0+

sinε0cosθ0cosΨ0)].

(2)

不考虑火炮横倾和纵倾限制的情况下，火炮身管轴线和炮塔轴线在大地坐标系中的位置可能存在多种情况，如图2所示。

在图2中，火炮炮塔轴线和身管轴线在大地坐标系O0X0Y0面中的投影，可分布在水平面中任意象限中，需对式(1)进行调整。

表1 第1象限情况下身管轴线的参数

身管轴线北向角的取值范围为[0,2π]，需对λ0进行规整，规整后的身管轴线北向角如表2所示。

表2 第1象限情况下身管轴线北向角

同理，分析可得到炮塔轴线位于第2、3和4象限时，身管轴线规整后的北向角，如表3所示。

表3 身管轴线北向角

根据以上分析，进一步对身管轴线北向角计算公式进行规整，得到计算身管轴线北向角的通用公式。

令cosε0cosΨ0-sinε0cosθ0sinΨ0=δ,

(3)

式中，λδ为中间值。

则身管轴线北向角λs为

(4)

式(3)和式(4)是不考虑火炮横倾和纵倾限制时身管轴线的计算公式，在实际作战[12]使用时，火炮横倾和纵倾有一定的限制，即式(3)中δ始终是大于0，可进一步将式(4)调整为

(5)

因此，在实际中，可利用式(1)和式(5)实现对正常火炮身管轴线的定向。

2.2 赋予故障火炮基准射向

正常火炮通过对准可获得基准射向，再通过坐标转换的计算可以求出身管的北向角。当定位定向装置故障时，炮塔轴线的北向角未知，即不能确定基准射向。

使用正常火炮对故障火炮进行定向，需首先选定合适的标志物。如图3所示，在参考坐标系中，O1点为正常火炮所在点，A点为故障火炮所在点，B点为选取的标志物所在点。

1)正常火炮定位定向装置对准之后，进行调炮并使用直瞄镜瞄准故障火炮，进行激光测距，获得两炮之间的斜距离，即图3中的l1；正常火炮姿态传感器获得炮塔平面横倾角θ1和纵倾角Ψ1，高低受信仪值ε1，炮塔轴线北向角为α1。

由式(1)和式(2)可以计算得到：

(6)

l10=l1cos[arcsin(cosε1sinΨ1+sinε1cosθ1cosΨ1)].

(7)

按照式(5)进行规整，可得到身管轴线北向角为

(8)

2)正常火炮进行调炮并使用直瞄镜瞄准标志物，进行激光测距，获得炮物之间的斜距离，即图3中的l2；同样获得炮塔平面横倾角θ2和纵倾角Ψ2，高低受信仪值ε2，炮塔轴线北向角为α2。

同理，由式(1)和式(2)可以计算得到：

(9)

l20=l2cos[arcsin(cosε2sinΨ2+sinε2cosθ2cosΨ2)].

(10)

同理，按照式(5)进行规整后得到的身管轴线北向角为

(11)

3)对于△A0O1B0，依据三角形法则可以计算得到l30，即故障火炮到标志物之间的距离在大地坐标系的投影：

(12)

4)故障火炮调炮并使用直瞄镜瞄准标志物，故障火炮和标志物之间的位置有多种情况。当λ2s>λ1s时，两炮和标志物的两种位置关系如图4、5所示。

可计算出故障火炮身管轴线北向角中间量为

(13)

当λ2s≤λ1s时，式(13)同样适用。

将λ3δ规整至[0,2π]，得到故障火炮瞄准标志物时,火炮身管轴线北向角为

(14)

5)故障火炮瞄准标准物时，获得炮塔平面横倾角θ3和纵倾角Ψ3,高低受信仪值ε3，可计算出故障火炮炮塔轴线北向角中间量为

(15)

对α3δ在[0,2π]内进行规整，得到炮塔轴线北向角，即基准射向为

(16)

通过上述方法，即可赋予定位定向装置故障的火炮基准射向。

3 方法实现及其优势

笔者提出利用正常火炮的定向功能和直瞄测距功能来赋予故障火炮基准射向。该方法操作简单,仅需现有的装备即可快速完成。

3.1 方法实现

本文中方法的实现需要火炮的瞄具和瞄准手终端。瞄具由带有激光测距功能的直瞄镜组成，瞄准手终端具有通信模块、显示模块和解算软件，其中解算软件包由采集模块和计算模块组成，采集模块的主要功能是采集相关数据；解算模块是将第2节中的方法以代码的形式实现在瞄准手终端中，用于解算出基准射向。

赋予故障火炮基准射向的时间为

tw=t0+t1+t2+t3+t4,

(17)

式中：tw为赋予故障火炮基准射向所需的时间；t0为正常火炮瞄准故障火炮进行激光测距并采集数据的时间；t1为正常火炮瞄准标志物进行激光测距并采集数据的时间；t2为故障火炮瞄准标志物并采集数据的时间；t3为正常火炮将相关数据发送给故障火炮的时间；t4为故障火炮瞄准手终端进行解算的时间。

分析可知，正常火炮定位定向对准之后，赋予故障火炮基准射向的时间大约在2 min以内。

3.2 精度分析

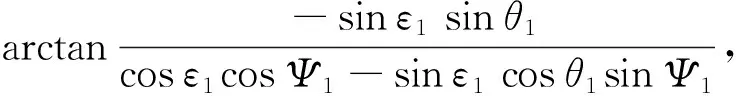
设：

n1=cos[arcsin(cosε1sinΨ1+sinε1cosθ1cosΨ1)],

n2=cos[arcsin(cosε2sinΨ2+sinε2cosθ2cosΨ2)].

由于本文方法中使用的三角函数具有周期性，并且式(8)中规整的各种情况对最终的精度影响没有差别，选取0<λ10<2π、l10≤l20的情况进行分析，即：

λ3δ=α1+m1+Q,

(18)

式中，

(19)

理想情况下，计算出的故障火炮基准射向误差为0，但在实际中，火炮定向装置、激光测距仪、姿态传感器和高低受信仪均存在误差。分别分析各种误差对最终精度的影响。

3.2.1 正常火炮定向误差

正常火炮瞄准故障火炮和标志物时，获得的炮塔轴线北向角α1和α2均存在误差，分别为Δα1和Δα2。该定向误差仅影响λ3δ，令Δα=Δα2-Δα1，将误差代入式(18)，可得

λ3δ=α1+Δα1+m1+Q′,

(20)

式中，

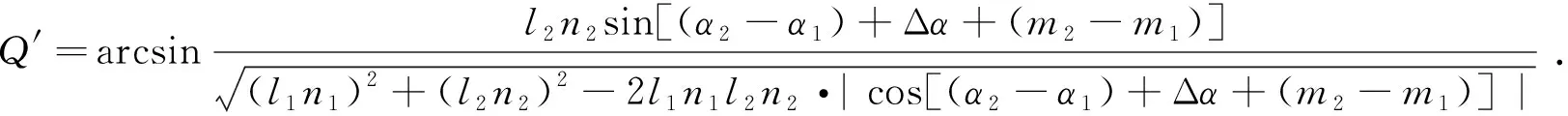
(21)

由于定向装置的误差在1 mrad以内，所以-1 mrad<Δα1<1 mrad，-2 mrad<Δα<2 mrad，因此Δα≪α2-α1，即当存在定向误差时，Q≈Q′，因此λ3δ的变化仅由Δα1引起。

由上述分析可知，因定向装置误差引起的故障火炮基准射向精度在1 mrad以内。

3.2.2 激光测距误差

激光测距仪的测量距离为200～5 000 m以内，误差-5 m<Δl<5 m，测距误差仅影响λ3δ，将误差代入式(18)，则

λ3δ=α1+m1+Q″,

(22)

式中,

(23)

3.2.3 姿态传感器和高低受信仪误差

横倾值、纵倾值和高低受信仪值影响m1、m2、m3、n1和n2。

横倾和纵倾姿态传感器的测量范围均为-100～100 mrad，测量误差-0.5 mrad≤Δθ≤0.5 mrad、-0.5 mrad≤ΔΨ≤0.5 mrad；高低受信仪测量范围-2°～78°，测量误差-20″≤Δε≤20″。

由于横倾误差、纵倾误差和高低受信仪误差较小，对m1、m2、m3、n1、n2的影响同样较小，因而由这些测量误差引起的故障火炮定向误差可以忽略。

经过分析可知：赋予故障火炮基准射向的精度近似于正常火炮的定向精度，满足压制火炮定向精度要求。

3.3 与传统的方法对比

本文方法与传统的瞄准点法、方向盘法和标杆法的对比如表4所示。

表4 本文方法和传统方法的比较

根据表4可知，传统方法都需要额外的测地保障分队，增加了作战成本，人员缺乏防护，易受战场环境限制，操作时间较长；笔者所提出的方法充分利用全连现有的装备进行，所有操作均在自行火炮内进行，安全性高、不受战场环境限制，整个过程在2 min以内，故障火炮基准射向精度仅受正常火炮定向精度影响，误差不大于1 mrad。

本文压制火炮激光测距范围为200～5 000 m，故本文方法适用于炮目距离在200～5 000 m范围内。

4 结束语

笔者研究了一种赋予定位定向装置故障的压制火炮基准射向的新方法。首先根据实际的战场环境，选择合适的标志物；使用已对准的正常火炮瞄准故障火炮并进行激光测距，同时采集炮塔平面横倾角和纵倾角、高低受信仪值，以及炮塔轴线北向角；同样的方法瞄准标志物并采集数据，根据三角形法则可解算出故障火炮到标志物的直线距离并发送给故障火炮；故障火炮瞄准标志物采集数据，解算得到自身基准射向。本研究充分发挥了压制武器系统的功能，省掉了传统方法所需的测地保障分队，并且人员操作安全，误差与正常火炮定向误差基本相同，能快速、精确地赋予故障火炮基准射向。