考虑堵片影响的筒式武器后喷流场研究
2021-09-23丁宁郭保全常亚李鑫波朱家萱
丁宁,郭保全,常亚,李鑫波,朱家萱
(1.中北大学 机电工程学院,山西 太原 030051;2.中北大学 火炮技术研究中心,山西 太原 030051)
筒式武器在击发后,瞬间生成大量火药燃气,火药燃气冲破后喷堵片从喷管尾部流出,在后方形成复杂的气固耦合流场,并伴随有高冲击波、高温火焰、高速堵片等危险现象,对炮手安全造成极大的隐患[1-3]。研究筒式武器后喷流场对优化筒式武器安全性能,保证炮手安全具有重要意义,因此,近年来得到了相关学者广泛关注。
目前,国内外学者采用仿真分析和试验分析的方法对筒式武器后喷流场开展了大量研究。庞春桥等[4]通过试验的方法测试了某无后坐炮的后喷超压、热流等,并结合概率模型得到了人员在不同危险源作用下的创伤概率。张磊等[5-7]研究了单兵筒式武器液态平衡发射过程,通过仿真和试验验证了液态平衡体对尾喷流场的消焰、消烟、降噪作用。王杨等[8]研究了无后坐炮整个流场的发展过程,以及火炮超压峰值分布特点。马宏伟[9]通过解析解法和试验的方法研究了反坦克火箭筒在发射后堵片的后抛速度,并提出了减少后喷危险界的可行方法。但是,国内外学者在对筒式武器后喷流场数值仿真研究时,一般对后喷堵片作出忽略假设,不考虑其对后喷流场的影响。
笔者采用Ansys Fluent流体计算软件,建立筒式武器后喷流场仿真模型,采用6DOF动网格技术,研究了筒式武器在不同破膜压力、不同堵片质量等条件下发射时后喷流场冲击波压强变化规律以及堵片运动规律。本文内容对进一步研究筒式武器后喷流场规律和界定炮手危害区具有一定指导意义。
1 计算模型
1.1 基本假设
由于筒式武器后喷流场的复杂性,作出以下假设:
1)将实际三维模型简化成二维轴对称模型;
2)高温高压火药燃气作为理想气体考虑;
3)单兵筒式武器整个发射过程在很短时间内进行,不考虑火药燃气和喷管壁面的热量交换;
4)堵片在喷管喉部发生剪切断裂,整个从喷管尾部喷出;
5)不考虑重力对堵片运动的影响。
1.2 数学模型
流场求解的控制方程由连续方程、动量方程和能量守恒方程组成[10]。
1.2.1 连续性方程
对于二维圆柱坐标系中,连续性方程为
(1)
式中:ρ为燃气密度;u为轴向速度;v是径向流速。
1.2.2 动量守恒方程
对于二维轴对称几何外形,轴向和径向的动量守恒方程组为
(2)
(3)
式中:fx为质量力f的x方向的分量;fr为质量力f的r方向的分量;μ为燃气的黏性系数;μ′为燃气的第二黏性系数;V是燃气的速度矢量;p为燃气的压力。
1.2.3 能量守恒方程
(4)
式中:T为温度;k为传热系数;sT为流体热能源。
1.2.4 湍流模型
笔者采用的k-ε湍流模型的控制方程为
Gk+Gb-ρε-YM,
(5)
(6)
式中:Gk为平均速度引起的的湍动能产生;Gb为浮力引起的湍动能产生;YM为可压湍流脉动造成的耗散率;C1、C2、C1ε、C3ε均为常量。
1.3 网格划分
笔者采用了结构网格动态分层技术,并结合6DOF动网格求解方法,对后喷流场和堵片运动规律进行求解。计算模型示意图如图1所示。int_1、int_2通过interface滑移边界与int_3交接,int_1与int_2通过共节点的方式交接。int_2为动网格区域,在动网格中设置passive,跟随堵片运动,internal-bot为网格分裂区,internal-top为网格坍塌区。当动边界拉伸相邻网格满足式(7)时,internal-bot层分裂一层网格;当动边界压缩相邻网格满足式(8)时,internal-top层将合并一层网格。
h≥(1+αs)hideal,
(7)
h≤αchideal,
(8)
式中:hideal为理想网格高度;αs为分裂因子;αc为坍塌因子。本文轴向网格均匀划分为2 mm,hideal取2 mm,αs取0.4,αc取0.2。
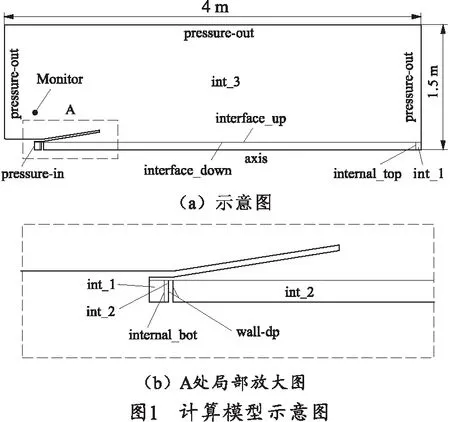
计算网格如图2所示,网格总数在50万左右。
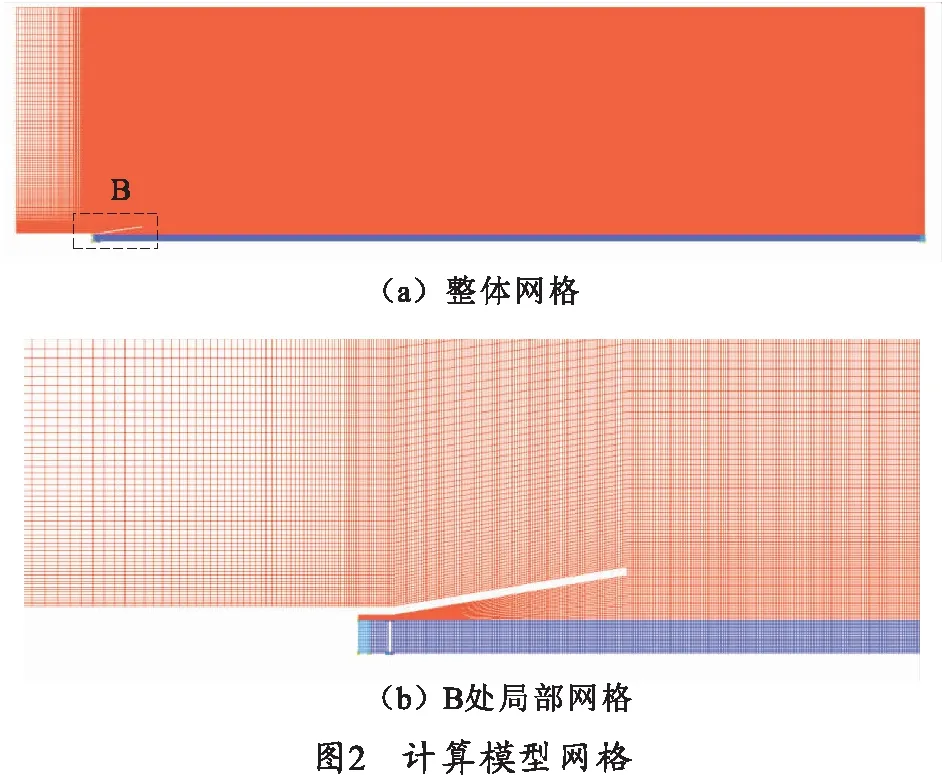
1.4 边界条件及算法
以某82 mm筒式武器内弹道数据为入口边界条件,如图3所示。
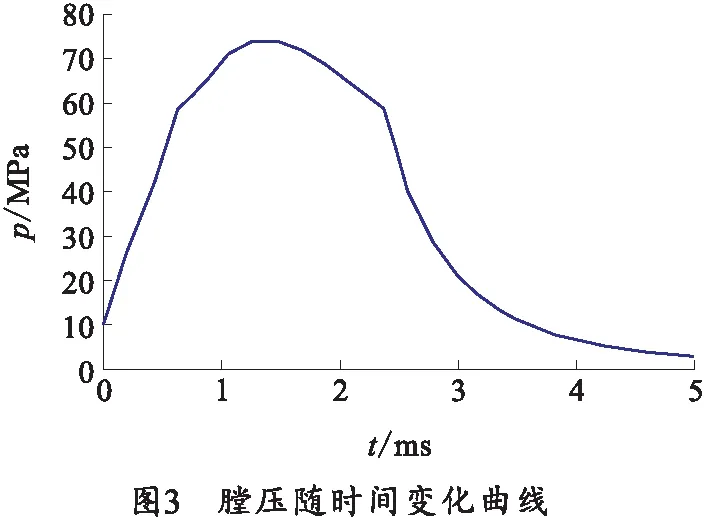
出口压力取1个大气压,出口温度取300 K;壁面函数采用标准壁面函数,壁面不考虑热量交换;求解方法采用基于压力的耦合求解方法,对二维控制方程的离散采用有限容积法,对导数项采用二阶迎风格式,控制方程中的湍流模型采用k-ε模型。
仿真计算从堵片断裂完成后开始,因此在对计算域进行初始化时分两步处理。首先域压力取1个大气压,温度取300 K,进行标准初始化。之后通过patch的方法将堵片前端区域压强设置为破膜压力。
2 仿真结果及分析
以某82 mm筒式武器为研究对象进行计算,破膜压力取10 MPa,堵片质量取30.5 g。为保证网格在运动过程中不出现负体积,时间步长选取应满足
hideal>vt,
(9)
式中:v为动网格运动速度;t为时间步长。计算时间步长取2 μs,共计算3 000步。
根据堵片在后喷流场中受到的火药燃气推力作用和前传激波阻力作用的变化,堵片在后喷流场中的运动可分为3个阶段:加速运动阶段、稳定运动阶段和减速运动阶段。
2.1 堵片加速运动阶段
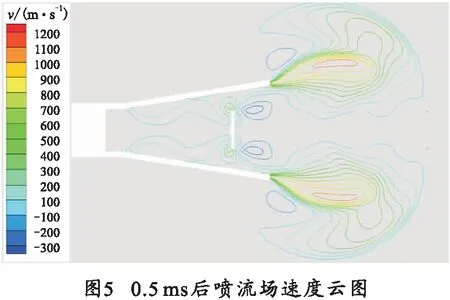
图4~7描述了堵片在加速运动阶段的后喷流场变化。筒式武器在点火后,药室内的压力迅速上升到破膜压力,堵片断裂,堵片开始加速运动。由图4可知,在堵片前方形成一个较大的前传激波。同时,火药燃气与堵片作用会产生一个指向后方的后传激波。由图5可知,此时火药燃气速度很快,部分火药燃气冲破堵片,从喷管喷出;并在出喷管后沿喷管径向压缩空气,形成一系列较弱的激波。
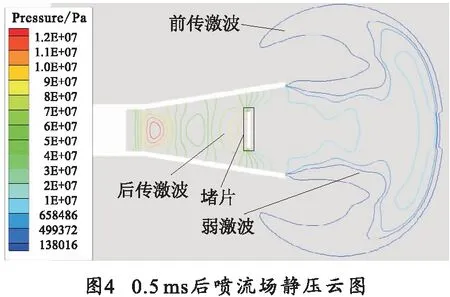
在0.6 ms左右堵片喷出喷管,后喷流场变化如图6、7所示。堵片速度达到590 m/s。此时前传激波开始进入三维膨胀阶段,呈球形迅速扩大。堵片前的一系列弱激波受到堵片运动和火药燃气作用,逐渐形成一道较强的激波继续向前运动。0.6—0.7 ms,堵片受火药燃气推力作用继续做加速运动,速度峰值为670 m/s。


2.2 堵片稳定运动阶段
图8、9描述了堵片在稳定运动阶段后的喷流场变化。
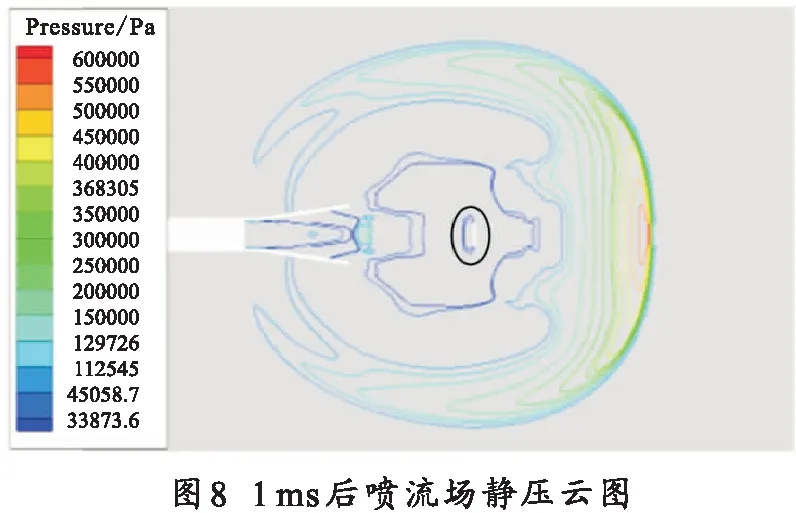

由图8、9可知,堵片在此阶段受火药燃气推力作用和前传激波阻力作用近似平衡,堵片前端面和后端面压强差值较小,此时堵片速度变化不大,堵片速度保持在650 m/s左右。
2.3 堵片减速运动阶段
图10、11描述了堵片在减速运动阶段的后喷流场变化。随着前传激波在空间膨胀,激波运动速度下降,而堵片仍以较快的速度往前运动,堵片逐渐穿过前传激波,因此在堵片前端生成一个较高的激波阻力,堵片速度开始有明显的下降。


3 堵片参数分析
3.1 不同堵片质量条件下的流场变化
图12描述了筒式武器在不同堵片质量下发射时近场压强变化曲线。高压峰值出现在1.5—2.0 ms之间,堵片质量越大,第1个压强峰值越高,但由于质量变化幅值不大,所以压强峰值变化不明显。第2峰值出现是由堵片前端形成的弱激波引起的。堵片质量越小,运动速度越快,堵片前端的弱激波强度更高。因此堵片质量越小,第2个压强峰值出现时间点越靠前,峰值越高。当堵片质量为15.3、22.9 g时,第2个压强峰值高于第1个压强峰值。所以,在一定堵片质量范围内,使用质量较大的堵片可以避免出现近场压强高峰。

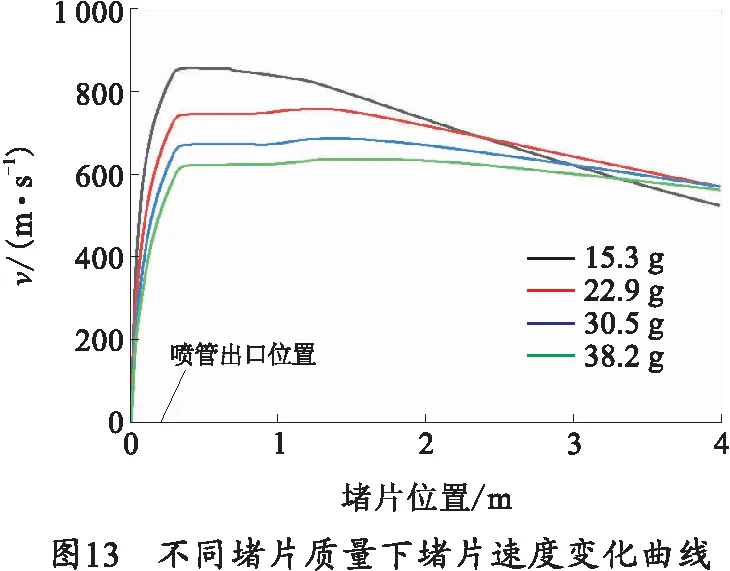
图13描述了筒式武器在不同堵片质量下发射时堵片速度变化曲线。堵片在出喷管后仍然受到火药燃气的推力作用处于加速阶段;之后,堵片受到燃气推力作用和前传激波阻力作用近似平衡,堵片速度不再增加;而当堵片速度高于激波运动速度时,堵片开始穿过前传激波,堵片受激波阻力影响增大,堵片速度开始明显下降。堵片质量越大,速度峰值越低,同时堵片在稳定运动阶段运动时间越长。
3.2 不同破膜压力条件下的流场变化
图14描述了筒式武器在不同破膜压力下发射时近场压强变化曲线。破膜压力对第1个压强峰值影响较小,但破膜压力越高,火药燃气射流从堵片侧边流出速度越快,对堵片前端弱激波压缩更剧烈,形成的激波更强,使第2个压强峰值越高。
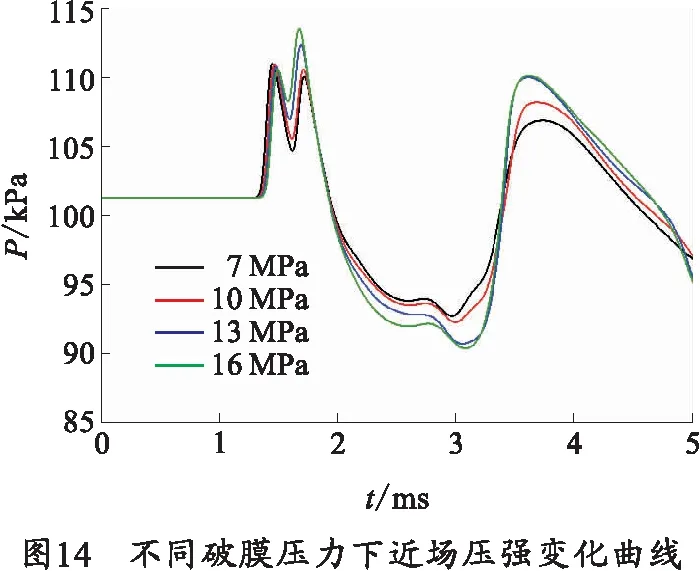
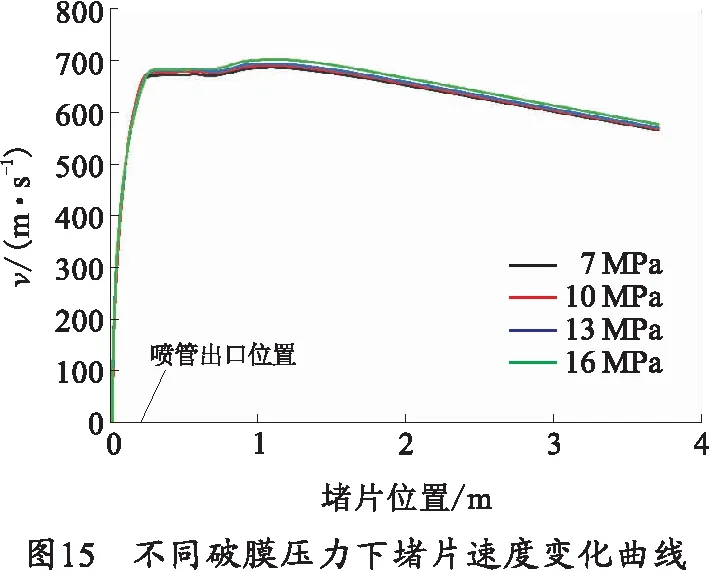
图15描述了筒式武器在不同破膜压力下发射时后抛堵片速度曲线。随着破膜压力升高,堵片初始受到的火药燃气的推力就更大,从而使堵片速度呈上升趋势。
4 结论
笔者以某筒式武器为研究对象,研究了其在不同堵片质量、不同破膜压力条件下发射时,筒式武器的后喷流场变化规律和堵片运动规律,得出以下结论:
1)堵片在后喷流场中的运动可分为加速运动阶段、稳定运动阶段和减速运动阶段;在堵片质量为30.5 g、破膜压力为10 MPa条件下,堵片速度峰值在670 m/s左右。
2)随着堵片质量增加,堵片速度明显减少,近场压强第1个峰值有减小趋势,第2个峰值有明显增大趋势。
3)随着堵片破膜压力增加,第1个压强峰值变化较小,第2个压强峰值明显增大,堵片速度有上升趋势。
