合取布尔网络的能观性

丁路青，李睿

（大连理工大学数学科学学院，大连116024）

0 引言

为了深入研究生物遗传机理，20世纪60年代末Kauffman提出使用布尔网络模型刻画细胞和基因调控网络的理论，用二进制1（转录）和0（不转录）表示基因的两种转录状态，它们之间的相互作用通过以布尔函数形式给出的逻辑规则表示。布尔网络模型是模拟网络动态过程的基本框架，尤其是在生物背景下，该模型已经有了丰富的理论成果[1-3]。

程代展教授及其团队提出使用矩阵半张量积研究布尔网络，这个方法的基本思想是把布尔网络转化成一个离散时间线性系统，使布尔网络的表示代数化，形式变得简单[4]，从而能够使用许多可用于线性状态空间模型的标准数学工具，进而有助于在理论框架内研究布尔网络模型，为后续研究奠定了一个合理的基础，获得了一系列优秀的研究成果[5-25]。

合取布尔网络是布尔函数值的更新规则仅包含and算子的一类特殊布尔网络，有着较好的性质[26-28]，故对其研究受到特别的关注。文献[29]研究了合取布尔网络的轨道控制和状态控制集，给出集合是网络控制集的充要条件和确切的控制规则。文献[30]考虑寻找直接影响输入的最小状态变量集，使最终的合取布尔网络能控，给出了能控的充要条件和用于检测能控性的算法，并证明了合取布尔网络的最小能控性问题是NP难的。文献[31]研究了合取布尔网络的最小能观性问题，给出了具有多项式复杂度的最小能观性判断算法。

布尔网络的能观性是研究布尔网络的一个重要方向，若研究基于矩阵半张量积方法[32-34]，对有n个状态变量能观性的判断是在矩阵阶数为2n×2n的基础上开展的。文献[35]是基于图理论方法研究的能观性，给出了判断能观性的充要条件，同时证明合取布尔网络的能观性问题是NP难的。

本文第一部分是对基础知识的回顾，介绍了具有n个状态变量，m个输出的布尔网络的表示形式，给出布尔网络邻接矩阵的定义，利用已有结论，把状态变量随时间变化的信息转移到矩阵的变化上。第二部分先定义了邻接矩阵和状态变量之间的运算，建立了状态变量和邻接矩阵之间的联系，进而把状态变量用邻接矩阵和下一时刻的状态变量表示出来，给出了用关键矩阵判断网络在[0，N]上能观的充要条件并给出例子验证。第三部分研究了具有强连通图的合取布尔网络的能观性，给出了判断其能观性的充要条件。最后一部分是总结。

1 预备知识

1.1 布尔网络模型

具有n个状态变量，m个输出的布尔网络表示为：

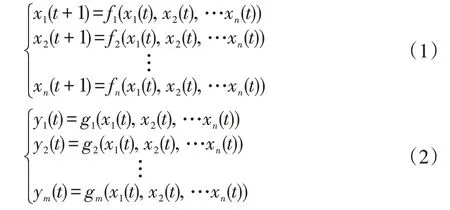
其中xi∈{0，1}，yj∈{0，1}，yj表示输出，fi:{0，1}n→{0，1}，f=（f1，f2，…，fn）T称为布尔函数或逻辑函数，gj:{0，1}n→{0，1}，g=（g1，g2，…，gm）T称为输出函数，这里i=1，2，…，n；j=1，2，…，m。

1.2 邻接矩阵和能观性

定义1.1定义网络（1）的邻接矩阵A=（aij）n×n，其中：

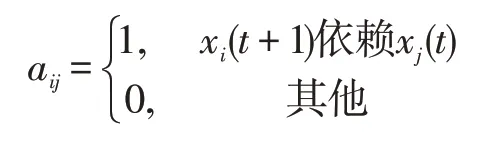
类似的可以定义输出函数的邻接矩阵，B=（bij）m×n，其中：

定义1.2如果布尔网络的函数仅是AND算子“∧”，则称该布尔网络为合取布尔网络。

假设以下涉及的布尔网络都是合取布尔网络。由状态变量的取值可以知道xi∧xi=xi，xi∈{0，1}，为方便记x1∧x2∧…∧xn=∧j∈{1，2，…，n}xj以下叙述中省略算子“∧”。下面先给出网络在[0，N]上能观的定义。

定义1.3对上述布尔网络，设t时网络的状态x（t）=（x1（t），x2（t），…，xn（t））T，输出y（t）=（y1（t），y2（t），…，ym（t））T，称网络在[0，N]上是能观的，如果对任意两个不同的初始状态x（0），x(0)产生两个不同的输出序列{y（0），y（1），…，y（N）}，{y(0)，y(1)，…，y(N)}。

注：在[0，N]上能观意味着对任意给定的输出序列{y（0），y（1），…，y（N）}总能唯一地确定出初始状态x（0）。

例1.1考虑合取布尔网络在[0，1]上的能观性。

（1）若输出为y1（t）=x1（t），则该网络在[0，1]上能观：给定{y（0），y（1）}={y1（0），y1（1）}，因为y1（0）=x1（0），y1（1）=x1（1）=x2（0），这意味着输出{y（0），y（1）}能唯一地确定原始状态x（0）=（x1（0），x2（0））T，因此网络在[0，1]上能观。

（2）若输出为y1（t）=x2（t），则该网络在[0，1]上不能观：给定{y（0），y（1）}={y1（0），y1（1）}，因为y1（0）=x2（0），y1（1）=x2（1）=x1（0）x2（0），若取x2（0）=0，那么x1（0）取任意值都会使输出相同，因此网络在[0，1]上不能观。

由上例可见网络是否能观与输出函数的选取有关。观察网络（1）可以发现t+1时的状态依赖t时的状态，t时的状态依赖t−1时的状态，…，这些依赖关系可以由布尔函数多次复合得到，也即是状态变量随时间的变化表现到布尔函数的多次复合上。接下来定义邻接矩阵之间的运算，使布尔函数的复合对应到邻接矩阵的运算上，即给出函数复合与矩阵运算之间的关系。

1.3 已有结果

定义1.4设A=（aij）n×n，B=（bij）n×n是两个合取布尔网络的邻接矩阵，定义A⊗B=（cij）n×n，其中cij=max{ai1b1j，ai2b2j，…，ainbnj}。

可以验证上述定义有意义，参见文献[36]。不难把定义推广到A和B为非方阵的情形（A，B有适当维数）。

引理1.1设f，g:{0，1}n→{0，1}n是两个合取布尔网络的布尔函数，A，B分别为其邻接矩阵，则f∘g的邻接矩阵为A⊗B。

引理1.2若A是f的邻接矩阵，则A（k）是fk的邻接矩阵。

证明见文献[36]。

例1.2考虑例1.1中网络，其邻接矩阵计算，且有：

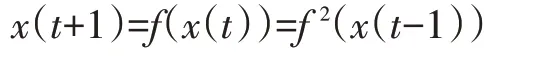
即：

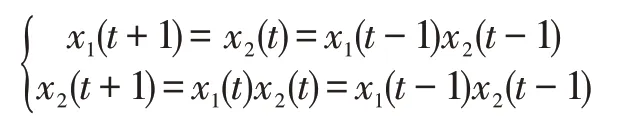
可以看出A（2）为f2的邻接矩阵。

设网络（1）的邻接矩阵为A，fk就表示状态x（t）和状态x（t−k）之间的依赖关系，由引理1.2.知，fk的变化体现到A（k）的变化上，这样就把状态变量随时间变化的依赖关系转移到邻接矩阵的变化上了。

2 新运算与关键矩阵

2.1 定义运算

为了将布尔网络代数化，需要建立网络的邻接矩阵和状态变量之间的联系，为此定义邻接矩阵和状态变量之间的运算“*”。

定义2.1设A为一合取布尔网络的邻接矩阵，状态变量x=（x1，x2，…，xn）T，记Ii={j|aij=1}，定义：

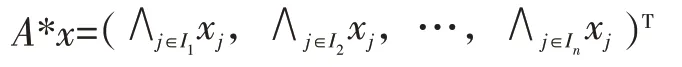
为A作用于x的状态变量，记A*x的第i个分量为（A*x）i，其中i=1，…，n。

注：A*x=（∧j∈I1xj,∧j∈I2xj,…,∧j∈Inxj）T直接取决于集合Ii={j|aij=1}，不妨称A*x与（I1，I2，…，In）T对应。对于输出函数的邻接矩阵和状态变量之间同样可定义“*”。根据以上定义，合取布尔网络的表示就可以简化，看一个例子。

例2.1上例1.2中网络可如下等阶：

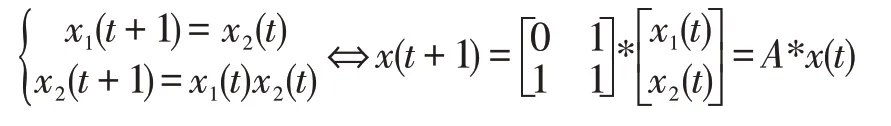
对形如（1）的合取布尔网络，若用A表示邻接矩阵，B表示输出函数的邻接矩阵，采用上述定义的矩阵和向量之间的运算，则：

（1）⇔x(t+1)=A*x(t),

（2）⇔y(t)=B*x(t).

2.2 运算性质

引理2.1设A为合取布尔网络的邻接矩阵，B为输出函数的邻接矩阵，x=（x1，x2，…，xn）T为状态变量，则（B⊗A）*x=B*（A*x）。

证 明：（B⊗A）ij=max{bi1a1j，bi2a2j，…，binanj}，设A*x与（I1，I2，…，In）T对应，B*x与（J1，J2，…，Im）T对应，B*（A*x）与（Z1，Z2，…，Zm）T对应，（B⊗A）*x与（K1，K2，…，Km）T对应，则要证Zi=Ki，i=1，2，…，m。由定义2.1知：

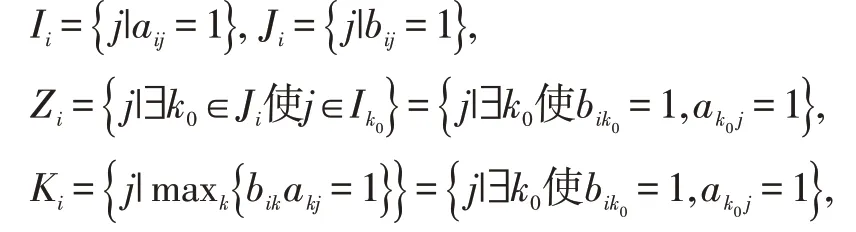
容易看出Zi=Ki，i=1，2，…，m，得证。

进而知：

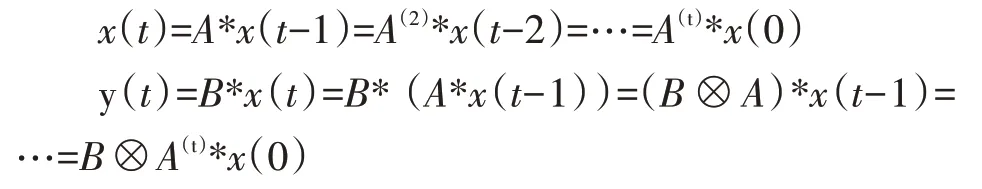
其中不难验证B⊗A⊗A=B⊗A（2）。

可见，网络在t时的输出由B⊗A（t）和初始状态决定，由于初始状态的任意性，矩阵B⊗A（t）就显得尤为重要。

2.3 关键矩阵

定义2.2称为合取布尔网络在[0，N]上的关键矩阵。

记li={j|Lij=1}，由“*”的 定 义 易 知

其中i=1，…，（N+1）m。

这提示我们合取布尔网络的输出序列完全由其初始状态和邻接矩阵以及输出函数的邻接矩阵决定，于是有：

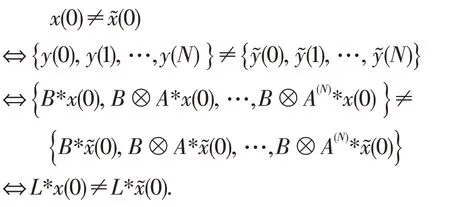
记C为只含一个元素的li的并集，于是C⊆{1，2，…，n}。

2.4 主要结果

定理2.1合取布尔网络（1），（2）在[0，N]上能观的充要条件是C={1，2，…，n}。

证明：充分性

若C={1，2，…，n}，则∃i1,i2,…,in使lik={jk}，∀k=1，2，…，n，且 有{j1，j2，…，jn}={1，2，…，n}，故 有(L*x)ik=xjk，于是若初始状态的分量xjk(0)≠xjk(0)就一定 有从 而 有 若x(0)≠x(0)，就一定有，网络在[0，N]上能观。

必要性

用反证法，即证若C≠{1，2，…，n}，推出网络不能观。定义C0={j|∃i∈{1，2，…，（N+1）m}且|li|>1;j∈li}，有C∪C0={1，2，…，n}。因 为C≠{1，2，…，n}。于是∃j0∈{1 ,2,…,n}，j0∉C。

（1）若j0∉C0，则∀i∈{1，2，…，（N+1）m}，j0∉li。若令

（2）若j0∈C0，不妨设j0∈li，若令

注：由定理知判断网络在[0，N]上的能观性只需计算[0，N]上的关键矩阵L，矩阵L的阶数是（N+1）m×n。

例2.2考虑以下合取布尔网络

其中：

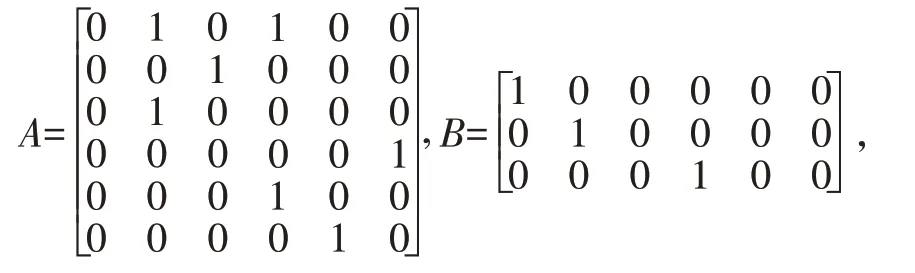
计算该网络在[0，2]上的关键矩阵

观察L可以发现l1={1}，l2={2}，l3={4}，l5={3}，l6={6}，l9={5}，故C={1，2，3，4，5，6}，因此网络在[0，2]上能观。

3 具有强连通图的合取布尔网络的能观性

定义3.1若∃N>0，使得布尔网络在[0，N]上能观，则称该网络能观。

布尔函数f的依赖图是一个有向图，它有n个对应于f的n个变量x1，x2，…，xn的顶点，如果fj依赖xi就有一条由顶点i指向顶点j的有向边，记为i→j。如果对有向图的任意两个顶点i，j都存在互通的边，则称有向图是强连通的。强连通图的循环数是它简单（最短）定向循环（顶点不重复）长度的最大公约数。

引理3.1考虑一合取布尔网络，A为邻接矩阵，假设网络具有强连通图，l为循环数，则∃k0使A（k）=A（k+l）对任意k≥k0成立。

证明参见文献[36]。

由上述引理知对具有强连通图的合取布尔网络来说其邻接矩阵A的幂次在足够大时（设大于等于k0），A（k）按周期为l的规律出现重复（k≥k0），也即是当N充分大时[0，N]上的关键矩阵L后面的行出现重复。由定理2.1知判断网络在[0，N]上的能观性时L中重复出现的行没有作用，于是我们考虑删去L中重复出现的行。

定理3.1在引理3.1的条件下，网络的能观性等价于网络在[0，k0+l−1]上的能观性。

证明.设B为输出函数的邻接矩阵，由引理3.1知当网络满足引理条件时，有

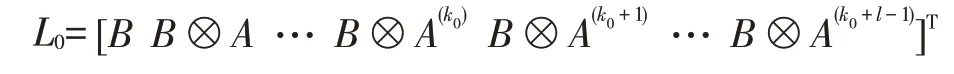
为[0，k0+l−1]上的关键矩阵。由定理2.1知判断有强连通图的合取布尔网络的能观性就等价于判断网络在[0，k0+l−1]上的能观性，得证。

例3.1考虑以下布尔网络的能观性

该网络有强连通图且其循环数为2（参考文献[36]）。设输出函数y（t）=y1（t）=x1（t），有

4 结语

本文研究了一类特殊的布尔网络——合取布尔网络的能观性。由主要结果定理2.1可见，判断合取布尔网络在[0，N]上的能观性所用到的矩阵阶数为（N+1）m×n，对于具有强连通图的合取布尔网络判断能观性最多计算的矩阵阶数为（k0+l）m×n。