和声算法在含DG配电网故障定位中的应用

2021-09-23苏鑫

电子技术与软件工程 2021年12期

苏鑫

（华北水利水电大学河南省郑州市 450000）

与以往的优化算法对比，和声算法具备操作起来简单，且容易实现的优点。在含分布式电源配电网的故障定位中有效应用本文所述的算法，从而有效建立，可以应用在不同分布式，电源投切的开关函数，并融合区域划分的方式，有效减少可行解的维数，从根本上提高故障定位的速度。

1 和声算法的概述

和声算法(HarmonySearch, HS)来源于Improvisation by musicians之中，通过深入的研究及探索，有效取得了范围之内能够达到最好的解，或仅次于范围之内能够达到最好的解。本文所述的技术方法，可对存在的问题进行完善和改进，同时对参数设置进行严格把控，然后根据具体现状的改变，有效放置与该记忆库中，之后在HM中进行搜寻和查找。最后有效评估搜索后的新解及HM的最差解，如果新解比HM的最差解理想，就可进行更换，但是若没有太大变化，就保持现状。通过这样的方式多次进行，能有效满足最后的条件即可停止。

2 具体运用

2.1 编码方式

在配电网中，如果将FTU监测系统装置在不同的开关上，并且线路有故障问题出现，但是FTU保持正常工作的状态，就可对故障电压及故障发生的具体时间进行采集，并及时将开关的状态信息进行上传。配电网中包括两种电流、运动物体等所经过的路线，其一为正常的，其二为存在故障的，对于此种问题的存在，二进制编码最为适用，继而对线路的情况进行表示，正常情况下Lt取0，故障情况下Lt取1。

2.2 开关函数

开关函数主要运用于对开关及线路状态函数的转换，其将开关与线路之间的关系进行了良好的反映。在单电源供电的配电网络中，较为适用，而对于包含DG的配电网络，对于开关函数的运用是非常不适合的。此外，DG的投切，会直接影响网络拓扑的改变，因此开关函数也应进行有效的改变。针对于以上存在的现象，此文构造了适合运用，于不同分布式电源投切的开关函数：

在此公式中，I*J（S）是开关J所希望的开关函数，其值不是0就是1，基本不存在第三种情况。逻辑或者运算为∏。下游路线J中，存在故障问题d的数值范围就是SJd；而N1可将其有效的结合在一起。G是DG主要的连接纽带，如果有DG接入的时候数值可取去，如果没有接入就为0。上游路线J中，存在故障问题u的数值范围就是SJu。而N2可将其有效的结合在一起。而∏所代表的就是逻辑以及运算。

在公式中，如果将g的取值设为0的时候，就不存在分布式电源接入的配电网，这个时候适合运用在单电源供电网络。如果有分布式的电源接入到电网中，将g的取值设为1的时候，这个时候的开关函数为I*J（S）=∏SJd-∏SJu，适合运用在含DG的系统内。因此，该公式的应用范围非常大，一方面可将其应用在单电源的系统里，另一方面还可应用在分布存在差异的开关函数中。

图1

图2

表1：GAHS及HS对电网单故障仿真统计表

表2：GAHS及HS对电网单故障仿真统计表

2.3 适应度函数

适应度函数具备构造合理性至关重要，会直接影响到所存在问题的最优解。所运用的适应度函数不一样，其结果也有所不同。可以说适应度函数构造越科学有效，那么所算出的最优解与实际越接近，对于故障定位的准确性也越高。对于配电网故障的定位问题，提出了以下适应度函数：

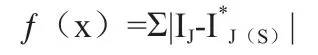
公式中：在第个开关的地方，FTU存在的故障问题的主要显示就是IJ，而良好的期望状态就是I*J（S），此被称之为开关函数。N所代表的的开关的总数量。其实该公式中有一定的问题存在，在配电网出现故障的时候，故障点到达电源线路都极有可能发生漏盘或者误判的情况。

3 具体仿真实例研究

想要从根本上验算并证实算法的具体性质和功能，按照实际实践情况的差异，对存在的异常问题进行了具体仿真实例研究。本文以图1的五个较为繁杂的模型为例，进行了具体仿真实例研究，并根据实际的规划手段，有效降低其工作的复杂程度。

未对DG状态进行连接的过程中，其正面的方向，所指向的是最为关键电源的承载的重量。若将其连接，电源S的下级开关包含S1、2、3、9、10等；若上级的电源是DG1，其开关包含S11......S18，若上级的电源是DG2，其所包含的是S22、28、29、30；若上级的电源是DG3，其主要包含S25、26、27；若上级的电源是DG4，其所包含的开关为S19、20、21、23、24；若上级的电源是DG5，主要包含S4......S8。

3.1 比较完善前后该算法的性质和功能

将K1单故障、K1及K2双重故障作为实例进行研究，对两种方式进行应用。

进而对单故障K1，以及双故障K1及K2，持续让其运行，次数为一百次，从而分别进行求解，从根本上高效寻找故障设备有故障部件多次进行的次数，以及消耗时间，并计算出平均迭代次数及具体消耗时间。平均迭代次数及消耗时间的求解方式为，在任何工作完成运行以后，在求出最为理想的计算结果后，并相关信息进行全面有效的记录，之后对100次的记录结果进行平均求值，从根本上高效寻找故障设备有故障部件多次进行的次数。研究发现，GAHS及HS两种算法，具有极高的准确率，可达9成以上，具体数据如表1、表2所示。

通过表1及表2可了解到，GAHS中位数的重复反馈次数比HS要少，同时GAHS消耗时间的中位数比HS耗时间的中位值显著要短，证明GAHS与HS较，其能更快的对最优解进行收敛，证明GAHS的搜索率更为理想。

3.2 信息畸变现状下具体仿真实例研究

在现实中，开关FTU主要在室外进行安装和装置，由于环境条件的不确定性，会对通信造成一定的威胁，进而氧化了开关接触点的表面，配电网柱上的FTU开关通常都会在户外装设，因为受到周围环境，以及天气及通信的影响，导致辅助开关触点的表面被氧化，进而使得FTU上传的信息出现畸变。对配电网故障定位可靠性及准确性造成了非常严重的影响，所以此算法一定要具备极大的故障容许度。想要深入研究和分析该算法故障的容许度，将路线三所出现的K1故障作为研究实例，进而具体研究其现存的信息数据，以及重位信息畸形变化的情况。

和声算法评价函数的寻优过程如图2所示。

在经有效和声操作后，适应度的最小值为2.5。这个时候相应的最优解编码为1的线路编号仍旧是3，所以故障线路就是3，与之前设定的情况符合，所以和声算法的定位具备极高的准确性。

由此可知，运用和声算法对故障的地位进行定位，即使是在故障过流信息发生畸变、丢失的不利条件下，和声算法依然在准确性方面有较高的水准，证明此种算法也有非常高的容错性。