输入地震动相位特性对不同类别场地土层地震反应影响

夏峰 孙楠 危凤海

摘要：以某Ⅷ度设防区基岩场地地震危险性计算为基础，拟合不同随机相位的人造地震动时程作为输入，采用一维等效线性化方法，计算了Ⅱ类、Ⅲ类和Ⅳ类典型场地的土层地表地震反应。结果表明：①在不同地震动强度、不同随机相位基岩时程输入条件下，对不同类型场地土层地震反应计算得到的地表加速度峰值和反应谱值相对极差差别较大，地震动相位特征对土层地震反应的影响不可忽略;在反应谱特征周期2.0s内，地表峰值和反应谱值变异系数随输入地震动强度的增大有增大趋势;②采用统计学方法计算给出了不同场地类别的基岩输入随机相位样本时程的必要数量，不同场地类别不同地震强度输入条件下所需要的最少样本量不同。在输入地震动强度不大（PGA<0.20g）且满足反应谱变异系数在均值加1倍标准差范围内时，不同类别场地至少需要15组不同随机相位的基岩时程，基本能满足均值统计要求;在输入地震动强度较大（PGA≥0.20g），满足反应谱变异系数在均值加1倍标准差范围内时，至少需要30组不同随机相位的基岩时程，才能满足均值统计要求。

关键词：相位特性;场地类别;地震动时程;土层地震反应;样本容量

中图分类号：P315.914文献标识码：A文章编号：1000-0666（2021）04-0656-09

0引言

土层地震反应是重大项目工程场地地震安全性评价技术的关键环节，同样也是编制《中国地震动参数区划图》（GB18306—2015）（以下简称2015版地震动区划图）时双参数调整的技术关键之一。在重大工程抗震设计分析中，需要利用地震动时程作为地震输入来进行结构地震反应分析计算，考虑到强震记录数量有限，工程上通常是以人工合成地震动作为各种地震反应分析的输入。通常采用概率危险性分析计算得到的基岩反应谱或结合相关规范给定设计反应谱拟合获得的地震动时程，称为人造地震动，以此作为土层反应计算或结构抗震验算的地震动输入。地震动时程的基本要素包括峰值、频谱特性和持续时间等（胡聿贤，2006），其中频谱特性可由幅值谱和相位谱特性表述。在地震动合成过程中，一般只对地震动这3个基本要素加以约束，对于相位特征要素一般采用（0～2π）区间内均匀分布的随机量（胡聿贤，何训，1986），故人造地震动相位特性存在一定的不确定性。因此，在进行具体土层地震反应分析或结构抗震验算时，基岩时程相位特性具有一定的随机性和不确定性。

前人的研究表明，地震动时程相位特性是地震动时程的重要特性之一。Ohsaki（2010）首次对地震动相位特征进行研究，发现地震动相位与幅值谱是同样重要的，相位谱中包含了许多重要信息，还进一步研究了相位对时程的影响，提出了相位差的概念;金星和廖振鹏（1993）对地震动相位特征进行了专门研究，从理论上给出了地震动的相位谱和相位差谱的定量关系，并明确了相位谱与相位谱主值的本质区别，说明了地震动的相位信息是构成地震动强度和频率非平稳特征的主要因素;石树中和宋初新（2004）对相位谱与地震动参数关系进行分析，结果表明在幅值谱和强度包线函数相同的情况下，相位谱对峰值和反应谱具有较大的影响;程纬等（1999）也对地震动相位谱与相位差谱分布特征进行了研究，发现低频地震动具有非平稳特性要强于高频的情况。

以上研究侧重对地震动相位特性进行阐述，在工程实际应用方面涉及甚少。当前地震安全性评价规范要求，对于Ⅱ级和地震小区划工作中进行土层地震反应分析时，应给出不少于3条相互独立的随机样本基岩时程（卢寿德，胡聿贤，2006）。但以往的工程经验及计算分析表明，在土层地震反应分析工程应用中，目前较为普遍的做法是选择3条基岩加速度时程作为地震动输入，这是不够的，应适当地增加时程数量（蒋维强，2009）。另外，李亚军（2016）以上海某实际工程场地为例，从统计学角度得出土层地震反应所需不同随机相位基岩时程的样本容量，但仍未具有一定的代表性。以上工程应用方面的探索具有一定工程意义，但对于不同类型的场地和较强地震动输入条件下的影响程度，还需做出进一步研究分析。

本文以3个重大工程安全性评价的不同类型场地（Ⅱ类、Ⅲ类和Ⅳ类）为例，采用某Ⅷ度设防区的4个超越概率水准（50年超越概率分别为63%、10%、2%，100年超越概率为1%，以下简称50a-63%、50a-10%、50a-2%及100a-1%）拟合的不同相位时程为输入，使用常用的一维等效线性化方法进行土层地震反应，分析随机相位特性对不同强度输入和不同场地类别条件下的土层地震反应结果的影响，并进一步采用统计学方法计算给出不同强度输入和不同场地类别条件下土层地震反应所需不同随机相位基岩时程的样本数量。

1场地地震反应分析建模参数

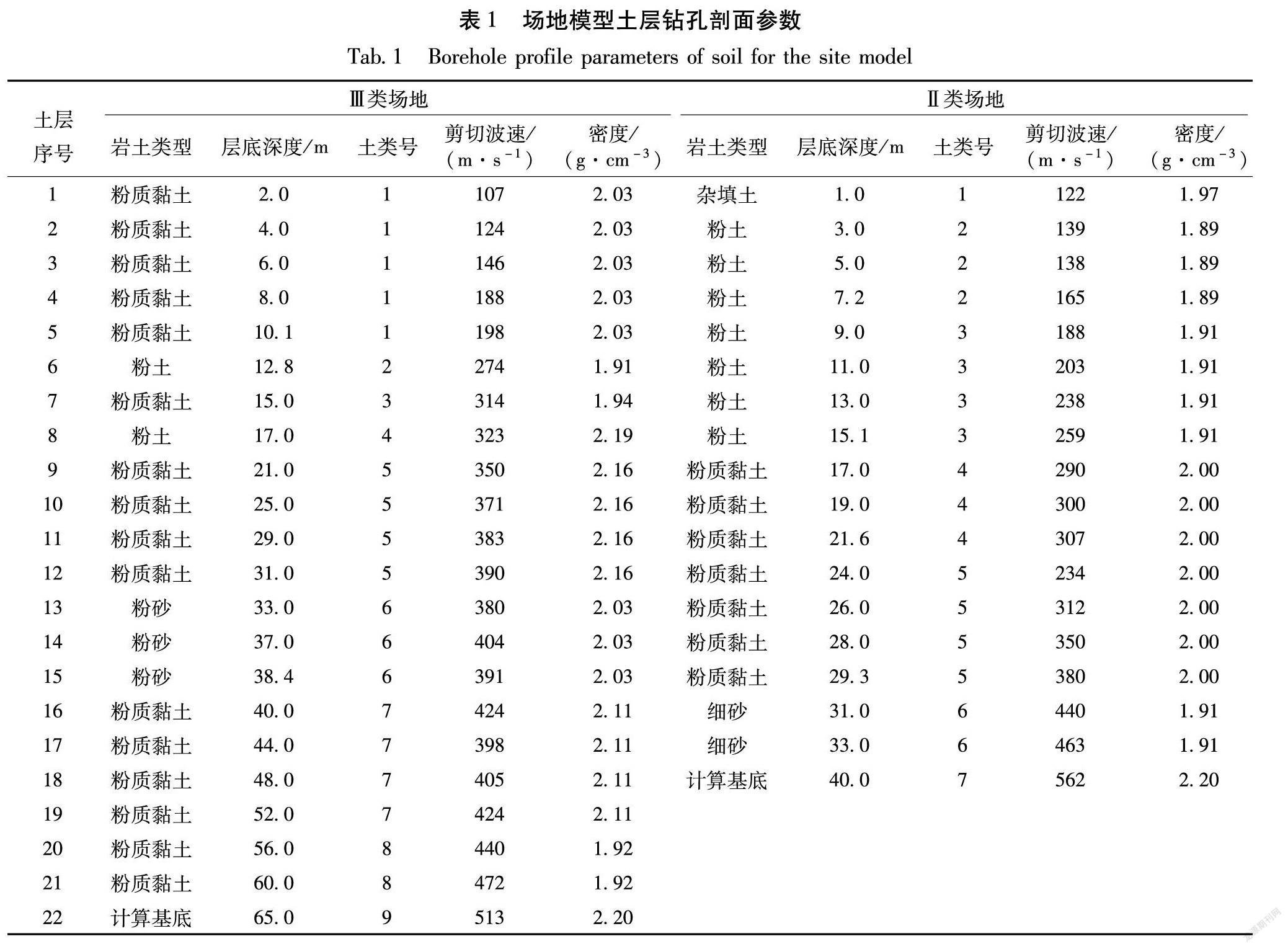
本文分别选用Ⅱ类、Ⅲ类和Ⅳ类典型场地各一个，其中Ⅳ类场地的土层反应建模参数参见夏峰等（2016）的研究，用于计算的Ⅱ类、Ⅲ类场地土层反应建模参数见表1、2，这些参数均由重大项目工程场地安评工作实测所获得。

2输入基岩地震动确定

本文采用《中国地震动参数区划图》（GB18306—2015）地震统计区、潜源参数和地震动衰减关系，对某Ⅷ度设防区场地进行了地震危险性概率分析计算。考虑到2015版地震动区划图给出了极罕遇地震动参数，故本文分别计算了场地100年超越概率为1%和50年超越概率分别为2%、10%、63%的基岩5%阻尼比的结果，分别对应的场地设防水准是极罕遇地震动、罕遇地震动、基本地震动和多遇地震动水平，如图1所示，其对应的基岩加速度峰值分别为554.8、369.2、186.1和48.2Gal。

基岩加速度主要由加速度峰值、频谱和振动持续时间这3个要素决定（胡聿賢，2006）。将由地震危险性分析得到的基岩峰值加速度和反应谱作为合成的目标函数，结合适应本场址地震活动特征的强度包络函数，采用拟合目标函数的三角级数迭加法合成基岩地震加速度时程，作为场地地震动反应分析的输入基岩的时程（胡聿贤，1999）。本文给出30个相互独立的随机样本时程，反应谱拟合周期控制点数不少于50个，且大体均匀地分布于周期的对数坐标上，控制点谱的相对误差应小于5%。在满足上述技术要求前提下，本文以50a-2%、50a-10%、50a-63%和100a-1%的基岩反应谱为目标谱各合成30个相互独立的样本时程，作为土层地震反应分析的输入，由于篇幅原因，仅列出3组时程样本（图2）。从图2可以看出，人工拟合地震动时程选取的随机数不一样，即选取的相位不一样，拟合的时程也是不一样的。例如加速度到达峰值对应的时间差别很大，且加速度的方向也不一致。不同相位地震动时程的差异性使得输入计算时得到的地表反应谱可能存在一定的差异，下文将从统计角度详细研究减小这种差异性需要的样本数。

3 土层反应分析

本文采用一维等效线性化方法，分别计算了4个超越概率水准的各30组不同随机相位的基岩地震动时程的土层地震反应（计算中基岩地震动幅值减小一半输入），得到相应的地表加速度反应谱，如图3所示。

为分析不同相位、不同强度地震动时程输入对不同场地类别地表加速度反应谱各周期点的影响，分别计算最大值、最小值、平均值、标准差、相对极差和变异系数等。

标准差是方差的算术平方根，能反映一个数据集的离散程度，可表示为：

式中：x为样本均值;n为样本个数;为第i个样本值。

相对极差即为极差的相对值，可用于表示数值的离散（集中）程度，表示为：

式中：为样本最大值;为样本最小值;x为样本均值。

变异系数是原始数据标准差与原始数据平均数的比，可表示为：

式中：σ样本标准差;样本均值。

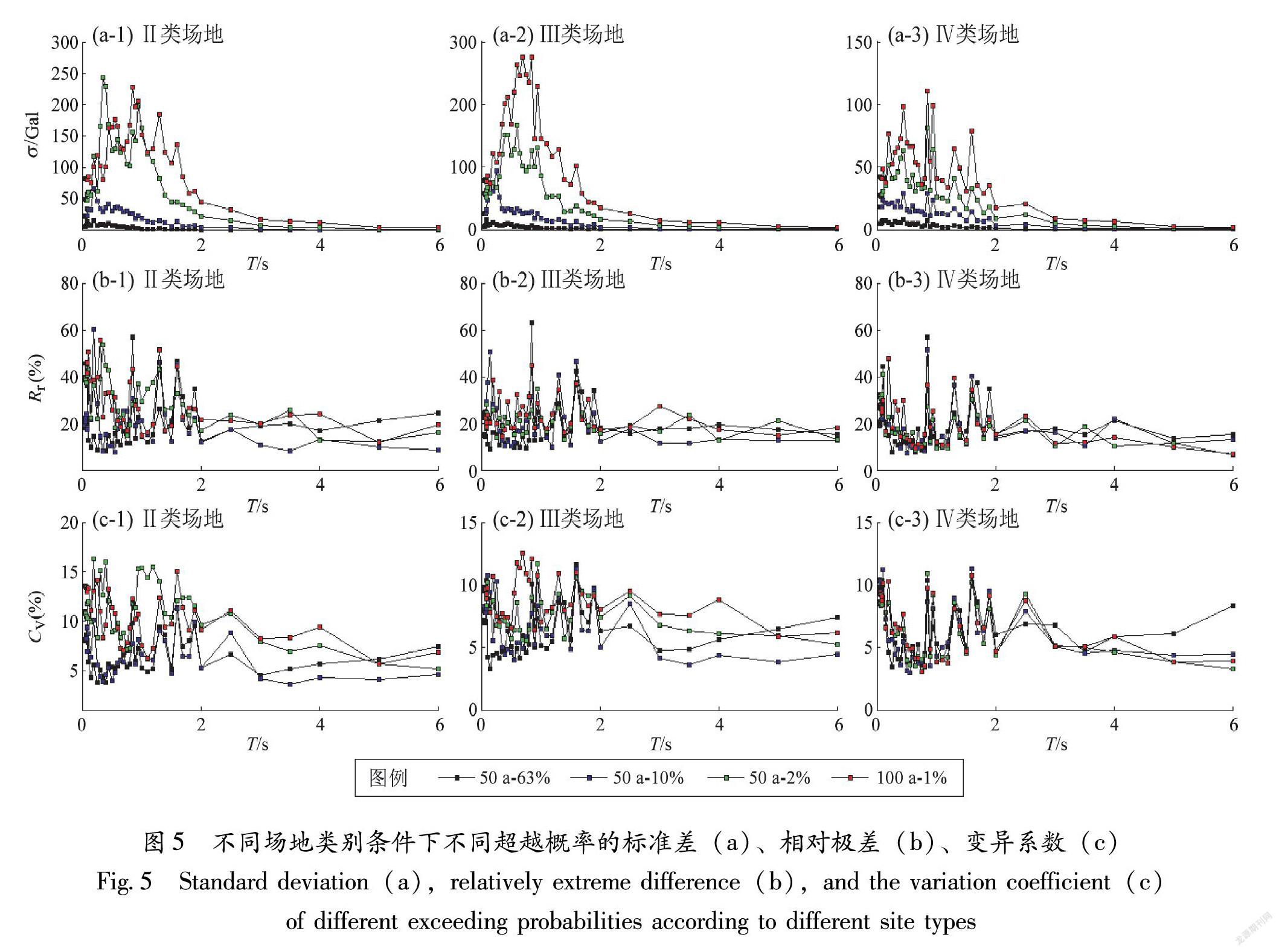
通过对在不同超越概率各30组不同随机相位地震动输入条件下的计算结果按式（1）～（3）进行整理，得到了不同场地类别条件下4个超越概率水准的地表峰值加速度和反应谱各周期点的最大值、最小值、平均值、标准差、相对极差和变异系数等相关参数，还得到了地表加速度反应谱各周期点随相位数增加的均值。由于篇幅原因，表3仅给出了30组不同随机相位输入下地表峰值加速度计算结果;图4仅给出了地表峰值加速度随不同随机相位数（3～30）增加的均值图;图5为30组不同随机相位输入下得到的在不同场地类别下不同超越概率的地表加速度反应谱各周期点的标准差、相对极差和变异系数等。

从表3可知，在不同场地类别和不同强度的地震条件输入下，不同相位的地表峰值加速度值PGA的相对极差通常在20%以上，最大接近50%，且在较强地震动输入的Ⅱ类场地条件下可能更大。故在确定地表地震动峰值加速度时应适当考虑不同相位结果之间的差异，在强地震动输入的Ⅱ类场地条件下更要特别注意。

由图4可知，当时程数目较少时，地表峰值加速度均值有一定的不稳定性，当输入较强地震动时更为明显，但当时程数量增加到一定数量后，地表加速度均值趋于稳定。结果显示，目前对于Ⅱ级地震安评，仅采用3条基岩加速度时程作为地震动输入略显不足，宜适当增加。

图5的计算结果也表明，在不同场地类别条件下和不同超越概率水平的地震输入下，标准差随着反应谱值的增大而基本呈现出增大的趋势（图5a），在50a-2%和100a-1%地震动输入条件下，在反应谱特征周期2s内标准差的震荡变化尤为剧烈（图5a）。地表各周期反应谱值Sn（T）的相对极差和变异系数差别也较大，在反应谱特征周期2s内的变化尤为剧烈（图5b、c）。总体来看，Ⅱ类场地条件下S（T）的变异系数较Ⅲ类和Ⅳ类场地条件下的大，在50a-2%和100a-1%的地震动输入条件下比50a-10%和50a-63%的地震动输入时大;3类场地条件下的变异系数绝大多数分别在13%、12%和10%以下震荡变化，但当输入地震动强度不大时，变异系数绝大多数均在10%以下震荡变化（图5c）。

4随机相位时程样本容量的确定

前文计算结果表明：随着时程数量的增加，峰值及反应谱值均值最后是趋于稳定的。不同随机相位时程计算得到的地表反应谱值Sn（T）基本呈正态分布。本文采用统计学方法来确定取得可靠均值所需随机相位样本时程的必要数量（样本容量）。

设随机变量x=Sn（T），则x～N（μ，a），则均值μ的置信度为1的置信区间为1-a，总体均值的置信区间为：

式中：Z为可靠因数：a为标准差;n为必要样本容量。

令允许误差△=Z-+，可得出：

式中：Cv为谱值变异系数;8为允许误差率。

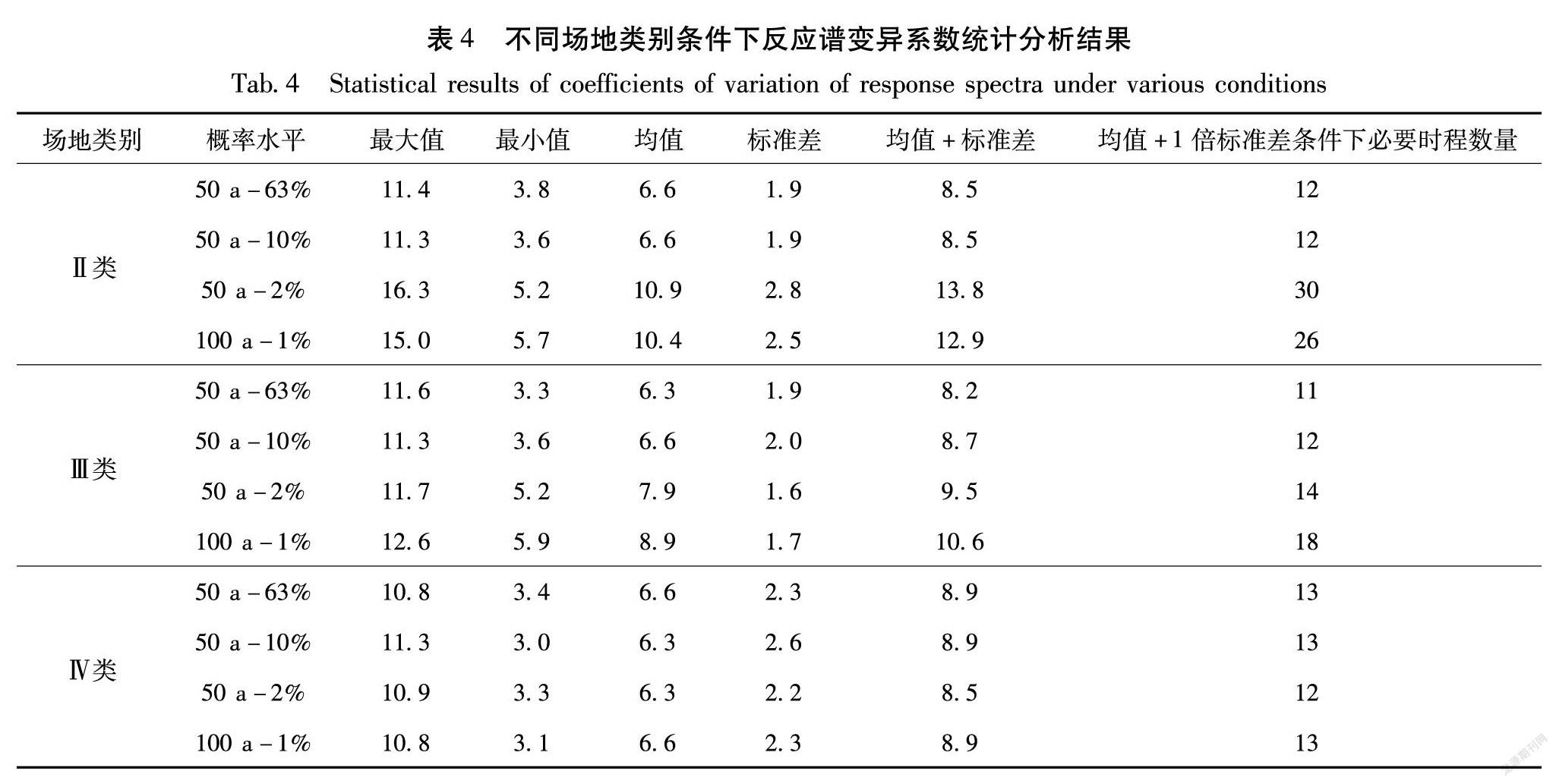
常规来说，对于95%的置信度（即α=0.05），对应的可靠因子Z值为1.96。本文计算时控制允许误差率在5%，则反应谱值（含峰值）统计方法的统计精度取决于各离散点变异系数Cv值，只有各离散点变异系数Cv值同时满足一定统计意义的期望值才能满足工程精度要求。笔者进一步统计Ⅱ类、Ⅲ类和Ⅳ类场地地表反应谱变异系数值，给出不同地震动强度输入条件下Sn（T）变异系数的最大值、最小值、均值和标准差等，并根据式（5）计算得到了满足均值加1倍标准差条件下的必要的时程数量，结果见表4。

据表4可知，在土层地震反应分析时，不同的场地类别和不同强度地震输入需要的输入时程量不一样，在输入地震动强度不大（PGA<0.20g时）且满足Sn（T）变异系数在均值加1倍标准差范围内时，不同场地类别至少需要有15组不同随机相位的基岩时程，才能基本满足地表峰值和反应谱均值的误差率在5%以内的概率为95%，即每个概率水取至少取15组不同随机相位的时程可基本满足均值统计要求。但在输入地震动强度较大（PGA≥0.20g）时，尤其是在Ⅱ类场地时，要满足Sn（T）变异系数在均值加1倍标准差范围内，至少需要30组不同随机相位的基岩时程才能满足地表峰值和反应谱均值的誤差率在5%以内的概率为95%，即每个概率水准取至少30组不同随机相位的时程可基本满足均值统计要求。

5结论

本文选取典型的Ⅱ类、Ⅲ类和Ⅳ类场地，在不同强度基岩地震动输入条件下，统计分析了不同输入地震动相位对地表反应谱的影响，主要得到以下结论：

（1）采用不同地震动强度、不同随机相位基岩时程对不同场地类型进行土层地震反应分析时，计算得到的地表加速度峰值和反应谱值相对极差较大，在Ⅱ类场地尤为明显，故地震动相位特征对土层地震反应的影响不可忽略;在反应谱特征周期2.0s内，地表峰值和反应谱值变异系数随输入地震动强度增大有增大趋势，在Ⅱ类场地尤为明显。

（2）场地地震安全性评价工作中常规采用3组不同随机相位基岩地震动时程进行土层地震反应分析，时程数量明显不足，在较高烈度设防区尤为明显，宜适当增加合成时程的数量。

（3）采用統计学方法计算给出了不同场地类别的基岩输入随机相位样本时程的输入时程量。不同场地类别、不同地震强度输入条件下所需要的最少样本量也不一样。在输入地震动强度不大（PGA<0.20g）且满足反应谱变异系数在均值加1倍标准差范围内，不同类别场地至少需要15组不同随机相位的基岩时程，才能基本满足均值统计要求;在输入地震动强度较大（PGA≥0.20g）时，尤其在Ⅱ类场地，满足反应谱变异系数在均值加1倍标准差范围内，至少需要30组不同随机相位的基岩时程，才能满足均值统计要求。

（4）由于本文选取的各类场地代表性有限，且基岩输入强度跨度过大，未做更细致计算分析，所得结论可能有一定的局限性。

参考文献：

程纬，刘光栋，易伟建，等。1999。地震动相位谱与相位差谱分布特征的研究[J].湖南大学报（自然科学版），26（2）：82-85。

胡聿贤，何训。1986。考虑相位谱的人造地震动反应谱拟合[J].地震工程与工程振动，6（2）：37-51。

胡聿贤。1999。地震安全性评价技术教程[M].北京：地震出版社

胡聿贤。2006。地震工程学[M].北京：地震出版社

蒋维强。2009。土层地震反应分析的地面加速度峰值计算研究[J]防灾减灾工程学报，25（3）：283-287。

金星，廖振鹏。1993。地震动相位特征的研究[J].地震工程与工程振动，13（1）：7-13。

李亚军。2016。基岩地震动相位特性对土层地震反应影响分析[J]世界地震工程，32（1）：124-129。

卢寿德，胡聿贤。2006。工程场地地震安全性评价宣贯教材[M].北京：中国标准出版社，103。

石树中，宋初新。2004。相位谱与地震动参数关系的分析[J].浙江工程学院学报21（增刊1）：19-22。

夏峰，郭宝震，余大新，等。2016。厚层淤泥质粉质黏土的动力特性参数对地表地震动参数的影响[J].地震工程学报，38（3）：391-397.

Ohsaki Y.2010. On the signifieance of phase content in earthquake ground motions[].EarthqEng Struct Dyn， 7（5）： 427-439

GB183062015，中国地震动参数区划图[S]

Influence of Phase Properties of the Input Ground Motion on the Earthquake Response of Different On-site Soil

XIA Feng SUN Nan， WEI Fenghai

（I. First Crust Monitoring and Application Center， China Earthquake Administration， Tianjin 300180， China）

（2. State Grid Tianjin Constrnction Company， Tianjin 300143， China

（3. China Railway Beijing Group Co. ， Lid.Beiing 100860）

Abstract

On the basis of the seismic hazard calculation of some bedrock site in Intensity 8 earthquake fortification zone and using one-dimensional equivalent linearization method， we input the fitted time history of artificial ground motion with different random phases， and calculated the ground response spectrum of Site Class and N The following conclusions are reached：（1） the earthquake responses of different types of sites are carried out by using bedrock time histories with different seismic intensities and random phases. The difference of relative extrema of the peak ground acceleration values and the response spectrum values calculated is significant. The influence of phase characteristics of the time history of ground motion on the soil earthquake response is innegligible. Within 2.0 s of the characteristic period of the response spectrum， the variation of the ground motion values and the response spectrum values increases with the increase of intensity of input ground motion.（2 the necessary quantity of the time histories with random phases on different sites is calculated by the statistical method. The minimum sample size depends on the following conditions： when the input ground motion is small （PGA<0.20g） ， and the variation coefficient of response spectrum is within the range of mean value plus one-fold standard deviation， at least 15 pairs of time histories are needed to meet the average statistics. When the input ground motion is large （PGA>0.20 g） ， and the variation coefficient of response spectrum is within the range of mean value plus one-fold stand-ard deviation 30 pairs of time histories are needed to meet the average statistics.

Keywords： phase properties; site class; ground motion time history; soil earthquake response; sample size