利用混合概率预测模型分析华北地区地震活动特征

马永 毕金孟 宋程 尚先旗

摘要：在可操作的地震预测研究过程中，构建效能可评价、符合区域地震活动特点的预测模型是至关重要的。以地震活动频发、地质结构复杂的华北地区为研究对象，选择相对强度模型、力矩比模型和简单平滑模型等3种地震概率预测模型，利用1970—2019年华北地区3.0级以上地震数据，以10a为异常学习时段，以1a为步长，分别开展1a、3a和5a尺度下5.0级以上地震的回溯性滑动预测研究。通过Molchan图表法和T-test检验方法，对预测模型进行效能评估，优化了模型参数，确定了3种预测模型的最佳计算参数，构建了适合华北地区地震活动特点的不同时间尺度混合概率预测模型，并使用近10a的地震分析了华北地区当前的地震活动特征。       关键词：地震概率预测模型;效能评价;地震活动特征;华北地区

中图分类号：P315.7文献标识码：A文章编号：1000-0666（2021）04-0572-11

0引言

华北地区作为中国七大地理分区之一，经济发展、文化繁荣、人口稠密，同时也是构造活动强烈、地震活动频繁、地质灾害较为严重的地区之一。自有地震记录以来，整个华北地区除鄂尔多斯板块以外基本都有中强地震发生，对人民的生命财产安全造成了极大的损害。特别是1966年邢台M7.2强震、1976年唐山M7.8强震将华北地区的地震活动推到高潮。鉴于华北地区地质灾害的复杂性和地震活动的多样性，使用现有海量的地震数据开展区域地震活动特征研究，对当前震情跟踪和中强地震长期危险性分析具有非常现实的意义。

在全球的“地震可预测性合作研究”（CSEP）计划中，地震学家使用研究区域统一的地震目录和严格的地震统计检验方法，对多种地震预测模型开展“竞赛”式的回溯性预测检验，筛选出“优胜”模型并进行前瞻性的预测，为可操作的地震预测（OEF）提供了坚实的理论基础，为构建更具减灾实效的OEF系统模型提供了可能性（Jordan et al ，2011，2014）。毕金孟和蒋长胜（2019）采用传染型余震序列（ETAS）模型和Reseanberg-Jones （R-J）模型，对华北地区16次4.5级以上地震的序列参数进行拟合，得到稳定的地震序列参数。马干等（2009）根据华北地区2700多年的地震数据建立了地震活动性模型，并使用frankel（1995）提出的地震空间高斯平滑处理分析方法，获得了华北地区主要城市的地震动参数，为区域抗震设防提供了重要的基础数据。

随着CSEP计划的不断发展和完善，地震学家开发出了大量的不同时间尺度、不同计算方法的地震预测模型。在当前国际地震可预测性研究中，为消除单一地震预测模型在地震预测中的局限性，人们试图采用“扬长避短”的方式将不同的单一地震预测模型进行融合，形成混合概率预测模型，并进行预测效能检验。rhoades和Ger-stenberger（2009）将中长期尺度的EePas预测模型和PPE模型融合到STEP模型中，根据不同的融合方式形成5种混合模型，分别对5.0级以上地震进行了回溯性预测，结果表明所有的混合模型均优于单一模型。Marzocchi和Jordan （2014）将ETAS模型、ETES模型和STEP模型等按不同的权重组合，构建了意大利地区地震预测的OEF技术系统。美国“加州地震概率工作组”于2014年发展了统一的加州地震破裂预测模型（Field et al ，2014），将长期预测模型WG-CEP-UCERF 2与短期预测模型ETAS进行融合，解决了由于时间尺度的不同造成的对地震发生率预测的不一致问题。类似这种的混合模型在提高地震预测能力的同时，已逐渐成为OEF系统建设的主要选择。为此，本文引入混合概率预测模型（以下简称“混合模型”）研究方法，使用1970—2019年华北地区3.0级以上地震数据，构建适合华北地区活动特点的混合模型，分析该地区的地震活动特征，为该地区中强震的地震危险性判定、震情跟踪以及可操作的地震预测模型构建等提供模型基础和科学参考。

1构选背景及数据选取

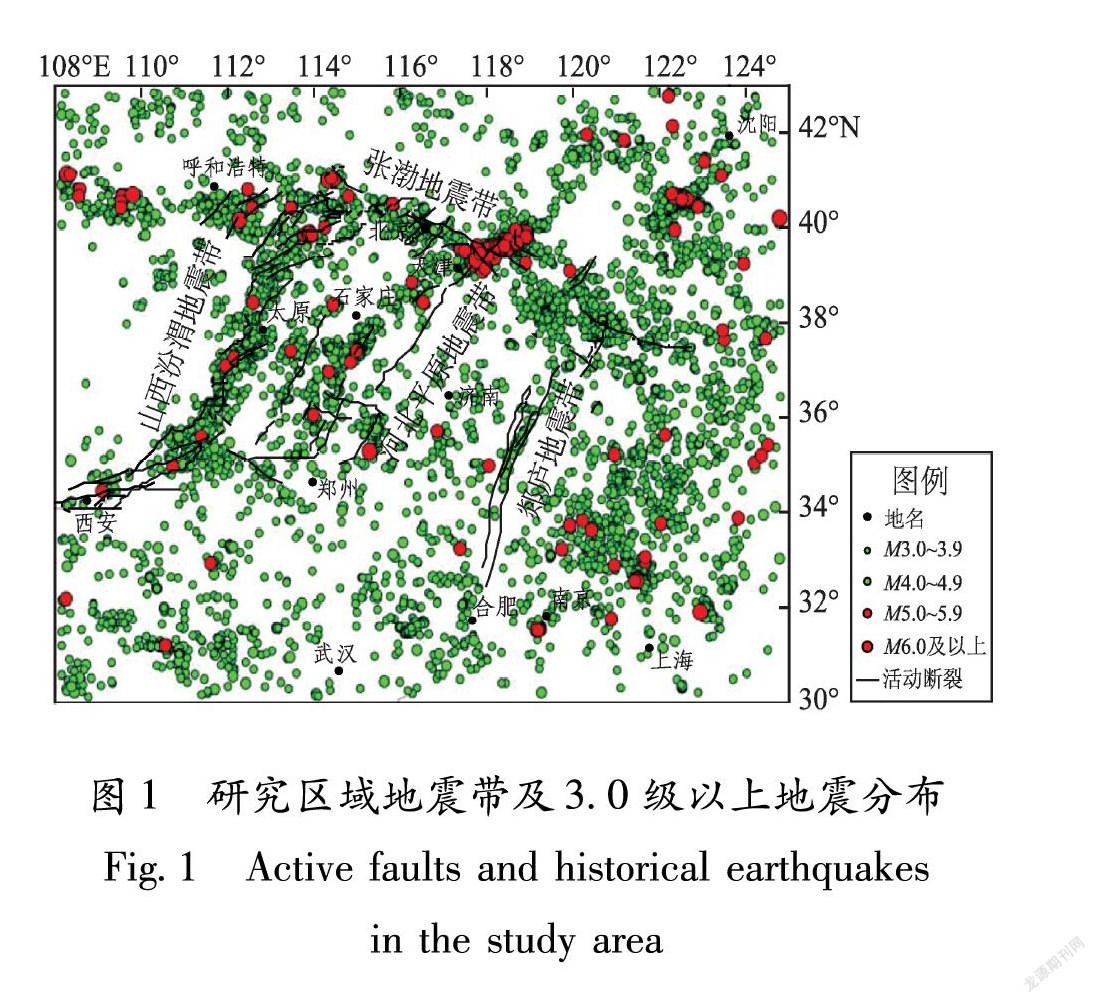
本文以华北地区（30°～43°N，108°～125°E）为研究对象，该区域在印度板块和太平洋板块的共同挤压作用下，块体活动强烈、断裂和褶皱发育、地震活动频繁（李三忠等，2011）。在地质构造上，华北地区共展布有4条主要地震带，分别是由山西地堑和渭河地堑地震活动组成的贯穿整个山西省的汾渭地震带、横跨燕山隆起和华北盆地直至渤海的张渤地震带、斜穿河北平原并与张渤地震带相交的河北平原地震带和最东侧NNE走向的郯庐地震带（图1）。

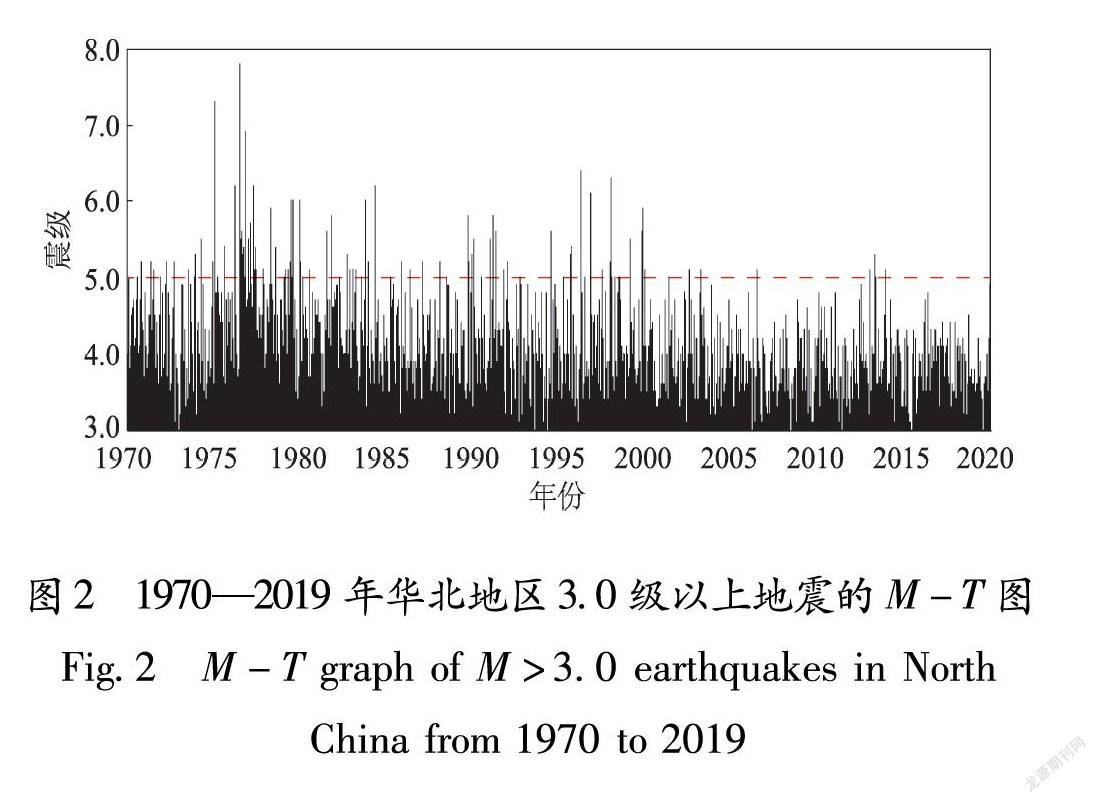
华北地区幅员辽阔，地震监测能力不尽相同，监测水平总体达到M1>2.0，在东部沿海地区达到M1=2.0，在部分地震重点监视防御区和人口密集的主要城市达到了M1=1.5（刘瑞丰等，2007，2008）。笔者使用了中国地震台网中心提供的《全国统一正式编目》地震目录，遵照文中所用地震预测模型对地震序列信息的要求，从中挑选出了1970—2019年发生在研究区内的8700次3.0级以上地震数据，其中5.0级以上地震203个，最大地震为1976年河北唐山的M7.8地震。从图1可以发现，本文所用的地震数据几乎覆盖了除鄂尔多斯板块以外的所有地区，而且在山西汾渭地震带、河北平原地震带和张渤地震带上分布更为集中。受唐山M7.8地震的影响，研究区5.0级以上中强地震大多集中发生在唐山及其周边地区，其余陆地上的中强地震均沿着活动断裂带聚集，满足历史地震活动重复发生的规律。图2为所用研究数据的M-T图，其中3.0级以上地震覆盖整个研究时段，5.0级以上中强地震主要集中在发生1976年，其它年份发生中强地震的次數相对较少，每年基本为1～5次，但2004—2019年，除2006年和2013年在研究区域分别有1次和5次5.0级以上地震外，其他年份均无5.0级以上中强地震发生。

2研究方法

混合概率预测模型是指采用多种单一地震预测模型，这些模型的计算方法各不相同，从中筛选出预测效能最优的几种模型，按照一定的权重系数将其进行混合，经过优化设计后得到具有地区针对性的混合模型。利用混合模型研究区域地震活动特征，无论在确定性预测研究方面，还是在概率性预测领域都得到了广泛的应用，已成为地震活动性研究的一种重要方法（毕金孟，蒋长胜，2017）。本文利用相对强度（RI）模型、力矩比（MR）模型和简单平滑（Triple -S）模型等3种单一地震预测模型，逐一对1970-2019年华北地区的3.0级以上地震，以10a为异常学习时段，以1a为分析步长，对5.0级以上地震分别开展1a、3a和5a尺度的回溯性滑动预测，并采用国际通用的Molchan图表法、T-test等具有针对性的统计检验方法，评估每个模型的预测效能。为每种单一模型分配不同的权重因子，构建适合华北地区活动特点的中强地震混合模型，并使用近10a的地震数据评估当下华北地区的地震活动特征。

2.1单一地震预测模型方法

RI模型是一种基于以往地震活动性来定性预测未来地震发生可能性的预测方法。该方法无需过多的定量计算和数据验证，具有参数设置少、预测效果好、且仅用点源信息便可进行地震预测和危险性分析的优点，在世界各国的地震预测中应用广泛（Nanjo ，2010，2011）。Tiampo等（2002）应用RI算法在美国南加州地区进行“回溯”和“向前”预测研究，结果表明RI模型对于不同的时间尺度和不同的震级预测范围均具有潜在的预测效能。其基本思路是首先把研究区域划分为微型网格，每个网格长度为△x;其次统计在第i个网格，学习时间段（to-t1）内震级M≥M的地震数目，其中第i个网格每天的平均地震数目用n（t，t1）表示;然后将地震数目的相对值作为RI的评分，具体RI评分表达式为n（to，t1）/nMAX，其中nMAX为n1（to，t1）中的最大值，取值范围为0～1。数值越大的地区未来发生大地震的可能性就越高，反之，发生大震的可能性就越小。应用RI模型算法预测的大地震一般发生在地震活动性相对较高的地区。

MR模型使用地震间隔时间的力矩比作为前兆预警指标，基于地震活动率与地震发生前背景地震活动性的长期异常变化关系开展地震预测。Talbi等（2013）利用日本气象厅679—2012年的全日本地震综合目录数据，证明了MR模型对未来各阶段均有较高的地震预测效能，特别是对于7.0级以上地震的预测能力明显高于其他方法。具体步骤是通过每个位置点x和采样网格尺寸r进行计算得到：

式中：和a分别是时间序列{的算术平均值和方差。为了确保用MR模型估计的最小精度和不同网格尺寸r结果的稳定性，需设置一个最小样本量n，计算过程中要求存在至少n个事件时计算出MR值。计算时在n，取值确定的前提下，网格r取值的大小直接影响MR模型的预测性能。

Triple -S模型是一种基于中强地震更容易发生在以往地震活动频率较高的地方假设的地震预测方法，其突出优点在于较少的参数设置和假设条件，不需要依据地震构造特征来划分潜在震源区，该方法利用了不同平滑函数，在世界各地得到充分应用（Zechar，Jordan ，2010）。在计算过程中需将研究空间进行精细网格化，将发生地震的位置（xeqk，yeqk）在空间范围[x1-x2，y1-y2]内地震发生率的影响表示为：

然后，采用平滑函数对r进行平滑和归一，并直接将其作为“平滑距离”，式中的K为kn（x，y）=，σ为用于平滑的参考距离。2π0

2.2模型预测效能评价方法

Molchan图表法（Molchan，1997，2010）是根据预测结果与观测目标地震之间的分布差异程度，预测研究区域强震的发震时间，并试图给出概率解释的一种统计检验方法。该方法不考虑预测地震或观测目标地震的数量和震级，仅通过异常时空占有率（r）和漏报率（v）2个参数来进行预测效能统计评价，因其简单客观的评价特性，目前已在国际上广泛地应用于概率预测的统计检验和效能评估（蒋长胜等，2011）。其中，r是指达到和超出预测警报阈值的时空范围与研究区域总的时空范围的比值;v则是未达到预测警报阈值的时空范围内实际发震的次数与研究区内总的实际地震数之比。概率预测最理想的预测效果是在预测成功率最大（v→0）情况下异常时空占有率最小（r→0）。预测效能的评价一般情况下有两种判别方式，一种是用1减去（r，v）曲线与横、纵坐标轴所包围面积的差，所得数值越大则预测效果越好;另一种是考察击中数（h）所对应的显著性水平（a），通过比较r-v曲线上各点与显著性水平等值线判断预测效能。显著性水平α值的计算公式为：

式中：N為实际发生地震总数;h为击中数，即在预测有震区域内实际发震的地震数。

T-test是基于t-test（Student 1s）检验，依据样本平均数与已知总体平均数的差异的显著程度来评价不同模型预测效能平均分布情况的一种检验方法。通过对比的方法可以更好地筛选出模型中的最佳预测模型，构建符合研究区域地震活动特征的优势预测模型。T-test的计算表达式为：

式中：N为研究样本的总个数;X为样本平均数;s为样本标准偏差;μ为样本总体期望值。

3模型参数优化与预测效能评价

模型参数设置是构建地震概率预测模型过程中非常关键的步骤之一，只有设定适合研究区域地震活动特征的模型参数，才能使预测模型达到最佳的预测效果。本文以研究区域内5a尺度5.0级以上地震的回溯性概率预测为例，分别对3种单一地震预测模型设置不同的模型参数，并通过统计检验方法对每一种地震预测模型中不同参数预测效能进行评价。依据效能评分，从中选择最优参数，确保每种模型在研究范围内的预测能力达到最优水平。

在RI模型的计算过程中，影响最终预测结果的模型参数主要是异常学习时段的最小完备性震级M和划分网格的长度△x。依据王鹏等（2011）、王霞等（2014）、韶丹等（2015）和谢卓娟等（2019）对华北地区近50年来的地震活动研究结果，本文模型的最小完备性震级M的取值为3.0，即以研究区域内3.0级以上的地震作为“异常学习”的信息输入。对于划分网格的长度△x，选用了0.1°×0.1°、0.2°×0.2°、0.3°×0.3°和0.4°×0.4°共4种网格尺度，使用Molchan图表法分别评价每种网格参数下RI模型的预测效能。用1970—2019年华北地区3.0级以上地震数据，以10a为异常学习时段预测未来5a的5.0级以上地震的效能评价结果，如图3a所示。图中彩色圆点为RI模型不同网格参数的Molchan图表法的结果，彩色实线代表RI模型不同参数的区域技能评分结果，虚线为显著性水平等值线，对角黑色实线为无预测技能分界线。0.1°×0.1°、0.2°×0.2°、0.3°×0.3°和0.4°×0.4°网格的预测效能评价分值依次为0.831、0.877、0.783和0.718，很显然0.2°×0.2°的网格是采用RI模型研究华北地区中强地震危险性的最佳网格尺度，在此参数下华北地区5.0级以上地震概率性危险区分布结果如图3b所示。图中颜色的深浅代表发生地震的危险性程度，颜色越深表示危险程度越高;蓝色圆圈为1980—1984年5.0级以上“目标地震”的实际发生位置，18次地震中，除位于125°E边界线上的1次地震外，其他均发生在危险程度较高的区域，预测效能相对较好。图3c是自1980年起，以10a为异常学习时段，用RI模型逐年回溯预测华北地区未来1a、3a和5a尺度5.0级以上地震的效能评价分值统计结果。由图可知，图3c中除有少数年份的分值低于0.4外，大多年份均大于0.6，且有多个年份大于0.9，总体水平相对较好。

对于MR模型，重要的计算参数是最小样本量n，和采样网格尺寸r。笔者依据研究区域3.0级以上地震的活动频次，设置初始最小样本临界值n，为5，即计算过程中，在每个单元格内要求存在至少5个3.0级以上的地震事件才可计算出该点的MR值，然后设置（0.1°x0.1°、0.2°x0.2°、、0.3° 0.3°和0.4.4°x0.4°）这4种不同的网格，同样应用Molchan图表检验法选出最优的网格尺寸r。每种网格的预测效能评价结果如图4a所示（图4中要素含义与图3相同），网格尺寸从小到大的评价分值分别为0.639、0.752、0.651和0.577。显然0.2°x0.2°网格的分值最高，在此参数下未来5a尺度5.0级以上地震的危险性分布如图4b所示。图中危险区域分布的整体趋势与图3b基本一致，但各具特点。在MR模型无震区发生的目标地震有2次，西边界高危无震区1处，且击中的地震中有4次的预测效能处在显著性水平α=1%的等值线以外;在标注的有震区内，颜色较深的高危区块较少，最明显的是河北平原地震带与张渤地震带相交的天津一唐山一带，其次是河北平原地震带与山西汾渭地震带的连接区，与RI模型的结果相比，该区的危险程度明显高于两侧。图4c为以10a为异常学习时段，3种不同时间尺度的MR模型效能评价分值统计图。1980—1991年因3.0级以上地震数量较多，预测效果相对较好，效能评分基本都在0.6以上;1992年以后因采样信息量较少，且发震位置分散，效能评分值相对较低。

在我国大陆地区的研究中，Triple -S模型运用最为广泛的平滑函数是Frankel （1995）提出的高斯核函数（毕金孟，2017）。笔者选取不同的平滑距离数进行评价，结果如图5a所示（图5中要素含义与图3相同），0.1°×0.1°、0.2°×0.2°、0.3°×0.3°、0.4°×0.4°网格相应评分依次为0.776、0.798、0.770和0.796。取效能评价最高分值对应的0.2°×0.2°网格和平滑半径a=100km，用Triple -S模型预测得到的华北地区5.0级以上地震概率危险性分布（图5b）。图5b中彩色标注的危险区域面积明显大于前2种预测模型面积，且图中颜色较深的高危险区全部包含了前2种预测模型的高危区域，在实际发生的18次“目标地震”中，除研究区域东西两条边界的2次地震外其余全部精准预测，且均位于log（N/N）≥-4.78范围内，发震位置相对集中。在以1a、3a和5a为时间长度的回溯预测效能评分统计（图5c）中，在有“目标地震”发生的年份里仅有3次低于0.6，整体预测结果具有很高的可信度。

选取1970—2019年华北地区3.0级以上地震数据，分别运用RI模型、MR模型和Triple -S模型，以10a为异常学习时段回溯性预测未来5a发生5.0级以上地震的危险区为例，对模型的网格划分和计算半径等参数进行了优化。在该预测时段内，3种模型在最优参数条件下的评分值依次为0.877、0.752和0.796，即RI模型优于Triple -S模型，Triple -S模型优于MR模型，且整体预测效能水平相对较高。

4构建混合模型分析地震活动特征

在最优参数条件下，3种模型的整体预测效能水平相对较高，但所预测的危险区域分布存在一定差异。分配不同的权重因子构建混合模型，可以放大单个模型的“优势”，缩小模型中存在的“劣势”。权重分配的大小取决于预测效能评价信息中数值的分布，即分值高且分布集中的模型赋予的权重大，反之权重小。本文运用T-test检验方法比较混合模型与单一模型的结果，通过调整权重因子，使混合模型结果达到最优状态，确定适合华北地区不同预测时间尺度的中强地震混合模型，并使用最近10a的地震数据计算中强地震的概率性危险区分布，分析当下华北地区的地震活动特征。

RI模型、MR模型和Triple -S模型对华北地区5.0级以上地震1a尺度的预測效能评分如图6a所示。由图可见，在41次计算结果中在研究区域内共有25次“目标地震”发生，其中RI模型评分最高的有10次，MR模型有5次，Triple -S模型有10次，分别占比40%、20%和40%。3种模型相对于零假设条件下的T-test检验结果如图7a所示，从图中可以发现，虽然RI模型和Triple -S模型的高分数量同样多，但Triple -S模型的评价分值分布最为集中，预测可信度高，即Triple -S模型优于MR模型，MR模型优于RI模型，所以Triple -S模型应该赋予最高权重。由于Triple -S模型在计算时受平滑半径参数的影响，危险区域呈圆（椭圆）形分布，需要有危险区域小且分值分布好的MR模型突显其中高危险性的重点区域。而RI模型又因其最高分值次数与Triple -S模型相同，且效能评分最为分散，所以应分配最低权重。因此，本文综合考虑3种单一模型的T-test检验结果和“目标地震”占比情况两个因素，确定华北地区1a尺度的混和模型的计算表达式为20%MR+80%Triple -S。

3种模型对华北地区5.0级以上地震3a尺度的预测效能评分统计中（图6b），研究区域内有30次“目标地震”发生，RI模型、MR模型和Triple -S模型分值最高的次数分别为12次、8次和10次，占比依次为40%、27%和33%。参照华北地区5.0级以上地震的时间分布（图2）可以看出，MR模型仅对2006年发生的1次地震预测效果明显，所以预测效能评分在该年前后最高，而RI和Triple -S模型无论是在地震频发时期，还是在地震较少时段，效能评分基本同步，且均好于MR模型。3种单一模型相对于零假设条件下的T-test检验结果如图7b所示，从整体来看，对于3a尺度的概率预测，Tri-ple-S模型优于RI模型，RI模型优于MR模型，因此MR模型在混合模型中应给予最低权重。5a尺度的预测效能评分统计（图6c、7c）与3a尺度的情况基本类似，RI、MR和Triple -S模型分值最高次数和占比分别为16次、5次、11次和50%、16%、34%。RI模型高分次数最多，但分值波动范围略宽，Triple -S模型虽然高值比例次之，但评价分值分布最为集中，而MR模型基本不占优势，不仅最高分值的次数少，而且大多的计算结果都明显低于前两种模型。综合以上分析，基于3种单一模型的T-test检验结果和“目标地震”占比分布情况的一致性，确定华北地区3a和5a尺度的混和模型计算公式统一表示为30%RI+70%Triple -S。

不同时间尺度的混合模型与RI、MR和Triple -S3种单一地震预测模型相对于零假设条件下的T-test检验结果如图7所示。从图中可以发现，在T-test检验结果中，混合模型与相对最优的Triple -S模型基本一致，且均明显好于RI和MR模型。

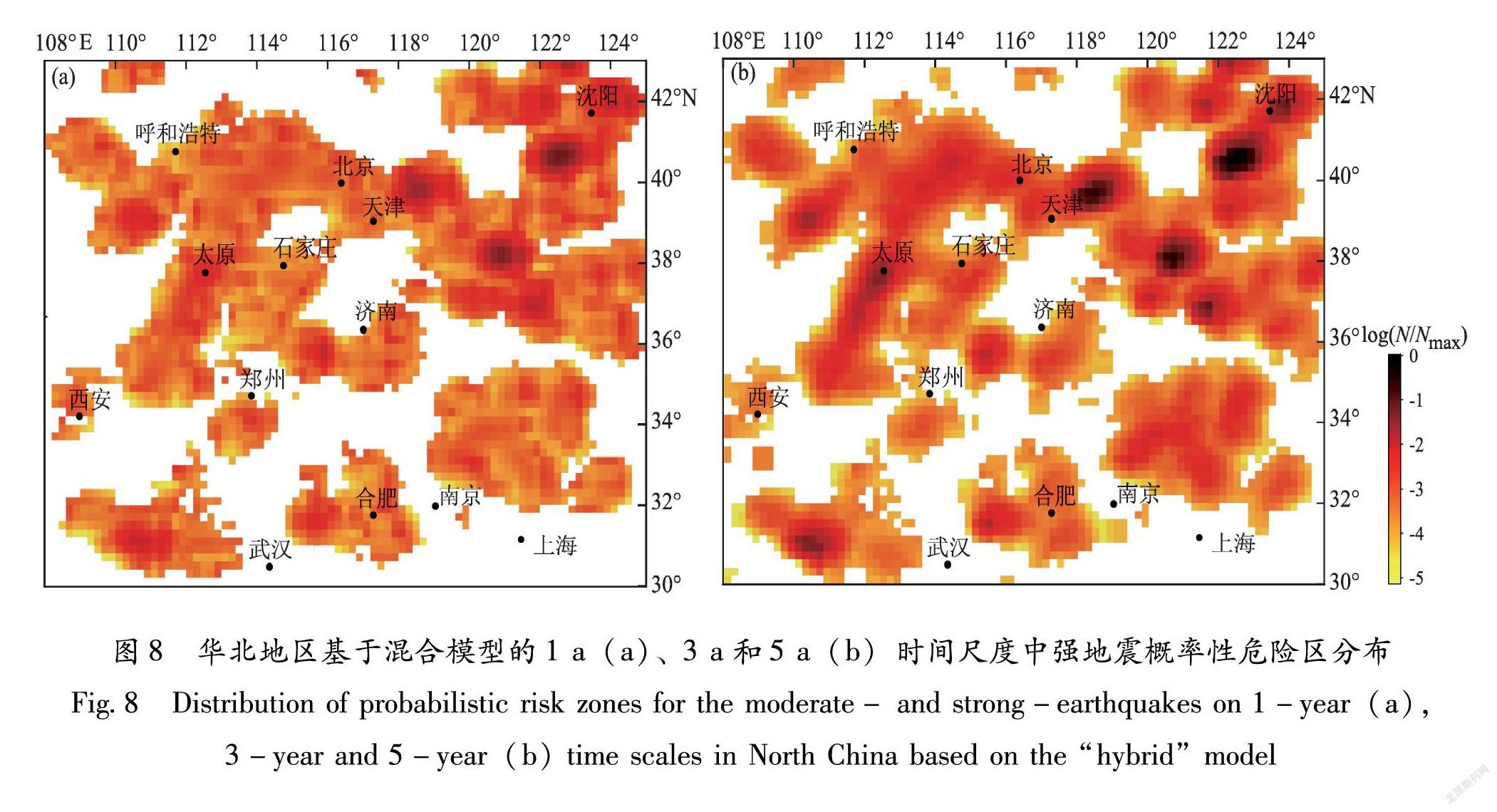
图8展示了基于前文的混合模型，以2010—2019年华北地区3.0级以上地震为异常学习时段得出的未来1a、3a和5a尺度发生5.0级以上地震概率性的危险区域。从图中可以看出因混合模型中包含其他模型的成分，在一定程度上改善了Triple -S模型危险区域呈圆（椭圆）形的分布情况，突出了其中高危险区域的重点位置，特别是在图8a中体现得尤为明显。根据“目标地震”在单一模型中的分布，需要重点关注log（N/N）高于-3.3和-3.6的区域。从总体分布来看，当前华北地区地震危险性最为明显的是山西汾渭断裂带和张渤地震带，其次是河北平原断裂带南部和郯庐断裂带中北段，零散块状区域为湖北北部和江苏东北部及其附近海域。在1a时间尺度图（图8a）中，发生中强地震的高概率危险区域主要有河北平原断裂带和张渤地震带交汇的唐山地区、郯庐断裂带北段的胶东半岛和辽东地区。2020年研究区域内共发生5.0级以上地震1次，即7月12日唐山古冶5.1级地震，位于图中的高危范围内。在图8b中，除以上3处重点区域外，还有山西断裂带中部、陕西北部、湖北宜昌和山东威海地区，这些区域活动断层发育、地震活动频繁。

5结论

本文以地質构造复杂、地震活动频发的华北地区为研究对象，使用1970—2020年华北地区3.0级以上地震数据，利用RI模型、MR模型和Triple -S模型3种单一地震预概率测模型，以10a为异常学习时段，以1a为分析步长，对5.0级以上地震分别开展1a、3a和5a尺度的回溯性滑动预测，并运用Molchan图表法和T-test统计检验方法进行预测效能评价;再参照效能评分优化模型参数，通过为每种单一模型分配不同权重因子的方式，构建了适合华北地区的中强地震混合模型，评估了当前华北地区的地震活动特征，得出以下几点认识：

（1）通过对比预测效能评价分值得出，在华北地区，使用3.0级以上地震，以10a为异常学习时段，开展5.0级以上地震概率预测研究时，RI模型、MR模型和Triple -S模型的最优参数设置分别为：最小震级为3.0，采样网格0.2°×0.2°;最小样本量为5，采样网格0.2°×0.2°;采样网格0.2°×0.2°，平滑半径为100km。

（2）根据3种单一模型最优参数时的T-test检验结果和“目标地震”占比分布情况，构建适合华北地区1a、3a与5a尺度的混合概率预测模型，计算表达式分别为20%MR+80%Triple -S和30%RI+70%Triple -S，模型预测效能检验结果得到明显改善。

（3）依照混合模型的计算公式，使用近10a的地震数据，获得当前华北地区中强地震概率性危险区分布，危险区分布与断裂带的活动断层展布一致，突出了其中高危险区域的重点位置，其中1a尺度的重点区域有3处，3a和5a尺度的重点区域共有7处。

在OEF研究的发展进程中，为决策者提供有价值的参考信息、为地震预测的实际应用和为社会公众服务等是亟待解决的重要问题。本文获得的华北地区概率预测模型最优参数、混合地震预测模型和地震活动特征，对该区域的地震预测预报研究和地震危险性评估都具有潜在的实际应用价值。在今后的工作中，将使用更多模型，对不同时段和地区开展更加深入、全面的研究。

感谢中国地震台网中心全国地震编目系统提供的数据支持，感谢审稿专家为本文提出的宝贵意见。

参考文献：

毕金孟，蒋长胜。2017。可操作的地震预测（OEF）国际研究动态综述[J].中国地震，33（1）：1-13。

毕金孟，蒋长胜。2019。华北地区地震序列参数的分布特征[J].地球物理学报，62（11）：4300-4312。

毕金孟。2017。区域地震预测策略和预测效能评价技术研究[D].北京：中国地震局地球物理研究所

蒋长胜，张浪平，韩立波，等。2011。中长期地震危险性概率预测中的统计检验方法I：Molchan图表法[J].地震，31（2）：106-113。

李三忠，张国伟，周立宏，等。2011。中、新生代超级汇聚背景下的陆内差异变形：华北伸展裂解和华南挤压逆冲[J].地学前缘，18（3）：79-107.

刘瑞丰，蔡晋安，彭克银，等。2007。地震科学数据共享工程[J].地震，27（2）：9-16。

刘瑞丰，高景春，陈运泰，等。2008。中国数字地震台网的建设与发展[J].地震学报，30（5）：533-539。

马干，史保平，凌华刚。2009。华北地区地震危险性分析和地面运动预测的一致性方法[J].中国地震，25（3）：303-313。

韶丹，贾宁，王莹。2015。陕西地区地震目录完整性分析[J].地震地磁观测与研究，36（4）：30-35。

王鹏，郑建常，赵金花，等。2011。山东地区最小完整性震级的确定—R-S检验[J].华北地震科学，29（3）：19-22。

王霞，宋美琴，李丽，等。2014。山西地区不同时段地震目录最小完整性震级研究[J].地震，34（2）：82-88。

谢卓娟，吕悦军，方怡，等。2019。京津冀地区的地震活动性研究[J].地球物理学进展，34（3）：961-968。

Field E H. Arrowsmith RJ.Biasi G P. et a.2014.Uniform California earthquake rupture forecast Version3 UCERF3）-The time - inde-pendent model[ J]. Bulletin of the Seismological Society of America 104（3）：1122-1180.

Frankel A.1995. Mapping seismic hazard in the central and eastern Unit-ed StatesJ]. Seismological Research Letters， 66：8-21

Jordan TH， Chen Y T， Gasparini P， et al.2011. Operational earthquake forecasting： State of knowledge and guidelines for implementation [J].AnnGeophys ，54（4）：315-391.

Jordan T H， Marzocchi W， Michael AJ， et al.2014.Operational earth-quake forecasting can enhance earthquake preparedness[].Seismo-logieal Research Letters.85（5）： 955-959.

Marzocchi w， Jordan T H.2014. Testing for ontological errors in probabi-listie forecasting models of natural systems[ J]. Proceedings of the National Academy of Sciences of the United States of America， 111（3）：11973-11978.

Molchan G M.1997. Earthquake prediction as a decision-making prob-lem[ J]. Pure and Applied Geophysics， 149（1）： 233-247.

Molchan G M.2010. Space-time earthquake prediction the error dia-gramsJ. Pure and Applied Geophysics， 167（8-9）： 907-917.

Nanjo KZ.2010. Earthquake forecast models for Italy based on the RI al-gorithm[ J]. Annals of Geophysics， 53（3）： 117-127

Nanjo KZ.2011. Earthquake forecasts for the CSEP Japan experiment based on the RI algorithm[ J]. Earth， Planets and Space， 63（3）： 26-274.

Rhoades DA.Gerstenberger M C.2009. Mixture models for improved short-term earthquake forecastingLJ. Bulletin of the Seismological Society of America， 99（2A）： 636-646.

TalbiA， Nanjo K， Zhuang J， et al.2013. Interevent times in a new alarm based earthquake forecasting model [ J]. Geophysical Journal In-temational.194：1823-1835.

Tiampo KF， Rundle J B， Meginnis S， et al.2002. Mean field threshold systems and phase dynamics： an application to earthquake fault sys-tems[ J].Europhysics Letters， 60（3）： 481-487.

Zechar JD， Jordan T H.2010. Simple smoothed seismicity earthquake forecasts for Italy[ J]. Annals of Geophysics， 53（3）： 99-105.

Analysis of the Seismicity in North China Using Hybrid Probability Forecasting Model

MA Yong， BI Jinmeng， SONG Cheng， SHANG Xiangi （Tianjin Earthquake Agency， Tianjin 300201， China）

Abstract

For the" Operational Earthquake Forecasting（ OEF） ， it is critical to build a predictive model that conforms to the regional seismicity and whose effectiveness can be evaluated. In this paper， we select the M>5.0 earthquake data from 1970 to 2019 in North China with complex geological structure and intensive earthquake activity， use the relative intensity （RI） model， the moment ratio （MR） model and the simple smoothing （Triple-S） model carry out a retrospective sliding prediction of the historical M>5.0 earthquakes， during which we set the " learning period of earthquake anomalies as 10 years， step length as I year， and the scale of the retrospective cycle as I 3 and 5 years. Then we use the Molchan Diagram method and the T-test method to evaluate the efficacy of the pre-diction model. We determined the best calculation parameters of the three prediction models by optimization， and constructed a " hybrid" of probability forecasting models on different time scales which is suitable for analyzing the characteristics of earthquake activity in North China. Then we apply the latest 10-year earthquake data to our mod-el for the analysis of the current characteristics of earthquake activity in North China.

Keywords： probability forecasting model; effectiveness evaluation; characteristics of earthquake activity;NorthChina