传热学一维非稳态导热内容分解
2021-09-22吴春梅李友荣
吴春梅 李友荣
摘 要:基于传热学的分级教学理论,提出了分级教学中一维非稳态导热教学内容的分解原则,即在初级层次教学中主要讲授一维非稳态导热海斯勒图的构成及其应用,在专门层次教学中主要讲授求解一维非稳态导热的近似计算公式;同时,以典型的一维非稳态导热过程为例对此进行了详细的阐述。多年的教学实践表明,这种非稳态导热教学内容的分解方法可以满足工科类不同专业、不同层次的教学需求。
关键词:传热学; 分级教学; 非稳态导热; 教学内容
中图分类号:G64 文献标识码:A 文章编号:1006-3315(2021)11-156-002
传热学是研究热量传递规律的科学,它几乎涉及到所有的工程技术领域,特别是在能源、化工、冶金、建筑、航空航天、交通运输和生物技术等领域更是有着广泛的应用[1-2],因此,在高等学校的很多工科专业,都开设有传热学或热工基础课程,各高校都对传热学的教学内容和教学方法进行了很多有益的探索[3-6]。但是,由于不同专业所面对的工程问题不同,对所要求的传热学知识也有所侧重[7-9],因此,我们提出了传热学分级教学的理论[10]。
在针对本科生的传热学分级教学中,将传热学分成了传热学Ⅰ和传热学Ⅱ两部分,其中,传热学Ⅰ面向全校本科相关工科专业学生,主要目的是使学生通过学习获得必要的热量传递的基本理论、基本知识和基本技能,以及传热计算的基本方法,同时培养学生分析和解决实际传热问题的能力,为学生后续课程的学习和独立解决本专业所遇到的热工问题打下必要的基础。传热学Ⅱ主要面向对传热学有更高要求的专业,目的是培养学生独立分析和解决与专业背景相关的实际传热问题的能力,为学生后续课程的学习和从事相关专业技术工作打下必要的基础。传热学分级教学既保证了全校性热工基础类课程的普遍性,又满足了不同专业进一步深入学习传热学知识的特殊性,有效地利用了资源。
在传热学的分级教学中,教学内容的分解与取舍是至关重要的,它直接影响着分级教学的成败。一维非稳态导热是一种最常见的传热现象,求解一维非稳态导热问题的理论方法是分离变量法,得到的温度分布是一个无穷级数,不便于工程计算,因此,在理论分析解的基础上,产生了各种解的简化近似表达方式。本文基于传热学分级教学理论,提出了分级教学中一维非稳态导热教学内容的分解原则。
一、一维非稳态导热教学内容分解原则
在导热问题中,如果温度场不随时间发生变化,称之为稳态导热,反之,如果温度场随时间不断变化,则为非稳态导热。非稳态导热过程可以分为两个阶段,第一阶段是过程开始后的一段时间,称为非正规状况阶段,其特点是温度变化从导热体的表面逐渐深入到物体内部,物体内各点的温度随时间的变化率各不相同,溫度分布主要受初始温度分布的影响;随着导热过程的不断进行,初始温度分布的影响逐渐消失,进入到过程的第二阶段,即正规状况阶段,此时,物体内的温度分布主要受热边界条件的影响。
在非稳态导热过程中,根据温度随空间的变化规律不同,又可分为一维非稳态导热、二维非稳态导热和三维非稳态导热,其中,二维和三维非稳态导热统称为多维非稳态导热。因此,在传统的传热学教学中,非稳态导热教学内容主要包括三部分,即不考虑温度空间变化的集总参数系统、一维非稳态导热和多维非稳态导热。在分级教学中,可以将集总参数系统的教学归于传热学Ⅰ中,而将多维非稳态导热问题的乘积解法归于传热学Ⅱ中。然而,由于一维非稳态导热的教学内容较多,解的表达形式也有多种,理解的难度差异也较大,因此,必须要在传热学Ⅰ和传热学Ⅱ的教学中对一维非稳态导热的教学内容进行合理的分解。
本科学生在开始传热学Ⅰ的学习时,仅具备了普通物理、工程热力学和工程流体力学等方面的基本知识,因此,传热学Ⅰ中关于一维非稳态导热教学内容的选择应遵循浅显易懂、便于理解的原则;在学习传热学Ⅱ时,学生已掌握了传热学的基本概念及基本定律,因此,关于一维非稳态导热教学内容的选择应遵循精确计算、简便实用的原则。
二、海斯勒图的构成及应用
在传热学Ⅰ中,非稳态导热的教学总是从集总参数系统开始的[11]。假设某物体的体积为V、表面积为A,初始温度为t0。在初始时刻,将该物体置于温度为t∞的流体介质中冷却,已知物体表面传热系数为h,物性为常数,且物体内部热阻可忽略不计,则物体的温度仅随时间变化。在非稳态导热集总参数系统的教学中,必须要反复向学生强调,当忽略内阻时物体的无因次温度Θ=θ/θ0仅与两个无因次参数Bi数和Fo数有关。
对一维非稳态导热问题而言,与集总参数系统最大的不同是物体内部的温度还随一个方向的空间位置发生变化。例如,对于一块厚度为2δ的大平板,设其初始温度为t0,在初始瞬间将其置于温度为t∞的流体中冷却,平板两侧表面传热系数都为h,因此,平板内部的温度是关于平板中心对称的,为此,将x轴的原点置于大平板的中心处,并定义无因次坐标η=x/δ,则大平板内的无因次温度分布一定只与三个无因次参数相关。
上述温度分布函数可以通过分离变量法对大平板内一维非稳态导热理论模型求解获得。但是,在传热学Ⅰ的教学中,不涉及到复杂的求解过程,只专注于解的图示表述,即海斯勒图的构成与应用。
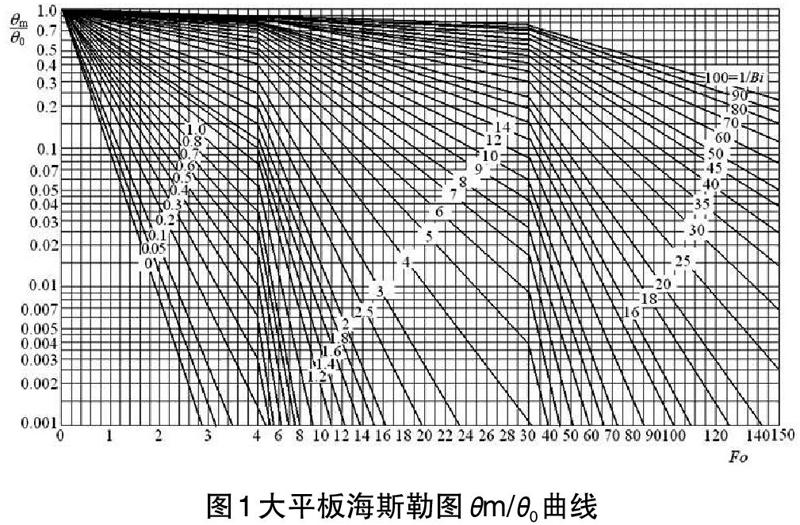
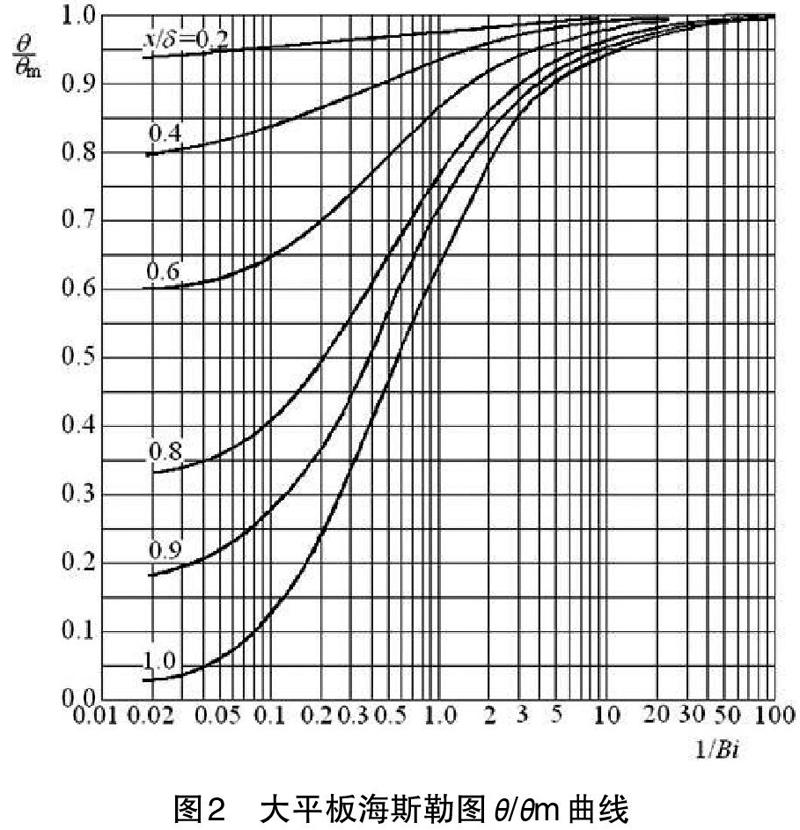
由于温度变化规律是三个无因次参数的函数,不可能在一个平面图上表述包含三个变量的函数关系。但是,通过对用分离变量法得到的解的计算结果表明,当Fo>0.2后,非稳态导热过程进入到正规状况阶段,此时,平板内任意点处的过余温度与平板中心处的过余温度θm之比与Fo数无关,因此,可以将无因次温度分解,这样θ/θm和θm/θ0就都只与两个变量有关,可以在平面图上表示。因此,用分离变量法得到的一维非稳态导热问题的分析解就可以用关于θ/θm和θm/θ0的两组线图来表示,这些线图就称为海斯勒图。
三、一维非稳态导热的近似公式
当学生在学习了传热学Ⅰ、了解了海斯勒图的构成后,自然会产生这样的疑问:由于查海斯勒图时误差较大,因此,是否存在便于计算、精度较高的公式呢?回答是肯定的,这就是一维非稳态导热的近似公式,它是传热学Ⅱ中非稳态导热的主要教学内容,包括用分离变量法求解一维非稳态导热问题的过程、解的近似方法以及拟合公式等。
为了与传热学Ⅰ的教学内容相衔接,仍以大平板内的一维非稳态导热过程为例[12],在教学过程中,重点是分离变量法求解一维非稳态导热问题的基本思想:即将温度随时间和空间的变化规律分离成两个分别随时间和空间变化的单元函数的乘积,然后代入导热微分方程得到关于这两个单元函数的常微分方程后分别进行求解。将求得的两个单元函数按照分离变量的形式相乘、并叠加起来,最后利用初始条件就可得到温度分布。对于大平板内的一维非稳态导热过程而言,无因次温度分布的解析解为一无穷级数之和,且只与三个无因次参数,即Fo数、Bi数和无因次距离η有关。
总之,在关于一维非稳态导热问题的教学内容安排上,应该重点针对大平板内的一维非稳态导热过程,使学生了解用分离变量法求解的过程以及近似公式获取的方法,并要求学生针对具体的一维非稳态导热问题计算级数解中每一项的相对大小,以便加深对近似公式的理解。另一方面,也可要求学生对同一非稳态导热问题分别用海斯勒图和近似公式求解,并对结果进行分析比较,促使学生更进一步的思考。
四、结束语
由于传热学广阔的工程应用,本文提出的传热学一维非稳态导热教学内容的分解原则是行之有效的,即在传热学Ⅰ中主要讲授一维非稳态导热海斯勒图的构成及其应用,在传热学Ⅱ中主要讲授一维非稳态导热问题的近似计算公式。这种非稳态导热教学内容的分解方法不仅可以加深学生对一维非稳态导热过程的理解,激发学生的学习兴趣,而且可以满足工科类不同专业的教学需求。
参考文献:
[1]杨世铭,陶文铨.传热学(第四版)[M]北京:高等教育出版社,2006
[2]戴锅生.传热学(第二版)[M]北京:高等教育出版社,1999
[3]刘爱萍.浅谈传热学课程的教学改革[J]中国电力教育,2002(4):73-75
[4]赵忠超,周根明,唐春丽.基于CDIO理念的传热学课程教学研究与探讨[J]高等建筑教育,2014,23(1):79-82
[5]李友荣,吴双应.传热学教学中的热路分析法[J]高等建筑教育,2012,21(1):51-53
[6]刘鸿.《传热学》课程的教学探讨[J]教育教学论坛,2014(6):160-161
[7]李友荣,杨晨,吴双应,彭岚.“传热学”课程教学改革研究与思考[J]中国电力教育,2010(32):66-67
作者简介:吴春梅,1987年生,女,教授,主要从事传热传质学方面的教學和研究工作。
