旋转超声磨削平行砂轮复合变幅器设计与试验∗

2021-09-22周瑞峰秦慧斌庞学慧

应用声学 2021年4期

周瑞峰秦慧斌冯毅庞学慧吕明

(1 中北大学先进制造技术山西省重点实验室太原 030051)

(2 太原理工大学精密加工山西省重点实验室太原 030024)

0 引言

旋转超声磨削加工技术具有切削力小、加工损伤少、加工效率高的优点，适用于工程陶瓷、光学玻璃、金属基复合材料等硬脆性材料的加工[1−2]。超声谐振刀具系统是超声磨削工艺系统的核心，它的性能直接影响着硬脆材料的加工质量和使用性能[3−4]。目前大负载旋转超声加工谐振系统的设计缺乏系统的理论设计方法，谐振系统设计周期长、试用性差[5]。

超声磨削工具系统主要有将超声振动作用于工件或砂轮两种方式[6−7]。文献[8]基于Mindlin理论提出了齿轮变幅器的设计方法，完成了齿轮超声珩磨，但超声谐振施加在齿轮工件上，工艺通用性不足。赵波等[9]将超声振动施加在短粗圆柱砂轮上，设计的超声辅助内圆磨削工具系统具有良好的声学特性。平行砂轮超声磨削谐振系统的核心部件是平行砂轮谐振变幅器，它由变幅杆和平行砂轮组成。付俊帆等[10]基于Mindlin 中厚板理论提出了环盘负载与圆锥变幅杆的纵弯谐振变幅器设计方法，但尚未应用于旋转超声磨削工具系统的设计。圆柱与圆锥形的复合变幅杆在大功率超声应用中，其圆锥输出端往往具有较大的振幅、较小应力等优点，并且该种变幅杆在加工和安装方面更具便利性[11]。复合变幅杆与平行砂轮组成的复合变幅器在旋转超声磨削中具有更广泛的工艺适应性。

本文以设计大负载平行砂轮复合变幅器为目的，采用Mindlin 中厚板理论，通过复合变幅杆各段间的力与位移的边界条件和连续条件，环盘的位移、转角、弯矩和剪力的解析表达式，以及复合变幅杆和环盘力与位移的耦合条件，建立平行砂轮复合变幅器的数学模型与频率方程。利用有限元方法分析复合变幅器的谐振频率及模态，并加工实物进行阻抗试验和超声谐振试验，来验证理论设计方法的可行性。

1 复合变幅器的设计理论分析模型

1.1 平行砂轮旋转超声磨削刀具系统

由于平行砂轮可用于内圆磨、外圆磨、平面磨、无心磨和装在砂轮机上手动粗磨等多种提高零件表面质量的工艺中，因此，将平行砂轮结合超声振动用于磨削领域。为了提高旋转超声磨削刀具系统在磨削工艺中的通用性，设计了一种可以应用于标准加工中心或通用机床上的旋转超声磨削刀具系统，其中平行砂轮旋转超声磨削刀具系统由BT40 标准刀柄设计的刀柄套筒、导电滑环、锁紧螺母、超声波振子以及平行砂轮组成，其装配体如图1所示[12]。

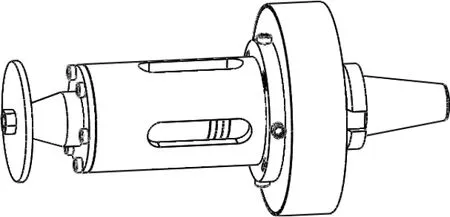
图1 刀具系统的装配体模型[12]Fig.1 Assembly model of the tool system[12]

该刀具系统的爆炸图如图2所示，由锁紧螺母、平行砂轮、内六角固定螺栓、复合变幅杆、换能器、BT40 刀柄套筒、转子固定螺栓、导电滑环这8 部分组成，其中锁紧螺母、平行砂轮、复合变幅杆、换能器组成了旋转超声磨削刀具系统的核心部件——平行砂轮复合变幅器。超声波振子由换能器和复合变幅杆组成，超声波能量从超声波发生器输出电信号，流经导电滑环的导线将电信号传递至换能器，换能器将电信号转变成机械振动，再利用复合变幅杆放大的作用将机械振动放大，最终传递至平行砂轮使其产生超声磨削所需的高频振动，为旋转超声磨削加工提供能量。

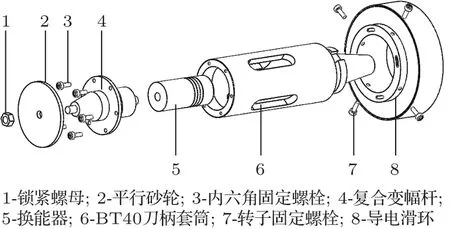
图2 刀具系统的爆炸图模型Fig.2 Exploded view model of the tool system

20 kHz、28 kHz、35 kHz 的系列超声发生器、换能器等成熟产品已投放市场，为旋转超声磨削加工的砂轮谐振变幅器的研制提供了物质保障。论文基于市场上成熟的28 kHz 超声发生器、换能器产品，设计旋转超声磨削平行砂轮复合变幅器。

1.2 复合变幅器的结构分析

利用大端为圆柱杆和小端为圆锥杆组合而成的复合变幅杆，通过薄螺母将砂轮环盘紧固于复合变幅杆的圆锥杆的小端组成了复合变幅器，如图3所示。由于薄螺母的尺寸相对环盘和复合变幅杆很小，所以在计算中忽略薄螺母对计算结果的影响。建立复合变幅器的圆柱坐标系(r,θ,z)如图3所示。其中，复合变幅杆的圆柱杆半径为R1，圆锥杆小端半径为R2；圆柱杆的杆长为L1，圆锥杆的杆长为L2；平行砂轮内孔半径、平行砂轮金属基体内环盘半径、中间环盘和磨料层环盘半径分别为R3、R4、R5、R6；各环盘厚度分别为t1、t2、t3。平行砂轮金属基体环盘的密度、弹性模量和泊松比分别以ρ1、E1、µ1表示，平行砂轮中间环盘的密度、弹性模量和泊松比分别以ρ2、E2、µ2表示，平行砂轮磨料层环盘的密度、弹性模量和泊松比分别以ρ3、E3、µ3表示，复合变幅杆的密度、弹性模量和泊松比分别以ρ4、E4、µ4表示。

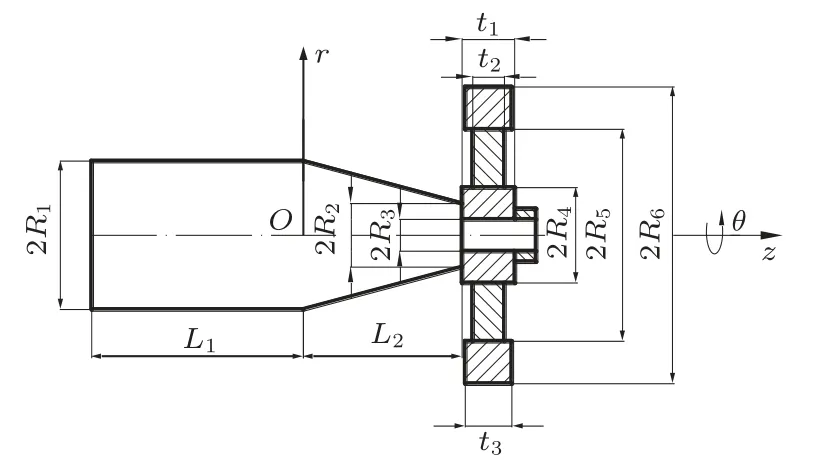
图3 复合变幅器理论分析模型Fig.3 Structure of the composite amplitude transformer

上述复合变幅器的理论模型是针对不同结构的平行砂轮的最大化的模型；若t1=t2=t3时，该理论模型可以设计求解相同厚度环盘的平行砂轮复合变幅器。若t1≠t2≠t3时，该理论模型也可进行不同厚度阶梯环盘砂轮复合变幅器的设计求解。该理论模型对旋转超声磨削刀具系统的研制具有重要的指导意义。旋转超声磨削平行砂轮复合变幅器以“纵-弯”耦合谐振方式工作。复合变幅杆的圆柱杆端与换能器相连接，换能器产生的纵向振动直接传递给复合变幅杆，复合变幅杆的纵向振动激励砂轮环盘以节圆型横向弯曲的振动形式作用于工件。

1.3 复合变幅器频率方程的建立与求解

1.3.1 复合变幅杆

复合变幅杆在其工作频率f下做纵向振动。圆柱杆的纵向振动位移以ξ1表示，应变以ε1表示；圆锥杆的纵向振动位移以ξ2表示，应变以ε2表示。ξ1、ξ2、ε1、ε2的解析表达式分别为

圆柱杆：

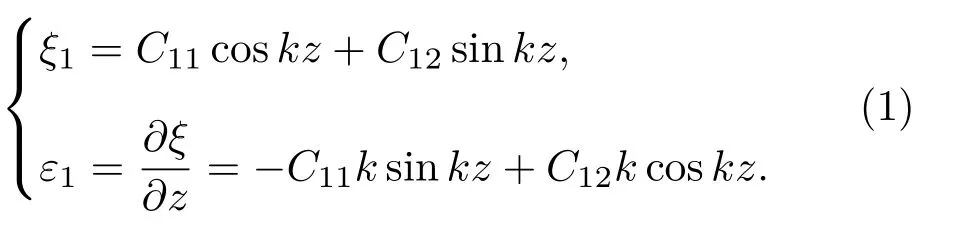
圆锥杆：

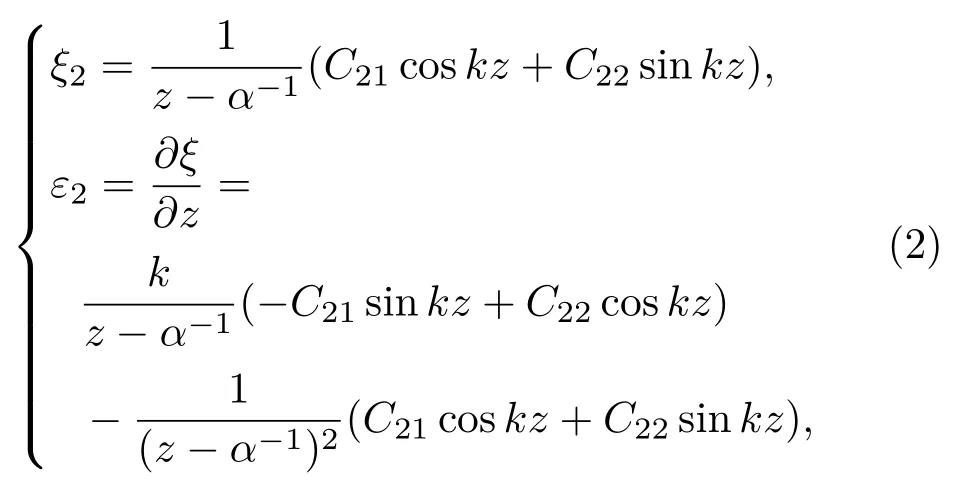
其中：α=(R1−R2)/R1L2；C11、C12、C21、C22为待定常数，由边界条件确定；圆波数k1、圆频率ω、纵波波速c1的计算公式为k1=ω/c1,ω= 2πf,

1.3.2 环盘

理论分析时，将平行砂轮简化为多阶梯环盘。环盘在复合变幅杆纵振激励下以节圆型横向弯曲振动形式做超声振动。各环盘的横向位移wi和径向转角βri的解析表达式[13]为

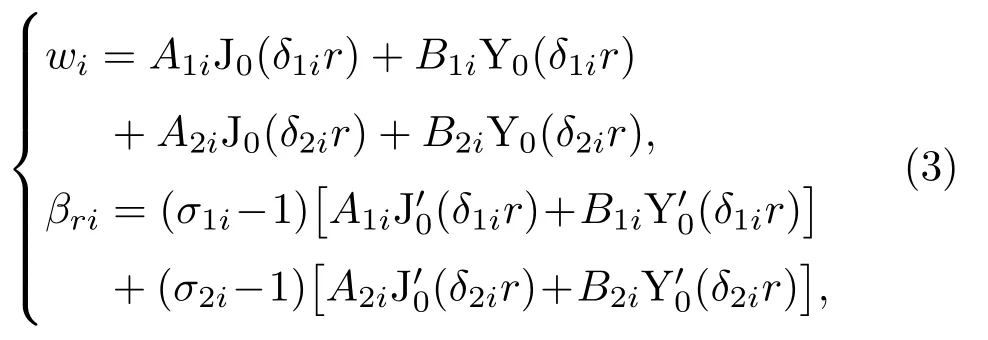
其中，A1i、A2i、B1i、B2i为由边界条件确定的待定常数，i= 1、2、3 分别表示内环盘、中间环盘和外环盘；Jn为第一类贝塞尔函数，Yn为第二类贝塞尔函数，n代表环盘振动的节径数，根据Mindlin 中厚板理论可以得出，环盘做节圆型横向弯曲振动，此时，n=0。式(3)中σ1i、σ2i、δ1i、δ2i可由式(4)求得如下：

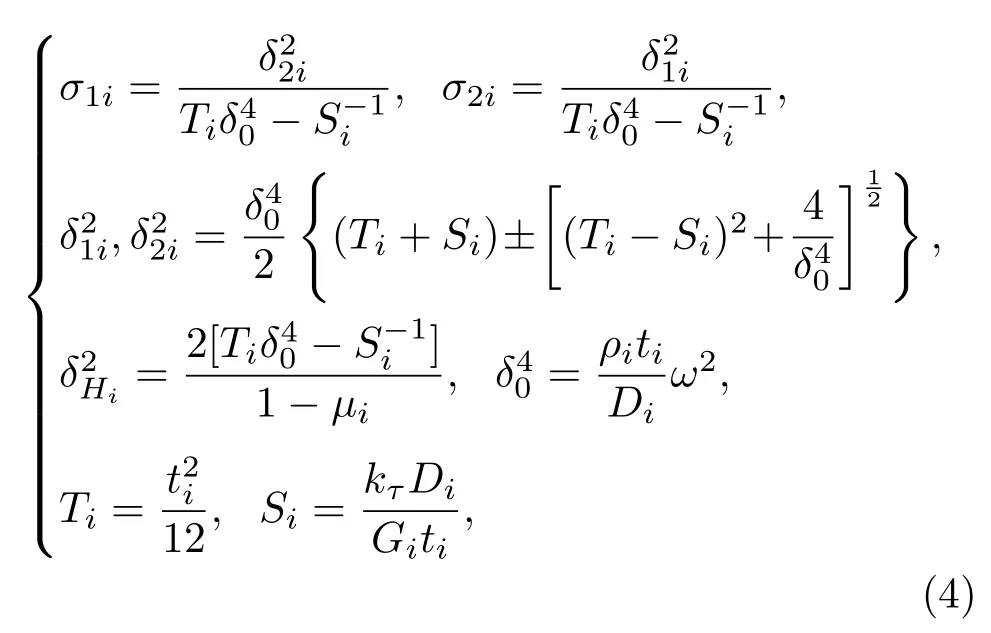
其中，材料的弯曲刚度、剪切弹性模量、剪切影响因子分别为

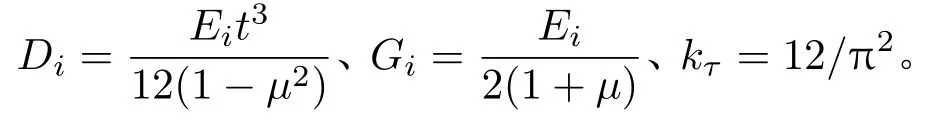
径向弯矩分量Mri和径向剪力分量Qri的解析表达式分别为

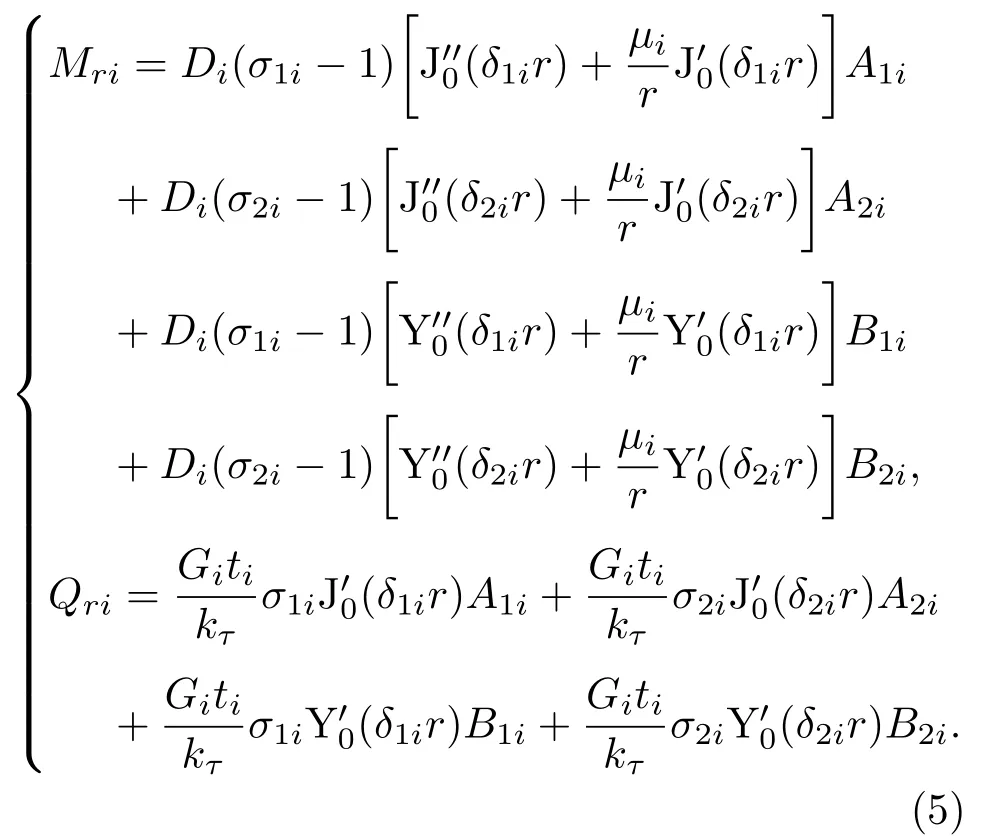
1.3.3 频率方程

与换能器相连接的复合变幅杆，在换能器的激励下做纵向振动，由于复合变幅杆圆柱端通过螺纹紧固在一起，换能器与圆柱端可以视为等能量传播，在复合变幅杆z=−L1处为自由端，应力为0，即

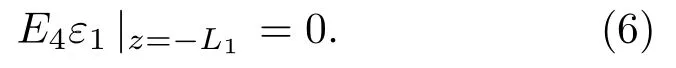
其中，在复合变幅杆的圆柱端和圆锥端之间由于存在截面变化，两部分在z=0处耦合，满足连续条件，即

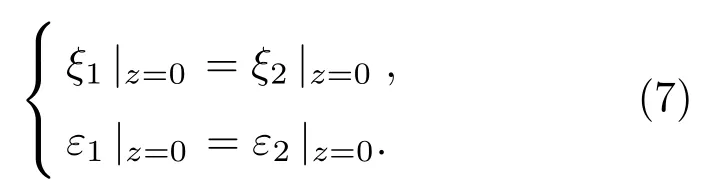
复合变幅杆的圆锥杆端与内环盘通过薄螺母紧固，可以视之为刚性连接。故在z=L2、r=R2处，复合变幅器上存在着圆锥杆小端与内环盘环形面沿z轴方向的力与位移的连续条件；由于复合变幅器整体为刚体，内环盘不存在转动，故在r=R3处，内环盘上的径向转角βr1为0，即

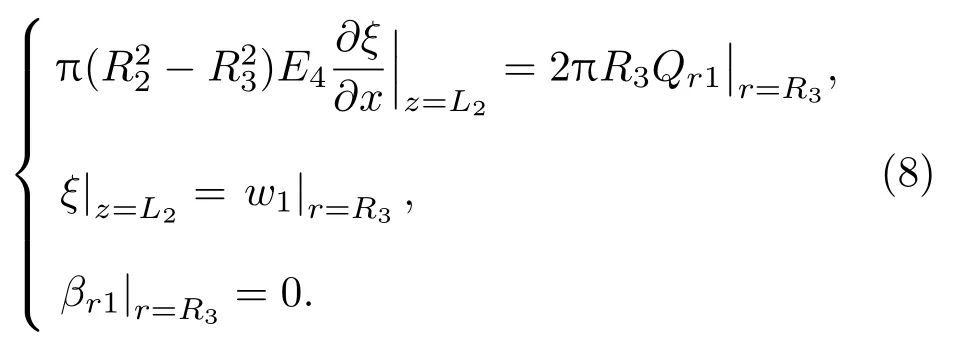
在复合变幅器的内环盘与中间环盘在r=R4处存在耦合，为满足两环盘之间的连续条件，横向位移wi、径向转角βri、径向弯矩分量Mri和径向剪力分量Qri相等，即

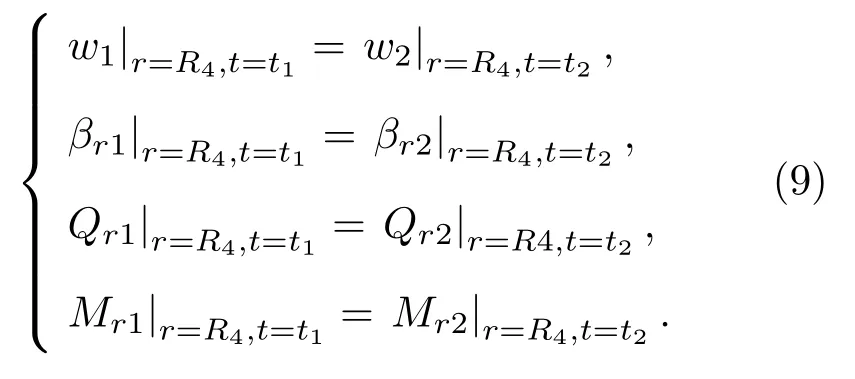
同样地，在复合变幅器的中间环盘和外环盘在r=R5处也存在耦合，因此在中间环盘和外环盘的连续条件，同样满足横向位移wi、径向转角βri、径向弯矩分量Mri和径向剪力分量Qri相等，即

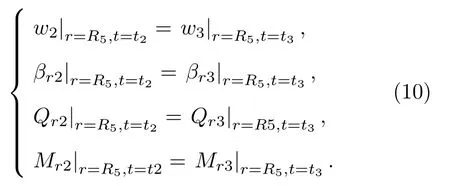
旋转超声磨削加工中，砂轮在切削工件时为高频非连续性接触，且磨削力会随磨削条件不同而改变；结合工作频率20 kHz 超声磨削振动系统的加工试验，磨削力负载对超声振动系统的设计可以忽略，因而视外环盘为自由边界，即

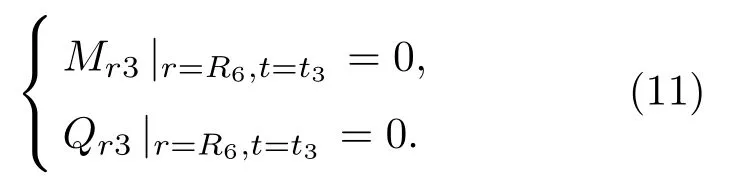
将式(6)～(11)整理，得到了一个16 阶的齐次方程组：

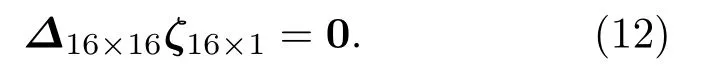
通过求解该方程组，可解得所需的参数。

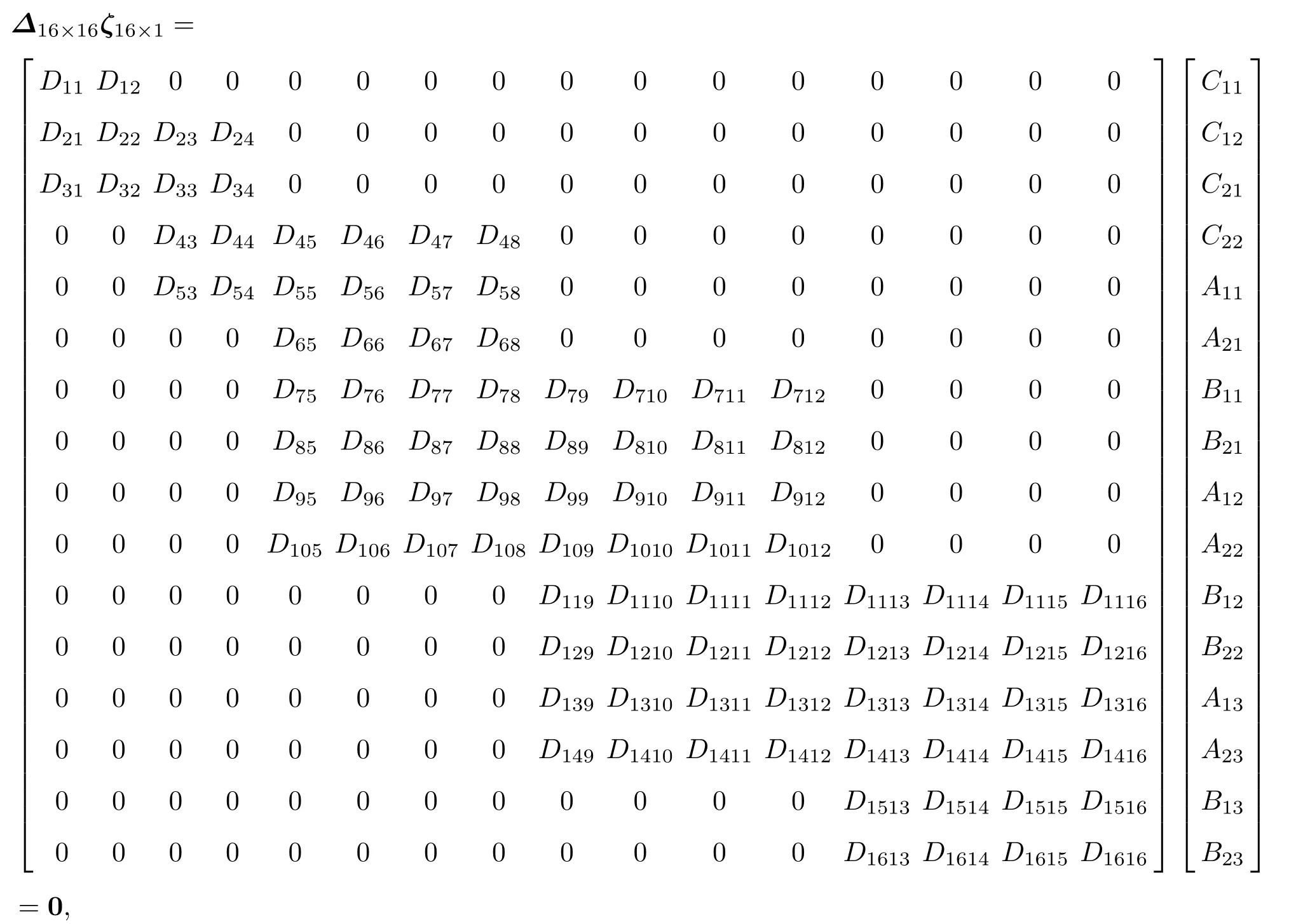
其中，Dpq(p、q= 1,2,3,···,16)均为待定常数，系数Cmn(m= 1,2;n= 1,2)可由复合变幅器的各项材料参数、尺寸参数和设计频率来确定相应的待定常数。其中系数A1i、A2i、B1i、B2i、Cmn不全为0时，要使得上述方程组有解的充要条件是由方程组系数组成的行列式|∆16×16|= 0，即可得到复合变幅器的频率方程。当确定了复合变幅器组成材料和各结构的尺寸参数时，可通过计算机编程对该频率方程求解得出复合变幅器的纵弯谐振频率。反之，当确定了复合变幅器的谐振频率、材料组成，通过各材料的性能参数以及变幅器的尺寸参数，同样对频率方程求解得出相应的未知尺寸。

显然，式(12)解得的解向量不唯一。因此，需要引入新的边界条件：其中换能器将超声振动的能量传递到复合变幅器圆柱端面上，可将换能器的输出振幅设为ξ0。此时，复合变幅器的圆柱端面处的边界条件即有

联立式(12)和式(13)可以得到方程组的唯一解向量，将这组解向量代入式(1)和式(2)，可以得到复合变幅杆的振幅曲线。同理，将这组解向量代入式(3)可求得各环盘的振幅曲线，也可以得到环盘上的各个位置的振幅曲线。

2 复合变幅器的结构设计

为了使这一设计理论方法更高效率地设计平行砂轮复合变幅器，利用计算机软件开发了平行砂轮复合变幅器尺寸设计软件，来求解复合变幅器圆锥杆部分的尺寸L2，其中复合变幅杆的材料为45#钢，平行砂轮由铝基体和金刚石磨料两种材料组成，各部分材料的性能参数如表1所示，将各部分材料的性能参数输入复合变幅器尺寸设计软件。

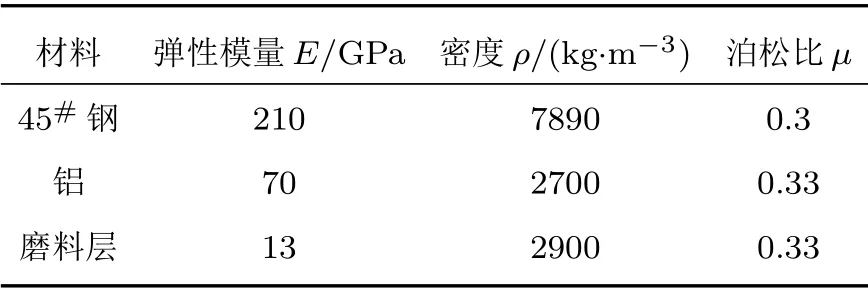
表1 材料的性能参数Table 1 Material performance parameters

在考虑了复合变幅杆的加工和安装等条件后，确定了复合变幅杆圆柱端的长度L1= 62 mm、R1= 20 mm、R2= 10 mm、R3= 5 mm。砂轮选用了市场上现有的平行砂轮，确定了平行砂轮的尺寸参数，其中内环盘、中间环盘的半径R4=R5=45 mm，内环盘、中间环盘即可合并成为一个环盘，各个环盘厚度t=t1=t2=t3=5 mm。将表2中复合变幅器的尺寸参数输入至开发的设计软件中，求解得到了复合变幅杆长度L2= 36 mm。将该尺寸的变幅器进行了模态分析得到的谐振频率为27494 Hz，由于该数值不在换能器的谐振频率的27752～30472 Hz 之间，因此在不改变复合变幅杆直径和大端的条件下，适当缩短其锥形杆部分的长度，最终在L2=30 mm时，进行模态分析得到复合变幅器谐振频率为28756 Hz，接近换能器谐振频率的中间值，此时的模态为“纵-弯”耦合的振动形式。因而将通过求解软件得到的L2取整为30 mm。

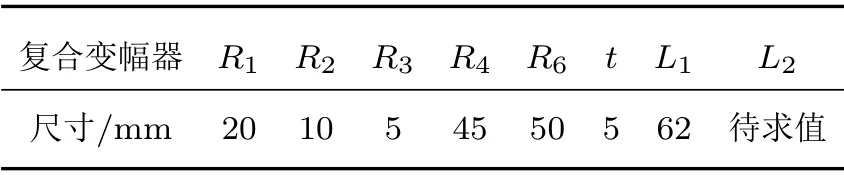
表2 复合变幅器的尺寸参数Table 2 Size parameters of the composite amplitude transformer

将上述各材料的性能参数和复合变幅杆各部分结构的尺寸参数带入式(12)和式(13)可求解得到平行砂轮复合变幅器振幅曲线。通过计算机软件编写了对应的求解程序，求解了平行砂轮复合变幅器砂轮的振幅曲线。试验设备所用的设备是杭州成功超声设备有限公司生产的超声波电源(型号YPJ17-0067)和柱形换能器(型号YP-3828-4BZ)，超声波电源正常的工作电压为220 V，最大功率为1000 W，超声波电源在工作电压下产生电激励通过柱形换能器产生高频振动，换能器端面处的输出振幅为6 µm，即ξ0= 6 µm，将其代入式(13)通过求解程序求得的平行砂轮在轴向方向的理论振幅曲线如图4所示，此时平行砂轮沿复合变幅器的轴向方向的振幅范围为−10～5 µm，在节圆半径r1= 26.12 mm、r2= 43.72 mm 处的轴向振幅为0，砂轮外缘的轴向振幅约为6 µm。为进一步验证该种理论设计方法的可行性，依据复合变幅器的设计结果加工了实物进行实验分析。

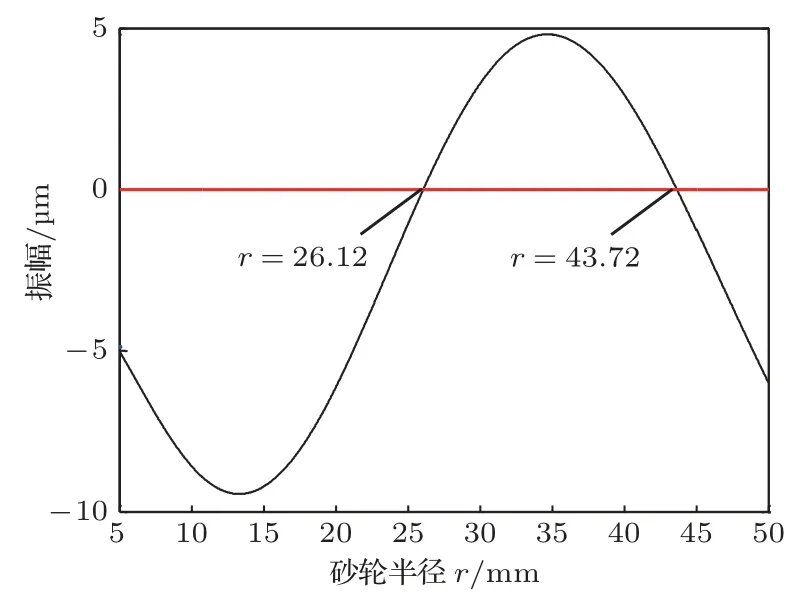
图4 平行砂轮理论振幅曲线Fig.4 Theoretical amplitude curve of parallel grinding wheel

3 复合变幅器的有限元仿真分析

依据表2中的复合变幅器尺寸参数通过Solid-Works 软件建立了三维模型，将建立好的三维模型导入有限元分析软件进行了模态分析。根据复合变幅器的各部分的材料参数设置了相应的材料属性，其中复合变幅杆的材料为45#钢，砂轮金属基体环盘的材料为铝，砂轮外环盘的材料为磨料层，并利用网格划分功能对各部分实体结构进行了4 级精度的智能网格划分，解法并提取25～30 kHz 的复合变幅器谐振状态。复合变幅器的有限元模态分析结果如图5(a)所示，砂轮的振动方向沿着复合变幅杆的轴向产生高频振动；其谐响应结果如图5(b)所示，并将法兰盘设置在复合变幅杆振幅节点位置如图5(b)所示，距复合变幅杆的圆柱末端45 mm，目的是降低法兰盘对复合变幅器振动效果的影响，并从图5(b)中可以得到复合变幅杆的轴向振幅大小约为−9～6 µm。其中，复合变幅器处于谐振状态是的频率为28756 Hz，该谐振频率与设计频率28000 Hz 的误差为2.7%。通过上述有限元模态分析的结果表明，通过该方法设计的平行砂轮复合变幅器振型良好，所以可以加工实物进行进一步的试验分析。

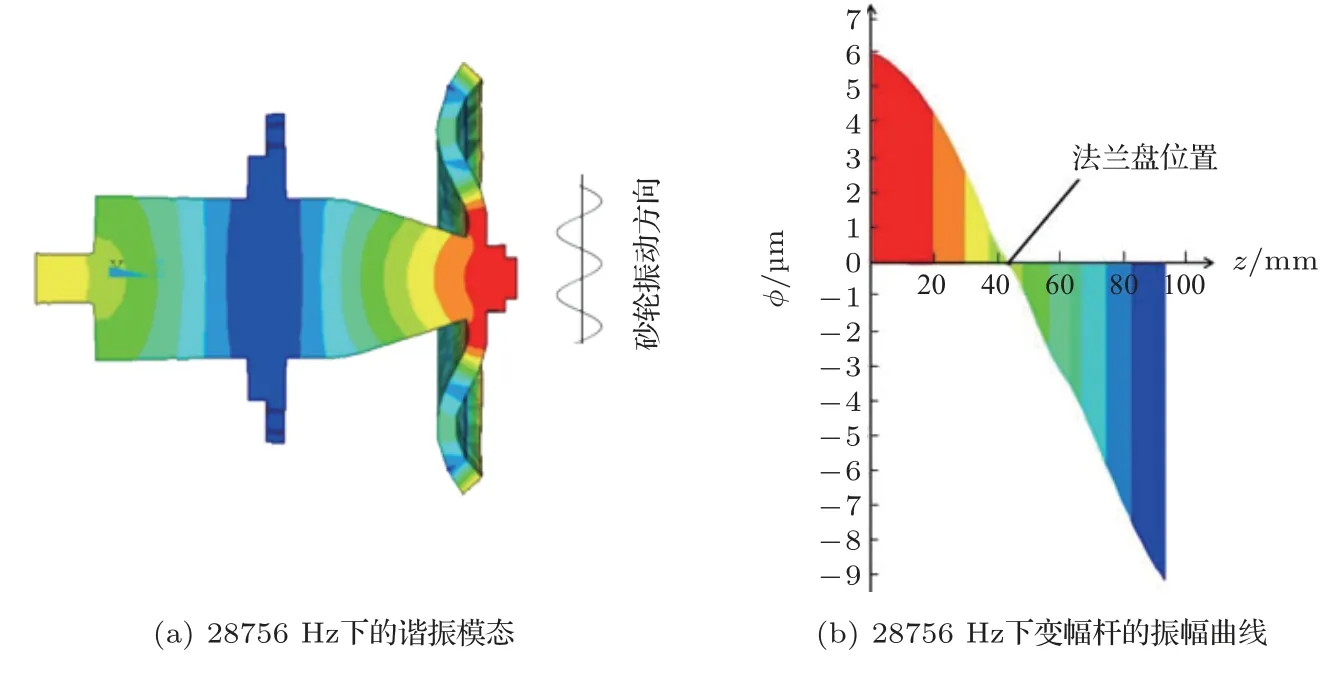
图5 复合变幅器Fig.5 Composite amplitude transformer

在确定了平行砂轮复合变幅器的结构和尺寸等参数后，通过有限元分析软件进行了谐响应分析，取该变幅器圆柱输入端的振幅为6 µm，得到了平行砂轮沿复合变幅器轴向方向的振幅曲线如图6所示，此时平行砂轮的轴向振幅为−10～5 µm，在节圆半径r1=27.13 mm、r2=44.57 mm 的轴向振幅为0，环盘外缘的的轴向振幅约为7 µm。

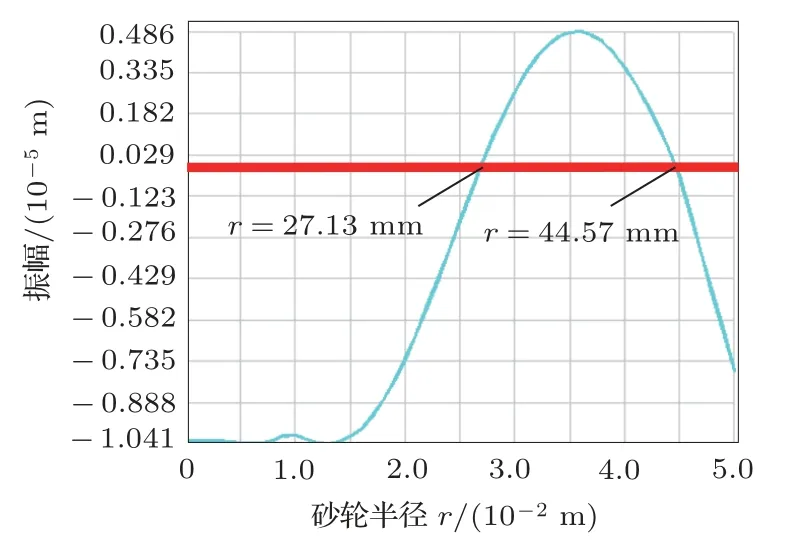
图6 平行砂轮谐响应分析振幅曲线Fig.6 Harmonic analysis of parallel grinding wheel

4 复合变幅器的谐振特性试验

4.1 阻抗特性测试试验

通过上述的有限元仿真分析验证了设计的可行性，依据表2的复合变幅器尺寸参数进行变幅器各部分零件的加工，并将其组成了谐振系统，使用PV70A型阻抗分析仪进行了阻抗分析试验，具体的阻抗测试装置如图7所示，得到的测量结果如图8所示。

图7 阻抗分析试验Fig.7 Impedance analysitest

通过得到的阻抗测试结果分析得到，该谐振系统的导纳曲线为一个完整的单圆，对数坐标系中的阻抗曲线仅可得到一对极小值和极大值，相位角曲线呈现明显的“几”字形，这表明换能器与复合变幅杆在连接面处接触状况良好，所施加预紧力合适。且超声振动系统机械品质因数较好，表明声电转化率高。由此证明本设计的复合变幅杆结构和尺寸较合理。在图8的参数栏中，该谐振系统的谐振频率为28495 Hz，误差为1.77%，这说明该超声振动系统的工作频率与换能器本身的工作频率相差很小，谐振系统可以处于一个比较理想的工作状态。

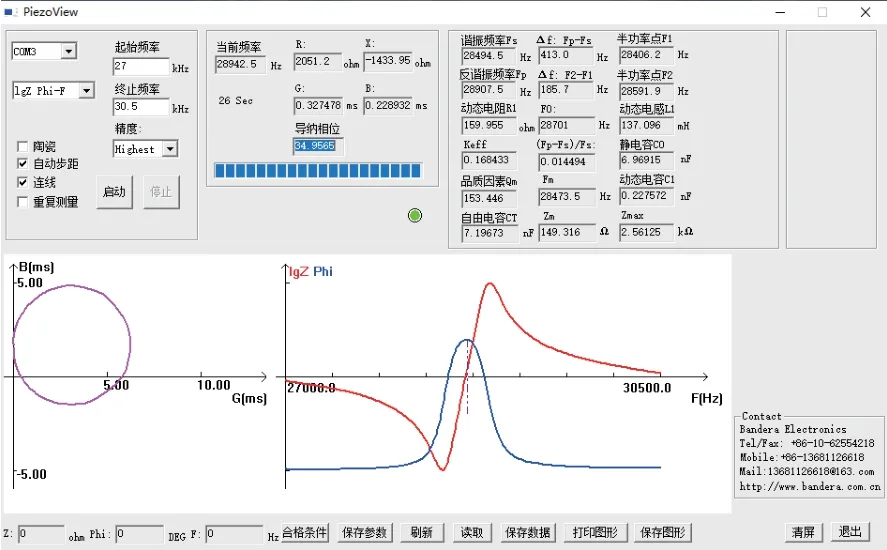
图8 阻抗测试结果Fig.8 Result of impedance analysis test

4.2 谐振试验分析

为了研究该谐振系统的谐振特性，将谐振系统与导电滑环和刀柄套筒进行装配得到了如图9所示的超声刀具系统，并通过超声谐振试验为进行超声磨削试验做准备。将超声波电源、谐振系统、示波器等试验设备连接完毕后，启动超声波电源，通过调频螺母使得超声波电源正常工作，整个谐振系统振动的声音较小且没有异响，利用示波器测得谐振系统的谐振频率约为28889 Hz，表明该谐振系统稳定工作。

图9 超声谐振试验装置Fig.9 Ultrasonic resonance test setup

为了测量谐振系统表面的节圆的具体位置，在砂轮表面均匀撒上碳化硅砂粒，开启超声波电源后，碳化硅砂粒在高频振动的作用下形成为两个节圆环，如图10所示，表明平行砂轮在做节圆型弯曲振动，与理论设计中的弯曲振动假设和有限元仿真分析结果相符。

图10 超声谐振试验结果Fig.10 Result of ultrasonic resonance test

对超声谐振系统得到的如图10所示两节圆的位置进行测量，得到两节圆的半径分别为r1= 27.33 mm、r2= 44.17 mm，并通过理论计算和有限元分析软件进行谐响应分析得到的节圆半径结果如表3所示，并得到仿真误差∆U1= [|理论半径−仿真半径|/理论半径]、试验误差∆U2=[|理论半径−试验半径|/理论半径]。经计算仿真误差∆U1均小于4%、试验误差∆U2均小于5%。通过超声谐振试验证明所研制的平行砂轮超声磨削主轴附件式刀具系统谐振效果较好，为进行超声加工试验奠定了基础。