基于Gammatone滤波器组时频谱和卷积神经网络的海底底质分类∗
2021-09-22逄岩许枫刘佳
逄 岩 许 枫 刘 佳
(1 中国科学院声学研究所 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
利用采样工具进行站点式取样底质数据完成海底底质的探测与分类虽然准确直观,却存在着效率低以及不适合大规模调查等缺点[1]。底质数据的获取是完成底质分类的基础,通过侧扫声呐获取底质数据具有操作简单、覆盖面积广以及分辨率高等优点。目前利用侧扫声呐获取底质数据进行底质分类主要有两种研究思路:一是提取海底底质的侧扫声呐图像纹理等特征完成底质分类[2−3];二是校正获取的侧扫声呐数据得到只与底质类型有关的散射强度数据,提取有效分类特征实现底质分类[4−5]。
模拟耳蜗听觉模型的Gammatone 滤波器组(Gammatone filter banks,GFB)具有较高语声识别准确率和抗噪能力,能够有效分析非平稳信号,描述信号的瞬间变化[6−7]。由于底质存在凹凸不平等非均匀性特征,声波会在底质表面发生随机散射,从而导致底质反向散射的声波信号具有非平稳性以及瞬变特性,因此Gammatone 滤波器组可以用于分析底质反向散射信号。近年来,以卷积神经网络(Convolutional neural networks,CNN)为主的深度学习方法在目标检测[8]、人脸识别[9]以及文本分类[10]等领域得到广泛应用,将CNN 方法应用到海底底质分类逐步成为一种研究趋势。Berthold等[11]通过GoogLeNet 对砾石、泥、沙和混合底质4 种底质进行初步分类;Luo 等[12]利用深层和浅层CNN 模型对石、泥和沙3 种底质进行分类比较,在取得优秀的分类表现的同时发现浅层CNN 模型的分类性能优于深层CNN 模型。上述研究验证了CNN 方法在底质分类中的可行性以及有效性,为CNN方法在底质分类中的深入研究奠定了基础。
本文将CNN 方法与底质信号分析相结合,利用构造的CNN 模型学习Gammatone 滤波器组分析计算的底质信号时频谱进行底质的分类识别,最终取得良好的分类效果。
1 Gammatone滤波器
Gammatone滤波器(Gammatone filter,GTF)是一种近似于Revcor函数的解析数学函数,在保留完整的幅度信息的同时还兼备完整的相位信息[13]。
1.1 Gammatone滤波器组
Gammatone 滤波器组[14]最早用于描述听觉系统脉冲响应,是一个标准的耳蜗听觉线性滤波器组,其时域表达式为

其中,c为滤波器增益,m为滤波器阶数,fi为第i个滤波器的中心频率;ϕi为第i个滤波器的初始相位,由于初始相位对听觉系统影响较小,同时为简化滤波器组模型,所有ϕi取为0;N为Gammatone 滤波器的个数;bi为第i个滤波器的衰减因子,与对应滤波器等效矩形带宽ERB(fi)有关,同时决定脉冲响应的衰减速度,其中,bi= 1.019ERB(fi),ERB(fi)如式(2)所示:
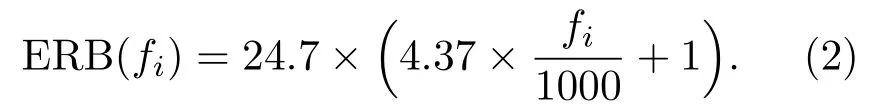
各个滤波器的中心频率在ERB 域上等间隔分布。滤波器个数为64,中心频率范围为50~128 Hz 时Gammatone 滤波器组的幅频响应如图1(a)所示,不同通道数时各通道中心频率在ERB 域的变化如图1(b)所示,不同中心频率时Gammatone 滤波器时域波形如图1(c)所示。
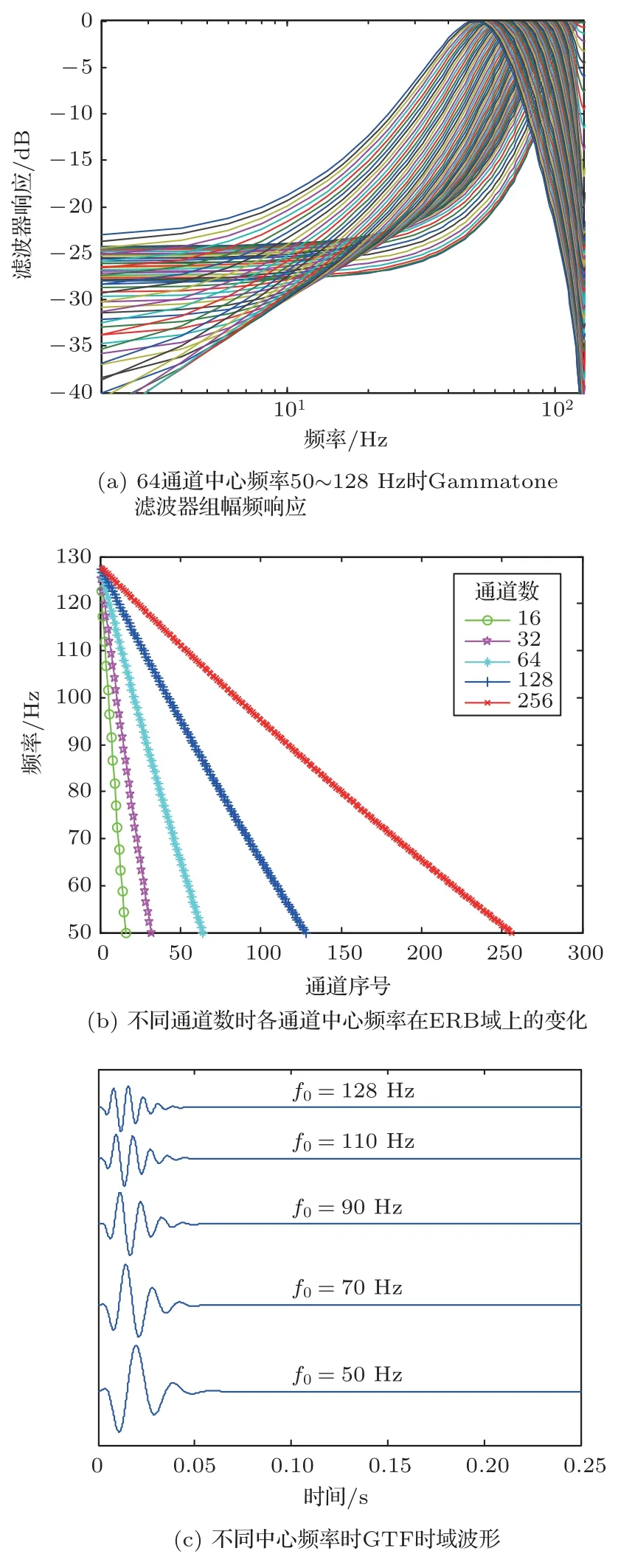
图1 GFB 不同通道数和中心频率时的波形变化Fig.1 GFB waveforms in different channel numbers and center frequencies
1.2 Gammatone滤波器组时频谱
时频分析是将信号时域和频域相结合分析信号的时频联合特征,克服只能在时域或频域分析信号的缺点。传统的时频分析方法包含短时傅里叶变换(Short time Fourier transform,STFT)、小波变换以及Wigner-Ville 分布等。但STFT 的分析结果易受窗函数的影响,同时窗口大小的设置难以确定;小波变换存在小波基选择的难点;Wigner-Ville 分布虽然具有良好的时频聚焦特性,但同时容易产生交叉项的干扰[15−16]。由于底质信号的非平稳性和瞬变特性以及GFB 在分析上述特性具有显著优势,同时GFB很好地模拟了耳蜗基底膜,兼具良好的频率选择特性和频谱分析特性,能够对底质信号低频部分保持较高频率分辨率,同时对底质信号高频部分信号保持较高的时间分辨率。因此利用GFB 在能够对底质信号实现更为精细化时频分析的同时,在分析过程中也避免产生交叉项的干扰。
由图2所示,本文设计的底质信号GFB 时频谱计算步骤如下:
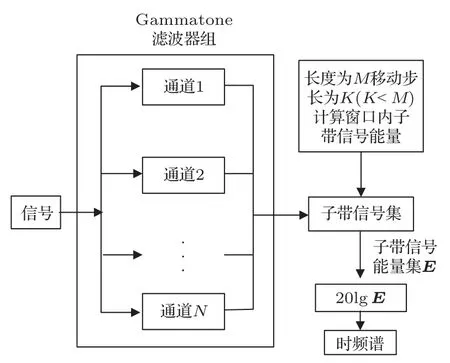
图2 GFB 时频谱计算流程Fig.2 GFB time-frequency spectrum calculation processs
(1)利用GFB 对原始底质信号进行滤波后得到一组数目与GFB通道数目相同的子带信号;
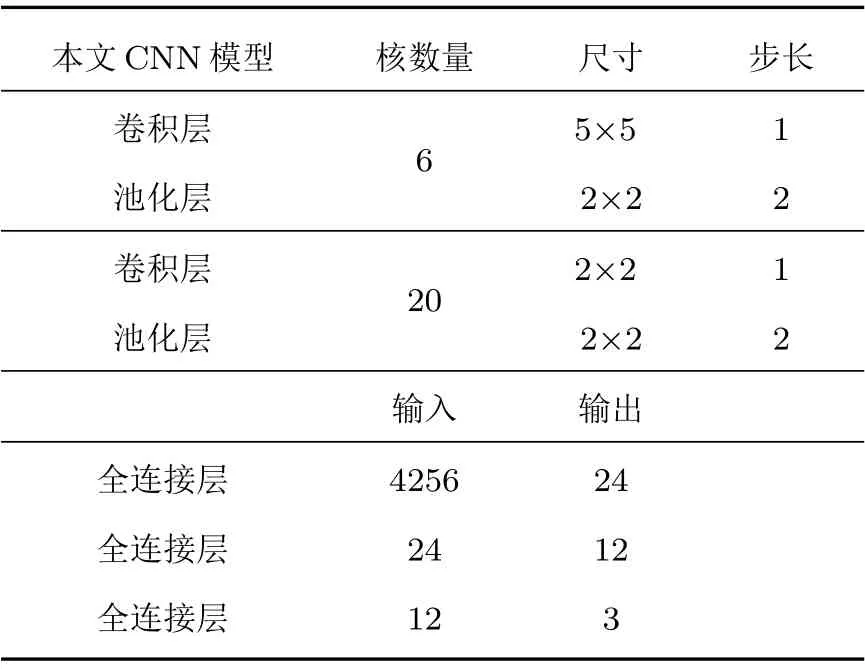
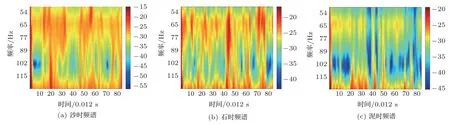
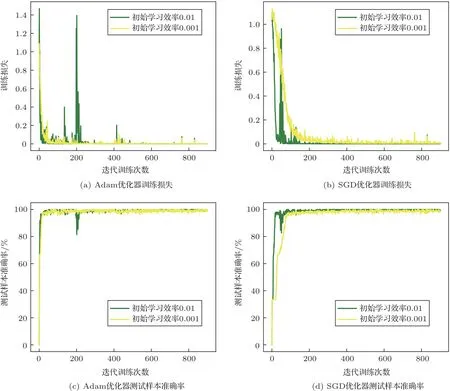
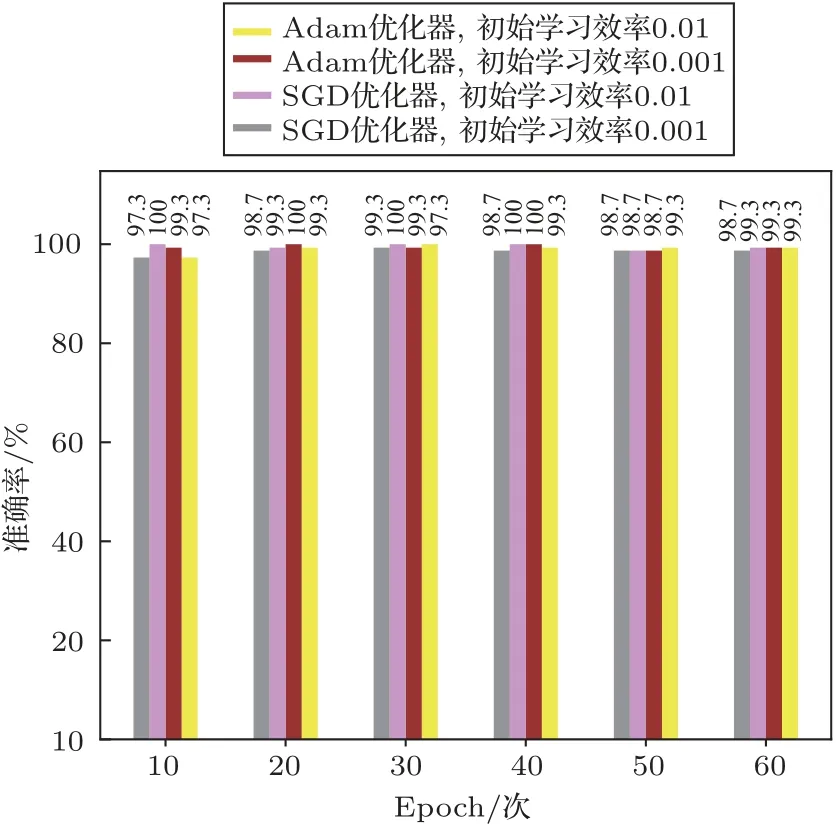
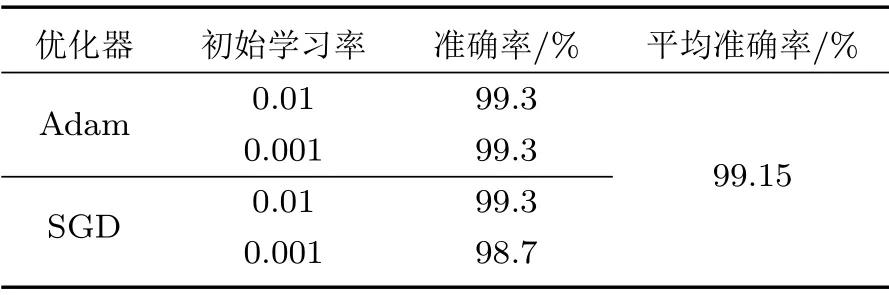
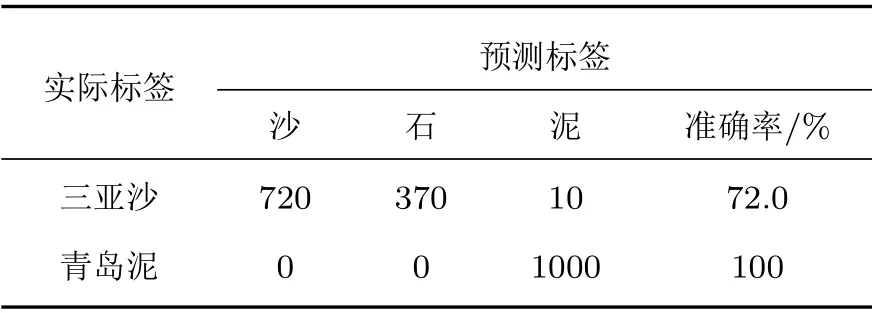
(2)取长度为M的窗口在每一条子带信号上以步长为K(K (3)对步骤(2)中计算所得到的所有子带信号能量集E进行对数运算,得到原始底质信号的GFB时频谱。 CNN[17]是一种主要包含卷积层(含激励操作)、池化层和全连接层的深度学习结构,通过卷积、激活和池化操作自动学习提取图像特征后利用全连接层输出分类结果达到最终的分类目的。 卷积层主要是由若干个卷积核组成,通过卷积操作能够提取输入信息的不同层次特征,随着卷积层深度的增加,CNN 越注重提取更深层次的特征,最后卷积结果通过激励层得到特征图。所有卷积层通过BP 算法进行权重更新进而实现整个CNN 模型的优化,卷积层操作表达式如下: 其中,xln为卷积层l第n个通道的输出,Pn为卷积层l的输入特征图集(卷积层l−1的输出特征图集),为第l −1 卷积层的输出特征图,为卷积核权重矩阵,bln为偏置。f(·)为激励函数,本质上是对卷积层输出进行一次非线性映射[18],增加整个CNN 模型的非线性特性,常用的激励函数有ReLU函数、sigmoid 函数、tanh 函数以及softplus 函数,4种激励函数图像如图3所示。 图3 4 种激励函数Fig.3 Four kinds of activation function 相对于利用分类器分类人工提取的底质分类特征实现底质的分类,CNN方法将底质数据特征提取与分类两个过程融为整体,利用自身网络结构中的多个卷积核自下而上、由浅入深提取学习底质数据的特征,独立得到底质数据全面综合的特征信息后利用全连接层完成底质分类。在解决人工选取有效分类特征难点的同时通过自身模型的训练优化自动得到最有效的分类特征,进而达到底质识别分类的目的。 LeNet-5[19]卷积神经网络是Yann LeCun 于1998年提出用于手写体数字识别的CNN,其网络结构如图4所示。该CNN 模型包含2 个卷积层、2 个池化层、2 个全连接层以及1 个softmax 输出层,通过卷积、参数共享以及池化等操作对手写体数字取得了优秀的识别率。 图4 LeNet-5 卷积神经网络结构示意图[19]Fig.4 The schematic diagram of LeNet-5 CNN[19] 在本文中,以LeNet-5卷积神经网络为基础,构造包含2 个卷积层、2 个池化层和3 个全连接层共7层网络层的CNN 模型。第一个卷积层的卷积核数量为6,核大小设置为5×5,进行卷积操作时的步长为1;第二个卷积层的卷积核数量增加到20,同时核大小减小为2×2,但卷积操作的卷积步长仍然保持不变为1。同时在2 个卷积层各带有1 个池化层,池化核的大小均为2×2,统一设置池化步长为2,同时2 个池化层的池化方式均采用最大采样。最后的3 个全连接层将输入特征进行特征映射实现最后的底质分类目的。最终的CNN模型结构如表1所示。 表1 本文所采用的CNN 模型结构Table 1 The CNN model structure used in this paper 在本次实验中,采用了美国加州州立大学海底测绘实验室(SFML)在加利福尼亚州Scott Creek近海所采集的侧扫声呐图像数据,采集记录底质类型主要为沙、石和泥。由于底质的侧扫声呐图像在成图前已经经过系统误差校正以及Lambert 校正,因此可以从图像中提取一维数据作为底质信号。从沙、石和泥3 种底质图像中分别提取300 条长度为256点的一维数据作为底质信号数据,3组底质数据中各随机抽取250 条数据作为训练样本,剩余数据作为测试样本,训练样本与测试样本的比例为5:1。 由于实验数据是从底质图像中提取,假设每段数据是在1 s 的时间内采集,数据采样率为256 Hz,最终前文所述的Gammatone 滤波器参数中增益c设为1,阶数m设为4,滤波器个数设为64,中心频率范围为50~128 Hz。同时根据GFB 实际输入数据长度将M设为6,K设为2。沙、石和泥经过GFB时频分析得到的时频谱(大小为64×84)如图5所示,其中图5(a)、图5(b)、图5(c)分别为沙、石和泥信号GFB时频谱。 图5 沙、石和泥的GFB 时频谱Fig.5 The GFB time-frequency sperctrum of sand,rock and mud 在本文中,样本训练采用批次训练,批次大小为50,每当全部数据训练30 次后,学习率会以0.1倍数下降,损失函数采用交叉熵损失函数(Crossentropy error function),具体实验流程如图6所示。 图6 实验流程Fig.6 Experiment process 为了充分验证利用构建的CNN 模型分类底质图像信号GFB 时频谱所达到的底质分类效果,在实验中分别利用随机梯度下降(Stochastic gradient descent,SGD)优化器和Adam优化器对CNN 模型进行优化,同时对分类结果进行比较分析。此外,通过设置初始学习率为0.01 和0.001 验证上述优化器在不同学习率条件下的学习和分类能力。两种优化器在不同初始学习率下训练损失与测试准确率变化过程和测试准确率随训练次数变化结果分别如图7和图8所示。 图7 两种优化器不同初始学习率下训练损失与测试准确率对比Fig.7 Comparison of training loss and test accuracy of two optimizers with different initial learning rates 图8 两种优化器不同初始学习率在不同训练次数时的测试准确率Fig.8 The accuracy of the two optimizers with different initial learning rates at different training times 通过实验结果可知,采用Adam优化器,初始学习率为0.01 时,训练损失和测试准确率虽然在训练过程中发生明显起伏,但在训练样本训练10次以后达到收敛;初始学习率为0.001 时,训练损失和测试准确率在全部样本训练10次后同样达到收敛,同时二者变化相对理想平稳;两种初始学习率条件下的测试准确率最终逐步稳定在99%左右。采用SGD优化器,初始学习率0.01 时,训练损失和测试准确率变化情况与Adam 优化器时的变化情况类似;而初始学习率为0.001 时,训练损失和测试准确率收敛速度相对较慢,但在训练过程中训练损失和测试准确率变化平稳,两种初始学习率条件下的测试准确率最终也逐步稳定在99%左右。总体而言,本文提出的方法取得了较高的分类准确率,整体分类结果如表2所示。 表2 本文方法在不同初始学习率下的分类结果Table 2 Classification results of this method under different initial learning rates 为了验证本文方法有效性,选取底质信号分类领域一些较为常见的方法进行比较,进行分类准确率对比。本文所采用方法的平均分类准确率达到99.15%,均高于其他方法(表3)。 表3 本文方法与其他方法比较Table 3 Comparison of the method in this paper with other methods 相同底质的信号时频分析结果在局部细节和全局分布上具有较大的相似性,同时通过底质时频分析数据训练后的CNN 模型获得了对数据局部细节和全局分布关注力度不同的卷积权重。当CNN模型对训练集和测试集以外的数据进行分类识别时,会利用卷积权重着重聚焦新输入数据的区域重点和全局趋势,利用新输入数据提取的综合特征信息完成分类,因此本文方法会具有一定的泛化能力。为了验证本文所提出方法的泛化能力,利用青岛某海域和三亚某海域采集到的底质侧扫声呐图像数据。其中,青岛底质主要为泥,三亚底质主要为沙,分别从底质图像中各提取1000 段长度为256 点的数据进行测试,最终的测试结果如表4所示。 表4 本文方法泛化能力验证结果Table 4 Test results of generalization ability of this method 表4实验结果表明,本文方法对于泥底质已经取得优异的分类效果,能够达到分类目的;而对于沙底质和石底质,由于该两种底质在物理特性上具有较大的相似性,分类效果并不是很理想。针对这一问题,可以增加CNN模型层数,进一步提高CNN模型对底质数据更深层次特征的学习能力,或者在训练数据增加其他地方的沙底质和石底质数据样本,提高本文方法对沙底质和石底质的泛化能力。最后,为了验证上述方法对本文方法泛化能力的改进情况,采用增加数据样本的方式,对3类底质计算得到的GFB时频谱进行水平、垂直和水平垂直镜像操作后,将训练集合测试集扩充为原始数据的4 倍。利用扩充后数据对搭建的模型进行训练后,再次利用上述青岛沙和三亚泥数据集进行测试,改进结果如表5所示。 表5 改进后泛化能力验证结果Table 5 The verification results of generalization ability after improvement 表5的改进结果证明通过增加训练数据的数量可以提升本文方法的泛化能力,也为进一步提高泛化能力的深入研究提供了思路方向,最终实现在提高本文方法泛化能力的同时达到准确分类底质的目的。 本文将深度学习的思想应用到海底底质分类当中,将底质图像信号的Gammatone 滤波器组时频谱作为CNN 模型的输入,进行底质的分类识别,取得了较高的分类准确率,分类准确率均优于其他常用底质分类的方法。同时,本文进一步验证了所提出的方法对于泥底质具有很好的泛化能力,但对于沙底质和泥底质,泛化能力不强,需要通过增加CNN 模型层数或者增加沙和石底质训练样本数量来进一步完善本文提出的方法。此外,本文采用的底质信号数据集均提取于底质的侧扫声呐图像,未来有待进一步使用原始的底质侧扫数据进行研究论证,以实现在实际中的应用。2 CNN
2.1 CNN介绍
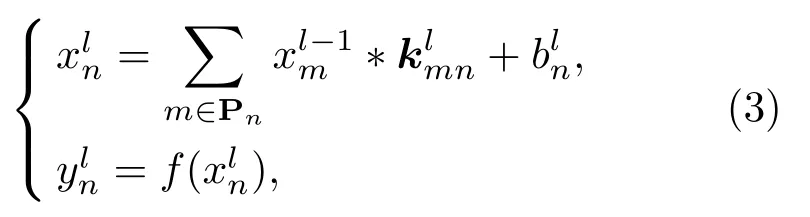
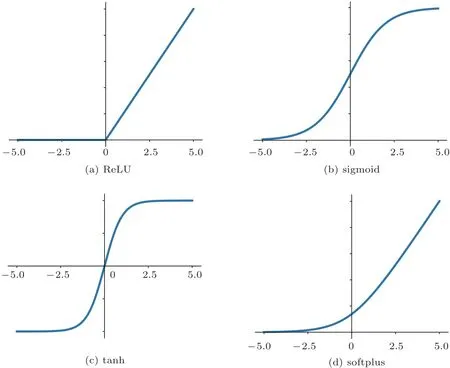
2.2 本文所构建的CNN模型

3 实验过程及分析
3.1 实验数据与实验过程

3.2 实验结果与分析


4 结论
