含周期性空腔结构吸声机理的研究∗

罗英勤 楼京俊 张焱冰 李静茹

(1 海军工程大学舰船与海洋学院 武汉 430000)

(2 海南大学机电工程学院 海口 570100)

0 引言

含空腔的吸声结构已经被证明是很有效的吸声结构，分析和计算其吸声机理和吸声系数的方法主要有理论计算方法如解析法[1−3]、传递矩阵法[4−6]、等效参数法[7−8]、多重散射法[9−12]等。但理论计算方法一般只适用于结构形式比较简单的吸声结构；数值仿真方法在处理复杂结构上具有灵活通用性，能直观展示结构在声波激励下的变形、能量消散图像。Hoennion等[13−14]首次将有限元(Finite element method,FEM)理论与Bloch-Floquet理论相结合，研究了柔顺管和Alberich 消声涂层的散射。Achenbach 等[15]利用边界元法研究了由平行等距杆组成的格栅对平面声波的三维反射和透射。Easwaran等[16]提出了一种基于Galerkin函数的有限元方案，用于分析垂直入射平面声波穿过时共振吸收器的反射特性。此后数值仿真越来越普遍地应用于声学仿真[17−20]。数值仿真实质上是对结构和声学介质的离散化处理，为保证计算精度，相应的模型网格取1/4 最小波长[14]，在处理高频问题时，波长更小，使得计算量大大增加，特别是在多次重复计算的优化问题中，此问题尤为突出，此时可以根据结构的对称特性简化为1/4[16]或1/8 模型[11]甚至是二维轴对称模型[18]，相应的计算效率和计算精度有待进一步验证。本文在利用有限元仿真软件建立声学性能分析方法的基础上，提出并验证了含轴对称空腔周期性吸声结构计算的简化方法。

含空腔吸声结构的吸声机理一直备受关注。Gaunaurd[21]认为这种含空腔结构的声特性与第二层圆柱孔的谐振有关。后来Lane[22]发现其声特性不仅与第二层空腔有关还与第一层的动态特性有关。Gaunaurd[23]在对文献[22]的评论中指出，空腔结构第一层的弯曲振动、第二层孔壁的径向运动，是两种振动机理共同作用。文献[20]指出吸声机理包括第一层的“隔膜”共振和第二层的孔壁的径向运动，起主要作用的机理不仅与各层的刚度匹配有关，还与孔的大小和各层厚度有关。近年来，Ivansson在讨论周期性分布的球型空腔和椭球型空腔[18]吸声结构的声学性能时考虑了腔的多重散射特性。白国锋等[24]总结以上吸声机理为空腔发生共振增加能量损耗；空腔增加波的散射以及增加波的传播路径；空腔径向运动增加波型转化，利用横波衰减因子提高声能吸收。

本文对水下环境中的含圆柱空腔吸声结构进行了优化设计，并对声能量损耗机理进行了分析。观察到空腔运动不仅是表面层的弯曲振动和空腔附近的径向运动，而且径向运动随吸声结构厚度变化。相对以往相关内容文献，本文还比较详细地介绍了结构模型简化过程和计算效率、计算精度提升的效果，为进一步揭示空腔吸声机理的细节提供了理论依据。

1 吸声特性计算简化模型及验证

1.1 模型描述

采用有限元方法建立声固耦合方程如下[17]：

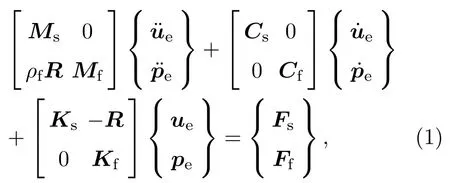
其中，M、C、K、R分别是质量、阻尼、刚度矩阵以及结构和流体的耦合矩阵，下标s 和f 分别表示结构和流体，ue和pe分别是结构节点位移和流体的节点声压，Fs和Ff分别表示结构受力和声压激励，ρf表示流体密度。以此为基础建立有限元仿真模型，流体介质两端分别施加完全匹配层(Perfectly matched layer,PML)形成吸声端面。经求解得到反射系数R和透射系数T，由公式(2)求得吸声系数：

二维周期结构是指沿xOy平面排布的四边形和六边形，截面单元如图1所示，本文主要分析这种周期分布的吸声结构。实际分析过程只需取一个单元，对单元模型外表面施加周期性边界条件un=0。根据结构对称性，可以取四边形截面单元的1/4(如图1(a)黄色部分)甚至1/8(如图1(a)红色部分)或者六边形截面单元的1/4(如图1(b)黄色部分)或1/6(如图1(b)红色部分)进行仿真。对于含轴对称空腔的周期结构，保持空腔尺寸不变，利用通孔率ϕ相等将四边形或六边形截面的单元转化为圆形截面单元，可进一步简化采用二维轴对称模型进行计算，以四边形截面单元为例，简化过程如图2所示。

图1 平面周期单元形式Fig.1 Plane periodic unit form

图2 含轴对称空腔周期结构分析模型简化过程图Fig.2 Simplified process diagram of periodic structure analysis model with axisymmetric cavity

1.2 模型验证

算例1 以一个多层吸声结构为例，各层材料参数和厚度如表1所示，流体介质密度ρ=1.12 kg/m³，声速c= 340 m/s，钢被衬。其中第二层含有周期性空腔通孔，空腔直径d为10 mm，空腔间距s为30 mm，计算频率为50～500 Hz，步长为10 Hz。

表1 含空腔结构几何和材料参数Table 1 The geometry and material parameters of the structure containing cavity

取一个正方形截面单元进行分析，取单元立方体、1/4 立方体、通孔率相同的圆柱立方体、通孔率相同的二维轴对称模型建立简化模型，计算声学性能。各简化模型的计算结果曲线如图3所示，计算量、计算时间和平均误差如表2所示，可知二维轴对称模型的简化方法误差不到1%，满足精度需求且计算效率大大提高，可以在结构优化计算过程中节约大量时间，缩短设计周期。

图3 算例1 吸声系数计算结果Fig.3 Calculation results of sound absorption coefficient of Example 1

表2 简化模型计算对比结果Table 2 Calculation results of simplified model

2 含周期圆柱空腔吸声结构优化设计

采用遗传算法对吸声结构进行优化设计，遗传算法[25]利用适应度函数将目标函数转化为对应变量的适应度。将变量编码作为基因形成染色体个体，通过染色体基因的变换和重组完成“杂交”、“变异”的过程，用适应度函数对染色体个体进行评价，模拟自然界中的“优胜劣汰”、“适者生存”，最终完成寻优搜索的过程。遗传算法兼顾全局和局部搜索能力，优化流程如图4所示。

图4 遗传算法流程图Fig.4 Flowchart of genetic algorithm

针对水下结构有限厚度低频吸声问题，设计水被衬含圆柱空腔吸声结构，水介质参数为ρ= 1000 kg/m3，c= 1500 m/s。各层材料之间的刚度匹配和空腔形状影响吸声性能，这里仅对空腔形状和各层厚度进行优化设计。各层均采用聚氨酯材料，材料参数为E= 35.17 MPa，v= 0.45，ρ=950 kg/m3，η=0.43。吸声结构如图5所示，在2000 Hz 频率下用遗传算法对圆柱空腔吸声性能进行优化设计。此处采用遗传算法ga 函数链接有限元仿真软件进行优化设计，ga 函数是求解目标函数的最小值，此处目标函数是求吸声系数α的最大值，对应优化模型如下：

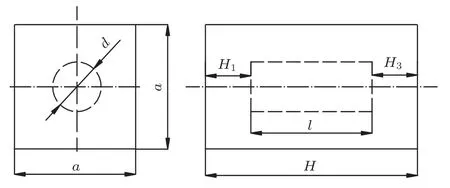
图5 含空腔结构示意图Fig.5 Structure diagram with cavity

其中设计参数单位为mm，优化结果如表3所示，优化前后1000～3000 Hz 频率下声学性能曲线如图6所示，吸声系数在大部分频段提高。

表3 圆柱空腔吸声结构优化设计参数设置及结果Table 3 Parameter setting and results of optimization design

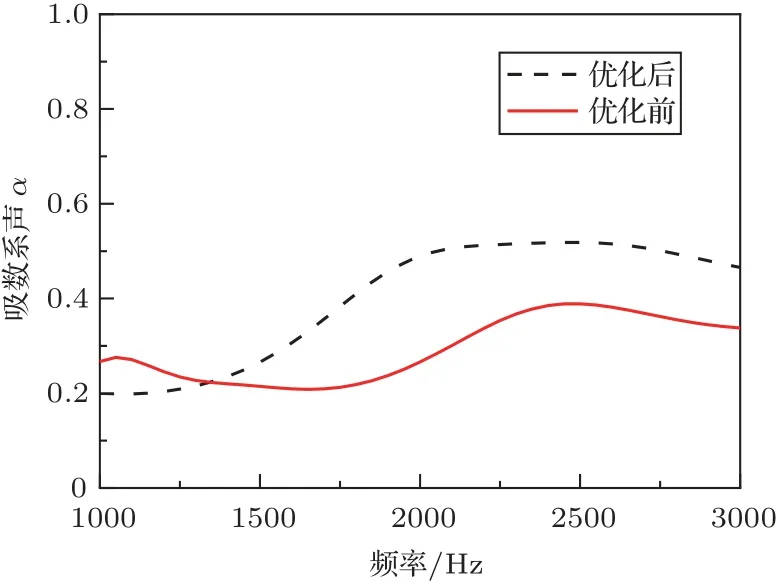
图6 含圆柱空腔结构吸声系数优化结果Fig.6 Optimization result of sound absorption coefficient of structure with cylindrical cavity

2.1 能耗分析

实现吸声的实质是将声能转化为热能等其他形式耗散掉，所以能量耗散多少直接关系到吸声系数的大小，借助有限元仿真提取能量耗散密度来分析空腔结构吸声机理。图7给出了优化前后表层和空腔层的能量消耗随频率变化情况，图8给出了优化后对称截面能耗密度分布情况。优化前低于1400 Hz 频率区表层能耗高于空腔层的能耗，高于1400 Hz 频率区空腔层的能耗高于表层能耗；优化后在整个频段内，空腔层的能耗明显大于表层能耗，且相比于优化前，优化后空腔层能耗高于表层能耗的程度加大。虽然图8显示表层能量密度高于空腔层的，但是空腔层体积更大，总能耗大。由此表明，空腔层的吸声作用起主导，结构会朝着增加空腔层能耗的方向优化。因为2500 Hz 下吸声系数比目标频率2000 Hz下更高，图8展示了2500 Hz下能耗密度分布，相比于2000 Hz 情况，其空腔附近能耗密度明显增大，这与图9(b)、图9(d)发生明显径向变形有关。

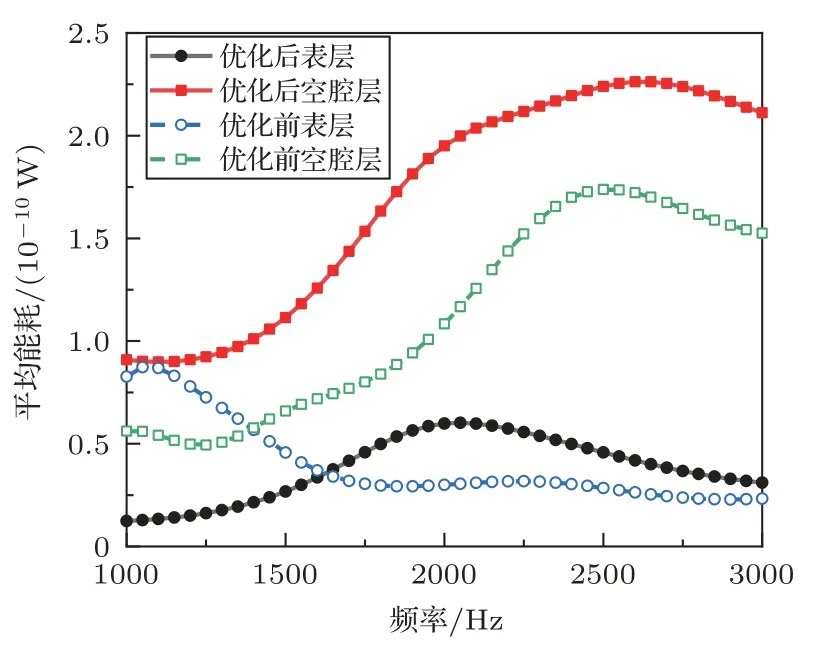
图7 优化前后空腔结构各层平均功耗Fig.7 Average power consumption of each layer of cavity structure before and after optimization

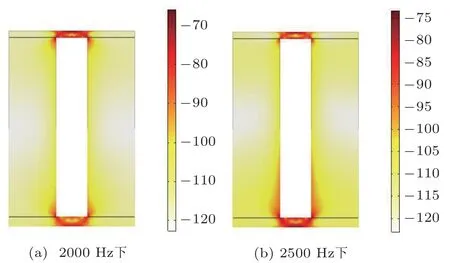
图8 圆柱空腔结构能耗分布Fig.8 Energy consumption distribution of cylindrical cavity structure

2.2 变形分析

图9给出了优化后结构变形，图中黑实线表示未变形结构，箭头表示质点位移矢量，箭头方向表示位移方向，箭头相对大小表示位移相对大小。由图9(a)和图9(c)可以看出，在2000 Hz 频率下空腔上下表层发生明显的弯曲变形，由图9(c)、图9(e)和图9(g)看出，空腔层发生径向变形，没有扭转变形，且上半部分从空腔向外膨胀，下半部分向空腔内收缩，从变形数量级上可知径向位移比表层位移小一个数量级，几乎可以忽略。因为图6显示2500 Hz 下吸声系数比目标频率2000 Hz 下更高，图9展示了2500 Hz 下结构变形，入射侧表层结构依然明显弯曲，但图9(b)、图9(d)相比于图9(a)、图9(c)，空腔层发生了明显的径向变形，且径向变形轴向变化，表明径向运动对吸声性能影响很大。

图9 圆柱空腔变形Fig.9 Deformation of cylindrical cavity structure

2.3 模态分析

图10给出了优化后圆柱空腔结构的前3 阶模态，第1 阶主要发生表层变形，第2 阶同样主要发生表层变形，但是径向变形相对第1 阶增大，第3 阶产生表层变形的同时也产生了比较明显径向变形模态。2000 Hz 下主要激起第1 阶模态，如图10所示，第1 阶模态与图9(c)变形对应。2500 Hz 可以激起前3 阶模态，其变形由前3 阶模态叠加，第3 阶频率为2426.8 Hz，叠加成分最高，发生更多的径向变形，对应2500 Hz 吸声系数高于2000 Hz。对优化后结构的能量消耗、变形和模态分析表明，低频段吸声性能主要与表层变形有关，激起表层振动模态，进而激起表层结构介质运动而消耗能量，相对而言高频段可激发结构的径向变形模态，激起更多的吸声结构介质运动而消耗能量，所以径向变形对提高吸声系数作用很大。

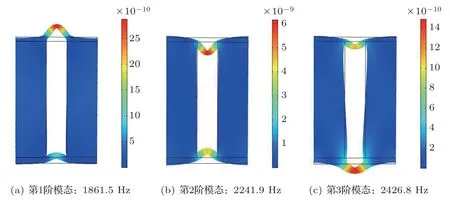
图10 优化后圆柱空腔前3 阶模态Fig.10 The first 3 modes of the cylindrical cavity after optimization

3 结论

针对周期单元满足轴对称的吸声结构提出二维轴对称模型简化方法，通过对比计算验证了简化方法满足精度需求且大大提高计算效率。

在水下环境，用二维轴对称模型结合遗传算法对含周期性圆柱空腔结构的吸声性能在频率2000 Hz 下进行了优化设计，计算优化后结构在1 kHz～3 kHz 频段声学性能可知，吸声系数在2500 Hz达到最大。经过分析主要得到以下结论：

(1)径向运动促进纵波转化为损耗因子较大的横波，从而提升了声波能量的损耗，径向振动程度对能量耗散影响很大。

(2)空腔谐振包括表层的弯曲振动和空腔附近的径向变形，频率相对高时发生更明显的径向运动，且径向运动随吸声结构厚度变化；频率相对低时表层弯曲运动发挥主要作用；频率相对高时径向运动对吸声性能影响更大。

(3)激发径向运动模态有助于提高吸声系数。由此思路启发，考虑到变截面空腔径向运动模态更丰富，更有助于径向模态向低频移动，变截面空腔设计为提高低频段吸声系数提供了更多可能。