表征超声衰减谱粒度的改进和声搜索算法∗

蒋 瑜 曲佩玙 贾 楠 苏明旭

(上海理工大学 动力工程多相流与传热重点实验室 上海 200093)

0 引言

颗粒物广泛存在于各个领域，能源领域水煤浆高效燃烧，食品行业食品结晶、均质化，医药行业药物粒径大小及其在生物体内运输等都涉及到颗粒表征技术[1−4]。典型颗粒测量技术有沉降法[5]、显微镜法[6]、动态光散射法[7]、超声衰减谱法等，其中超声衰减谱法具有非侵入性、样品无需稀释、装置成本低等优点。超声波在介质中传播产生衰减，携带粒径信息，因此通过实验获得超声衰减谱，结合McClements 模型[8]、Epstein-Carhart-Allegra-Hawley(ECAH)模型[9−10]，可进一步反演得到颗粒粒径分布。

反演算法可分为独立模式和非独立模式两类，独立模式无需预设分布，求解离散方程组得到粒径分布；非独立模式通常假定颗粒服从高斯分布、罗辛-拉姆勒(Rosin-Rammler,R-R)分布或对数正态分布，然后定义理论预测与实测衰减谱的误差作为目标函数来构建优化问题，求取最佳粒径分布。人工智能算法的迅速发展，为推动此类方法提供了巨大的发展潜力。目前非独立模式下粒径反演中人工鱼群算法(Artificial fish school algorithm,AFSA)[11]、蚁群算法(Ant colony optimization algorithm,ACO)[12]和遗传算法(Genetic algorithm,GA)[13]等得到了较好的研究。与前述算法相比，和声搜索算法(Harmony search algorithm,HS)作为一种启发式全局搜索算法[14]，具有结构简单、全局搜索能力强等优点。欧阳海滨等[15]研究和声搜索算法和反向学习策略，提出反向学习产生新和声与之前的和声进行末位淘汰竞争机制，并应用于优化热交换器和减速器设计问题；Alireza 等[16]利用和声搜索算法优化配电网络中配电机组配置，以降低系统功耗、改善系统电压分布、提高电压稳定性；Hussein 等[17]利用和声搜索算法和主成分分析相结合(Hybrid principal component analysis,HPCA)，利用HPCA 加快对图像处理；Shams等[18]将和声搜索算法应用油藏工程历史匹配问题；陈涛[19]针对特征基因选择问题提出用概率决定对最差和声或最好和声进行变异来优化和声搜索算法。上述在一定程度上提升了算法的性能，但是未能解决算法容易陷入局部最优解、求解精度不高的问题。

为此，提出一种超声衰减非独立模式反演的改进，其核心为通过和声搜索算法与拟牛顿法(Broyden-Fletcher-Goldfarb-Shanno,BFGS)[20]并行计算，合理调节和取舍全局搜索与局部搜索能力，使算法兼顾全局搜索效率和逼近精度。针对R-R分布、正态分布、对数正态分布函数的多种粒径分布情况进行模拟，并通过实验超声衰减谱法的反演和图像法结果对比分析，充分验证了改进算法的有效性、抗噪性。

1 目标函数构建

当超声波通过含颗粒物介质时，由于颗粒与声波的作用而产生衰减，可从理论上较为全面地考虑声波和颗粒相互作用的多种机制，多分散颗粒系中声衰减系数α表达式为

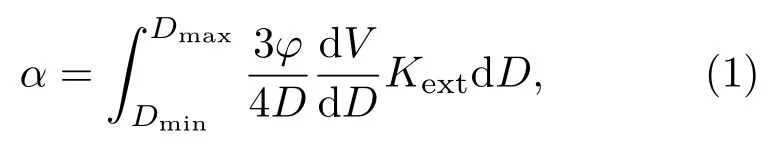
其中，Kext是模型定义的消声系数，dV/dD是颗粒体积频度分布，为待求值。式(1)在数学上属第一类Fredholm 积分方程，该方程目前没有理论解析解，将式(1)离散，可写成矩阵形式：

其中，G为声衰减分布列向量，A为衰减系数矩阵，向量W为被测颗粒的粒径分布。式(2)是典型的病态方程，常采用最优化算法求解。

在非独立求解模式下，通常颗粒系被描述为粒径频度分布服从一定的函数形式，例如正态分布、对数正态分布或R-R分布，后者由式(3)给出：

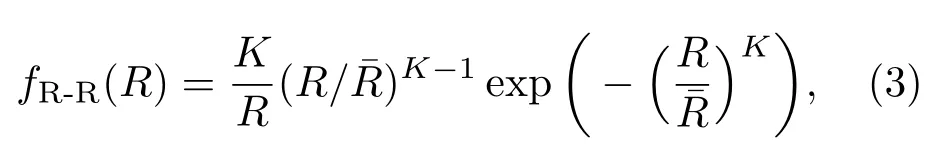
为便于采用最优化理论求解，往往依据超声频率、粒径分布以及模型参数结合ECAH[21−22]模型预测理论声衰减谱，同时将其和实测声衰减谱比较，定义误差函数如下：

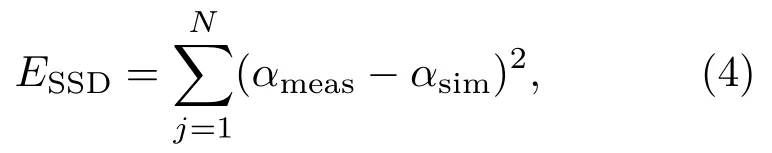
其中，αsim为理论声衰减预测谱，αmeas为实验衰减谱，通过误差函数最小化，即可求解得最优解。

2 改进和声搜索算法

2.1 标准和声搜索算法

和声搜索算法源于对音乐演奏的模拟，设乐器演奏的和声i的状态表示为Xi=(xi1,xi2,···,xiD)，美学评估设为Yi=f(Xi)，即待求目标函数。算法流程如下：

(1)初始化和声记忆库HM：{xi(0)|xLi,j≤xi,j(0)≤xUi,j,i=1,2,···,HMS;j=1,2,···,D}，按照如下方式随机产生：

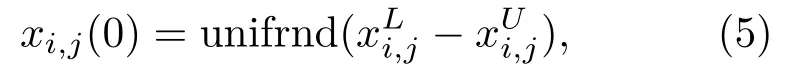
其中，HMS 为记忆库大小，xLi,j和xUi,j分别为xi,j取值的下限和上限，unifrnd为在上下限生成均匀分布的随机数。

(2)基于差分变异创作一个新和声：

其中，HMCR 为和声记忆库取值概率，PAR 为微调概率，bw为微调带宽，r ∈{1,2,···,HMS}。

(3)更新和声记忆库HM：判断新和声目标函数值f(Xnew)是否优于当前和声库中的f(Xworst)，若是，则用新和声代替当前和声库内的最差和声。

(4)是否满足终止条件：若满足停止条件，算法结束；否则重复步骤(2)和步骤(3)，直到满足终止条件。

2.2 拟牛顿法

拟牛顿法是一种较成熟算法，拥有牛顿法收敛速度快的优点，同时用每步梯度信息去近似Hesse 矩阵，减少计算量[23]，基本迭代公式为dk=−Hk∇f(xk)，dk为优化方向，由式(7)BFGS修正公式得Hk：

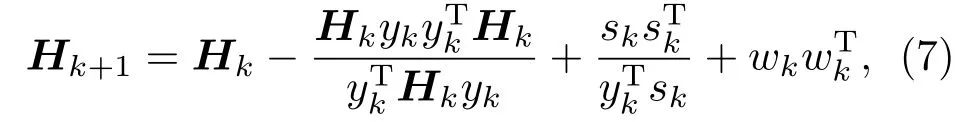
2.3 改进和声搜索算法

作为全局优化算法，和声搜索算法进化到后期，记忆库多样性降低，贪婪选择容易错过一些有潜力的解向量，陷入极小值，致求解精度不高；而拟牛顿BFGS 算法局部开发能力强，搜索结果更依赖于给定初值。由于搜索过程，局部和全局搜索未设也不易设清晰分界线，且前期与后期算法需求不同，为了提高反演准确性，提出将和声搜索算法和拟牛顿BFGS 进行并行计算，HS 全局搜索能力强，将其近似解给BFGS 赋为初值利用其局部搜索能力，提高得到精确解的概率，两者的融合有利于同步提高全局和局部效率。

图1为改进和声算法(Improved harmony search algorithm,IHS)流程，在迭代前期仅使用和声搜索算法，基于差分策略生成新和声全局寻优，待一定迭代次数时，拟牛顿BFGS算法介入，与和声搜索算法并行计算。具体的，将和声搜索算法寻得当前最优解赋给拟牛顿BFGS 作为初值，若BFGS 反演目标函数值小于和声搜索算法所得，则以BFGS 的最优解替代和声搜索种群库里最优解，更新记忆库，直到满足停止条件。

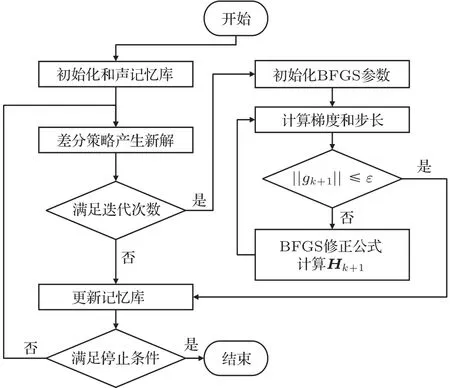
图1 和声搜索算法和BFGS 拟牛顿算法并行计算流程图Fig.1 Harmony search and BFGS quasi-Newton algorithm parallel computing flow chart

3 仿真模拟

3.1 迭代次数

为使IHS 算法搜索解向量过程优化，确定BFGS 介入时迭代次数非常关键。其需满足两个条件：反演的解向量误差小且较为稳定；反演所需时间不能过长。为此，对多个算例进行迭代次数100～900 间的反演，以50 次反演数据均值、方差与反演时长加以比较。表1为R-R 分布(= 20 µm,K= 10)的反演结果，各组特征尺寸均值与设定值偏差为0.05%。

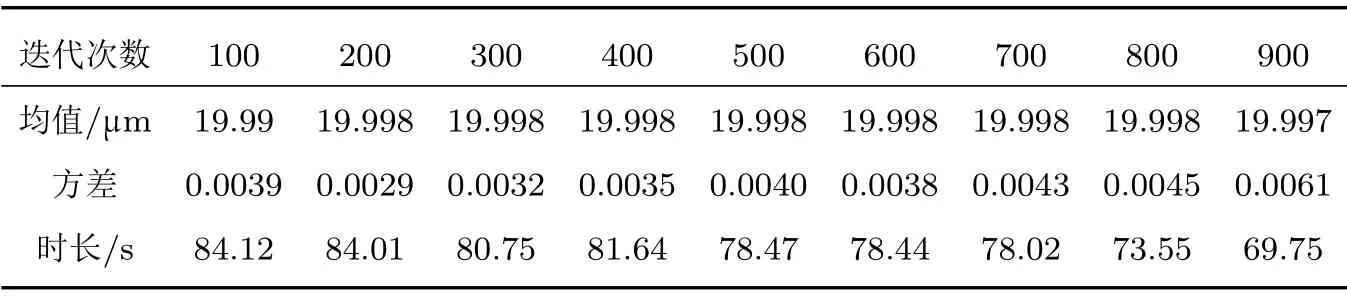
表1 不同迭代次数反演结果Table 1 Inversion results with different iterations

图2给同一R-R分布不同迭代次数的反演结果方差和计算时长，可看出当迭代次数为200 的时候，方差最小，50 次反演结果较为稳定。反演时间随BFGS 介入的迭代次数不同而不同，显然BFGS 在迭代进行到900次时再介入，所需时间最短，但反演结果波动性相较于其他情况更大。介于9 种情况下所需时间相差不大，在一个量级上，迭代次数选择应先满足结果的精确性与稳定性，其次是所需时间，因此可选择迭代次数200次时介入BFGS算法。

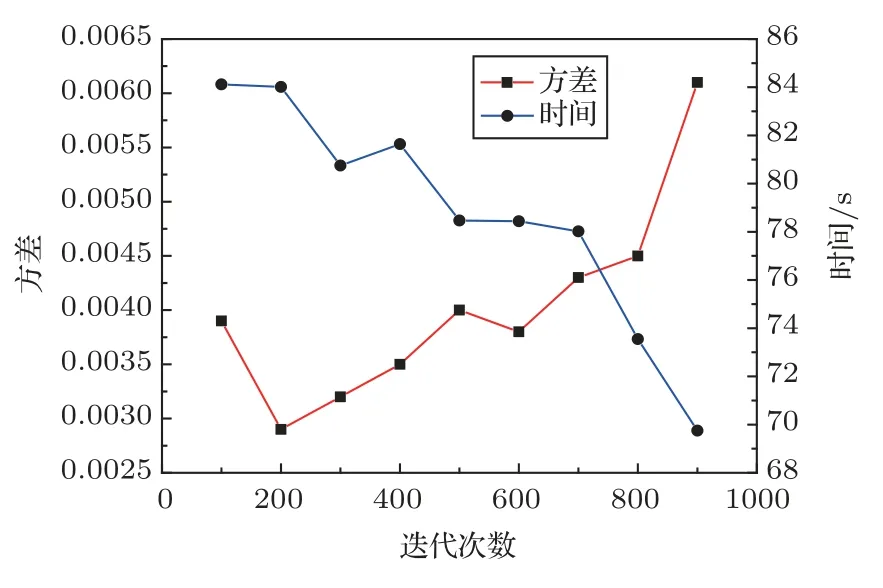
图2 不同迭代次数的方差和时长Fig.2 Variance and computation time required under different iterations

3.2 单峰分布

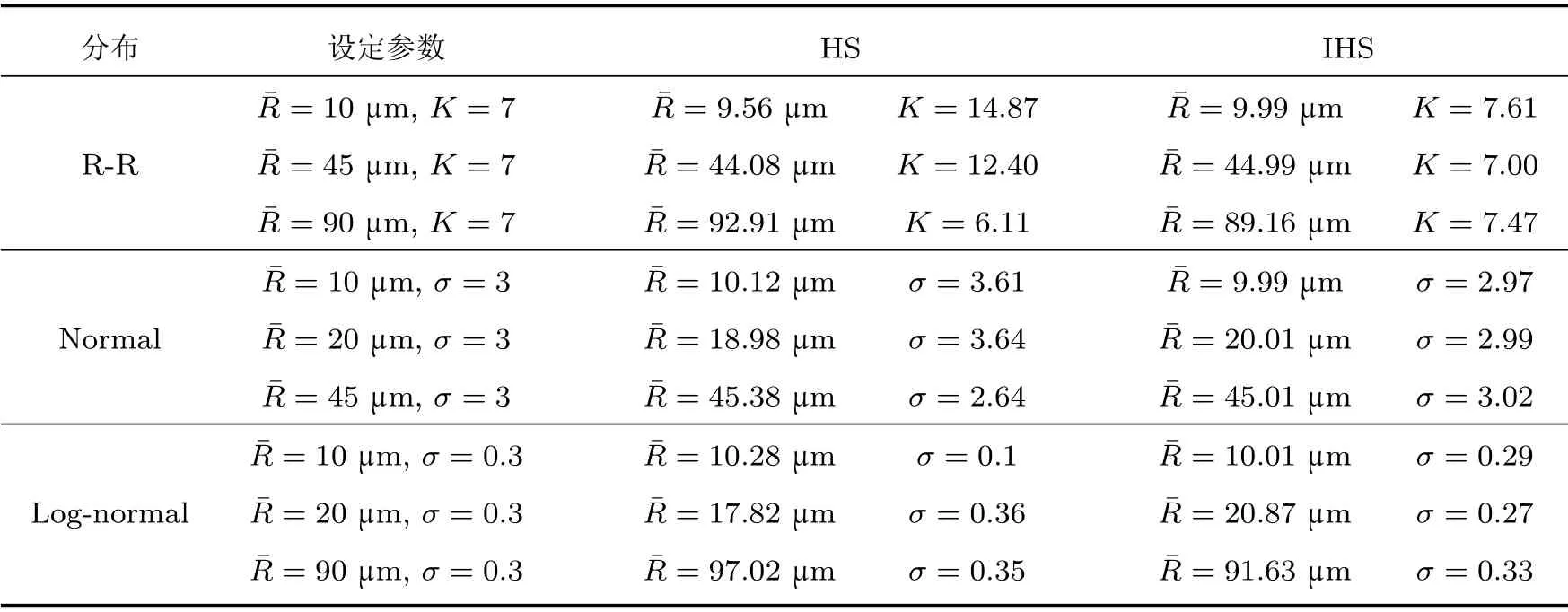
表2 三种分布函数下的单峰参数反演结果Table 2 Inversion results of three kinds of distribution functions by HS and IHS

进一步分析，图3比较了真值σ为3、正态分布不同(10～90 µm)粒径反演，从图3(a)可知，仅粒径= 90 µm 时呈现随机性波动，但最大误差小于5%，其他情况反演结果稳定。对于σ，图3(b)中为70 µm 时，σ值会有少许波动，50次计算中6 次出现大幅度偏差，为90 µm时，增至13次。

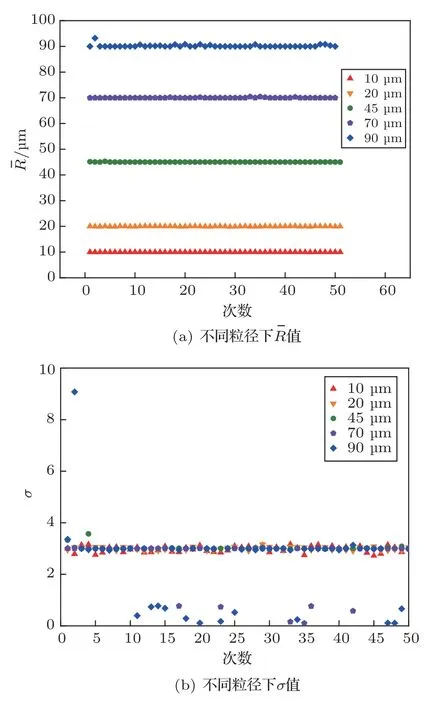
图3 不同粒径下50 次反演变化Fig.3 The change of inversion value of 50 times under different particle size

3.3 双峰分布

反演双峰分布时，需求解参数增至5个(分别用以描述两个分布函数及其配比)。表3数据为双峰R-R 分布反演结果，HS 反演无法取得合理近似值，其求解与真值误差极大，最大误差可至170%。相比之下，IHS 反演峰值位置()与真值偏离较小，最大误差为10%，分布参数K值亦有较明显偏差。

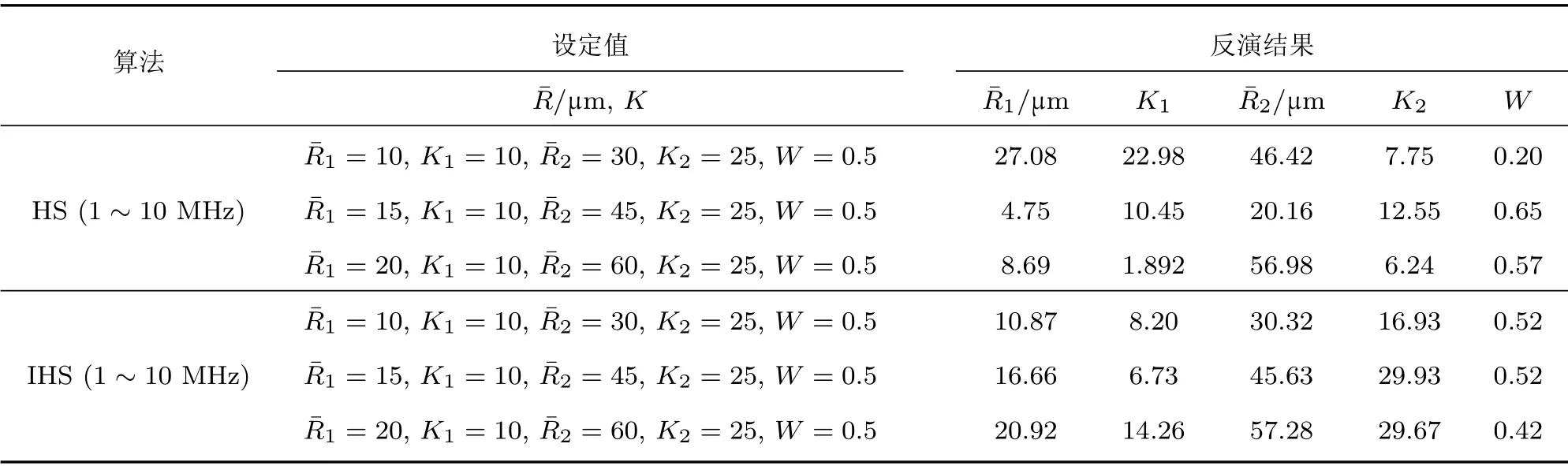
表3 R-R 分布函数下的5 个参数反演值Table 3 Inversion results of R-R distribution functions by HS and IHS

3.4 抗噪性分析

由于实验超声谱测量中往往会引入误差(如实验噪声或信号谱分析误差)，为模拟真实环境中随机噪声或其他干扰，考核算法实用性，在计算衰减谱时人为加入了1%～5%的随机误差。

按照表4设定参数，将50 次分析结果和初始设定进行对比，结果如图4所示。当设定R-R 分布= 70 µm、K= 10，在1%、3%随机噪声下反演值为69.83 µm 和69.77 µm，在95%置信水平下的置信区间分别为(69.825～69.838 µm)和(69.765～69.777 µm)，可见反演结果基本稳定在噪声水平内，没有放大。当随机噪声继续增至5%，寻得平均值为69.36 µm，误差从0.2%增大到0.9%，粒径参数保持稳定。对于分布参数K，随机信号1%、3%时误差为2.15%、15.7%，随机信号5% 时，误差可增至19.66%，可见对R-R 分布而言，分布参数的反演难度更大。

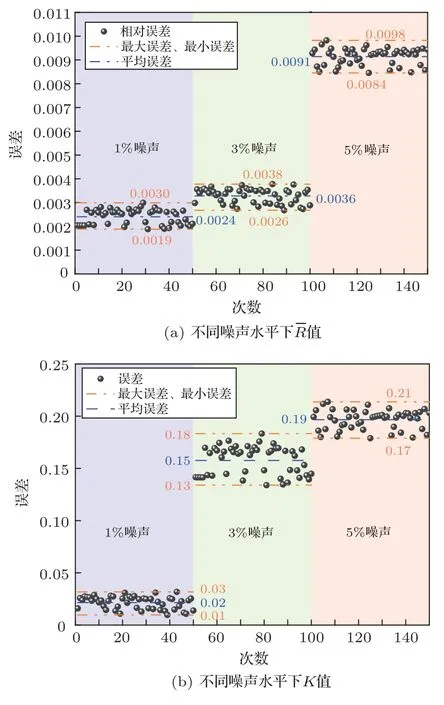
图4 不同噪声水平下50 次反演变化Fig.4 The change of inverse value of 50 times under different SNR

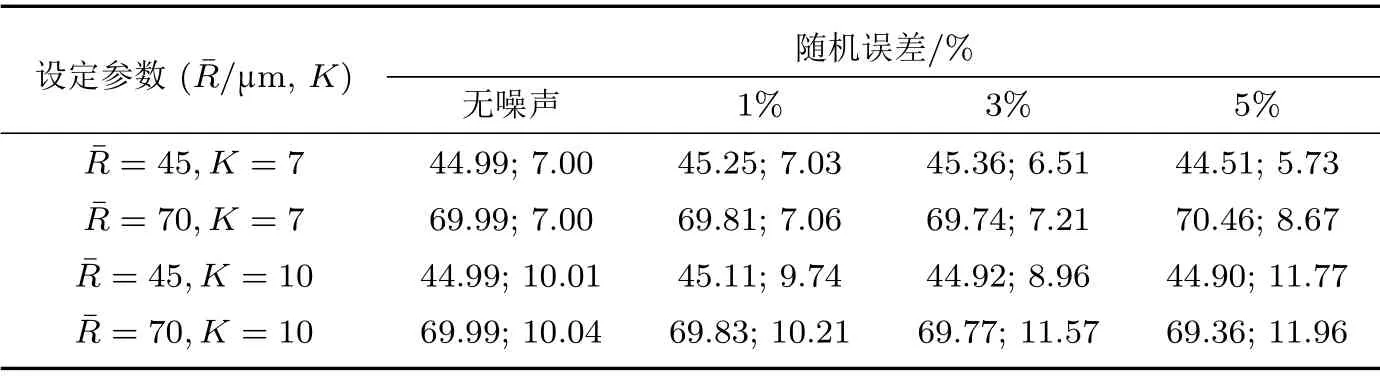
表4 加入不同随机噪声IHS 反演结果Table 4 Inversion results of IHS with different random noise

由于理论上超声有效带宽越宽，所能获得颗粒信息越充分，更利于提高反演精度。因此，针对同样算例，仍在上述3 种噪声情况下将频谱范围拓宽50%(1～15 MHz)加以分析。反演结果的误差减小为0.11%、0.28%、0.36%；分布宽度K误差为则依次2.1%、4.49%，7.36%。可见增加频谱范围，反演误差变小，提升了抗噪性。同时在噪声情况下，进行了迭代次数为100～900的9 种BFGS算法介入情况反演分析，仍是迭代次数为200时，反演结果方差最小，最为稳定。考虑到实验室条件下超声谱的测量噪声水平可控制在1%～2%，结果表明IHS 对颗粒系的反演是有效的。

4 实测颗粒反演计算

4.1 实验原理和装置

图5为测量超声反演信号的装置简图，测量区为6.5 mm。为避免温度波动影响， 实验中将样品池置于循环低温恒温水槽内，温度设定为(20±0.5)◦C。使用了两块等厚度的有机玻璃缓冲块，安装发射/接收信号超声探头(Olympus V310、中心频率为5 MHz)，在激励源(汕头超声，型号CTS-8077PR)作用下自发自收模式工作。双通道数据采集卡(NI PCI-5133，100 MS/s)分别采集样品池内介质为空气或被测样品时的缓冲块-样品界面反射信号A1g、A1s，以及样品池内介质分别为水或被测样品时的样品-缓冲块界面反射信号A2w、A2s，衰减系数表达式为

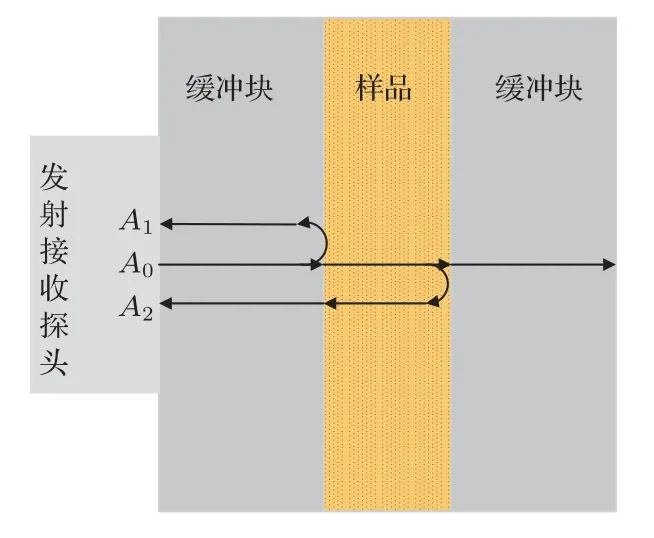
图5 超声测量原理示意图Fig.5 Schematic diagram of ultrasonic measurement principle

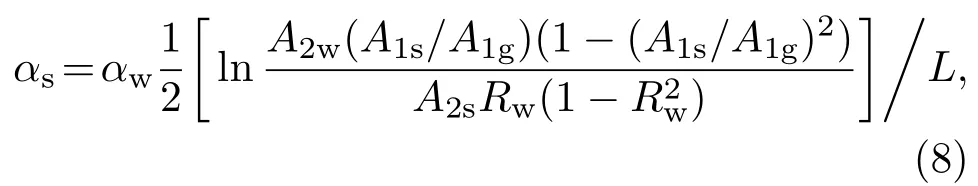
其中，αw是水的衰减系数，Rw是缓冲块与水之间反射系数，L为样品池厚度。

4.2 样品反演计算

实验样品为两种不同粒径的硅-水悬浊液，颗粒密度为2.34 g/cm3，体积浓度均为10%，图6为测得的实验超声衰减谱。图7是分别用HS、IHS 法对衰减谱的反演结果，均较好地区分出两种颗粒。对于标称尺寸为(10±0.6)µm、(20±1.2)µm 硅颗粒由IHS 反演得体积中位径(Dv50)分别为10.61 µm和21.64 µm，反演结果与标称值误差分别为6.0%和8.2%，HS 算法反演结果则较明显偏离真值。相同样品的显微镜图像分析Dv50分别为10.41 µm 和19.54 µm(欧美克公司PIP8.1 图像分析仪，重复性误差<3%)。超声测量误差略大于图像分析，除反演误差外，还可能与硅颗粒的非球形度、超声谱测量误差有关。

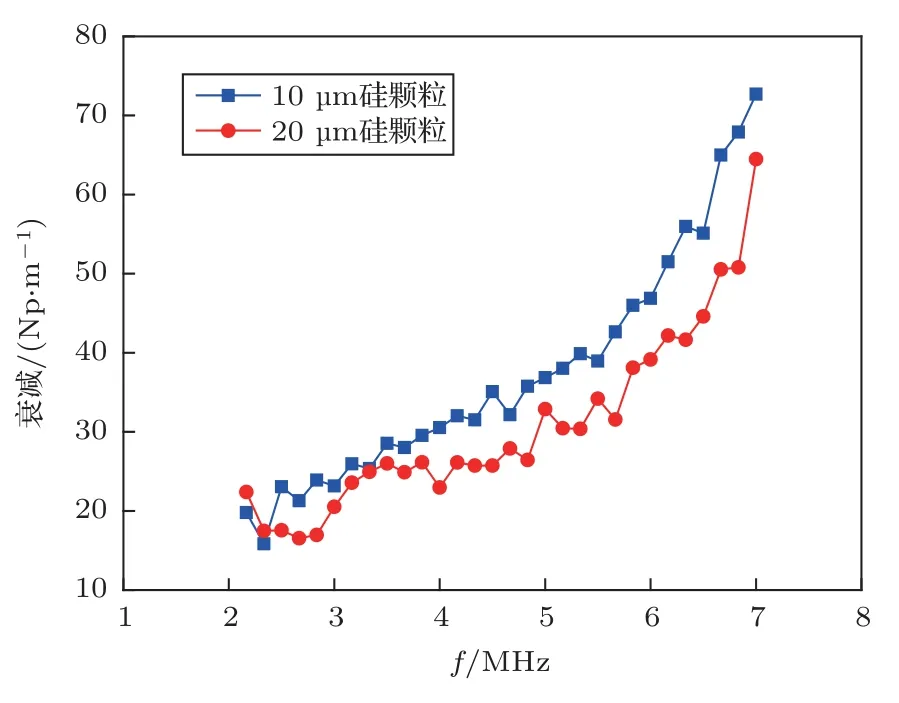
图6 样品实验衰减谱Fig.6 Ultrasonic attenuation spectra of silicon particles

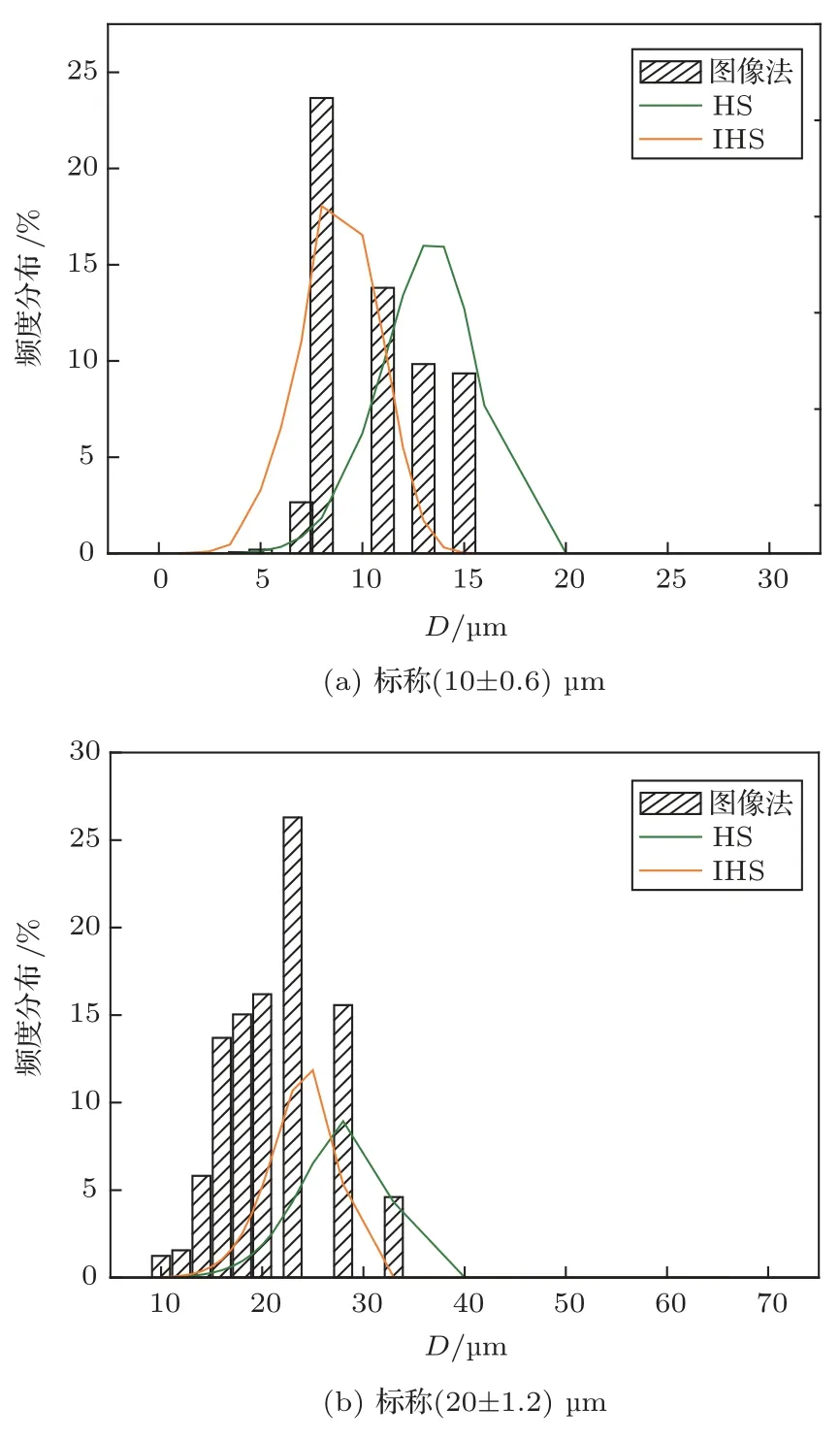
图7 两种方法结果对比Fig.7 Comparison of the results by Image analysis and Ultrasonic spectrum

5 结论

本文主要对和声搜索算法在超声衰减谱法颗粒粒径测量的反演问题进行了研究和讨论，得到了以下结论：

IHS迭代次数为200次时，BFGS开始介入的改进算法试反演优化结果精确度和稳定性最好，但反演所需时间较长；通过多次模拟，IHS 算法反演结果误差均小于10%，优于HS 算法(极端误差可达170%)，其反演精度还可结合更宽频带的谱得以提高；通过实验及与图像法对比进一步验证表明IHS具有较强的实际应用性。本文工作表明IHS 算法相较于HS 算法在反演准确性和抗噪性方面均得到了明显改善，在超声衰减谱法粒径表征具有较好的实际应用价值。