考虑空间变异性的地基极限承载能力上限有限元分析

王曙光，夏鹏，董潇阳，赵志刚

(1.贵州省交通规划勘察设计研究院股份有限公司，贵州 贵阳 550081;2.武汉综合交通研究院有限公司;3.中南大学 土木工程学院；4.中铁七局集团有限公司)

1 引言

岩土体为天然材料，不同于钢筋、混凝土等人工材料，由于现实条件下岩土体受到地质、气候等自然因素以及人为因素的影响，土体的强度参数在空间中呈现出明显的非均质性，这种性质也被称作土体参数固有的变异性。为了描述土体参数的变异性，常通过构建随机变量模型来表征土体参数的不确定性。然而土体参数在经过漫长的沉积作用和后沉积作用后，其参数在空间中呈现变异性的同时又表征出一定的相关性，因此采用随机变量模型已无法客观和真实地表征实际土体参数在空间中的分布特征。相较于随机变量模型，采用通过引入随机场理论而构建的随机场模型来表征土体参数的空间变异性则更加合理。自随机场理论诞生以来，国内外众多学者将其应用于岩土工程领域，对岩土工程参数的变化规律进行定量分析，截至目前，已取得了较多的研究成果。在岩土工程分析过程中考虑岩土体参数随空间的变化特性来更为真实地模拟土体参数的实际情况已经成为一种趋势。而如何更为精确地求解出地基的极限承载能力，已成为岩土工程领域中的一个研究热点。近年来，越来越多的学者将随机场理论与求解地基极限承载能力的过程相结合，Sung Eun Cho et al.采用随机场理论考虑土体参数的空间变异性及参数间的互相关性对条形基础的极限承载力的影响；Griffiths,D V et al将随机场理论与非线性有限元算法相结合，对考虑剪切强度参数空间变异性的刚性条形基础的承载力进行概率分析；Yongxin Wu et al.将不排水抗剪强度参数建立为非平稳随机场，考虑参数变异性对条形基础地基承载力的影响。对于地基极限承载能力的分析和计算，当前最为常用的分析方法和研究理论主要划分为以下几种：极限平衡法、滑移线场法和极限分析方法。极限分析上限法作为一种新型的岩土工程研究手段，已得到了广泛应用。杨峰等构造出网格状的刚性滑体破坏模式以此处理均质地基，以极限分析上限法作为理论基础并巧妙地利用非线性优化程序进行求解；赵炼恒等将极限分析理论应用于地基承载力，进行了诸多探索，得到了良好的研究成果。

随着计算机技术、设备、算法的不断进步和优化迭代，数值分析方法取得了极为迅速的发展，其中以极限分析和有限单元法相结合的极限分析有限元法表现出了较强的优势，当前越来越多的学者采用极限分析法和有限单元法相结合的研究方法对岩土工程领域内所面临的诸多复杂的理论方法和技术难题进行探索。Sloanet al.、Hjiaj et al.在极限分析有限元法方面做了大量的探索工作，取得了开创性的研究成果。OptumG2是由澳大利亚和欧洲的教授和工程师联合开发的一款极限分析有限元软件，因其操作界面简单、收敛性强的特点被广泛应用于各类岩土工程实践中，在分析复杂地质条件、复杂支挡结构的破坏模式分析、地基承载力分析、可靠度分析等方面具有独特的优势。

基于以上考虑，该文引入随机场理论，考虑地基土体参数的空间变异性，对地基极限承载能力进行上限有限元分析。利用OptumG2软件考虑两种不同的参数变化模式，将土体参数随空间的变化情况分为两种模式分别进行建模分析：① 假定处于基础下方土体的黏聚力随着深度的递增而线性增大，将黏聚力随深度的变化情况分为3种变化梯度，对计算结果进行对比分析，研究地基承载力随黏聚力分布形式的变化规律；② 同时考虑黏聚力在水平和竖直方向上的变异性，假定处于基础下方地基土体黏聚力的分布服从高斯随机场，研究土体的黏聚力均值、变异系数、水平相关距离和竖直相关距离等参数的变化对地基极限承载能力的作用效应。

2 考虑空间变异性的地基模型构建

2.1 模型构建

将基础定义为刚性材料，基础尺寸设置为宽度B=2 m、高度H=0.5 m，在基础左右两侧施加法向约束；地基土体尺寸设置为宽度30 m、高度10 m，在地基左右两侧和底部边界施加标准边界约束。地基破坏模型见图1。

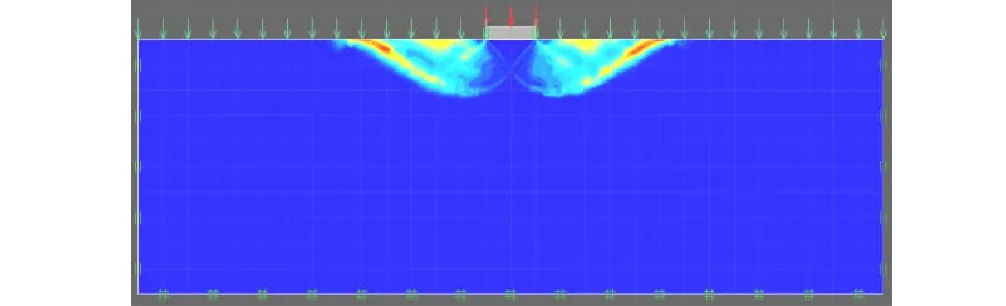
图1 地基破坏模型

2.2 有限元模型

考虑两种参数分布形式分别进行建模讨论：

(1)黏聚力值随深度的递增而线性增加

黏聚力随深度变化如图2所示。基础下方土体服从M-C破坏准则，取基础下方土体黏聚力均值为30 kPa，黏聚力随深度增大取不同的梯度，分别以1、2、3 kPa/m的梯度增大。

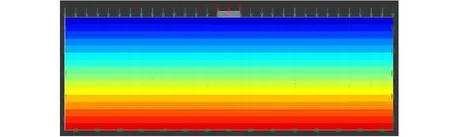
图2 土体的黏聚力值随深度变化

(2)黏聚力按平稳随机场分布

地基模型如图3所示。平稳随机场指的是参数的均值和标准差与点在空间内所处的绝对位置无关，而仅与两点间的相对位置有关。该文假定参数随机场遵循平稳性假设，且土体黏聚力服从高斯分布，研究黏聚力的均值Uc、变异系数a、水平相关距离CLx和竖直相关距离CLy对地基极限承载能力的作用效应。

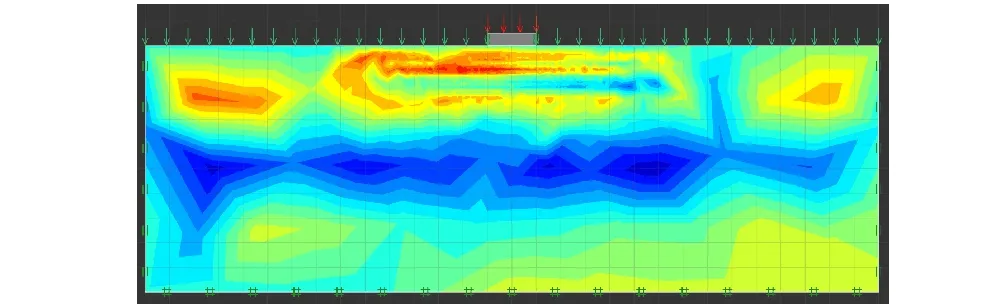
图3 土体黏聚力值按随机场分布

3 地基极限承载能力上限有限元分析

3.1 黏聚力随深度线性增大时地基极限承载力的计算与分析

首先对黏聚力值随深度呈线性增加的情况进行分析，黏聚力分别以1、2、3 kPa/m的梯度增大时，研究内摩擦角φ、黏聚力均值Uc、外加载荷q和土体重度γ对地基极限承载能力的作用效应，并将计算结果与均质地基情况进行对比。参数取值见表1。

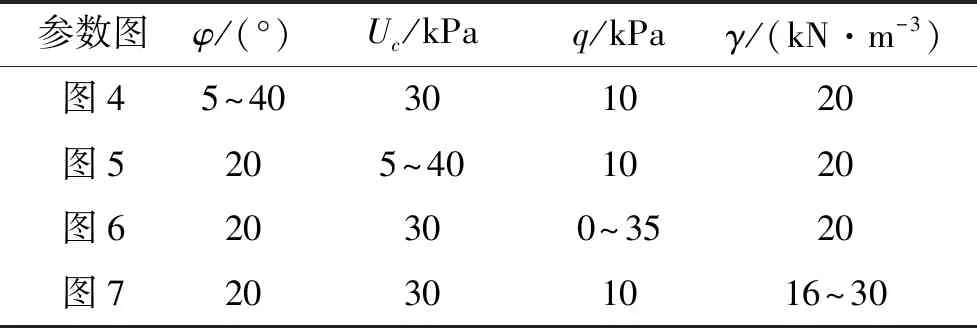
表1 参数取值

(1)φ对地基极限承载力的作用效应(图4)

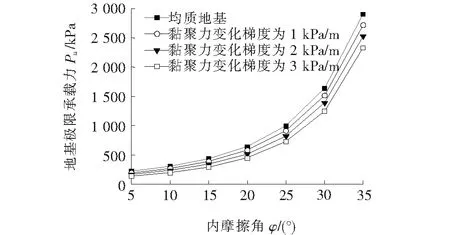
图4 极限承载力随φ的变化曲线

由图4可知：在线性M-C条件下，对比各变化梯度下计算出的相应地基极限承载能力的计算结果，从大到小依次是均质地基数值模拟、黏聚力为梯度1 kPa/m数值模拟、梯度2 kPa/m数值模拟、梯度3 kPa/m数值模拟。可以得到如下结论：随着φ的增大，不同变化梯度下计算得到相应的极限承载能力均不断增大；而且φ越大，在不同变化梯度下计算得到的相应的极限承载能力的差值也会越大；并且当土体的黏聚力值随深度变化的梯度变大时，计算得到的相应的极限承载能力值会减小。

(2)Uc对地基极限承载能力的作用效应(图5)

由图5可知：在线性M-C准则条件下，对比以上地基极限承载能力计算结果，从大到小依次是均质地基数值模拟、黏聚力为梯度1 kPa/m数值模拟、梯度2 kPa/m数值模拟、梯度3 kPa/m数值模拟；随着Uc的不断递增，不同变化梯度下计算得到的相应的极限承载能力值均不断增大；并且土体的黏聚力随深度的变化梯度越大，计算得到的相应的极限承载能力值越小。

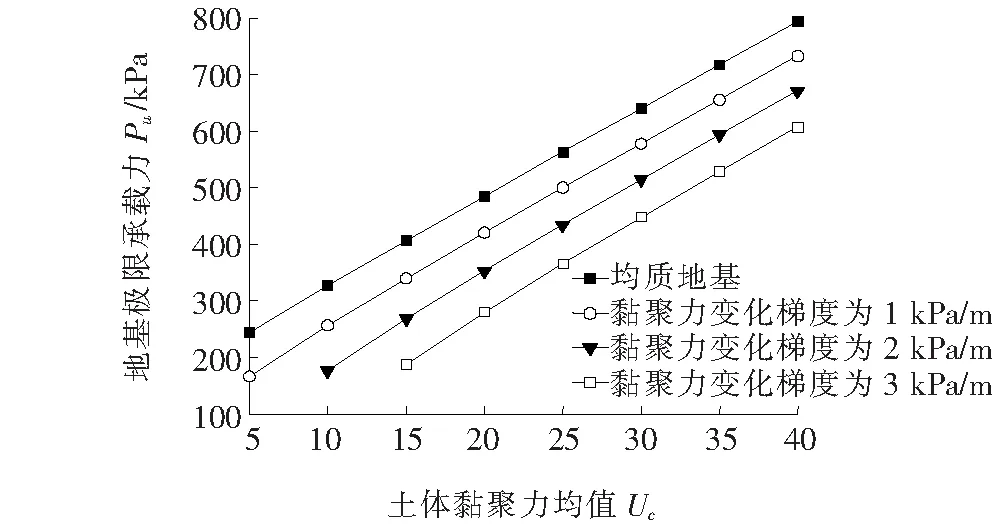
图5 Uc对极限承载能力的作用效应曲线

(3)外加载荷q对极限承载能力的作用效应(图6)

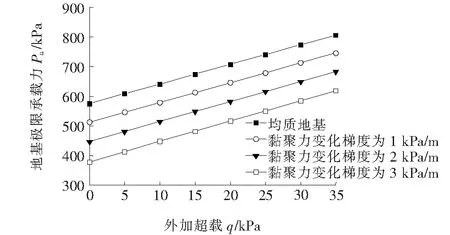
图6 外加载荷q对极限承载能力作用效应曲线

由图6可知：在线性M-C条件下，对比以上地基极限承载能力计算结果，从大到小依次是均质地基数值模拟、黏聚力为梯度1 kPa/m数值模拟、梯度2 kPa/m数值模拟、梯度3 kPa/m数值模拟；随着外加载荷q的增加，不同变化梯度下计算获取的相应的极限承载能力值均不断增大；并且随着土体黏聚力值随深度变化的梯度变得越大，计算得到的极限承载力变得越小。

(4)土体重度γ对地基极限承载能力的作用效应(图7)

由图7可知：在线性M-C条件下，对比以上地基极限承载能力计算结果，从大到小依次是均质地基数值模拟、黏聚力为梯度1 kPa/m数值模拟、梯度2 kPa/m数值模拟、梯度3 kPa/m数值模拟；随着土体重度γ的增大，不同变化梯度下计算得到的相应的极限承载力均不断增大；并且随着土体的黏聚力值随深度变化的梯度变得越大，计算得到的极限承载力变得越小。

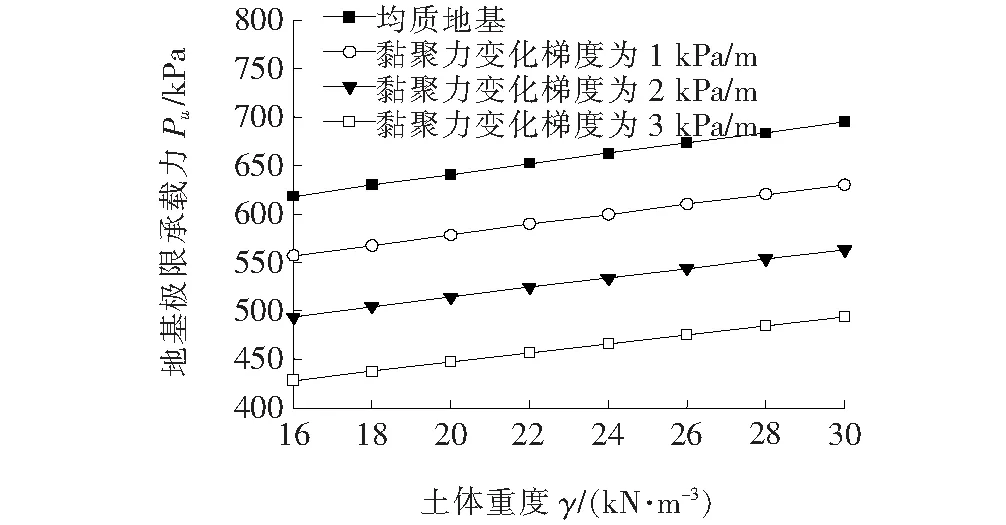
图7 γ对极限承载能力的作用效应曲线

3.2 黏聚力按平稳随机场分布时地基极限承载能力的计算与分析

该节分析当黏聚力参数服从高斯平稳随机场分布时，黏聚力均值Uc、空间变异系数a、水平相关距离CLx、竖直相关距离CLy对极限承载能力的作用效应。使用极限分析有限元软件并采用蒙特卡洛算法来实现参数的随机分布，计算次数为1 000次。模型的几何尺寸为：长30 m，高10 m，基础宽度B=2 m。模型参数取值为：φ=20°，γ=20 kN/m3，q=10 kPa。

(1)Uc对地基极限承载能力的作用效应(表2)

由表2可知：土体黏聚力参数随机场的空间变异系数a=0.2，相应的水平相关距离CLx=40 m，竖直相关距离CLy=1 m时，随黏聚力均值Uc增大，地基极限承载能力计算结果的平均值、最小值和最大值均不断增大。

(2)空间变异系数a的作用效应(表3)

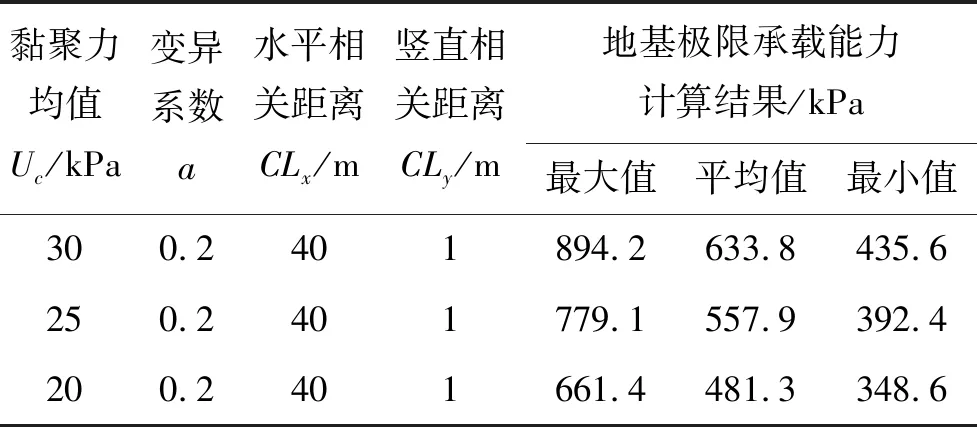
表2 Uc=20～30 kPa时计算结果

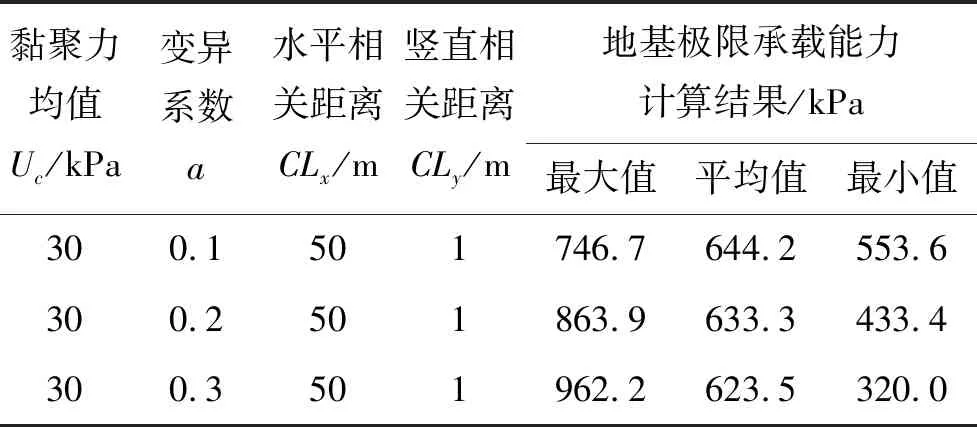
表3 a=0.1～0.3时计算结果

由表3可得：土体黏聚力参数随机场的均值Uc=30 kPa，相应的水平相关距离均为CLx=50 m，竖直相关距离均为CLy=1 m时，随着土体黏聚力对应的空间变异系数a的增大，计算获取的极限承载力的均值和最小值均不断减小，而极限承载力的最大值却不断增大。

(3)水平相关距离CLx的影响分析(表4)

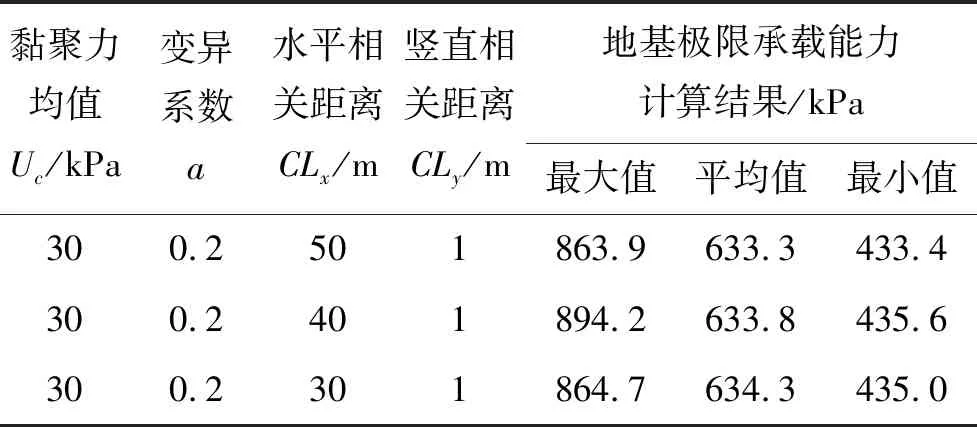
表4 CLx=30～50 m时计算结果

由表4可知：土体黏聚力参数随机场的均值Uc=30 kPa，空间变异系数a=0.2，竖直相关距离CLy=1 m时，随着水平相关距离CLx的增加，极限承载力计算结果的均值有细微的减小，而对其最大值和最小值的影响规律并不显著。

(4)竖直相关距离CLy的影响分析(表5)

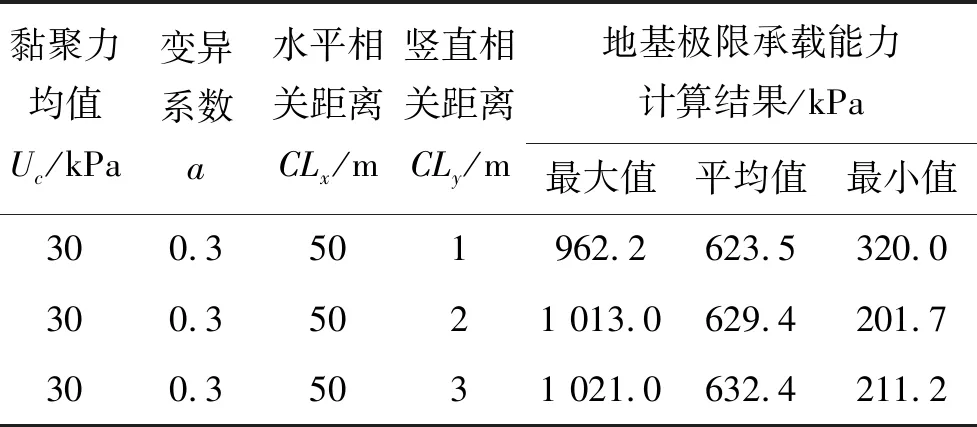
表5 CLy=1～3 m时计算结果

由表5可知：土体黏聚力参数随机场的均值Uc=30 kPa，相应的空间变异系数a=0.3，水平相关距离CLx=50 m时，随着竖直相关距离CLy的增大，地基的极限承载能力计算结果的平均值和最大值逐渐增大，而对最小值的影响规律并不明显。

4 结论

(1)黏聚力均值Uc、内摩擦角φ、外加超载q、土体重度γ，对地基的极限承载能力的作用效应相似，任一参数值增大，均会造成地基极限承载能力增大。

(2)当土体的黏聚力均值相等时，对于黏聚力随深度线性增大的地基，地基的极限承载能力要比均质地基小；土体黏聚力随深度变化的梯度越大，地基的极限承载能力值越小。

(3)黏聚力服从高斯分布时，黏聚力均值Uc越大，相应的地基极限承载能力计算结果的平均值、最小值和最大值均不断增大。

(4)随机场参数会对地基极限承载力产生影响，变异系数a越大，相应的极限承载力的均值和最小值均不断减小，而极限承载力的最大值却不断增大；水平相关距离CLx越大，极限承载力计算结果的均值有细微的减小，而对其最大值和最小值的影响规律并不显著；竖直相关距离CLy越大，地基的极限承载能力计算结果的均值和最大值逐渐增大，而对最小值的影响规律并不明显。