非线性三阶三点边值问题多个正解的存在性
2021-09-22张瑞燕
张 瑞 燕
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
三阶微分方程在数学和物理学领域应用广泛, 如具有常数或变截面的弯曲梁、 电磁波或重力驱动流等. 三阶边值问题是常微分方程中的经典问题, 对三阶边值问题的研究目前已取得很多成果[1-8]. 例如: Guo等[9]考虑三阶三点边值问题

(1)
其中0<η<1, 1<α<1/η.用锥拉伸与压缩不动点定理得到了如下结果:
定理1[9]设f∈C([0,∞),[0,∞)),a∈C([0,1],[0,∞))且在t∈[η/α,η]上不恒为零.若f还满足如下条件之一:
1)f0=0,f∞=∞;
2)f0=∞,f∞=0.
Cabada等[10]用不动点指数定理证明了三阶三点边值问题
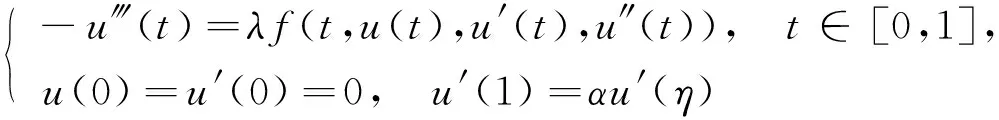
(2)
至少存在一个正解, 其中λ>0为一个参数,f: [0,1]×3→3为L1-Carathéodory函数, 0<η<1, 1<α<1/η为给定的常数.
由于所用工具的局限性, 文献[9]仅在f(u)超线性和次线性增长的情形下讨论了正解的存在性, 未考虑多个正解的情形, 并且文献[9]和文献[10]中, 1<α<1/η, 即α的取值范围依赖于η.对于α>0, 三阶边值问题(2m-1)个正解的存在性研究目前尚未见文献报道.基于此, 本文考虑更一般的非线性三阶三点边值问题

(3)
多个正解的存在性.本文总假设:
(H1)f: [0,1]×[0,∞)→[0,∞)连续;
(H2)ρ>0是一个常数;
(H3) 0<η<1,α>0.
1 预备知识
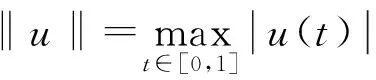
引理1[11]假设X是一个Banach空间,K⊂X是一个锥,T:K→K是一个全连续算子且0 1) ‖Tu‖≤‖u‖, ∀u∈K, ‖u‖=r且‖Tu‖≥‖u‖, ∀u∈K, ‖u‖=R; 2) ‖Tu‖≥‖u‖, ∀u∈K, ‖u‖=r且‖Tu‖≤‖u‖, ∀u∈K, ‖u‖=R. 则算子T有一个不动点u∈K且r<‖u‖ 设φ1(t),φ2(t)分别是问题 和 的唯一解.易得 (4) 且φ1(t)在[0,1]上严格递增,φ2(t)在[0,1]上严格递减. 假设: (H4) 0<αφ1(η)<1. 引理2假设(H2)和(H4)成立,h(t)∈C[0,1], 则边值问题 (5) 存在唯一解v(t), 且 (6) 其中 (7) v(t)=C1(t)φ1(t)+C2(t)φ2(t),t∈[0,1], (8) 则有 (9) 解得 (10) 由式(8)和式(10)得 其中 易得 (11) 下面证明由式(6)定义的函数是式(5)的一个解.由于 因此, 又因为 显然有v(0)=0,v(1)=αv(η).证毕. 令‖v‖=v(t0),t0∈(0,1]. 下面证明 (12) 结论得证. 引理4假设(H2)~(H4)成立, 则对∀δ∈(0,1/2), 存在0<γδ<1, 使得式(5)的解v(t)满足v(t)≥γδ‖v‖,t∈[δ,1]. 证明: 取γδ=min{q(t)|t∈[δ,1-δ]}, 显然结论成立. 引理5[13]假设(H2)~(H4)成立, 且y(t)∈C[0,1], 则问题 (13) 定义集合 显然,K是E上的一个锥.定义算子T:E→E, 引理6假设(H1)~(H4)成立, 则T:K→K是全连续算子. 证明: 下面分两步证明T:K→K是全连续算子. 1) 证明T在K中有定义.显然, 对∀t∈[0,1], 都有Tu(t)≥0, 并且当t∈[δ,1]时, 有 2) 证明T是一个紧算子.由于f(s,u(s))为连续函数, 则对∀s∈[0,1], 存在M>0, 使得|f(s,u(s))|≤M. 先证明Tu(t)在C[0,1]上一致有界.对∀u(t)∈K, 有 所以Tu(t)在C[0,1]上一致有界. 再证明Tu(t)在C[0,1]上等度连续.令t1,t2∈[0,1], 不妨假设t1 定理1令m∈满足rk+1 (i)f(t,u(t))≥Brk,γδrk≤u≤rk,t∈[δ,1],B∈(Λ1,+∞); (ii)f(t,u(t))≤ARk, 0≤u≤Rk,t∈[0,1],A∈(0,Λ2). 令u∈K∩∂Ω2,k, 对∀t∈[0,1], 都有u(t)≤‖u‖=Rk.由条件(ii), 可得 2) 令v∈K∩∂Ω2,k+1(k=1,2,…,m-1), 对∀t∈[0,1], 都有v(t)≤‖v‖=Rk+1.由条件(ii), 可得 综上可知,T共有(2m-1)个不动点. 考虑如下非线性三阶三点边值问题: (14) 其中ρ=1,α=1,η=1/2.不妨取δ=1/4, 经简单计算可得 则 令m∈,α∈,A∈(0,Λ2),B∈(Λ1,+∞), 使得可得rk+1 α-(4k+2)<‖uk‖<α-4k,k=1,2,…,m, α-4(k+1)<‖vk‖<α-(4k+2),k=1,2,…,m-1.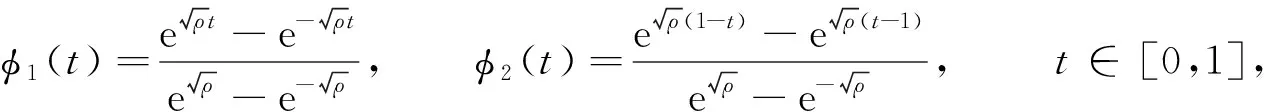


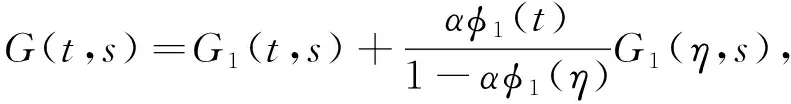





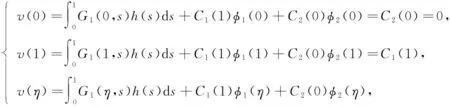
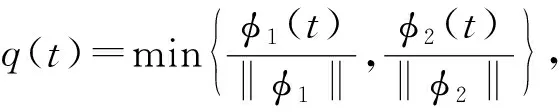

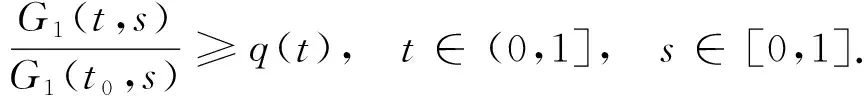

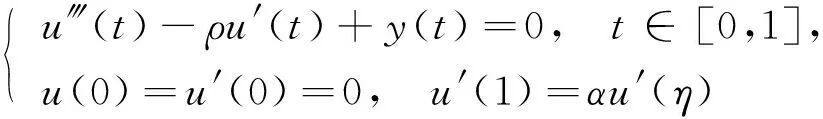


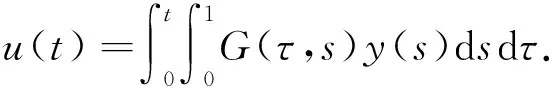
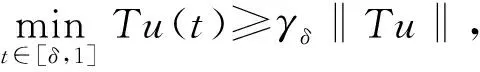
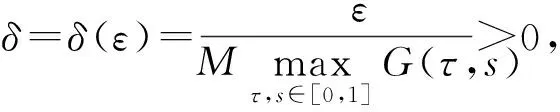
2 主要结果
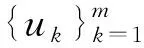


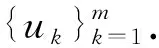

3 应 用


