三角环工业标志符快速高精度定位算法

齐 敏，牛贝乐

（西北工业大学电子信息学院，西安 710129）

引 言

当前电子产品小型化、轻便化、多功能化的发展趋势使电子元器件尺寸越来越小，相应的电子产品中印刷电路板（Printed circuit board，PCB）的集成度也越来越高。表面贴装技术（Surface mount technol⁃ogy，SMT）是一种在PCB 上无需钻孔、直接将表面贴装元器件贴焊到PCB 表面规定位置上的电路装连技术。与传统工艺相比，SMT 技术具有组装密度高、产品体积小重量轻和可靠性高的特点，极为适合当今设备小型化、便携式和高集成度的发展需求，并且易于实现自动化生产，提高生产效率［1］。随着科技的不断发展，代表新一代电子组装技术的表面贴装设备面临着越来越高的技术要求，基于机器视觉的标志符高精度定位技术的优势和重要性愈发凸显。标准工业标志符有圆形和直线型等共10 种，以表面贴装设备流水线上的锡膏印刷机为例，标志符分别印制在PCB 和钢网模板上，通过对标志符几何中心的检测定位，获得PCB 和钢网模板的空间位置信息，用于控制两者的精确对位，从而控制锡膏印刷的精度，因此标志符的定位精度对锡膏印刷的良品率将产生直接影响，是至关重要的指标。目前国产表面贴装设备中的视觉定位软件大多依赖于国外商用软件进行二次开发，主要是美国国家仪器公司开发的NI Vision，采用国外商用软件除了技术上受制以外，也大大增加了设备成本，并且NI Vision 软件仅有圆形标志符的自动定位功能，没有其他标志符的自动检测。目前已有的高精度标志符定位算法主要针对圆形标志符［2⁃3］，面向三角形、矩形等直线型标志符的研究很少。本文根据实际应用需求，研究三角环标志符的高精度检测定位算法，为具有完全自主知识产权的中高端表面贴装设备的国产化替代产品提供底层技术支撑。一般工业标志符的外接矩形边长为1~3 mm，图1 为工业相机拍摄的三角环标志符的放大图像。

图1 工业相机拍摄的三角环标志符放大图像Fig.1 Enlarged images of triangle ring mark tak⁃en by industrial camera

常见的中心定位方法有重心法［4］、模板匹配算法［5］和基于边缘检测的算法［6⁃8］等。重心法对检测形状进行图像分割后求取其重心，虽然检测速度快，但对图像质量要求高，但精度不高。模板匹配算法根据滑动窗口内的像素灰度特征或检测对象的形状特征，检测图像中与已知模板匹配度最高的区域，但是依据像素灰度的方法存在旋转缩放时检测速度慢、精度低和鲁棒性差的问题；依据形状特征的方法在图像较为复杂、干扰较多时检测效果不佳。基于边检测的算法包含霍夫变换方法［7］和直线拟合方法［8］应用于三角环的检测定位时效果相对较好，但仍有以下问题：霍夫变换方法鲁棒性好，但存在计算量大、检测速度慢等缺点；直线拟合方法精度高，但当三角环的顶点由锐角退化成圆弧状的拐角时，会对三角环标志符直线边的拟合精度造成直接影响。

为了解决上述问题，本文提出一种面向三角环标志符的精度高、鲁棒性好的中心定位算法，该算法基于凸包分割技术［4，9⁃11］，获取用于拟合三角环轮廓的高精度数据集，再结合直线拟合［5，12⁃13］本身的高精度特性，实现三角环标志符几何中心的快速准确定位。本文提出的算法适用于一般质量的图像，对图像质量无特殊要求。

1 定位算法流程

本文研究的三角环工业标志符高精度定位算法基于凸包分割技术，算法流程为：对三角环标志符图像进行二值化处理后，获取其内环和外环的初始轮廓点集；对外环轮廓进行处理，研究凸包和凸点的几何特征用于轮廓分割，生成外环的轮廓段集合；对轮廓段集合中的所有轮廓段分别进行直线拟合，并利用其斜率特征进行聚类，得到外环三条边各自的有效点集；构建偏离值直方图，设定合理阈值，进一步剔除有效点集中引起细微凹凸和毛刺的干扰像素点，获取用于拟合的原型边点集；基于最小距离直线拟合，高精度重构三角环外环直线边，求得外环的精确几何中心。类似地，获得内环的精确几何中心，进而通过数学平均求得三角环标志符的精确几何中心坐标，实现高精度定位。算法流程如图2所示。

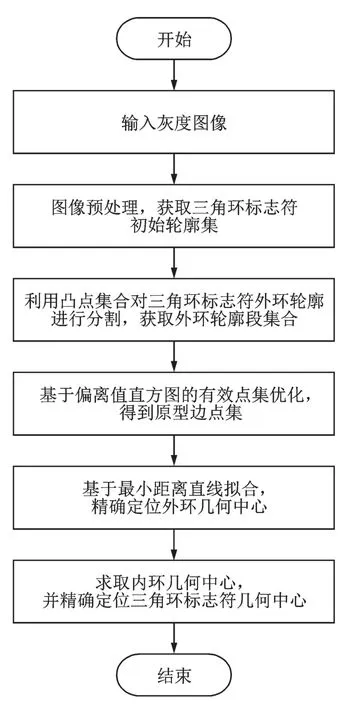
图2 三角环标志符定位算法流程图Fig.2 Flowchart of triangle ring mark positioning algorithm

2 定位算法

2.1 三角环标志符初始轮廓集获取

在工业现场环境中，由于受光照、曝光等因素的影响，所获标志符图像不可避免含有噪声，首先进行去噪处理［14］。然后采用OTSU 算法进行二值化阈值计算［15］，该算法是一种全局化的动态二值化方法，其基本思想是设定一个阈值将灰度图像根据灰度的大小分成前景和背景两个部分，当这两个类的类内方差最小和类间方差最大时，得到的阈值为最优的二值化阈值［16］。据此原理得到二值图像Ib=f（x，y），其中1 为背景像素，0 为标志符图像。采用Canny 算子进行边缘提取［17］，获取三角环标志符的初始轮廓集T为

式中：k=1 表示三角环标志符的外轮廓；k=2 表示三角环标志符的内轮廓。

2.2 基于凸包分割的外环轮廓段集合获取

在对获取的图像进行预处理后，三角环标志符的内、外轮廓均为像素构成的点集。对于二维平面上的点集，包含某个点集所有点的最小凸多边形称为凸包，凸包上的所有顶点称为凸点。如图3 所示，对于五角星区域的点集G，五边形V1V2V3V4V5为点集G的凸包，5 个顶点V1、V2、V3、V4和V5为凸点，本文利用凸包和凸点的性质［18］研究三角环标志符的轮廓分割方法。首先提取三角环标志符外环轮廓的凸点集合，利用凸点集合对外环轮廓进行分割，获得外环轮廓的轮廓段集合。

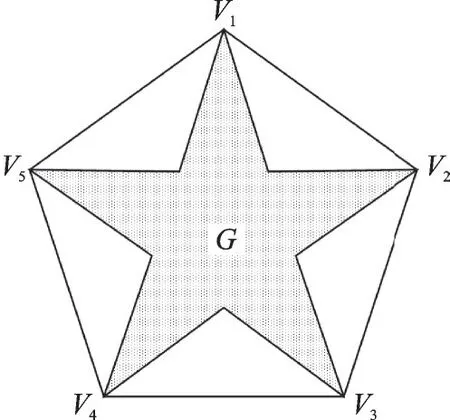
图3 凸包及凸点示意图Fig.3 Schematic diagram of convex hull and convex points

在放大状态下观察，由于实拍三角环标志符图像中，三角环标志符顶角处的轮廓并非理想的直线夹锐角形状，而是锐角退化为类似于圆弧状的拐角，如图4 所示，此时若将拐角附近的像素点引入三角环直线边的拟合计算中，将影响直线边斜率的拟合精度。考虑到拐角处的凸点较多，且相邻两凸点的距离较小，利用凸点进行分割，外环轮廓将被分割为长短不一的轮廓段，拐角附近的轮廓段短小。筛除长度较小的轮廓段即可消除圆弧状拐角对拟合三角环直线边的影响，极大提高算法的精度。

图4 三角环标志符的弧状顶角Fig.4 Arc corners of triangle ring mark

首先寻找外环轮廓的所有凸点：在外环轮廓上的所有点中寻找坐标x，y最小的点C0（x0，y0），其余点记为Pi（xi，yi），i为［1，Q-1］区间的整数，Q为外环轮廓上点的总数量。计算Pi与C0点的连线与x轴之间的幅角α为

依照幅角α从小到大的顺序对各个点进行排序，当α相同时，距离点C0更近点优先排序，即为P1，P2，P3，…，PQ-1。

将点C0和P1放入外环轮廓凸点集合C中，设len为集合C中点的数目，从 点P2（x2，y2）开始遍历，记遍历点为Pi(xi，yi)，若Pi与Clen(xlen，ylen)、Clen-1(xlen-1，ylen-1)满足

则确定将点Pi放入凸点集合C中，len值加1；否则将Clen(xlen，ylen) 从凸点集合C中移除，len值减1。遍历所有点Pi之后得到外环轮廓凸点集合C为

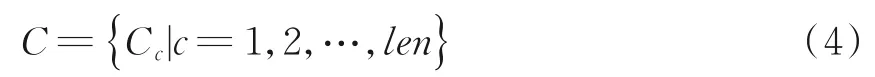
式中：Cc为凸点集合C中的第c个凸点（xc，yc）。此时，可利用凸点分割外环轮廓并筛除长度小的轮廓段。

将凸点集合中的所有凸点及其8 邻域像素置为背景值1，即

式中p，q= -1，0，1。此时外环轮廓被分割为若干轮廓段，计算所有轮廓段的长度，为保证在直线拟合阶段和的有效生成，并减少极端数据对直线拟合效果的影响，筛除长度小于6 个像素点的轮廓段，初步得到用于直线拟合的轮廓段集合D为

式中：Dk为轮廓段集合D中的第k个轮廓段；Qk为轮廓段的个数。

2.3 三角环标志符外环有效点集提取

对集合D中的轮廓段进行基于距离的直线拟合，依据斜率特征，对拟合直线进行聚类，从而实现对应轮廓段的分类，得到三角环标志符外环3 条边的3 个有效点集。

（1）对外环轮廓段集合D 中的所有轮廓段分别进行直线拟合。设集合D 中任一轮廓段的待拟合直线L 的斜截式方程为

则这条轮廓段上的任一点（xi，yi）到直线L的最小距离为

设基于最小距离拟合的目标函数为

分别对F求偏导，令，可解得

记

对式（11）进一步分析，求出参数k为

根据式（10）求出参数b为

将直线的斜截式方程转换成单位化的一般式，可得

由式（12，13）求出参数

因为n-k≥3,故取a∈EXT (u),则存在边取b∈EXT (v),b≠a,则存在边令I=

对轮廓段集合D中的所有轮廓段进行上述相同操作，得到每个轮廓段的拟合直线段。

（2）依照直线斜率特征，利用得到的拟合直线参数，对直线进行聚类。对于集合D中任意两个轮廓段的拟合直线Ls和Lt，若它们的斜率满足式（18），则将它们合并。

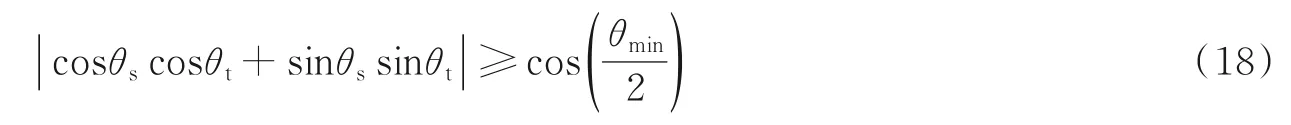
式中：θs和θt分别为拟合直线Ls、Lt与x正半轴的夹角；θmin为两直线最小夹角的阈值，一般设为60°。

（3）对外环轮廓段集合D中的所有轮廓段进行上述合并操作，直至不存在任意两个轮廓段的拟合直线满足式（18），聚类结束。

取外环轮廓段集合D中元素数目最大的3 个轮廓段作为三角环标志符外环3 条边的有效点集，记为S1、S2和S3。

2.4 基于偏离值直方图概念的精确定位

上述得到的有效点集S1、S2和S3去除了外环轮廓中的弧状拐角和凸点等对三角环直线边拟合精度影响大的部分，剩余部分像素点呈良好的直线状分布，但仍带有细微的凹凸和毛刺，如图5 所示。针对这一问题，提出偏离值直方图的概念，进一步对有效点集进行优化，去除其中偏离较大的点，以提高三角环各边直线拟合的精度。

图5 三角环标志符上的凹凸和毛刺Fig.5 Bumps and burrs in triangle ring mark

以S1为例，设其对应边的拟合直线为l1，根据直线方程（14），l1的一般形式为

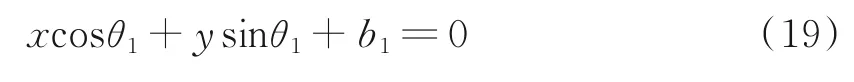
对S1中的任意一点pi(xi，yi)到直线l1的偏离值δi为

计算S1中所有点到直线的偏离值，构成偏离值直方图，使用宽度为h的滑动窗口获取偏离值密度最大区间，得到偏离值阈值（δl，δh）。将S1中所有δi小于δl或大于δh的点从S1中剔除，得到优化后的原型边点集Sa。对于另外2 个有效点集S2和S3进行上述相同操作，获取优化后的原型边点集Sb和Sc。

按照上述拟合方法，利用原型边点集Sa、Sb和Sc对三角环外环3 条边分别进行最小距离直线拟合，高精度重构三角环直线边，得到3 条边的拟合直线方程。3 边直线方程两两相交，计算获得标志符3 个拟合顶点的坐标值A（xA，yB）、B（xB，yB）和C（xC，yC），标志符外环的精确几何中心点坐标O1（X1，Y1）为

对三角环标志符的内环进行和外环相同的处理，获得内环的精确几何中心O2（X2，Y2）。由内环和外环的几何中心坐标确定三角环标志符的精确几何中心坐标Oc（Xc，Yc），即

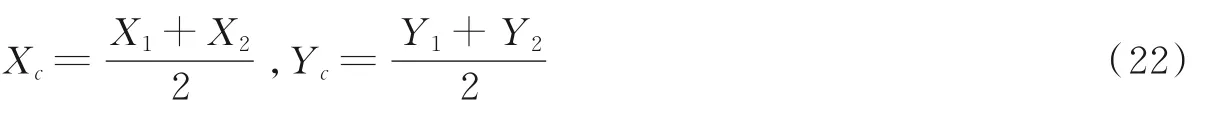
3 实验结果与分析

本文针对印刷电路板和钢网模板上的三角环标志符进行定位实验，设备视觉系统的检测定位误差要求小于10 µm。算法程序运行的操作系统为Windows10 64 位系统，处理器为英特尔Core i7⁃8700K，工作频率为3.70 GHz，内存为16 GB，编程语言是C++，编程软件环境使用的是Microsoft Visual Stu⁃dio 2017，依赖库为图像处理视觉库OpenCV3.4.1。视觉系统采用单色远心镜头工业相机，分辨率为6 µm，相机视觉区域为8.5 mm×5 mm。

3.1 仿真实验

为了验证算法的定位精度，在仿真实验中，模拟实拍图像，制作了由灰色背景、黑色待检测三角环标志符组成的仿真图像，图像为1 280 像素×960 像素大小、8 bit 深度的BMP 格式图像。仿真图像包括不同灰色背景，以及不同位置、大小和旋转角度的待检测三角环标志符，共计30 幅，并分别向其中加入密度为（0，0.02）、（0，0.03）、（0，0.04）的高斯噪声和密度为0.2、0.3、0.4 的椒盐噪声，所有图像构成仿真实验数据集，用于验证算法的正确性、精确性和鲁棒性。图6 为仿真图像示例，其中：图6（a）为一个原始图像；图6（b）的中心位置相对于图6（a）的偏移量为（-96，68），缩放比例为1∶0.64，相对旋转角度-14.2°；图6（c）的中心位置相对偏移量为（82，58），缩放比例为1∶0.58，相对旋转角度为-14.2°；图6（d）的中心位置相对偏移量为（-109，-22），缩放比例为1∶0.58，相对旋转角度为13.0°。位置相对偏移量的单位均为像素。

图6 仿真实验图像示例Fig.6 Images used in simulation experiment

实验中，采用直线拟合法和Hough 变换法对仿真图像进行中心定位，与本算法定位结果进行比较。加入不同密度噪声的仿真图像实验结果如表1 所示，其中定位结果在X、Y方向与标准几何中心的偏差的平均值分别定义为

在X、Y方向的偏差的均方根误差分别定义为

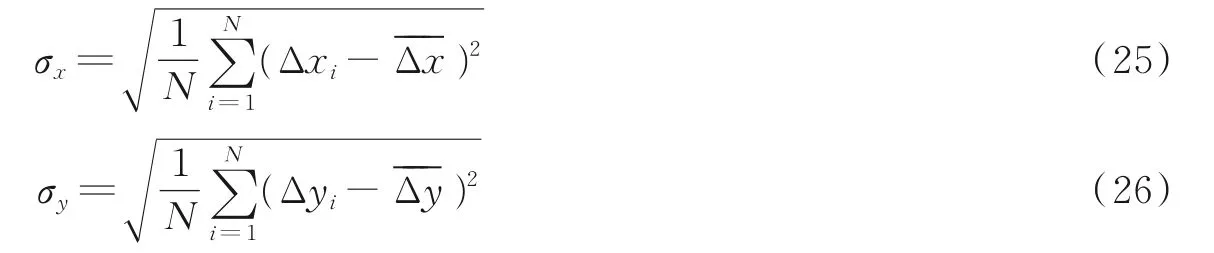
式中：（xi0，yi0）为第i个仿真图像的标准几何中心坐标；（xi，yi）为第i个仿真图像几何中心的定位值；（∆xi，∆yi）为第i个仿真图像的定位偏差；N为仿真图像的个数，此处N=30。

表1 中本文方法中滑动窗口宽度设定为4 像素。实验1 图像的椒盐噪声密度为0.2，高斯噪声密度为0.02；实验2 图像的椒盐噪声密度为0.3，高斯噪声密度为0.03；实验3 图像的椒盐噪声密度为0.4，高斯噪声密度为0.04。由于视觉系统定位误差要求小于10 µm，远心镜头工业相机分辨率为6 µm，而10 µm /6 µm =1.667 像素，因此算法精确度应保证小于1.667 像素。

表1 仿真图像实验结果Table 1 Experimental results of simulation images

从实验结果可以看出，在3 种方法中，直线拟合法的耗时较短，但定位精度差，其原因一方面是由于三角环顶角退化为弧角时使拟合精度变差，另一方面噪声密度的增加使三角环边缘轮廓凹凸情况加重，再次影响了拟合精度。Hough 检测法检测精度较好，面对不同程度的噪声具有一定的鲁棒性，但算法耗时较长，影响设备工作效率，不适合实时检测要求高的应用。在不同噪声情况下，本文三角环定位法耗时短，均可精确地定位到三角环标志符的中心位置。以实验3 为例具体分析，正态分布是一种广泛存在的分布模型，在工程检测中常用3σ 原则进行数据分析。根据3σ 检验原则计算可得，实验3 中直线拟合法的中心定位x坐标偏差范围为（1.603，4.087），y坐标偏差范围为（0.181，0.997），x坐标偏差已无法满足精度要求；Hough 变换法的中心定位x坐标偏差范围为（0.340，1.222），y坐标偏差范围为（0.093，0.171），本文算法的中心定位x坐标偏差范围为（0.118，1.072），y坐标偏差范围为（0.091，0.175），对比Hough 变换法，本文算法的综合检测效果更佳，且平均耗时比Hough 变换法少得多。综上所述，本文算法对三角环标志符的中心定位在精度和速度上的性能最优。

3.2 实测实验

在仿真实验的基础上，本文采用工业场景下的实拍三角环标志符图像进行了实测实验，实验中间过程如图7 所示。其中，图7（a）为实拍三角环标志符图像，图7（b）为经过图像预处理后三角环初始轮廓集，图7（c）为三角环外轮廓的轮廓段集合，图7（d）为三角环外轮廓三条边的有效点集，图7（e）为去除偏移较大点后的3 条边的原型边点集。内轮廓遵循相同的操作，不再列出。图7（f）为对外、内轮廓的3条边进行直线拟合并计算出三角环中心坐标的最终结果。图8 为实际检测的定位结果示例，其中用矩形框标示三角环标志符的位置。

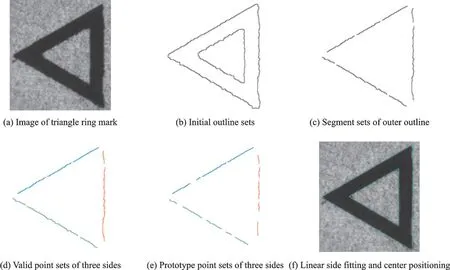
图7 实验环节展示Fig.7 Demonstration of experimental process

图8 实拍图像定位结果Fig.8 Positioning results of images taken by camera

采用3 种算法对图8（a）标志符的中心定位结果如表2 所示。其中x、y方向的标准差分别定义为

式中：M为对一张实拍图像进行定位的次数，此处M=9；（xˉ，yˉ）为实拍图像M次定位数据的算数平均值，即平均中心坐标，（xi，yi）为第i次检测值。从表2 中数据可以看出，直线拟合法的标准差最大，耗时居中；Hough 变换法的标准差居中，耗时长；本文三角环定位算法标准差最小，耗时最短。说明本文算法定位结果的离散度最小，算法的重复性最佳，检测定位性能稳定且耗时少，在高速实时检测要求的基础上，实现了高精度定位。

表2 实拍图像实验结果Table 2 Experimental results of images taken by camera

通过各项实验可以看出，本文算法对三角环标志符实现了快速准确定位，并且对实验图像的质量要求不高，鲁棒性好，能够满足实际工业检测中不同工况下的快速高精度定位。

4 结束语

本文针对表面贴装设备中三角环标志符定位技术不能同时满足精度高、鲁棒性强的问题，提出一种基于凸包分割的定位算法，实现了三角环标志符的高精度快速自动检测定位。该算法将三角环标志符的内环和外环三角形提取出来，分别独立处理，并利用凸包的几何特征将三角环轮廓中的弧状拐角和凸点等剔除掉，避免了圆角效应和位置偏离大的像素点对三角环直线边拟合精度的影响。然后，进一步构建偏离值直方图概念，依此设定合理阈值，剔除细微的凹凸和毛刺，对用于直线边拟合的数据集进行更精细的优化，提高了拟合数据集的质量。在上述基础上，使用最小距离直线拟合算法完成三角环直线边的高精度重构，从而计算出三角环标志符的精确几何中心坐标，实现了三角环标志符的高精度快速定位，能够满足实际应用的需求。