基于标签分布构造的异构数据集年龄估算

王军祥，吴 伶

（1.福建船政交通职业学院信息与智慧交通学院，福州 350007；2.福州大学数学与计算机科学学院，福州 350108）

引 言

基于面部图像的年龄估算旨在找到一种可将面部图像映射到其相应的年龄标签函数。随着诸如安全控制、社交媒体和人机交互等多种实际需求的不断增长，年龄估算越来越受到人们的关注。但由于表情、光照、性别、种族、基因、居住环境与生活方式等许多内在和外在因素的存在，年龄估算问题一直非常具有挑战性。

近年来年龄估算问题研究取得一定的进展，但现有的大多数研究都使用同构数据集年龄估算评估协议，即假定在训练和测试阶段中使用的所有图像都是在相似条件下获得的。但基于同构数据集学习到的模型可能会偏向训练集中图像的特征及分布，从而导致在条件完全不同的情况下年龄估算性能较差。因此在实际的应用中更应该关注异构数据集的年龄估算，即训练集与测试集应具有不同的分布和特征，这样训练后的模型便完全不了解目标数据集的特征，更符合实际场景。

异构数据集评估协议对现有年龄估算方法在实际应用中的效果提出了更高的要求，即要求训练好的模型不仅要在同构数据集下能够准确估算面部图像的年龄，还要在异构数据集下有效地工作。但为了能更好地符合实际场景，并且更好地评估年龄估算方法的泛化性能，本文提出一种异构数据集评估协议。

随着机器学习技术的发展，已有文献提出许多基于深度学习的年龄估算方法。文献［1］提出了一种非线性回归算法，利用分而治之的策略来考虑年龄的位次信息。文献［2］通过训练一系列二元卷积神经网络（Convolutional neural network，CNN）模型获得年龄标签的顺序信息，其中每个二元分类器用来判定输入面部图像的年龄是否超过特定年龄，最终年龄值通过计算CNN 输出的总和而得出。尽管基于回归的方法比较直观，但是性能常常不尽如人意。基于分类的方法［3⁃5］将年龄估算问题建模为一个多类别的分类问题，并将不同的年龄视为独立的类别。在训练阶段，这些方法尝试使用交叉熵（Cross entropy，CE）损失函数来学习判别性特征。文献［6⁃7］对CE 损失函数附加了不同项的正则化，从而惩罚预测年龄与真实年龄之间的差异，其中文献［7］附加了均值方差正则化项，均值正规化惩罚了预测年龄与真实年龄之间的均值差异，而方差正则化项惩罚它们之间的方差差异。文献［8］提出将年龄标签编码为概率分布，以此将年龄标签的局部相关性引入训练过程，这种方法将年龄估计问题建模为分布学习问题。

鉴于损失函数的选择会对域泛化（异构数据集测试）产生巨大影响，本文在分布学习基础上，提出了一种基于分布构造（Distribution construction，DC）的损失函数，以改善在同构和异构数据集场景中模型的泛化能力。在传统的同构数据集评估协议和提出的异构数据集估计协议下，对所提出的损失函数进行实验，在多个数据集下与其他方法进行了比较，结果表明了本文方法的有效性。

1 损失函数对比分析

1.1 问题导入

令{(xn，yn)，n= 1，2，…，N}表示样本容量为N的训练集，其中xn和yn分别代表第n张输入图像及其相应的年龄标签。年龄标签yn是属于年龄标签L={lmin，…，lmax}中的标量值，并且令lmin= 1，lmax=K。年龄估算的目标是学习输入的面部图像xn及其对应的年龄标签yn之间的映射函数。若年龄估算模型使用one⁃hot 编码来表示年龄标签，即标签yn由二进制向量来编码，若面部样本xn属于L中的第k个标签，则，否则。通过此种建模，年龄估算问题就转为了一般的分类问题，其中分类目标是训练CNN 模型以在输入人脸图像xn及其对应的年龄标签sn之间找到映射函数f：xn→sn。然而，年龄估算问题不同于一般的模式识别问题，这是由于相仿年龄的面部通常具有非常相似的图像特征。这种语义相关性会导致视觉标签的歧义性［9］。在one⁃hot年龄标签建模中，通常假定标签是不相关的，而忽略年龄标签的相关性会导致网络训练过程中出现不一致问题［9］。

通过将年龄估算编码为标签分布，文献［8］减轻了训练阶段的年龄标签歧义问题。类似地，本文对于每个输入样本xn也使用标签分布。此时假设qn的每个元素都是在［0，1］范围内的实数，并且约束条件为。根据此定义，年龄标签服从相同的概率分布，此时表示在L中第k个标签的面部样本xn的概率。通过这种类型的建模，年龄估算转化为分布学习问题。此时训练CNN 的目标是通过解决式（1）这样一个最小化问题，求解输入面部图像xn与对应标签分布qn之间的映射函数f：xn→pn，即

式中：L(·)为损失函数；zn=f(xn；Φ) ∈RK表示位于softmax 层之前的CNN 输出；Φ表示CNN 网络的参数。 softmax 函数将向量zn映射为概率分布pn，即范围为［0，1］的实数向量，其总和为1。pn的每个元素（即）表示样本xn属于年龄k的概率，即为。

本文将标签分布定义为高斯分析［10］，即对于每个年龄标签均以yn为中心、以σ为标准差控制年龄分布值的形状（宽度）。对所有年龄段的标签分布，并恒令σ= 2［9］。

此外，不同于大多数年龄估算方法采用的同构数据评价协议，本文提出一种异构数据集评估协议。异构数据集可以看作是域自适应［11］或域泛化［12］。域自适应意味着模型是使用源域中的训练数据而设计的，而工作于与源域完全不同的目标域。一般的机器学习模型便是如此，因为其通常从目标域中获取的有标记数据（即有监督的域自适应）或未标记的数据（即无监督的域自适应）的数量很少。域自适应的方法通常包括将源域中的数据重新映射到目标域，并使用此转换后的源域数据重新设计决策系统。但是在许多场景下，尤其是在年龄估算问题中，采用这种方法是不可行的。例如，假设一个基于域自适应的年龄估算模型正在估算用户上传到其中的测试图像的年龄值，此时若测试图像是从与训练所使用的相同目标域中获得的，则模型将表现良好；然而年龄估算系统要求的是在任何输入图像上都必须表现良好。基于这一重要需求，研究中需要开发一个学习框架，尽管在训练阶段对目标域没有先验知识的了解，但仍然在目标域中表现良好。

与域自适应不同，域泛化指的是预测先前从未了解过的领域中样本的标签，而无需访问目标域。此时便需要在训练过程中获取到任意数量的相关域中的样本，目的是希望所学知识能很好地融合到先前未了解的领域。本文方法基本属于域泛化，差异在于本文方法放宽了在训练阶段必须访问某些相关领域的要求，具体即为本文在一个数据集上训练模型并使用另一个不同的外部环境（例如成像条件等）与内部条件（例如种族等）的数据集进行测试。

1.2 已有损失函数的分析

本文学习算法的主要目标是最大程度地减少预测标签与真实标签分布之间的距离。 现有的CE 和KL（Kullback Leibler）损失函数已被广泛应用于训练使用one⁃hot 编码和标签分布的基于CNN 的年龄估算模型。本节从理论上对这些损失函数进行分析，以说明其在训练基于CNN 的年龄估算模型时的局限性。下文为了简洁起见而省略了索引n。

1.2.1 CE 损失函数

当年龄标签采用one⁃hot 编码时，CE 损失是训练CNN 最常使用的损失函数。该损失假设这些类别是独立的，因此对于年龄估算问题而言，采用CE 损失函数学习到的网络模型会忽略标签相关性。为了缓解此问题，文献［27］将CE 损失函数与均值和方差项结合使用提出CE⁃MV 损失函数，以考虑年龄标签之间的语义相关性，即

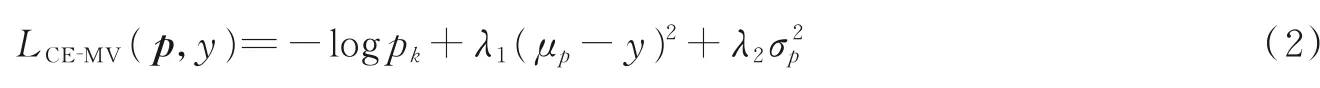
式中：λ1和λ2为正则化参数；μp和σ2p分别为估计分布p的均值和方差。第1 项（交叉熵项）最大化了真实类别的预测概率；第2 项（均值项）惩罚了预测向量p的平均值μp与每个输入样本x的真实年龄标签y之间的差异值；第3 项（方差项）最小化预测向量p的标准差σp。

CE 损失所带来的问题是由于其正规化项而导致的参数训练不稳定，即在训练过程中出现异常值时，正则化项会网络导致较大的误差，从而导致梯度爆炸。

1.2.2 KL 损失函数

当年龄标签被编码为标签分布时，KL 散度是最为常用的训练CNN 的损失函数［8，10］。 KL 损失函数定义为

式中：p和q为预测的标签分布和实际标签分布，该函数的取值范围为[ 0，∞)（若两个分布完全匹配，则LKL(p，q) = 0）且KL 损失函数越低，p与q匹配越好。

KL 损失函数的问题在于它不是对称的，即LKL(p，q) ≠LKL(q，p)。KL 损失函数的这种不对称性会导致：若qk大于pk，则rk=qklog (qk/pk)值为正；反之，若qk小于pk，则会使rk为负，从而导致在整个年龄范围内匹配过程的不均匀性。

KL 损失函数的另一个问题是在反向传播阶段参数的更新规则。KL 损失函数相对于zi的偏导数通过链式法则可以很轻易地得到：∂LKL/∂zi=pi-qi。显然，在使用KL 散度作为损失函数时，模型参数的更新忽略了其他年龄区间值的贡献而只考虑了涉及到的对应年龄标签之间的差值，即pi-qi，这样便会影响到网络收敛后参数的鲁棒性。

与CE 损失函数的改进方案类似，伴有正则化项的KL⁃M 函数为［13］

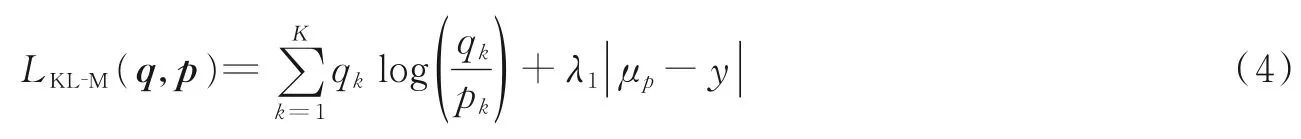
与原始的KL 损失函数相比，KL⁃M 损失函数使用期望回归模块作为正则化项对KL 损失函数的性能进行改善。期望回归模块对估计的年龄分布平均值与真实年龄标签之间的差异进行惩罚。然而，它也具有与CE⁃MV 损失函数相同的问题。

授课结束后，对环境卫生学中的大气部分知识进行测试，试题数量为10道，每道1分，总分为10分。试题内容涉及大气颗粒物、大气污染监测布点、《环境空气质量标准》等。实验班与对照班的试卷相同，比较两班学生对于科研相关知识的掌握情况。

1.2.3 对称损失函数

本节介绍2 个较常使用的对称损失函数，它们解决了之前损失函数的不对称性问题。

（1）f⁃损失函数

令f：R+→R 为凸函数且f(1) = 0，概率分布p与q的f⁃损失函数［14］定义为

当f(x) =-log(x) 时，f⁃损失函数便成为了KL 散度。

由于此损失函数是不对称的，因此在附加对称性后可得到［14］

（2）JS 损失函数

1.3 DC 损失函数

由于使用不同的损失函数会影响参数模型的性能优劣，因此设计一个好的损失函数对基于CNN的年龄估算模型来说相当重要。本文基于分布学习提出DC 损失函数，定义为

式中α为介于0 到1 之间的超参数。当时，DC 损失函数就变为了概率分布p与q之间的f⁃损失函数。当α→0.5 时，提出的DC 损失函数接近文献［16］中的损失函数。

1.3.1 DC 损失函数与用于年龄估算的损失函数的性能比较

对于年龄估算问题，本文提出的DC 损失函数具有以下良好特性：

（1）利用链式法则，提出的损失函数LDC对向量z的每个元素的导数（具体推导过程略）为

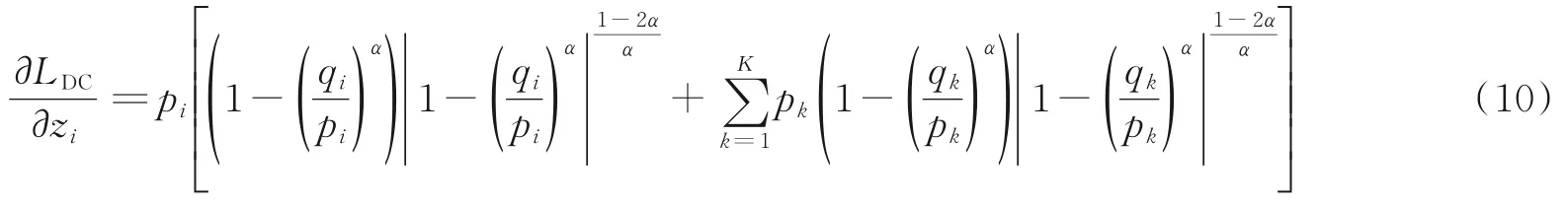
从式（10）可以看出，本文提出的损失函数使得模型参数的更新规则取决于p和q的所有项。 与KL损失函数更新规则仅取决于目标项pi-qi相比，它更加鲁棒。

KL 与DC 损失函数在不同高斯分布下的性能对比如图1 所示，其中图1（a）为2 个原始的高斯分布，图1（b）为KL 损失函数与图1（a）的比率，图1（c）为DC 损失函数与图1（a）的比率。在图1（b）中，两个分布之间的距离在点A和点B处相等，但是在这些点处的r值却不同。因此，当qk大于pk时对总误差的贡献要比qk较小时对总误差的贡献更大。这也意味点A对总误差的贡献要大于点B。因此可以得出结论：在使用KL 损失函数对距离进行最小化后，当qk大于pk时，pk对qk有更好的拟合度；而当qk较小时，则反之。

（2）与现有的损失函数相反，对于［0，1］区间中的任何α值，DC 损失函数都是对称的（图1（c））。由于这种特性，参数的迭代过程将在整个年龄区间范围内均匀执行。

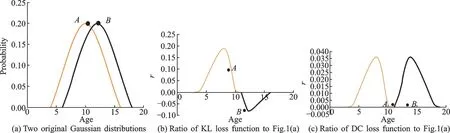
图1 KL 与DC 损失函数在不同高斯分布下的性能对比Fig.1 Performance comparison with KL and DC loss functions under two normal distributions

（3）DC 损失函数解决了稳定性问题，即与CE⁃MV 和KL⁃M 损失函数相比，没有任何正则化项，从而避免了参数波动并有助于网络收敛。（4）与CE⁃MV 和KL⁃M 的关系如下：令α=0.5，此时本文损失函数可重写为

输出为平均值为μp和标准偏差为σp的高斯分布p。此时的C便具有如下闭式表达［17］

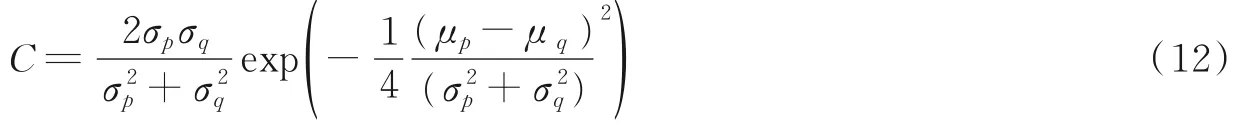
对式（12）取自然对数求相反值后，DC 损失函数的最小值等价于式（13）的最小值。

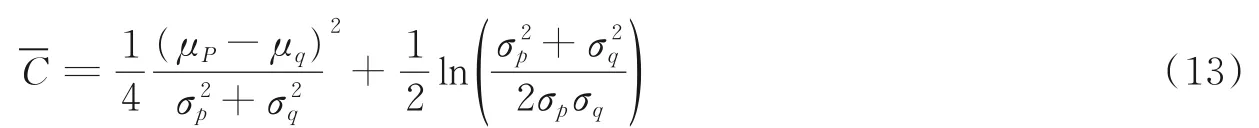
由式（13）可以看出，与CE⁃MV 和KL⁃M 损失函数类似，DC 损失函数隐式地惩罚了年龄估算分布与真实年龄分布之间的差异，并且其年龄估算分布与均值周围。此外，式（13）中的(μp-μ q)2项使用了方差值进行归一化，也减轻了由异常值引起的同样出现于CE⁃MV 和KL⁃M 损失中的不稳定性问题。

1.3.2 DC 损失函数与其他损失函数的性能比较

本节将DC 损失函数与JS 损失函数和χ2⁃统计量进行比较。首先重新构造函数，简单起见下文令α为0.5。通过因式分解和级数展开［18］可以将Lχ2，LJS和LDC与Lf(p，q) =联系起来，其中sk=pk+qk，dk=|pk-qk|。此时每个函数Gf(·) 中的Lχ2，LJS和LDC之间的关系可以推导为

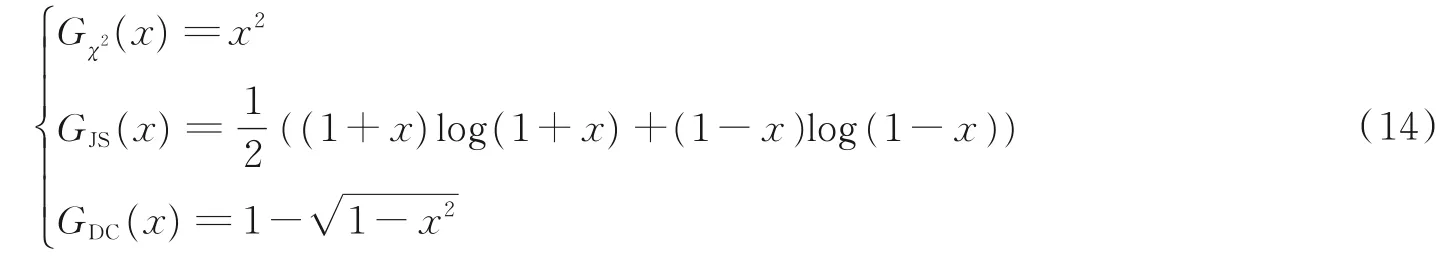
式中：sk∈[0，2]，dk∈[0，1]。

然后分析不同损失函数之间的比率。对于常数sk，比率定义为和，对比曲线如图2 所示。由图2 可见，当误差dk适中时，比率较为平坦；当dk→1 时恰好达到最大比率；而当pk→qk时则达到最小比率。图2 结果为DC 损失函数的相对性质提供了最直观的解释。当误差较大时，DC 损失函数与Gχ2有相似的纠错能力［14］。因此在早期训练阶段，当误差很大时两个函数以相同的方式对误差进行修正。但是，随着训练过程的继续进行和误差越来越小，DC 损失函数将减小误差的影响。当误差接近零时，将不再关注估算分布与实际分布中的对应点，这种属性会减少训练过程对不属于分布点的关注，从而可以稳定训练过程。与GJS的关系同样类似，DC 损失函数总是提供比GJS更强的响应。从图2 可以看出，DC 损失函数在处理不同误差时更具“动态性”［15］。

图2 不同损失函数的比率Fig.2 Ratio of different loss functions

2 实验验证及结果分析

2.1 评价指标

年龄估算的性能主要以2 种度量指标进行评价：平均绝对误差（Mean absolute error，MAE）与累计分数（Cumulative score，CS）。MAE 定义为MAE =，其中lk为测试样本k的实际年龄值，l̂k为估计到的年龄值，N为测试集的样本容量。CS 定义为CS(j)=Ne≤j/N× 100%，其中Ne≤j为测试集中的绝对值误差不低于j的图像总数，本文中的j设置为5。

2.2 数据集

（1）训练集

本文实验选用IMDB⁃WIKI［19］数据集作为训练集。IMDB⁃WIKI 是目前最大的可用于年龄估算的开源数据集，它包含523 051 张图像，且这些图像的年龄标签介于0~100 岁之间。该数据库的图像是直接从网络抓取得到，因此没有经过仔细筛选，所以包含许多不适合年龄估算的图像。虽然文献［5］手动清除了IMDB⁃WIKI 数据库中所有低质量的图像，但是仍然有许多带有错误标签的图像，一定程度上影响了年龄估算的性能。基于文献［5］的结果，本文以一种半监督的方式更加仔细地清理了IMDB⁃WIKI数据库，并删除了所有不合适的图像。首先，本文使用MTCNN 面部检测器［20］检测每个图像中的人脸；然后从数据库中删除了多人图像（因为每个图像只有一个年龄标签）、面部检测器的置信度分数低于检测到的面部阈值（设置为0.9）的图像以及检测到的面部边框尺寸小于一定值（设置为20 像素×20 像素）的图像。 最终，通过人工逐张地检查剩余的图像，并删除所有低质量的图像以及带有错误标签的图像。此外，还从中筛选出了0~100 岁的40 000 张图像，构成IMDB⁃WIKI⁃40k 数据集。相比IMDB⁃WIKI，IMDB⁃WIKI⁃40k 的类不平衡性很好地得到了解决。

（2）测试集

本文实验选用MORPH［21］和FG⁃NET［22］数据集作为测试集。MORPH 数据集包含14~77 岁年龄段的13 647 名不同种族的55 174 张图像，并且其中超过90% 的图像是非洲或欧洲人。FG⁃NET 数据集包含1 002 张来自82 个人的图像，年龄范围是0~70 岁，其中的面部图像在姿势、表情和光照条件等方面皆存在巨大差异，因此FG⁃NET 更为符合实际场景当中的面部图像。

2.3 实验设置及数据集预处理

本文采用预训练后的VGG 模型［23］作为主干网络进行年龄估算。最后的全连接层2 048 被替换为K，其中K为年龄级数且在本文中设置为101；CNN 网络的输入是224 像素×224 像素大小的面部图像；使用mini⁃batch 为80 的随机梯度下降算法对整体参数进行优化；动量和权重衰减系数分别设置为0.9 和0.000 5；卷积层、前2 个全连接层和最后1 个全连接层的学习率分别初始化为0.001、0.001 和0.01；在每轮中学习率都采用指数下降的模式；采用随机翻转、裁剪和颜色抖动进行数据增强。

训练集和测试集的每张图像都通过以下两个步骤进行预处理：（1）采用MTCNN 面部检测器［20］用于检测每个图像中的5 个面部标志（眼睛的左右中心、鼻尖、左右角）；（2）通过文献［24］中提出的方法，使用面部关键点来使每个面部居中并对齐；（3）将标准化后的脸部调整为256 像素×256 像素。在测试时，对估计到的年龄分布p中通过ŷ= argmaxk pk计算来获得预测年龄。

2.4 评估协议

2.4.1 同构数据集评估协议

本文采用了随机分割协议和S1⁃S2⁃S3交叉验证协议来评估MORPH 数据集上的年龄估算性能。MORPH 数据集中的图像在性别与种族中的分布非常不平衡，其中男女比例约为5.5，白人与黑人的比例约为4。借鉴文献［25⁃29］，将MORPH 数据集分为3 个不重叠的子集S1、S2和S3，以缓解这种不平衡分布。这种划分方式使男女比例约为3，而白人与黑人比例约为1。由此进行了两个实验：（1）使用S1进行训练，使用S2+S3进行测试；（2）使用S2进行训练，使用S1+S3进行测试。本文实验也使用上述2 个协议及其平均值评价性能，将这2 个协议分别定义为S1/S2+S3协议和S2/S1+S3协议。

2.4.2 异构数据集评估协议

现有的年龄估算方法主要遵循同构数据集评估协议，即训练和测试集来自同一数据集。例如在随机分割协议中，随机选择数据集的80% 图像进行训练，其余的用于测试。使用同构数据集评估协议而训练的模型可能会对训练集具有有偏性，并在面对未知信息的面部图像时会提供不可靠的年龄结果。在许多实际场景中，测试和训练集中的分布和特征完全不同。因此，同构数据集评估协议在评估年龄估算方法的泛化性能方面始终具有局限性。

本文提出了一种新颖的年龄估算评估协议，称为异构数据集评估协议（图3），它使得年龄估算方法的性能评价更有意义。该协议主要考虑的是训练后的模型应完全不了解测试数据集的分布及特征，这意味着不应使用测试数据集中的任何图像来训练网络。此外，训练集和测试集也不应该使用同一个人的不同条件下的面部图像。这便是与同构数据集协议的不同之处，在同构数据集协议中，测试图像与训练图像来源于同一数据集。在本文的评估协议下，可以更可靠地评估训练模型的泛化能力。

图3 两种数据集层面的评估协议对比Fig.3 Comparison of different assessment protocols

2.5 结果分析

2.5.1 超参数对性能的影响

本文提出的损失函数中唯一的超参数是α，因此本节评估其对年龄估算性能的影响。将α值从0.1更改为1，并使用VGG 模型在IMDB⁃WIKI 数据集中训练，然后在FG⁃NET 数据集中进行验证，得到的不同α值情况下的MAE，如图4 所示。图4 结果表明，当0.4 ≤α≤0.55 时，α值对年龄估算的结果影响较小；当使用较大或较小的α值时，年龄估算的性能会降低。 基于此分析，本文将α的值固定设置为0.5。

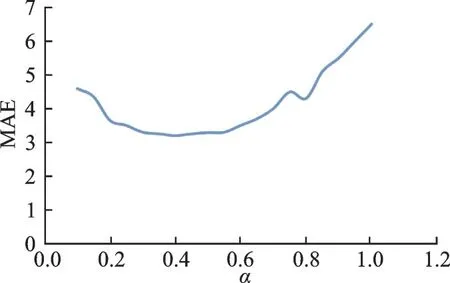
图4 不同超参数对MAE 的影响Fig.4 Performance difference among differ⁃ent hyperparameters

2.5.2 采用同构数据集评估协议的实验对比

本节在同构数据集评估协议下对本文年龄估算方法的性能与其他方法进行比较。随机分割、S1/S2+S3和S2/S1+S3协议下的MAE 值和CS 分值如表1、2 所示。

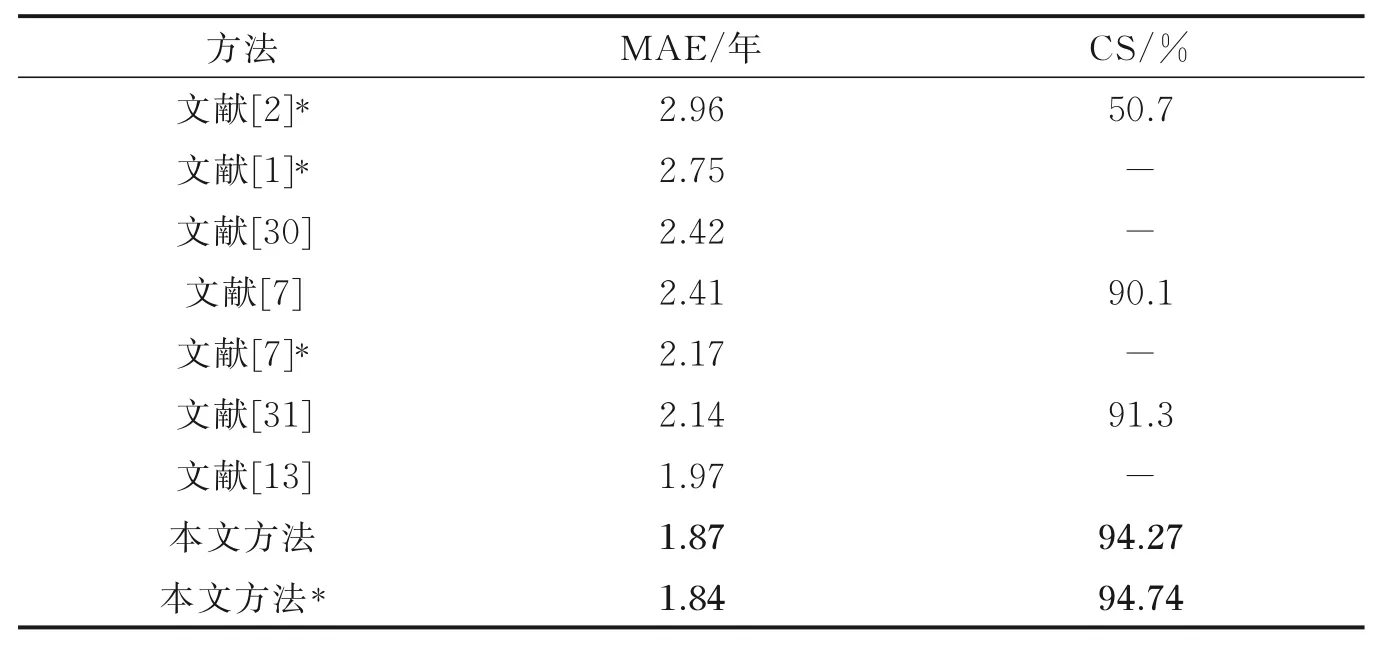
表1 MORPH 中采用随机分割协议的性能对比Table 1 Performance comparison under random splitting protocol in MPORH

表1 中文献［2］将年龄估算分类问题转换为排序问题进行解决；文献［1］提出一种紧凑型级联的基于上下文的年龄估算模型；文献［30］使用带有标签分布编码的KL 和KL⁃M 损失函数；文献［7］采用CE⁃MV 作为损失函数，并采用one⁃hot年龄标签编码；文献［31］提出可微的深度随机森林；文献［13］采用基于标签分布的年龄估算方法。从表1 中可以看出，本文方法在MORPH 数据集上的随机分割协议下达到了最优的性能。当直接在MORPH 数据集上对模型进行微调时（此时没有在IMDB⁃WIKI 数据集上对网络进行预训练），MAE 值可以达到1.87。为了进一步提高性能，在IMDB⁃WIKI 数据集上对网络进行了预训练，可以看出，本文方法得到的MAE 为1.84，这相比于其他方法中的最优方法提高了0.13年。

表2 中文献［27］采用基于“结构”的年龄估算方法；文献［32］进行年龄差异的估算；文献［33］引入辅助人口统计信息进行年龄估算；文献［34］先采用相关的属性对年龄进行分类，继而采用排序方法进行年龄估算；文献［28］采用组编码与解码进行年龄估算；文献［35］采用软排序对标签进行建模。根据表2结果可以看出，本文方法无需在任何其他年龄相关的面部数据集上进行预训练即可实现2.8 的平均MAE。与其他方法中最优的结果相比，CS 分值提高了0.18%。 同样地，在采用IMDB⁃WIKI 数据集进行预训练后进一步提高了性能：MAE 为2.73，CS 为86.42%。从表2 中还可以看出，其他方法在S1/S2+S3和S2/S1+S3协议下的结果之间存在明显差距，证实了现有方法对训练数据集的特征与分布变化（如性别，肤色等）较为敏感，而本文方法在两种协议上的性能相差无几。值得一提的是，文献［34］通过采用多任务学习策略来提高训练模型对性别、种族等不同面部属性特征的鲁棒性，从而达到与本文方法相似的性能。然而，本文方法是在没有利用其他属性（例如性别和肤色等）的基础上提高了训练模型的鲁棒性。

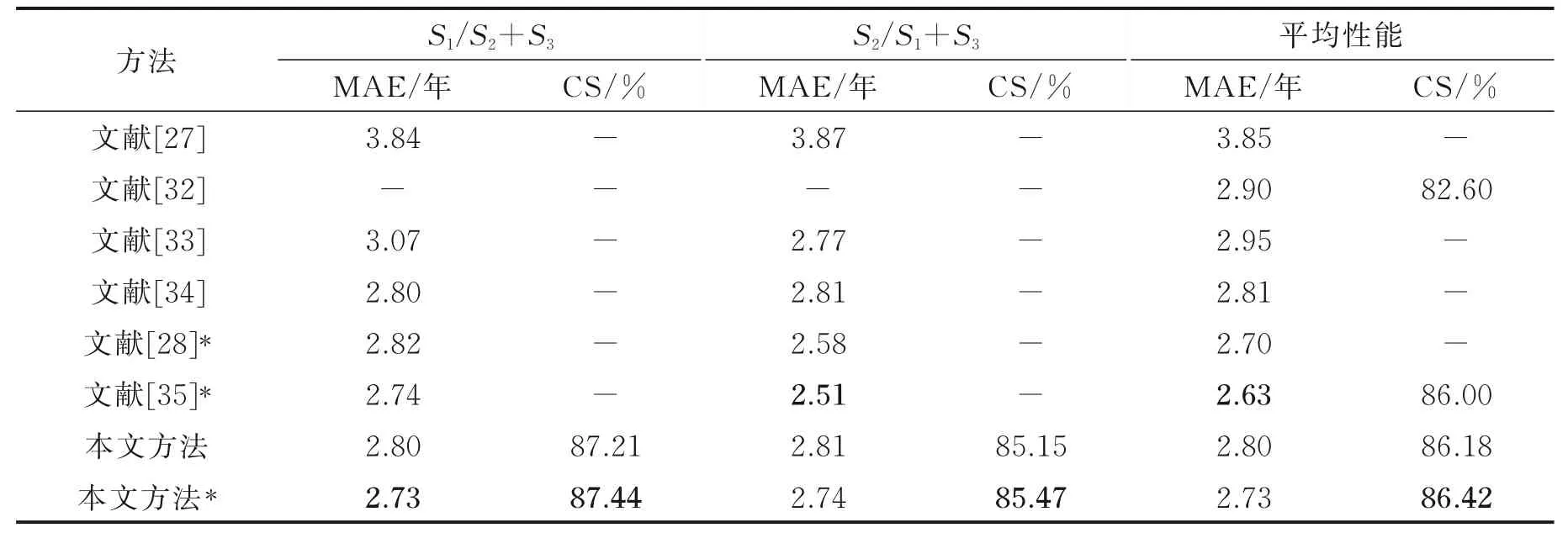
表2 MORPH 中采用S1/S2+S3和S2/S1+S3协议的性能对比Table 2 Performance comparison under S1/S2+S3 and S2/S1+S3 protocols in MPORH

在同构数据集评估协议下仿真的常见问题是测试到的结果带有有偏性，而这种有偏性在S1/S2+S3和S2/S1+S3评估协议下体现得更加淋漓尽致。因此在该协议下，无法衡量年龄估算方法在对未知面部图像的泛化能力。

2.5.3 采用异构数据集评估协议的实验对比

考虑到在同构数据集评估协议下可能无法准确度量年龄估算方法的性能，本节在本文提出的异构数据集评估协议中进行了更为有效的实验。为了公平地进行比较，本文在IMDB⁃WIKI 数据集训练了这些模型，此外还用JS 对称损失函数和χ2⁃统计量训练VGG 模型以表明所提出的损失函数的有效性。采用异构模型在不同目标域的性能对比如表3、4 所示。

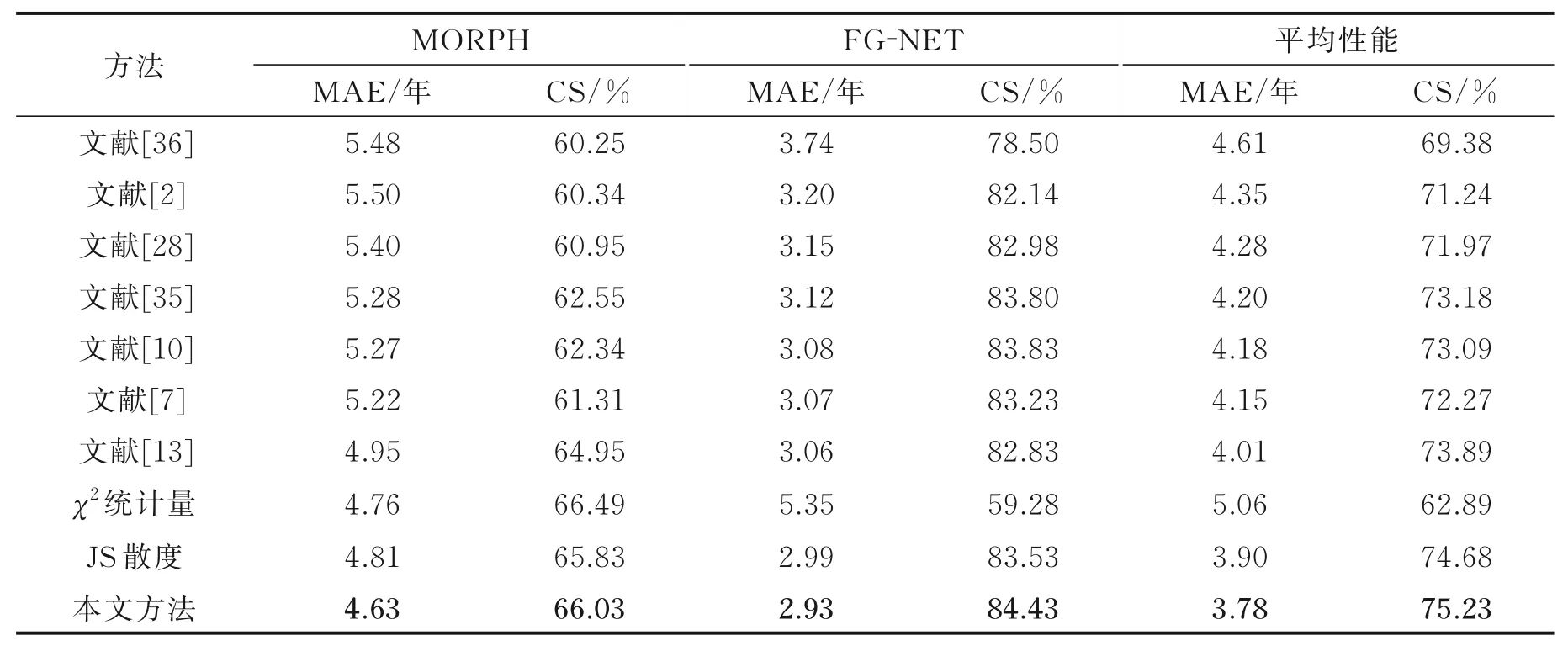
表3 采用异构数据集评估协议在不同目标域中的性能对比（训练集：IMDB‑WIKI）Table 3 Performance comparison under proposed protocol and different testing sets （training set：IM‑DB‑WIKI）

表3 中文献［36］使用排序CNN 进行年龄估算；文献［10］提出带有标签歧义性的深度标签分布方法；文献［28］进行人口统计方面的统计。从表3、4 结果可以看出：

（1）文献［10］和文献［13］方法的年龄估计准确性高于文献［2］和文献［7］（CE⁃MV）方法，这表明标签分布有助于改善年龄估算的性能。这是因为在训练过程中，基于one⁃hot 编码方式的损失函数并未考虑标签模糊性（ambiguity）的影响［10］。

（2）文献［35］的MAE 和CS 与文献［18］方法比较接近，这是因为文献［35］和文献［10］的算法具有线性关系［13］。应当强调的是，诸如CE⁃MV 和文献［13］之类的方法分别在CE 和KL 损失函数中加入了正则项，正是由于这些正则化参数的大小不同，导致训练网络的最终对正则化参数的选择相当敏感。与之不同，本文提出的损失函数没有任何正则化超参数，因此可以有效地缓解此问题，从而在年龄预测时保持良好的性能。

表4 采用异构数据集评估协议在不同目标域中的性能对比（训练集：IMDB‑WIKI‑40k）Table 4 Performance comparison under proposed protocol and different testing sets （training set：IM‑DB‑WIKI‑40k）

（3）从表3 的下半部分可以推断出，采用本文DC 损失函数进行年龄估算时的准确性显著高于其他对称损失函数（例如χ2统计量和JS 散度）所获得的预测准确性，这些结果也为第1 节中的理论分析增加了实验支撑。因此可以得出，本文的方法在异构数据集测试中具有良好的泛化能力，因此可以处理未知场景。

本文还进一步使用MORPH 数据集对模型进行训练以对异构数据集评估协议进行进一步效果分析，结果如表5 所示。可以看出，采用MORPH作为训练数据集时，所有方法的性能都会下降，但本文方法仍然是性能最好的方法。

表5 采用异构数据集评估协议在FG‑NET 中的性能对比（训练集：MORPH）Table 5 Performance comparison under proposed protocol and FG‑NET （training set：MORPH）

当比较同构数据集评估协议（表1、2）和异构数据集评估协议（表3、4）在MORPH 上的实验结果时，发现在同构数据集评估协议下达到较高的年龄估算准确性并不能保证在面对未知目标域时仍具有良好的性能。很显然，未知情况会导致所有年龄估算方法的性能下降，这可能因为它们并没有学习到在不同性别、不同光线变化、不同姿势和不同面部表情变化的不同特征与分布的图像特征。但是，无论在哪种评估协议中，本文方法仍然得到最优的MAE 和最高的CS，这也进一步说明了本文方法的有效性和鲁棒性。

3 结束语

本文考虑年龄的标签值通常呈现局部相关性，将年龄估算问题建模为一个以真实年龄值为中心的高斯分布学习问题。为了使得模型参数学习到这种分布特征，提出了一个损失函数用于提供估计分布与真实分布之间的迭代逼近。然后，为了更好地评估年龄估算方法的泛化性能，与此前通常假设训练集与测试集中数据同特征同分布的同构数据集评估协议不同，提出了更符合年龄估算方法的实际用例场景的异构数据集评估协议。理论分析和实验结果皆证明了本文方法的有效性。