一种基于多尺度特征和改进采样策略的异构网络对齐方法

任尊晓，王 莉

（太原理工大学大数据学院，晋中 030600）

引 言

信息技术的快速发展提供了越来越多的服务平台，用户会在不同平台上使用不同的服务内容，产生了不同的数据信息。多平台数据融通将会为提升服务质量提供有利支撑。融合异构网络的首要问题是如何对齐不同平台的对象，即异构网络对齐问题［1］。

实际应用中，异构网络对齐往往首先选择节点的属性信息作为匹配依据。例如，社交网络平台或电商平台中，节点属性特征一般包括用户名、性别、地域、签名爱好等属性信息。早期的网络对齐研究中，一些研究者以用户名为出发点，从词汇的角度对其进行分析［2］，或将从不同网络获取的用户名和用户简介抽取出来，采用Jaccard 相似度等方法计算文本字段的相似性来匹配用户身份［3‑6］。这类方法直观简单，但是出于隐私保护［7］等考虑，用户名及一些自报道信息经常缺失或具有伪装、虚假等性质，误导判断。因此，这种依靠节点属性特征的方法对异构网络对齐问题解决有局限性。

节点间的关系结构提供了节点对齐的新特征［8］。社交平台上用户间的行为关系往往是用户真实意图的反映，这种结构信息为异构网络对齐提供了较为可信的计算依据。文献［9‑11］通过统计共享的好友数来计算节点之间的匹配度。有研究通过分析节点的公共邻居集、Jaccard 系数等［12］邻居特征来对齐节点，有利弥补了基于节点属性特征的异构网络对齐的不足。但是，这类方法面临一个严重挑战，即网络结构对噪声和结构变化非常敏感，当网络结构发生细微变化时，节点对齐的性能往往会下降。

近年来，网络表示学习的研究为表达网络结构的规则性带来了新思路。网络表示学习就是在保持原有网络结构特征的基础上，将网络映射到一个低维密集向量空间，同时降低节点表示对噪声和网络结构变化的敏感性［6，9，13］。基于网络表示学习的网络对齐模型可分为有监督模型和无监督模型。监督模型通常以锚节点（即事先已知的匹配节点集）为线索，建立机器学习模型得到节点表征。然而，事先已知的锚节点数量往往非常少，甚至几乎没有。近年来，一些无监督的方法被提出，在没有任何先验知识的情况下建立网络节点的表达，主要有两种路线，基于机器学习的策略和基于矩阵分解的策略。在基于机器学习策略中，有研究提出了一种多级图卷积框架，为了处理大规模的网络，设计了一种空间协调机制，在基于网络划分的并行训练和跨不同社交网络的账户匹配中对表征空间进行对齐［14］。有研究在全局结构上利用节点的邻居信息表示节点［15］，将节点向量映射到低维空间中，学习节点的潜在表示［16‑17］。基于矩阵分解的方法利用矩阵分解得到节点表示，避免了随机游走带来的偏差和计算开销大的问题。2018年，Heimann 等［15］提出了一种基于矩阵分解的模型REGAL，首先建立网络结构和属性结合的节点相似度矩阵，然后采用随机抽样策略，选取少量地标节点与所有节点建立关联，以此来学习所有节点的表示。在多个数据集上的实验表明了此模型的优越性，但是，其特征设定的局限性和随机抽样策略所选取地标节点的代表性在一定程度上影响了算法性能。

本文针对REGAL 模型进行了改进，提出一种多尺度特征抽取和采样策略改进的异构网络对齐的无监督模型。首先，提出一种不同尺度的节点特征表示，提取节点特征；然后利用node2vec［18］模型获得网络表征，在此基础上，设计了一种基于节点重要性的地标节点采样策略选择最重要的地标节点，改进随机抽样策略；引入一种低秩矩阵近似方法进行矩阵分解，学习节点的表示；最后，根据节点表示的相似性对网络进行对齐。主要贡献如下：

（1）提出一种包含节点聚类系数、邻居平均度和高阶邻居度的多尺度的网络节点特征表示，增强节点表达，这3 个特征代表了节点在不同尺度下的结构特性；

（2）提出一种基于节点结构信息和重要程度的改进的地标节点采样策略；

（3）在多个不同领域、规模和稀疏度的数据集上进行实验，结果表明本方法优于其他基线算法。

1 相关工作

根据与本文技术的相关程度，主要对基于网络表示的异构网络对齐方法的相关工作进行阐述。

基于网络表示的方法的基本思想是将网络中的节点映射到低维、稠密的向量空间中，达到同时保持网络结构规则性和降维的目标，以此进行网络对齐。通常，利用网络表示方法学习到的表征能够保持原始网络结构的特性，例如一阶接近性和二阶接近性［19］。一阶接近性是指节点与它的一阶近邻之间的拓扑关系。在二阶接近性中，每个节点扮演两个角色，即节点本身和它作为其他节点的“上下文”角色。Yang 等［20］提出将顶点的文本特征引入到网络表示学习中学习节点的潜在表征。Tan 等［6］将网络映射到超图上对高阶关系进行建模，学习节点的潜在特征。Liu 等［13］利用网络表示技术学习每个用户作为关注者与被关注者的上下文特征，同时使用种子用户对作为约束条件，去对齐未知身份的用户对。Tong 等［21］利用网络表示技术将原始网络映射到一个低维的向量空间中，使用锚链的信息学习一个稳定的跨网络映射来进行锚链预测。这些研究重点关注了节点在局部结构上的特性，忽略了节点在全局结构中的信息。因此，一些研究从多结构出发，探索节点的结构特征。Grover 等［18］提出一种网络节点表示方法node2vec，建立了一种兼顾深度和广度随机游走策略的节点嵌入方法，提高了网络表示效果。Fu 等［16］考虑到节点的局部和全局信息，提出一种多粒度用户身份对齐框架。这些方法均在异构网络对齐上取得了不错的效果，但计算效率低。考虑到这一问题，有研究采用矩阵分解方法推导节点的表征，而不必通过复杂的训练过程。通常，基于矩阵分解的网络表示学习模型包含两个步骤：（1）构建一个表示节点之间关联关系的矩阵，这个矩阵可以是表达节点间拓扑关系的邻接矩阵，也可以是表示节点之间相似性的相似度矩阵；（2）在构建的矩阵上进行矩阵分解，得到节点的潜在表征。基于这一思想，Heimann 等［15］提出一种基于隐矩阵分解的网络对齐方法，采用低秩矩阵近似法改进矩阵分解策略。首先建立一个结合属性信息和全局结构信息的节点相似度矩阵，然后通过随机抽样策略选取地标节点，利用少量地标节点与所有节点建立关联，再利用矩阵分解推导出节点表示，降低了计算复杂度。但是，地标节点的选取对低秩矩阵近似非常重要，其随机选取地标节点的策略使得计算结果准确度无法得到保证。

2 一种无监督的网络对齐模型MU3S

问题定义 已知两个无权无向图G1(V1，E1)和G2(V2，E2)，其中V1和V2分别表示两图中的节点集，E1和E2分别表示两图中的边集。V=V1∪V2，E=E1∪E2分别表示合并后的网络G的节点集和边集。异构网络对齐问题为推导出一个对齐矩阵simemb，其中simemb(u，v) 表示节点u∈V1和v∈V2之间的相似性。

本文提出一种基于多尺度特征和改进采样策略的异构网络对齐方法（Aligning heterogeneous net‑works by MUlti‑scale features and improved sampling strategies，MU3S），通过设计不同尺度的节点结构特征和基于节点重要性的地标节点采样策略来提高异构网络对齐能力。该模型主要分为网络合并、多尺度特征提取、地标节点采样、相似矩阵构建、网络表示生成和异构网络对齐6 部分，框图如图1 所示。

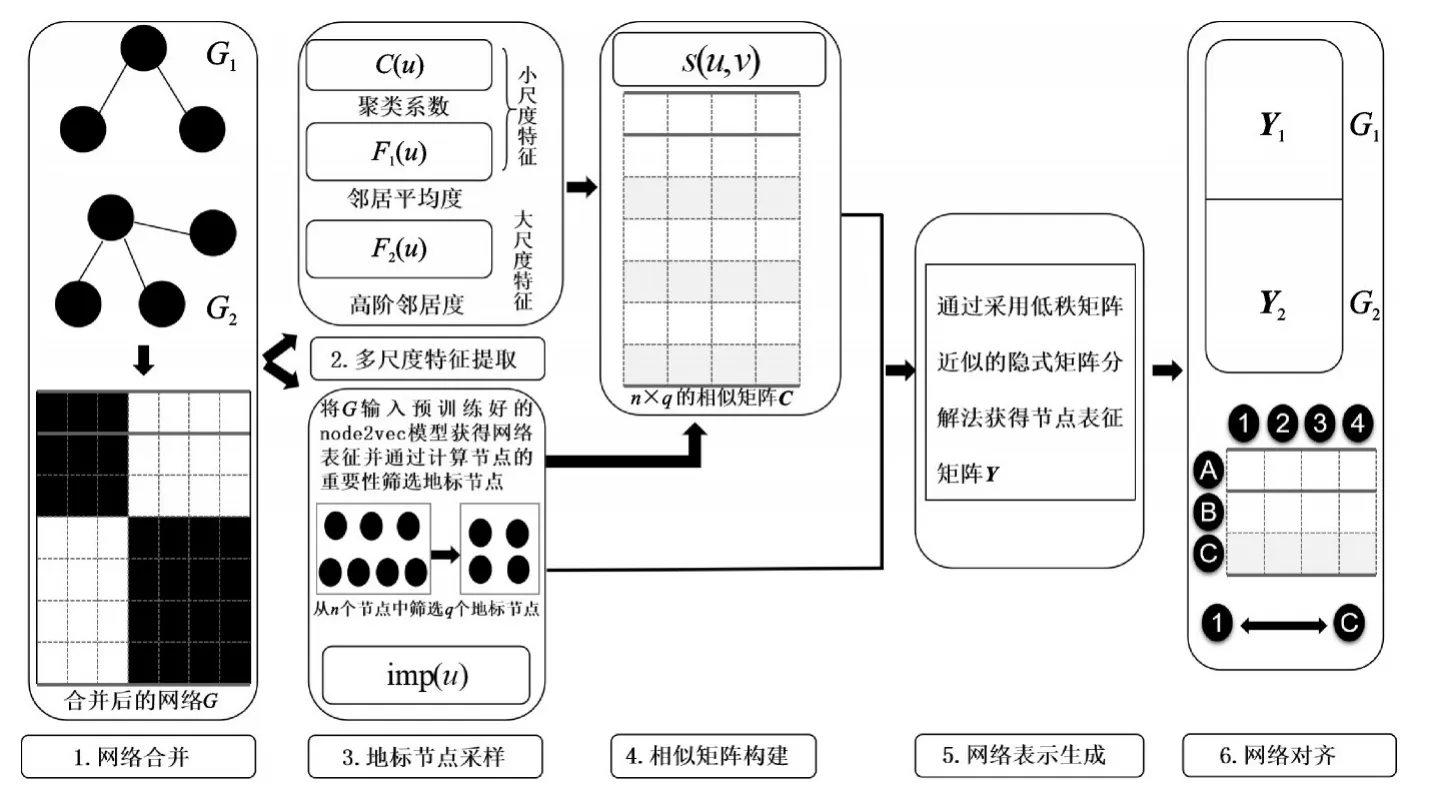
图1 MU3S 的概述Fig.1 Overview of MU3S

2.1 网络合并

首先，将待对齐的两个网络合并为一个图G，表示为邻接矩阵A。然后基于此邻接矩阵进行后续计算。 合并的方式为将分别具有邻接矩阵A1和A2的图组合成一个块对角邻接矩阵，组合方式为[A10；0A2]，其中A1和A2分别表示G1和G2的邻接矩阵。

2.2 多尺度结构特征提取

本文从节点的局部结构和全局结构两种尺度出发，提出3 种结构度量指标作为节点的结构特征。

（1）聚类系数

网络中的相似节点往往会与周围邻居建立相似的亲密关系，表现为节点与周围邻居的聚集程度。因此，建立了节点聚类系数C(u)作为节点的一种局部特征，即

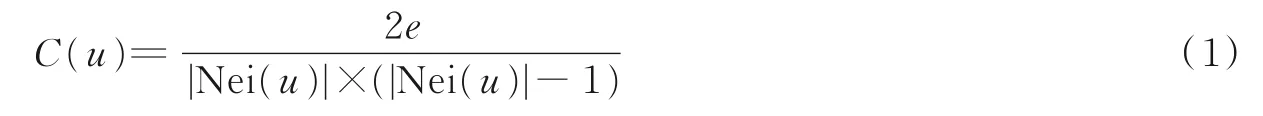
式中：Nei(u)表示节点u的一阶邻居集合，e表示Nei(u)构成的网络中边的数量。（2）邻居平均度

节点的邻居平均度表达了节点周围邻居的分布。由于节点邻居的度值可能差别很大，进行归一化以消除度差异产生的影响，其计算公式为

（3）高阶邻居度

本文建立了高阶邻居度以提取邻居节点在全局结构中的特征，其计算方法为

在所构建的3 个特征中，聚类系数和邻居平均度是针对节点局部特征的表示，称之为小尺度特征；高阶邻居度计量了节点的全局信息，称之为大尺度特征。将此3 个特征进行拼接，得到所有节点的初始特征表示R(u)，R(u)=(F1(u)，F2(u)，C(u))。

2.3 地标节点采样

为了降低计算复杂度，本文对节点建立基于地标节点的表达。地标节点是能够表现出网络结构不同特征维度的标准节点，地标节点选择不同，节点表征效果也不同。REGAL 模型采用随机策略选择地标节点。为了更好地获得具有重要信息表达的节点表征，本文设计了一种基于节点嵌入和重要性的地标节点选择策略。首先，引入node2vec 方法［18］得到图G的节点嵌入表示；然后，基于所设计的计算节点重要性的方法选取地标节点。节点u的重要性评估计算方法为

式中：AG为通过node2vec 模型得到的网络表征矩阵，表示节点u在向量空间中的大小。对所有节点按照重要性大小进行排序，选取排名前q的节点作为地标节点。通常，其中t为采样系数。

2.4 相似矩阵构建

通过基于节点重要性的采样策略筛选出地标节点后，利用相似函数s(u，v)计算节点间的相似性，用于比较图内或图间的节点。计算方法为

式中R(u)表示节点u的初始特征。通过计算，得到一个由G1和G2中节点之间的相似性组成的相似矩阵S。

2.5 网络表示生成

本文借鉴相关文献［15］，引入一种隐式矩阵分解方法进行网络表示。利用相似矩阵S，找到矩阵Y和Z，使其满足S≈YZT，其中Y是所求的节点表征矩阵。基于低秩矩阵近似方法，通过一个低秩矩阵近似表示相似矩阵S。的计算式为

式中：C为G中所有节点与q个地标节点相比较得到的相似矩阵；W为从C中提取的q×q维的包含地标节点间相似性的子矩阵，W+是它的逆矩阵。文献［15］已经表明，C与W+以及CT的乘积足以逼近相似矩阵S，并可以在不对因式分解的情况下获得节点表征矩阵Y。

根据式（6），在子矩阵W+上执行奇异值分解，可得

式中U和Σ是对W+执行奇异值分解得到的两个子矩阵。

上述方法在求解节点表征矩阵Y的过程中不需要计算完全相似矩阵S，只需计算所有节点与q个地标节点之间的相似性，形成相似矩阵C，然后对子矩阵W+进行奇异值分解即可。这种结合低秩矩阵近似的矩阵分解方法降低了计算复杂度，最终可获得网络节点表征矩阵的近似矩阵。

2.6 网络对齐

根据G1和G2的维度大小，将网络表征近似矩阵划分为，得到G1和G2各自对应的节点表征矩阵。然后，使用欧几里得距离计算节点表征之间的相似性构建对齐矩阵，匹配两个网络中的节点。计算方法为和

通过计算，得到相似度值。对于每个节点，选择相似度最高的节点作为其对齐节点。

3 实验设计与结果分析

3.1 数据集和准备工作

本文选取了社交网络、生物医学和论文库3 种不同领域的数据集进行实验。

（1）Arenas Email［15］：是一个社交网络公共数据集，包含许多Email 信息。该数据集的规模较小，每条数据表示两个用户通过电子邮件进行通信所产生的关联关系。

（2）PPI［15］：是描述蛋白质之间相互作用的数据集。该数据集的规模中等，每条数据表示蛋白质与蛋白质之间相互作用关系。

（3）Arxiv［15］：一个收集了物理学、数学、计算机科学与生物学论文预印本的数据集。该数据集规模较大。借鉴相关文献［15］的数据集处理方法，对每个真实网络G1，利用它的邻接矩阵A1，根据公式A2=PA1PT生成一个具有邻接矩阵A2的新网络G2，其中P为随机生成的置换矩阵。在不断开任何节点的情况下以0.01 的概率去掉网络G2中的边，将结构噪音随机添加到G2中。最后，将邻接矩阵A1和A2以块对角矩阵的形式合并，作为模型的输入。 Arenas Email‑2、PPI‑2、Arxiv‑2 都是通过 这种方式从Arenas Email‑1、PPI‑1、Arxiv‑1构建而来。数据集统计信息如表1 所示。

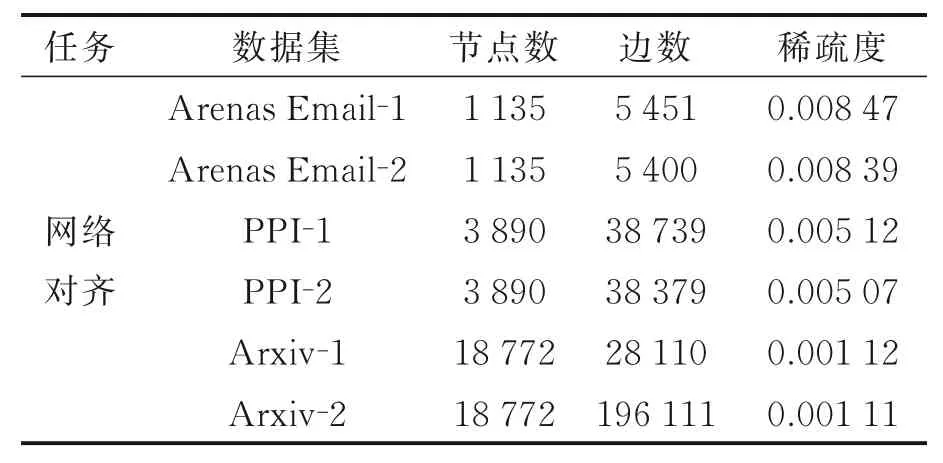
表1 数据集统计信息Table 1 Statistics of datasets

3.2 基线模型

为了验证MU3S 模型的有效性，将其与5 种基线模型进行对比，其中包括3 种无监督网络对齐模型和两种MU3S 模型的变体。

（1）IsoRank［22］：该模型对不同的物种关系建模构建生物网络，然后利用相似性得分将两个网络中可能具有关联关系的节点进行匹配，最后通过提取一组得分高、相互一致的匹配来构建网络对齐的映射。

（2）FINAL［23］：该模型的思想是利用节点或边的属性信息来指导对齐过程，从最优化角度，提出了一种基于对齐一致性原则的最优化公式解决属性网络的节点对齐问题。

（3）REGAL［15］：该模型是一种基于网络表征的图对齐模型，它利用了表征学习的强大功能来匹配不同图中的节点。其中，REGAL 模型设计了一个可移植的算法xNetMF 学习节点的潜在表征。

（4）MU3S‑sample：它是本文模型MU3S 的一个变体，去除了不同尺度节点特征的改进，只保留了基于节点重要性的采样策略的改进。

（5）MU3S‑feature：它是本文模型MU3S 的另一个变体，去除了节点采样策略的改进，只保留了多尺度特征的改进。

3.3 评价指标

从两种不同角度采用3 个评价指标对模型进行评测。从预测的角度，采用准确率和Top‑k准确率两种指标对模型进行评估；从排序的角度采用MRR 对模型进行评估。

（1）准确率

准确率是一个非常直观的评价指标，准确率越高，则表示网络对齐算法的性能越好。在网络对齐问题中，准确率被定义为预测正确的对齐节点对数除以真实对齐的节点对数，计算公式为

式中：count 表示模型预测正确的对齐节点对数，Gt表示真实对齐的节点对数。

（2）Top‑k准确率

准确率Accuracy 属于硬对齐，它要求节点之间的对齐是一对一的关系。为了不失一般性，本文还采用了软对齐Top‑k准确率。Top‑k准确率表示与节点对齐的候选节点存在于前k个候选节点列表中。对于G1中的每一个节点，计算它与G2中任意节点间的相似性，并按照降序的方式依次排列，将排名前k的节点存储在潜在匹配列表中。然后将潜在匹配列表的节点的索引依次与真实对齐节点对中的编号比较，只要有一个命中，就认为匹配成功，具体的计算过程为

需要注意的是，这种度量方法不适用于只寻找硬对齐的基线模型FINAL 和IsoRank。

（3）MRR

MRR 是推荐算法中常用的一种评估指标，其含义是把标准答案在被评价系统给出的结果中的排序取倒数作为它的准确度，再对所有的问题取平均。现将MRR 指标应用于异构网络对齐问题中，从排序的角度对模型的对齐质量做出评估，计算公式为

式中ranki为第i个节点在经过排序后的对齐列表中的索引值，取其倒数作为该节点获得的排序分数。

3.4 超参设置

模型中涉及3 个重要超参，K，t和α，根据多次实验后的效果和相关基线论文参数设置情况对超参进行了设定。

参数K表示邻居的跳距，在不同数据集上进行实验，结果如图2 所示。可以看出，随着K值的增加，高阶邻域对节点表示能力减弱。多次重复实验显示出，K值为2 时，模型的准确率最高，因此本模型中K设定为2。

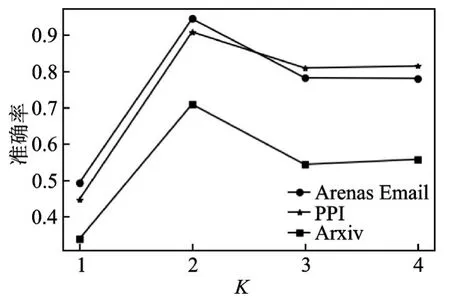
图2 超参K 分析Fig.2 Analysis of hyper‑parameter K

参数t表示地标节点的采样系数，它控制着地标节点的数量。实验结果如图3 所示，随着采样节点数量的增加，模型的性能逐渐提高。考虑到计算量的大小，t最终被设定为10。其中，地标节点的数量为，MU3S 对地标节点个数的设定与基模型REGAL 一致。

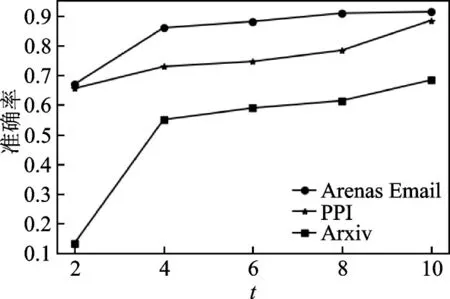
图3 超参t 分析Fig.3 Analysis of hyper‑parameter t

超参数α表示折扣系数，代表节点不同阶邻居的重要性，实验结果如图4 所示。对于Arenas Email 和PPI 两个数据集，模型的准确率在α设置为0.01 时最高，而在Arxiv 中，α设置为0.005 时准确率最高。由于Arxiv 中α设置为0.005 和0.01 的结果差异不大，因此，将超参数α统一设定为0.01。

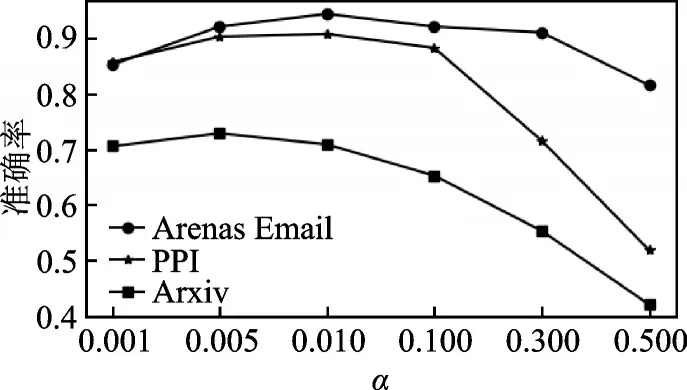
图4 超参α 分析Fig.4 Analysis of hyper‑parameter α

3.5 实验结果分析

表2~4 的实验结果表明，在3 种实验指标的衡量下，MU3S 与基线模型相比性能均为最优。两个变体模型的实验结果进一步表明了多尺度特征抽取与基于节点重要性的采样策略的有效性。

（1）网络表示方法的有效性：从表2~4 的实验结果可看出，4 种基于网络表征的方法（RE‑GAL，MU3S，MU3S‑sample，MU3S‑feature）的性能均优于没有使用网络表征的FINAL 和IsoRank。这一结果表明，基于网络表征的模型学习到的节点表征具有更强的表现力，能够更好地完成网络对齐任务。

表2 基线和MU3S 的准确率Table 2 Accuracy of baseline and MU3S

（2）多尺度特征的有效性：MU3S 算法是在REGAL 算法的基础上改进而来的。在保留REGAL 全局结构特征的情况下，设计了聚类系数和邻居平均度两个特征，丰富了节点在局部结构上的表达。从表2~4 的实验结果可观察到MU3S‑feature 比REGAL 的表现更好，验证了多尺度特征的构建对异构网络对齐任务的有效性。

（3）采样策略的有效性：MU3S‑sample 首先将网络输入一个预训练好的node2vec 模型中获得网络表示。node2vec 采用了一种灵活的邻域抽样策略，经过深度优先和广度优先的随机游走生成节点序列，使得到的节点表征蕴含了结构信息。在此基础上，设计了一种节点重要性评估计算方法，筛选出了蕴含着结构信息的排名前q的地标节点。从表2~4 可以看出，MU3S‑sample 的性能优于REGAL，验证了本文提出的采样策略的有效性。

表3 基线和MU3S 的Top‑k accuracy 值Table 3 Top‑k accuracy of baseline and MU3S

（4）结合多尺度特征和改进的采样策略的有效性：表2~4 的实验结果表明，MU3S 在3 个数据集上均取得了最佳性能。这一结果表明，多尺度特征的提取结合基于节点重要性的采样策略能够优化模型，使学习到的节点表征更准确，在异构网络对齐任务中表现更好。

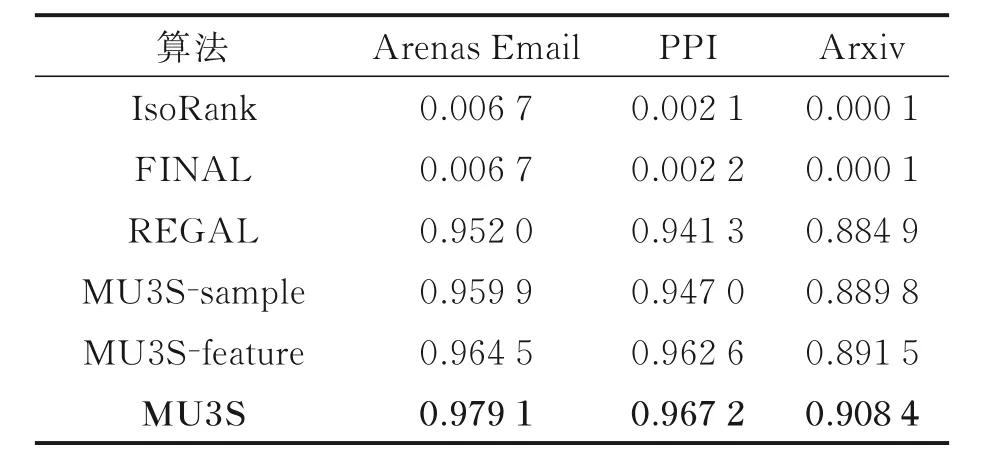
表4 基线和MU3S 的MRR 值Table 4 MRR of baseline and MU3S

（5）模型的时间复杂度分析：假设两个网络均有n个节点，对MU3S 的时间复杂度展开分析。在多尺度特征提取阶段，计算聚集系数的时间复杂度为O(n)，邻居平均度的时间复杂度为O(n2)，高阶邻居度的时间复杂度为O(n3)，这一步的总时间复杂度为O(n6)。 筛选地标节点所需的时间复杂度为O(nq)。 计算相似度矩阵的时间复杂度为O(nqb)。利用矩阵分解方法获得节点表征的时间复杂度为O(nq2)。对齐两个网络中对应节点的时间复杂度为O(n2)。与基模型REGAL 相比，MU3S 在特征提取阶段和筛选地标节点阶段增加了时间复杂度，但获得了更高的准确率。

4 结束语

本文提出了一种无监督的网络对齐模型MU3S，首先从不同尺度提取节点的结构特征，设计了一种基于节点重要性的采样策略选择地标节点，建立了基于地标节点的相似关系矩阵，利用低秩矩阵近似方法进行矩阵分解，得到节点表示，最后通过计算节点表示之间的相似性对齐网络。在3 个不同领域的数据集上进行实验，实验结果表明，MU3S 模型在网络对齐任务中具有比基线方法更优的性能。

异构网络对齐是大数据研究领域中的一个重要问题，实际场景中，数据噪音、数据规模大等均使得该问题极为复杂，下一步将在网络表示模型上和计算效率方面进行更为深入的研究。